Mixed-dimensional multi-scale poroelastic modeling of adipose tissue for subcutaneous injection

Abstract

Subcutaneous injection of therapeutic monoclonal antibodies (mAbs) has gained increasing interest in the pharmaceutical industry. The transport, distribution and absorption of mAbs in the skin after injection are not yet well-understood. Experiments have shown that fibrous septa form preferential channels for fluid flow in the tissue. The majority of mAbs can only be absorbed through lymphatics which follow closely the septa network. Therefore, studying drug transport in the septa network is vital to the understanding of drug absorption. In this work, we present a mixed-dimensional multi-scale (MDMS) poroelastic model of adipose tissue for subcutaneous injection. More specifically, we model the fibrous septa as reduced-dimensional microscale interfaces embedded in the macroscale tissue matrix. The model is first verified by comparing numerical results against the full-dimensional model where fibrous septa are resolved using fine meshes. Then, we apply the MDMS model to study subcutaneous injection. It is found that the permeability ratio between the septa and matrix, volume capacity of the septa network, and concentration-dependent drug viscosity are important factors affecting the amount of drug entering the septa network which are paths to lymphatics. Our results show that septa play a critical role in the transport of mAbs in the subcutaneous tissue, and this role was previously overlooked.

1 Introduction

The treatment of many diseases (Lu et al. 2020), such as migranies (Tso and Goadsby 2017), cancers (Glassman and Balthasar 2014; Pivot et al. 2014), psoriasis (Burmester et al. 2013), and COVID-19 (Taylor et al. 2021), relies on effective delivery of therapeutic antibodies (mAbs). Subcutaneous delivery of mAbs has attracted increasing attention in the pharmaceutical and healthcare industries due to its increased patient compliance and convenience as well as reduced healthcare expenses (Haller 2007; Jackisch et al. 2014). However, compared to intravenous administration, further development of subcutaneous delivery is hindered by many challenges including low bioavalibility (Bittner et al. 2018; Porter et al. 2001) and limited deliverable volume (Jackisch et al. 2014; Shpilberg and Jackisch 2013). To overcome these challenges and to improve delivery strategies, the study of drug transport and distribution in the adipose tissue during and after administration becomes critical.

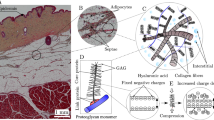
A histological image of porcine adipose tissue is shown in Fig. 1a. Adipose tissue consists of adipocytes, collagen fibers, blood and lymphatic capillaries (Comley and Fleck 2010). Lymphatic capillaries in the adipose tissue follow the fibrous septa (Klein 2000) which are bundles of collagen fibers (Comley and Fleck 2010). Due to their large molecular weight, mAbs are primarily absorbed by the lymphatic vessels and then enter the circulatory system (Hossain et al. 2013; Porter and Charman 2000; Supersaxo et al. 1990; Thomas and Balthasar 2019; Wang et al. 2012; Zhao et al. 2013). The convoluted route of mAbs entering the blood system is one of the reasons for their low bioavailability upon subcutaneous delivery. It is of high economic and scientific interest to study the transport and distribution of mAbs in adipose tissue after injection. Fibers are prelymphatic pathways for drug transport because their flow resistance is low (Ryan 1989; Skobe and Detmar 2000). As shown in Fig. 1b, septa form preferential channels for fluid flow (Thomsen et al. 2014). Therapeutic proteins (mAbs), entering the septa network, are in close contact with the lymphatics, thus are more likely to be absorbed before undergoing catabolism (Porter et al. 2001; Thomas and Balthasar 2019). As shown in Fig. 1a, there is a rich network of septa in adipose tissue. The diameter of septa bundles ranges from 30 $\upmu$m to 10 nm for porcine tissue (Comley and Fleck 2010), and the maximum thickness can be as large as several hundred microns in healthy non-cellulite human adipose tissue (Hexsel et al. 2009; Macchi et al. 2010; Wang et al. 2011). The contrast between the septa width and the characteristic length scales for tissue deformation and drug transport make this a multi-scale problem. Thus, we will consider septa as microscale features embedded in a macroscale tissue. The goal of this work is to model fluid flow and drug transport in the mascroscale tissue and along the microscale septa. We aim to study the volume fraction of injected drug entering the septa network in the adipose tissue.

Fig. 1

a Histological image of porcine adipose tissue. Adipocytes are shown in white. The septa are shown as magenta stripes. The scale bar is 1.5 mm. b Subcutaneous injection experiments, taken from Thomsen et al. (2014). (Left) Histological cross section. The drug has been dyed to appear red. (Right) X-ray CT scan of a similar injection. The volume shows the 3D shape of the drug plume. Preferential channels for fluid flow along septa are circled in red. The scale bar is 1 mm

Previous works (Leng et al. 2021a, b; de Lucio et al. 2020) have modeled the adipose tissue as porous media to study the mechanical response and pressure build-up in the tissue due to injection. It was found that solid deformation is important in predicting pressure distribution, and thus drug transport during subcutaneous injection. Drug transport coupled with solid deformation is also considered in Han et al. (2021) and Rahimi et al. (2022). However, these studies (Han et al. 2021; Leng et al. 2021a, b; de Lucio et al. 2020; Rahimi et al. 2022; Weickenmeier and Mazza 2019) are limited to the macroscale tissue matrix, and fail to consider the microscale fibrous septa. Fibers in soft materials have been well-studied, and their homogeneous contributions to macroscale solid deformation are studied in NíAnnaidh et al. (2012) and Sommer et al. (2013). In subcutaneous injection, the role of septa as preferential channels for fluid flow is similar to that of natural fractures in geophysical flows. Discrete fractures-matrix models are popular in modeling fluid flow in fractured porous media (Alboin et al. 2000; Angot et al. 2009; Faille et al. 2016; Flemisch et al. 2018; Frih et al. 2012; Froeschl 2003; Fumagalli and Scotti 2013; Martin et al. 2005; Odsæter et al. 2019; Schädle et al. 2019; Schwenck et al. 2015). The governing equations are averaged across the fractures, thus fractures can be represented as lower-dimensional interfaces embedded in the matrix. We borrow ideas from discrete fracture-matrix models and include the fibrous septa as interfaces in the adipose tissue matrix.

In this work, we present a mixed-dimensional multi-scale (MDMS) poroelastic model of the adipose tissue for subcutaneous injection. The macroscale tissue matrix is modeled as a deformable porous media. The fibrous septa are considered as reduced-dimensional microscale interfaces embedded in the tissue matrix. The solid deformation of the septa is homogeneous and characterized by the macroscale matrix. The fluid flow and drug transport along the septa are modeled explicitly. The model is first verified by comparing numerical results against the full two-dimensional (2D) model where fibrous septa are resolved using fine meshes. Then, we apply the MDMS model to study subcutaneous injection of mAbs. We investigate model parameters that contribute significantly to volume of drug entering the septa network which are paths to lymphatics. Our results show that septa play a critical role in the transport of mAbs in the subcutaneous tissue.

This paper is organized as follows. Section 2 introduces the MDMS poroelastic model. Numerical methods are discussed in Sect. 3. The MDMS poroelastic model is verified in Sect. 4, and is applied to study subcutaneous injection in Sect. 5. Finally, Sect. 6 summarizes the findings of this work.

2 Model equations

In this section, we present the MDMS poroelastic model for the adipose tissue. The tissue matrix is modeled using the full-dimensional poroelastic model with drug transport in the tissue matrix. The septa are modeled using a reduced-dimension model.

We introduce first some notations that are used throughout the rest of the paper. Let $\Omega \subset \mathbb {R}^{{d }}$, where ${d }= 2, 3$ is the spatial dimension, be an open and bounded domain with Lipschitz boundary $\partial \Omega$. Let $\Gamma \subset \mathbb {R}^{\text {d}-1}$ be a co-dimension one subspace of $\Omega$. The domain of the tissue matrix is represented by $\Omega$, while $\Gamma$ is the septa interface embedded in the matrix. Denote time as $t \in (0, T]$, where $T > 0$ is the time when the injection ends.

2.1 Full-dimensional model for the tissue

The poroelastic model (Biot 1941, 1956; Biot and Temple 1972) with fluid transport (Kadeethum et al. 2021; Rudraraju et al. 2013; Tran and Jha 2020), is used to model the adipose tissue. We assume that the mechanical response of the tissue matrix and fluid flow therein can be characterized using the homogeneous macroscale poroelastic model. Under quasi-static conditions and negligible gravitational effects (Biot 1941, 1956; Biot and Temple 1972; Coussy 2004; Fornells et al. 2007; Kadeethum et al. 2021; Tran and Jha 2020), the equation of linear momentum in the tissue matrix can be written as

$$\begin{aligned}&\nabla \cdot {\varvec{\sigma }}({\varvec{u}}, p) = {\varvec{0}}, \text { with } {\varvec{\sigma }}({\varvec{u}}, p) = {\varvec{\sigma }}^{\text {eff}}({\varvec{u}}) - \alpha p {\textbf {I}},\nonumber \\&\quad \text { in } \Omega \times (0, T], \end{aligned}$$

(1)

where ${\varvec{\sigma }}$ and ${\varvec{\sigma }}^{\text {eff}}$ are the total Cauchy stress and effective stress tensors, respectively, ${\varvec{u}}$ is the solid displacement, p is the pore pressure, $\alpha$ is the Biot coefficient, and I is the ${d }\times {d }$ identity tensor. We assume the tissue deformation is small, thus the effective stress ${\varvec{\sigma }}^{\text {eff}}$ can be linearized as,

$$\begin{aligned} {\varvec{\sigma }}^{\text {eff}} ({\varvec{u}}) = 2G{\varvec{\epsilon }} ({\varvec{u}}) + \lambda (\nabla \cdot {\varvec{u}}) {\textbf {I}}, \text { with } {\varvec{\epsilon }}({\varvec{u}}) = \frac{1}{2}\left( \nabla {\varvec{u}} + \nabla {\varvec{u}}^T \right) , \end{aligned}$$

where G and $\lambda$ are the Lamé coefficients, and ${\varvec{\epsilon }}$ is the symmetric linear elastic strain. The Biot coefficient is defined as

$$\begin{aligned} \alpha = 1 - \frac{K}{K_s}, \end{aligned}$$

(2)

where K is the drained modulus of the tissue, and $K_s$ is the bulk modulus of the solid constituent.

Then, the conservation of mass is given as

$$\begin{aligned} \frac{1}{M} \frac{\partial p}{\partial t} + \alpha \frac{\partial \epsilon _v}{\partial t} + \nabla \cdot {\varvec{w}} = {q}_f , \text { in } \Omega \times (0, T], \end{aligned}$$

(3)

where M is the Biot modulus, $\epsilon _v := \text {tr}({\varvec{\epsilon }}) = \nabla \cdot {\varvec{u}}$ is the volumetric strain, $q_f$ is the source term modeling fluid injection, and ${\varvec{w}}$ is the Darcy velocity

$$\begin{aligned} {\varvec{w}} = - \mathcal {K}_m \nabla p, \text { with } \mathcal {K}_m = \frac{k_m}{\mu _f}. \end{aligned}$$

(4)

Herein, $\mathcal {K}_m$ is the hydraulic conductivity of the matrix, $k_m$ is the permeability of the matrix, $\mu _f$ is the viscosity of the fluid. The Biot modulus is given by

$$\begin{aligned} \frac{1}{M} = \phi _0 c_f + \frac{\alpha - \phi _0}{K_s}, \end{aligned}$$

(5)

where $\phi _0$ is the porosity in the undeformed tissue, and $c_f$ is the fluid compressibility.

We proceed next with the governing equation for drug transport. Let c and $\widetilde{c}_0$ (mg/mL) be the concentration of mAbs in the tissue and the initial concentration of mAbs in the syringe, respectively. We use a dimensionless quantity $C = c/\widetilde{c}_0$ to represent the drug concentration in the tissue. Before injection, $C = 0$ everywhere in the tissue. During injection, $C=1$ at the injection site. The advection--diffusion equation for drug transport is given by

$$\begin{aligned} \frac{\partial }{\partial t}(\phi C) + \nabla \cdot \left( {\varvec{w}} C \right) + \nabla \cdot \left( \phi D \nabla C \right) = q_f, \text { in } \Omega \times (0, T], \end{aligned}$$

(6)

where $\phi$ is the current porosity, and D is the diffusion coefficient of mAbs inside the skin tissue. The current porosity $\phi$ is the key to couple solid deformation with drug transport. We follow (Kadeethum et al. 2021; Tran and Jha 2020) to calculate $\phi$ as

$$\begin{aligned} \phi = \phi _0 + \frac{1}{M}(p - p_0) + (\alpha -\phi _0) (\epsilon _v - \epsilon _{v,0}). \end{aligned}$$

(7)

Therein, $p_0$ and $\epsilon _{v,0}$ are the initial pressure and volumetric strain, respectively.

Finally, we assume both fluid and solid constituents in the tissue matrix are incompressible, namely $c_f =0$ and $K_s = \infty$. As a result, $1/M = 0$ and $\alpha = 1$. The diffusion coefficient of mAbs is in the order of $10^{-7}\,\hbox {cm}^2$/s (Hung et al. 2019; Wright et al. 2018), while the injection velocity at the injection site is larger than 1.0 m/s (de Lucio et al. 2020). During the injection process, convection is the dominant drug transport mechanism compared to diffusion. Therefore, we neglect the diffusion of mAbs by letting $D =0$. In summary, we arrive at the following governing equations for the tissue matrix,

$$\begin{aligned} \nabla \cdot \left( {\varvec{\sigma }}^{\text {eff}} -p {\textbf {I}} \right)&= {\varvec{0}}, \quad \text { in } \Omega \times (0, T], \end{aligned}$$

(8a)

$$\begin{aligned} \displaystyle \frac{\partial \epsilon _v}{\partial t} + \nabla \cdot {\varvec{w}}&= {q}_f , \quad \text { in } \Omega \times (0, T], \end{aligned}$$

(8b)

$$\begin{aligned} \frac{\partial }{\partial t}(\phi C) + \nabla \cdot \left( {\varvec{w}} C \right)&= q_f, \quad \text { in } \Omega \times (0, T]. \end{aligned}$$

(8c)

2.2 A reduced-dimension model for septa

As shown in Fig. 1b, septa fibers form preferential channels for fluid flow. For this reason, we model the fluid flow along the fibrous septa explicitly. We introduce more notations before presenting the model. As shown in Fig. 2a, ${\varvec{n}}_\Gamma$ is the outward unit normal of $\Gamma$, and ${\varvec{t}}_\Gamma$ is the unit vector in the tangential direction of $\Gamma$. For a scalar function $\varphi$, the jump across $\Gamma$ is defined as

$$\begin{aligned} \llbracket \varphi \rrbracket = \varphi _+ - \varphi _-, \end{aligned}$$

(9)

where

$$\begin{aligned}&\varphi _+({\varvec{x}}) = \lim _{\epsilon \rightarrow 0^+} \varphi ({\varvec{x}} + \epsilon {\varvec{n}}_\Gamma ), \text { and } \varphi _-({\varvec{x}}) \nonumber \\&\quad = \lim _{\epsilon \rightarrow 0^+} \varphi ({\varvec{x}} - \epsilon {\varvec{n}}_\Gamma ), \quad {\varvec{x}} \in \Gamma . \end{aligned}$$

(10)

For a vector-valued function ${\varvec{v}}$, the jump in the direction normal to $\Gamma$ is defined by

$$\begin{aligned} \llbracket {\varvec{v}} \cdot {\varvec{n}} \rrbracket = {\varvec{v}}_+ \cdot {\varvec{n}}_+ + {\varvec{v}}_- \cdot {\varvec{n}}_-, \end{aligned}$$

(11)

where ${\varvec{n}}_+ = -{\varvec{n}}_\Gamma$ and ${\varvec{n}}_- = {\varvec{n}}_\Gamma$.

Fig. 2

a A bundle of septa $\Gamma \subset \mathbb {R}^{{d }-1}$ embedded in the tissue matrix $\Omega \subset \mathbb {R}^{{d }}$. b Partition of elements and element faces based on their intersection with septa

We further assume that the fluid in the septa is incompressible, and that the deformation of the septa can be described by the deformation of the homogeneous tissue matrix. A reduced-dimension model, for fluid flow and transport along fractures that are embedded in rigid porous media, was proposed in Fumagalli and Scotti (2013) and Martin et al. (2005). We extend the model therein to describe fluid flow and drug transport in deformable porous tissue. The equation of conservation of mass along the septa is given as

$$\begin{aligned} \left\{ \begin{array}{l} w_d \frac{\partial \epsilon _{v,\Gamma } }{\partial t} + \nabla _\Gamma \cdot {\varvec{w}}_\Gamma = {q}_\Gamma + \llbracket {\varvec{w}} \cdot {\varvec{n}} \rrbracket , \\ \llbracket p \rrbracket = \hat{p}, \end{array} \right. \text { on } \Gamma \times (0, T], \end{aligned}$$

(12)

where $w_d$ is the width of $\Gamma$, $\epsilon _{v,\Gamma } := \epsilon _{v}|_{\Gamma }$, $\nabla _{\Gamma } := {\varvec{P}} \nabla$ is the tangential gradient and ${\varvec{P}} = \left( {\textbf {I}} - {\varvec{n}}_\Gamma \otimes {\varvec{n}}_\Gamma \right)$ is the tangential projection, $q_\Gamma$ is the fluid injection inside the septa, $\hat{p}$ is the pressure jump across $\Gamma$, and ${\varvec{w}}_{\Gamma }$ is the Darcy velocity along the septa. Herein, the Darcy velocity along the septa is defined similar to Eq. (4),

$$\begin{aligned} {\varvec{w}}_\Gamma = -\mathcal {K}_{\Gamma }\nabla _\Gamma p, \text { with } \mathcal {K}_{\Gamma } = \frac{k_{\Gamma }}{\mu _f}w_d, \end{aligned}$$

(13)

where $\mathcal {K}_\Gamma$ and $k_\Gamma$ are the hydraulic conductivity and permeability in the tangential direction of the septa, respectively. The last term in Eq. (12) models the fluid exchange between the tissue matrix and the septa.

Let $C_\Gamma$ denote the dimensionless drug concentration inside the septa. The equation of drug transport along the septa (Fumagalli and Scotti 2013; Odsæter et al. 2019) is given by

$$\begin{aligned}&w_d \frac{\partial }{\partial t}(\phi _\Gamma C_\Gamma ) + \nabla _\Gamma \cdot \left( {\varvec{w}}_\Gamma C_\Gamma \right) - \llbracket {\varvec{w}} \cdot {\varvec{n}} C^*\rrbracket = q_\Gamma ,\nonumber \\&\quad \text { on } \Gamma \times (0, T], \end{aligned}$$

(14)

where $\phi _\Gamma := \phi |_{\Gamma }$ is the current porosity in the septa, $\llbracket {\varvec{w}} \cdot {\varvec{n}} C^*\rrbracket$ is the drug concentration change between the tissue matrix and the septa, and $C^*$ is the upwind concentration, defined as

$$\begin{aligned} C^* = {\left\{ \begin{array}{ll} C_\pm , &{}\text {if } {\varvec{w}}_\pm \cdot {\varvec{n}}_\pm \ge 0, \\ C_\Gamma , &{}\text {otherwise} , \end{array}\right. } \text { on } \Gamma \times (0, T]. \end{aligned}$$

(15)

We assume that the septa have a higher hydraulic conductivity than the matrix, and that the pressure is continuous across the septa, i.e., $\hat{p}=0$. As a result, continuous finite elements can be used for spatial discretization. Note that the assumption of continuous pressure can be relaxed to include discontinuous pressure across the septa (Capatina et al. 2016; Fumagalli and Scotti 2013). We additionally assume that the injection site is located in the tissue matrix, thus we obtain $q_\Gamma = 0$. The new model, for fluid flow and drug transport along the septa embedded in deformable porous tissue, is summarized as

$$\begin{aligned}&\displaystyle w_d \frac{\partial \epsilon _{v,\Gamma }}{\partial t} + \nabla _\Gamma \cdot {\varvec{w}}_\Gamma = \llbracket {\varvec{w}} \cdot {\varvec{n}} \rrbracket , \quad \text { on } \Gamma \times (0, T], \end{aligned}$$

(16a)

$$\begin{aligned}&\llbracket p \rrbracket = 0, \quad \text { on } \Gamma \times (0, T], \end{aligned}$$

(16b)

$$\begin{aligned}&w_d \frac{\partial }{\partial t} \left( \phi _\Gamma C_\Gamma \right) + \nabla _\Gamma \cdot \left( {\varvec{w}}_\Gamma C_\Gamma \right) = \llbracket {\varvec{w}} \cdot {\varvec{n}} C^*\rrbracket , \quad \text { on } \Gamma \times (0, T]. \end{aligned}$$

(16c)

Equations (8) and (16) together are the proposed MDMS poroelastic model for the adipose tissue. Equation () describes the poroelastic behavior and fluid transport of the macroscale tissue matrix, while Eq. (16) models the fluid flow and drug transport along the microscale septa.

3 Numerical methods

In this section, we briefly introduce the numerical methods, including temporal and spatial discretizations, and solution algorithms, used in this work. The numerical methods are implemented using the open-source finite element library deal.II (Arndt et al. 2020; Bangerth et al. 2007; Bause et al. 2017; Odsæter et al. 2019).

3.1 Temporal discretization

The implicit second-order backward differentiation formula, denoted as $\text {BDF}_2$, is adopted for temporal discretization. For a scalar function $\varphi$, we have

$$\begin{aligned} \frac{\partial \varphi }{\partial t} \approx \text {BDF}_2(\varphi ^n) = \frac{1}{2 \Delta t} \left( 3 \varphi ^n - 4 \varphi ^{n-1} + \varphi ^{n-2}\right) , \end{aligned}$$

(17)

where $\Delta t = t^n - t^{n-1}$ is the uniform time step between time $t^n$ and $t^{n-1}$, for $n \ge 1$, and $\varphi ^n \approx \varphi (t^n)$.

3.2 Spatial discretization

We introduce next the spatial discretization. For the rest of the work, we limit ourselves to two dimensions, ${d }=2$. Let $\mathcal {T}_h$, consisting of quadrilateral polygons, be a conforming, shape-regular, and quasi-uniform triangulation of $\Omega$. We decompose the boundary $\partial \Omega$ into Dirichlet and Neumann boundaries as

$$\begin{aligned}&\partial \Omega = \partial \Omega ^{{\varvec{u}}}_{\text {D}} \cup \partial \Omega ^{{\varvec{u}}}_{\text {N}} = \partial \Omega ^{p}_{\text {D}} \cup \partial \Omega ^{p}_{\text {N}}, \text { and } \partial \Omega ^{{\varvec{u}}}_{\text {D}} \cap \partial \Omega ^{{\varvec{u}}}_{\text {N}}\nonumber \\&\quad = \partial \Omega ^{p}_{\text {D}} \cap \partial \Omega ^{p}_{\text {N}} = \emptyset , \end{aligned}$$

(18)

where $\partial \Omega ^{{\varvec{u}}}_{\text {D}}$ and $\partial \Omega ^{{\varvec{u}}}_{\text {N}}$ are the Dirichlet and Neumann boundaries for solid displacement, while $\partial \Omega ^{p}_{\text {D}}$ and $\partial \Omega ^{p}_{\text {N}}$ are the Dirichlet and Neumann boundaries for pressure. We remark that drug can only enter or exit the tissue with the fluid. Thus, the boundary conditions for drug concentration follow the fluid velocity.

Following (Odsæter et al. 2019), we distinguish between $\mathcal {T}_h^{\text {S}} = \left\{ K \in \mathcal {T}_h : K \cap \Gamma \ne \emptyset \right\}$ and $\mathcal {T}_h^{\text {M}} = \mathcal {T}_h \backslash \mathcal {T}_h^{\text {S}}$ as illustrated in Fig. 2b. Define $\mathcal {F}_h$ as the set of all element faces. Then, $\mathcal {F}_h$ can be divided into $\mathcal {F}_h = \mathcal {F}_{h, \text {D}} \cup \mathcal {F}_{h, \text {N}} \cup \mathcal {F}_{h, \text {I}}$ where $\mathcal {F}_{h, \text {D}} \cap \mathcal {F}_{h, \text {N}} \cap \mathcal {F}_{h, \text {I}} = \emptyset$. Herein, $\mathcal {F}_{h, \text {D}}$ and $\mathcal {F}_{h, \text {N}}$ are the element faces on the Dirichlet ($\partial \Omega ^{p}_{\text {D}}$) and Neumann $\partial \Omega ^{p}_{\text {N}}$ boundaries for pressure, respectively; $\mathcal {F}_{h, \text {I}}$ is the set of element faces that are in the interior of the domain. Moreover, we have $\mathcal {F}_{h, \text {I}} = \mathcal {F}_{h, \text {I}}^{\text {S}} \cup \mathcal {F}_{h, \text {I}}^{ \text {M}}$ as shown in Fig. 2b. In addition, we define the inner product on $\mathcal {T}_h$ and $\mathcal {F}_h$ respectively as

$$\begin{aligned} \left( \cdot , \cdot \right) _{\mathcal {T}_h} = \sum _{K \in \mathcal {T}_h} (\cdot , \cdot )_K, \quad \left( \cdot , \cdot \right) _{\mathcal {F}_h} = \sum _{F \in \mathcal {F}_h} (\cdot , \cdot )_F, \end{aligned}$$

(19)

where $(\cdot , \cdot )_O$ is the inner product over the object O which can be an element $K \in \mathcal {T}_h$, or an element face $F \in \mathcal {F}_h$.

3.2.1 Poroelastic equations

We adopt the Galerkin method for spatial discretization of the poroelastic model. More specifically, continuous Galerkin (CG) is used for the conservation of linear momentum and conservation of mass equations. The finite element spaces are defined as

$$\begin{aligned} {\varvec{V}}_h&:= \left\{ {\varvec{v}}_h \in \left[ H^1(\Omega )\right] ^{{d }} : {\varvec{v}}_h|_{K} \in \left[ \mathbb {P}_1 (K)\right] ^{{d }},\right. \nonumber \\&\quad \left. \forall K \in \mathcal {T}_h, {\varvec{v}}_h|_{\partial \Omega ^{{\varvec{u}}}_{\text {D}}} = {\varvec{0}} \right\} , \end{aligned}$$

(20a)

$$\begin{aligned} Q_{1,h}&:= \left\{ \theta _h \in H^1(\Omega ) : \theta _h|_{K} \in \mathbb {P}_1 (K),\right. \nonumber \\&\quad \left. \forall K \in \mathcal {T}_h, \theta _h|_{\partial \Omega ^{p}_{\text {D}}} = 0 \right\} , \end{aligned}$$

(20b)

where $H^1$ is the classical Sobolev space, and $\mathbb {P}_r$ denotes polynomials of order $r \ge 0$.

The weak form of the conservation of linear momentum Eq. (8a) is given as

$$\begin{aligned} \left( {\varvec{\sigma }}({\varvec{u}}_{h}^n, p_h^n), \nabla {\varvec{v}}_h \right) _{\mathcal {T}_h} = \left( {\varvec{\sigma }}({\varvec{u}}_{h}^n, p_h^n) \cdot {\varvec{n}}, {\varvec{v}}_h \right) _{\partial \Omega ^{{\varvec{u}}}_{\text {N}}}, \quad \forall {\varvec{v}}_h \in {\varvec{V}}_h. \end{aligned}$$

(21)

Similarly, the weak form of the conservation of mass Eqs. (8b) and (16a) can be written as (Burman et al. 2019; Odsæter et al. 2019)

$$\begin{aligned} \begin{aligned}&\left( \text {BDF}_2(\epsilon ^n_v), \theta _h \right) _{\mathcal {T}_h} - \left( {\varvec{w}}^{n} (p^n_h), \nabla \theta _h \right) _{\mathcal {T}_h} \\&\quad + \left( \text {BDF}_2(\epsilon ^n_{v,\Gamma }) w_d, \theta _h \right) _{\Gamma \cap \mathcal {T}_h} - \left( {\varvec{w}}_\Gamma ^{n}(p^n_h), \nabla _\Gamma \theta _h \right) _{\Gamma \cap \mathcal {T}_h} \\&= \left( q_f, \theta _h \right) _{\mathcal {T}_h} - \left( w_{\text {N}}, \theta _h\right) _{\partial \Omega ^p_{\text {N}}} \\&\quad - \sum _{{\varvec{x}} \in \Gamma \cap \partial \Omega ^p_{\text {N}}} w_d w_{\text {N}}({\varvec{x}}) \theta _h({\varvec{x}}), \quad \forall \theta _h \in Q_{1,h}. \end{aligned} \end{aligned}$$

(22)

where $w_{\text {N}}$ is the boundary data for Darcy velocity, and we have used the following notations $\epsilon ^n_v = \epsilon _v({\varvec{u}}^n_h)$, $\epsilon ^n_{v,\Gamma } = \epsilon _{v,\Gamma }({\varvec{u}}^n_h)$.

3.2.2 Darcy velocity approximation

Before presenting the weak form of the transport Eqs. (8c) and (16c), we need to calculate the discrete Darcy velocity ${\varvec{w}}$ and ${\varvec{w}}_\Gamma$. Because the discrete pressure field is only piece-wise continuous, we instead take the average of the velocity across an element face as follows:

$$\begin{aligned} W^n_h = \left\{ \begin{array}{ll} - \mathcal {K}_e \left\{ \!\!\left\{ \nabla p^n_h \cdot {\varvec{n}}_F \right\} \!\!\right\} , &{}\quad {\text {on}}\, F \in \mathcal {F}_h \backslash \left( \mathcal {F}^{\text {S}}_{h,\text {I}} \cup \mathcal {F}_{h,\text {N}} \right) , \\ -\frac{1}{|F|} \left\{ \!\!\left\{ \kappa _\Gamma \nabla _\Gamma p^n_h \cdot {\varvec{t}}_\Gamma \right\} \!\!\right\} , &{}\quad {\text {on}}\; F \in \mathcal {F}^{\text {S}}_{h,\text {I}},\\ w_{\text {N}}, &{}\quad {\text {on}}\; F \in \mathcal {F}_{h,\text {N}}, \end{array} \right. \end{aligned}$$

(23)

where $\mathcal {K}_e = \frac{2 \mathcal {K}_+ \mathcal {K}_-}{\mathcal {K}_+ + \mathcal {K}_-}$ is the harmonic average of the hydraulic conductivity $\mathcal {K}$ of the element K at the element face $F \subset K$. More specifically, $\mathcal {K} = \mathcal {K}_m$ if $K \in \mathcal {T}^{\text {M}}_h$, and $\mathcal {K} = \mathcal {K}_\Gamma$ if $K \in \mathcal {T}^{\text {S}}_h$. Additionally, in Eq. (23), ${\varvec{n}}_F$ is the unit vector outward normal of F, $|(\cdot )|$ denotes the measure of $(\cdot )$, and for a scalar function $\varphi$, $\{\!\!\{ \cdot \}\!\!\}$ is the arithmetic average operator

$$\begin{aligned} \left\{ \!\!\left\{ \varphi \right\} \!\!\right\} = \frac{1}{2} \left( \varphi _+ + \varphi _-\right) . \end{aligned}$$

(24)

We remark that in Eq. (23) for $F \in \mathcal {F}^{\text {S}}_{h,\text {I}}$, we have used the following approximation $W^n_h |_F \approx W^n_h|_{F \cap \Gamma }$ because $W^n_h |_{F\backslash \Gamma } \ll W^n_h|_{F \cap \Gamma }$.

It is well-known that Eq. (23) obtained using piece-wise continuous approximation of the pressure field is not locally mass-conservative, and that applying Eq. (23) in conjunction with the DG method to the transport equation leads to artificial source and sink terms (Kadeethum et al. 2021; Sun and Wheeler 2006). A common resolution is to postprocess $W^n_h$ as follows:

$$\begin{aligned} V^n_h = \left\{ \begin{array}{ll} W^n_h + \mathcal {K}_e \llbracket y^n\rrbracket , &{} \quad {\text {on}}\; F \in \mathcal {F}_h \backslash \mathcal {F}_{h,\text {N}}, \\ w_{\text {N}}, &{}\quad {\text {on}}\; F \in \mathcal {F}_{h,\text {N}}, \end{array} \right. \end{aligned}$$

(25)

which is continuous across element faces, and satisfies the local mass conservation condition on each element. In Eq. (25), $y^n \in Q_{0,h}$ is the unique solution of the following equation (Odsæter et al. 2017)

$$\begin{aligned} \left( \mathcal {K}_e \llbracket y^n\rrbracket , \llbracket z \rrbracket \right) _{\mathcal {F}_h \backslash \mathcal {F}_{h,\text {N}}} = \left( \mathcal {R}(W^n_h), z\right) _{\mathcal {T}_h}, \forall z \in Q_{0,h}, \end{aligned}$$

(26)

where

$$\begin{aligned} Q_{0,h} := \left\{ \psi _h \in L^2(\Omega ) : \psi _h|_{K} \in \mathbb {P}_0 (K), \forall K \in \mathcal {T}_h, \right\} , \end{aligned}$$

(27)

is the classical Lebesgue space,

$$\begin{aligned} \mathcal {R}(W^n_h)|_K = \left\{ \begin{array}{ll} \frac{1}{|K|} \left( \int _K \left( q_f - \text {BDF}_2(\epsilon ^n_v) \right) {\mathrm{d}} V - \int _{\partial K }W^n_h {\varvec{n}}_F \cdot {\varvec{n}}_K {\mathrm{d}} S \right) , &{}\quad K \in \mathcal {T}^{\text {M}}_h , \\ \frac{1}{|K|} \left( \int _{K \cap \Gamma } \left( -\text {BDF}_2(\epsilon ^n_{v,\Gamma })w_d \right) {\mathrm{d}} S - \int _{\partial K }W^n_h {\varvec{n}}_F \cdot {\varvec{n}}_K {\mathrm{d}} S \right) , &{}\quad K \in \mathcal {T}^{\text {S}}_h, \end{array} \right. \end{aligned}$$

(28)

is the residual of the equation of conservation of mass, and measures the flux discrepancy from local mass conservation. In Eq. (28), ${\varvec{n}}_K$ in the unit vector outward normal of the element K.

3.2.3 Transport equations

Finally, we are ready to present the weak form of the transport equations. Because the transport equations (8c) and (16c) are convection-dominated problems (Kadeethum et al. 2021; Rudraraju et al. 2013; Tran and Jha 2020), continuous Galerkin methods and central finite difference methods result into oscillations of the concentration field. It is necessary to use advanced numerical methods as in Brooks and Hughes (1982), Hughes et al. (1989) and Leng et al. (2022). We use the discontinuous Galerkin (DG) method with upwind scheme to ensure numerical stability. Thus, we did not observe any numerical instabilities of the concentration field. As discussed in Odsæter et al. (2019), the zeroth-order DG method is equivalent to the finite volume method. Thus, we present the finite volume formulation for the transport equations for simplicity,

$$\begin{aligned} \begin{aligned}&\sum _{K \in \mathcal {T}^{\text {M}}_h} \int _K \text {BDF}_2(\phi ^n C_h^n) {\mathrm{d}} V + \sum _{K \in \mathcal {T}^{\text {S}}_h} \int _{K\cap \Gamma } \text {BDF}_2(\phi _\Gamma ^n C_h^n)w_d \, {\mathrm{d}} S \\&\quad + \sum _{K \in \mathcal {T}_h} \int _{\partial K} V^n_h C_h^{n} {\varvec{n}}_K \cdot {\varvec{n}}_F \, {\mathrm{d}} S = \sum _{K \in \mathcal {T}_h} \int _K q_f \, {\mathrm{d}} V. \end{aligned} \end{aligned}$$

(29)

To derive Eq. (29), we have used the approximation

$$\begin{aligned} \int _{K \cap \Gamma } \llbracket {\varvec{w}} \cdot {\varvec{n}} C_h^* \rrbracket {\mathrm{d}} S \approx \sum _{\hat{K} \in \mathcal {T}^{\text {M}}_h} \int _{\partial \hat{K} \cap \partial K} {\varvec{w}} \cdot {\varvec{n}} C_h {\mathrm{d}} S, \end{aligned}$$

(30)

and more details can be found in Odsæter et al. (2019). It is worth noting that for $K \in \mathcal {T}^{\text {M}}_h$, we have let $C_h$ be the drug concentration in the tissue matrix; for $K \in \mathcal {T}^{\text {S}}_h$, we have let $C_h$ represent the drug concentration in the septa.

3.3 Solution algorithm

The fixed-stress splitting algorithm solves the poroelastic equations sequentially (Kim et al. 2009, 2011), thus it allows the use of different numerical methods and preconditioners for the conservation of linear momentum Eq. (8a) and conservation of mass Eq. (8b). Because the poroelastic and transport models are weakly coupled, we apply the fixed-stress splitting algorithm to solve the linear poroelastic model Eqs. (21) and (22). After obtaining the solid displacement and pore pressure, we proceed to solve the transport equation (29). A similar solution algorithm can be found in Kadeethum et al. (2021) and Tran and Jha (2020). The solution algorithm is summarized in Algorithm 1.

4 Model verification

In this section, we verify the MDMS poroelastic model, Eqs. (8) and (16), by comparing simulation results against the full 2D model, Eq. (8) for ${d }=2$, where the septa are resolved using fine meshes. We focus on the vertical plane that is perpendicular to the skin surface, and assume plane strain condition.

Taking $\Omega = (0, 0.01 \text { m})^2$, see Fig. 3a, we assume there are six septa inside the tissue. If not stated otherwise, the units for length and position are meter (m) and are omitted for the rest of the work. Following (Leng et al. 2021b), we choose the following model parameters of the tissue matrix $E = 10$ kPa, $\nu = 0.49$, $\phi _0= 0.2$, $\mu _f = 1$ cP, and $k_m = 1 \times 10^{-14}$ m$^2$. In this verification example, the drug is injected uniformly from the left boundary, $x=0$, thus we have $q_f = 0$. The fluid is free to flow out of the tissue sample from the right boundary, $x = 0.01$. The top surface of the tissue is subjected to compression. The boundary conditions are

$$\begin{aligned} \left\{ \begin{array}{ll} \nabla p \cdot {\varvec{n}} = - w_{\text {N}}, \text { } \quad {\varvec{u}} \cdot {\varvec{n}} = 0, \left( {\varvec{\sigma }}^{\text {eff}} {\varvec{n}}\right) \cdot {\varvec{t}} =0, &{}\quad {\text {on}}\; x = 0, \\ p = 0, \quad {\varvec{\sigma }}^{\text {eff}} {\varvec{n}} = {\varvec{0}}, &{}\quad {\text {on}}\; x = 0.01,\\ \nabla p \cdot {\varvec{n}} = 0, \quad {\varvec{\sigma }}^{\text {eff}} {\varvec{n}} = {\varvec{0}}, &{}\quad {\text {on}}\; y = 0, \\ \nabla p \cdot {\varvec{n}} = 0, \quad {\varvec{\sigma }}^{\text {eff}} {\varvec{n}} = {\varvec{T}}, &{}\quad {\text {on}}\; y = 0.01, \end{array} \right. \end{aligned}$$

(31)

where $w_{\text {N}} = 0.01$ m/s, and ${\varvec{T}} = [0, -1.0 \text { Pa}]^T$. We impose the drug concentration $C=1$ at the inflow boundary $x=0$. Taking uniform time step $\Delta t = 0.00001$ s, we study the drug distribution in the tissue and along the septa at $t = 0.5$ s.

To verify the model, we assume that all the septa have the same constant width $w_d=15.625\,\upmu$m Comley and Fleck (2010). We assume additionally that the permeability along the septa is $k_{\Gamma } = 1 \times 10^{-9}\,\hbox {m}^2$. We consider septa fibers that are aligned with one of the Cartesian coordinates. It is worth nothing that the orientation of the septa in the MDMS model can be arbitrary. This assumption for septa orientation is for verification only. As a result, the septa can be resolved using fine meshes for the full 2D model. An adaptively refined coarse mesh is shown in Fig. 3b, which is the base for all mesh refinements. Three local mesh refinements near the septa are further shown in Fig. 3c–e. In Fig. 3c, the smallest mesh size, h, is twice as large as the septa width $w_d$. Figure 3d, e demonstrate mesh refinements for $h=w_d$ and $h=0.5w_d$, respectively. As shown in Fig. 3c–e, we have used adaptively refined meshes in order to achieve more accurate solutions near the septa. Other similar techniques such as T-splines and B-Splines-based isogeometric analysis (Casquero et al. 2017, 2018) can also be applied to our proposed MDMS model.

We first solve the full 2D model, Eq. (8), using finest mesh refinements as shown in Fig. 3e. The solution of the full 2D model is regarded as reference solution because the septa are resolved explicitly using fine meshes. Then, we solve the proposed MDMS poroelastic model, Eqs. (8) and (16), using two mesh refinements presented in Fig. 3c, d, and compare numerical solutions against that of the full 2D model. The major interest of this work is to study the drug distribution in the tissue matrix and along the septa. For that reason, we present only the spatial distribution of drug concentration in the tissue at $t = 0.5$ s in Fig. 4, and discuss the pressure and vertical displacement in “Appendix”. Figure 4 shows that the numerical solutions of the MDMS model agree with the reference solution both in the matrix and along the septa. To have a quantitative comparison of the drug transport along the septa, we further show the concentration along the six septa at $t = 0.5$ s in Fig. 5. We observe that drug concentration along each septa is in good agreement with the reference solution. In conclusion, the MDMS poroelastic model presented in Sect. 2.2 can capture the fluid flow and drug transport along the septa. Thus, this model is well-suited to study the fluid flow and poroelastic response of the tissue with embedded septa.

Fig. 3

The domain in (a) contains six septa. The mesh in (b) is adaptively refined along each septa as well as near the left boundary, $x=0$. The mesh in the blue square is further shown in (c–e) for three different mesh refinements. The coordinates of the annotated points are $P_0$ (0.005, 0.005), $P_1$ (0.00625, 0.00625), and $P_2$ (0.0075, 0.0075). The septa width $w_d$ is fixed. The smallest mesh element of each refinement is denoted as h. $P_0$ is shown in each figure as a reference to (b). Note that the mesh size near the left boundary $x=0$ is the same as that along the septa

Fig. 4

Spatial distribution of concentration $C_h$ in the tissue and along the septa at $t = 0.5$ s for the MDMS and full 2D models with three mesh refinements shown in Fig. 3

Fig. 5

Concentration along the six septa shown in Fig. 3a at $t = 0.5$ s for the MDMS and full 2D models with three mesh refinements presented in Fig. 3. For the full 2D model with mesh refinement as in Fig. 3e, $h=0.5w_d$, the concentration is taken as the average across the width of the septa

5 Application to subcutaneous injection

In this section, we apply the MDMS poroelastic model to study subcutaneous injection. Using symmetry, we can simplify the problem and perform simulation on the domain that is located on half of the vertical plane. We consider a skin tissue of size $\Omega = (0,0.05 \text { m})^2$. Unless otherwise stated, the model parameters of the tissue matrix are the same as those in Sect. 4. The injection is modeled as a constant source term located at the element that includes the injection point A as shown in Fig. 2a. More details on injection modeling can be found in Leng et al. (2021a, 2021b). We choose an injection rate of $q_f = 0.4$ mL/s/m, and the duration of the injection is $T=5$ s. The skin is divided into three layers, namely, dermis, subcutis, and muscle. We assume a rectangular septa network in the adipose layer as shown in Fig. 6a. According to Comley and Fleck (2010), the septa width, $w_d$, in porcine tissue ranges from 30 $\mu$m to 10 nm, and the inter-septa distance can be of several millimeters. Even though the maximum thickness can be of several hundred microns in width for healthy non-cellulite human adipose tissue (Hexsel et al. 2009; Macchi et al. 2010; Wang et al. 2011), we are interested in the contribution of these microscale septa to drug transport. Thus, we assume that all septa in Fig. 6a have the same constant width $w_d=10\,\upmu$m, and the inter-septa distance is 1 mm.

Fig. 6

a A general septa network inside the subcuti layer of the skin. The coordinates of the three points are A (0, 0.0455), B (0.049, 0.047), and C (0.049, 0.023). The injection site is located at A. b The light pink region is adaptively refined. The dark pink region is uniformly refined (mesh not shown) and the mesh size is the same as the smallest mesh size, $h=0.00015625$ m, in the light pink region

The tissue is fixed in position at the bottom surface $y = 0$. The symmetry line is located at $x=0$. The injection takes place at 4.5 mm below the skin surface on the symmetry line, i.e., point A in Fig. 6a. Fluid can exit the tissue from the bottom and right surfaces. In summary, the boundary conditions are given as

$$\begin{aligned} \left\{ \begin{array}{ll} \nabla p \cdot {\varvec{n}} =0, \text { } \quad {\varvec{u}} \cdot {\varvec{n}} = 0, \left( {\varvec{\sigma }}^{\text {eff}} {\varvec{n}}\right) \cdot {\varvec{t}} =0, &{}\quad {\text {on}}\; x = 0, \\ p = 0, \quad {\varvec{\sigma }}^{\text {eff}} {\varvec{n}} = {\varvec{0}}, &{}\quad {\text {on}}\; x = 0.05,\\ p = 0, \quad {\varvec{u}} = {\varvec{0}}, &{}\quad {\text {on}}\; y = 0, \\ \nabla p \cdot {\varvec{n}} = 0, \quad {\varvec{\sigma }}^{\text {eff}} {\varvec{n}} = {\varvec{0}}, &{}\quad {\text {on}}\;y = 0.05. \end{array} \right. \end{aligned}$$

(32)

We take the time step to be $\Delta t = 0.001$ s. Figure 6b shows the adopted adaptive mesh refinement. Therein, we only show the region where the mesh is adaptively refined, i.e., light pink region in Fig. 6b. The dark pink region in Fig. 6b is uniformly refined but the mesh is not shown. The mesh size in the uniformly refined region, $h=0.00015625 \text { m}$, is the same as the smallest mesh size in the light pink region. As indicated in Fig. 6a, b, the mesh in the subcutis layer is fine and uniform, but the mesh size is still much larger than the septa width, $w_d= 10\,\upmu$m. There are no septa in the muscle layer which justifies the use of the coarse mesh.

The ultimate goal of studying subcutaneous injection is to predict drug uptake. Drug solutions composed of mAbs are absorbed mainly through lymphatics, and fibrous septa are prelymphatic pathways (Klein 2000; Ryan 1989). Therefore, it is critical to study drug distribution inside the septa network because drug inside the septa network indicates the amount of drug that is more likely to be absorbed by the lymphatics. For all these reasons, we define a metric

$$\begin{aligned} \frac{V_{\text {sep.}}}{V_{\text {inj.}}} \times 100 \%, \end{aligned}$$

(33)

where $V_{\text {sep.}}$ is the volume of drug residing in the septa network, and $V_{\text {inj.}}$ is the total injected drug volume. Equation (33) measures the fraction of injected drug that enters the septa network. Here, we study factors, such as permeability, septa width, inter-septa distance, and concentration-dependent drug viscosity, that change the volume fraction of drug inside the septa network.

We first study the effect of the permeability. Instead of limiting ourselves to the absolute value of $k_m$ and $k_\Gamma$, we focus on the permeability ratio between the septa and the tissue matrix,

$$\begin{aligned} k_r = \frac{k_{\Gamma }}{k_m}. \end{aligned}$$

(34)

By fixing $k_m = 1 \times 10^{-14}$ m$^2$ and changing $k_\Gamma$, we investigate how the permeability ratio $k_r$ changes the volume fraction of injected drug inside the septa network. As presented in Fig. 7a, if the permeability ratio is small, $k_r = 100$, less than $10\%$ of the drug enters the septa. The volume fraction of the drug that enters the septa increases with $k_r$. However, there is no further increase in drug volume inside the septa when $k_r$ is greater or equal to 100,000, where about $80\%$ of injected drug occupies the septa at the end of the injection.

Next, we study the effect of septa width $w_d$ on drug distribution. As shown in Fig. 7b, changing the septa width from 10 to 1 $\upmu$m dramatically alters the volume fraction of the drug entering the septa network, namely, from 80 to 20% at the end of the injection. Septa width is directly related to the volume capacity of the septa network. When $w_d = 1\,\upmu$m, the volume fraction of the drug in the septa network increases initially to 40% at $t = 2$ s, then drops to $20\%$ at $t = 5$ s. This is due to the fact that the maximum volume capacity of the septa network is reached and later the drug travels from the septa to the matrix. This illustrates a non-trivial mechanism of drug transport whereby the drug can reach distant locations in the matrix traveling quickly through the septa and then going from the septa to the matrix.

Fig. 7

Effect of the permeability ratio, $k_r$, and septa width w on drug distribution. In (a), $w_d=10\,\upmu$m, $d_{\overline{w}}=1$ mm, $\mu _f = 1$ cP. In (b), $k_r=100{,}000$, $d_{\overline{w}}=1$ mm, $\mu _f = 1$ cP. The gray shaded region indicates the duration of the injection

Fig. 8

Red lines represent septa embedded in the tissue matrix. The width of the septa is exaggerated. a Change $d_{\overline{w}}$ only, $w_d$ is kept constant. b Change $d_w$ and $w_d$, keep the ratio $d_w / w_d$ constant

Now, we study how the inter-septa distance affects drug distribution. First of all, we let the septa width be $w_d=10\,\upmu$m but change the inter-septa distance, denoted as $d_{\overline{w}}$, from 1 mm to 2 and 4 mm as shown in Fig. 8a. For a wider inter-septa distance $d_{\overline{w}}$, the total number of septa is reduced. As a result, the volume capacity of the septa network decreases. As shown in Fig. 9a, the volume fraction of drug in the septa network drops significantly. Next, as in Fig. 8b, we change both the septa width $w_d$ and inter-septa distance, denoted as $d_{w}$, so as to keep the volume capacity of the septa network approximately the same. Even though the inter-septa distance is increased and there are fewer septa in the tissue, Fig. 9b indicates that the volume fraction of drug in the septa network does not vary much if the volume capacity of the septa network is kept constant.

Fig. 9

Effect of inter-septa distance on drug distribution. In (a), $k_r =100{,}000$, $w_d=10\,\upmu$m, $\mu _f = 1$ cP. In (b), $k_r=100{,}000$, $\mu _f = 1$ cP; and for $d_{w}=1$ mm, $w_d=10\,\upmu$m; for $d_{w}=2$ mm, $w_d=20\,\upmu$m; for $d_{w}=4$ mm, $w=40\,\upmu$m. The gray shaded region indicates the duration of the injection

Fig. 10

In (a), for $\widetilde{c}_0 = 1$ mg/mL, $\mu _f = 1$ cP is constant. In (b), $k_r=100{,}000$, $w_d=10\,\upmu$m, $d_{\overline{w}}=1$ mm. The gray shaded region in (b) indicates the duration of the injection

Finally, we investigate the effect of concentration-dependent viscosity on drug distribution. We adopt the Ross-Minton equation to model the viscosity of the drug solution (Hung et al. 2019; Lilyestrom et al. 2013; Liu et al. 2005),

$$\begin{aligned} \mu _f(C) = \mu _{f0 }\exp \left( \frac{v_i \widetilde{c}_0 C}{1- v_i v_k \widetilde{c}_0 C} \right) \end{aligned}$$

(35)

where $\mu _{f0} = 1$ cP is the viscosity of the interstitial fluid, $v_i = 0.0064$ mL/mg is the intrinsic viscosity, $v_k = 0.72$ depends on the crowding factor and shape determining factor. Equation (35) is illustrated in Fig. 10a for different initial mAbs concentration, $\widetilde{c}_0 = 1, 100, 120$ and 150 mg/mL. We remark that for concentration-dependent drug viscosity, the equations of conservation mass, Eqs. (8b) and (16a), become weakly coupled with the transport Eqs. (8c) and (16c). Following (Kadeethum et al. 2021; Tran and Jha 2020), we apply explicit coupling between concentration and viscosity to solve Eq. (22) by considering

$$\begin{aligned} \mu _f = \mu _f\left( \widetilde{C}^n_h \right) , \text { where } \widetilde{C}^n_h = 2C^{n-1}_h - C^{n-2}_h . \end{aligned}$$

(36)

The mAbs concentration in the injected drug solution is gradually increased, and the drug viscosity grows exponentially. The volume fraction of drug inside the septa network is presented in Fig. 10b. When the initial mAbs concentration is increased from 1 to 120 mg/mL, the maximum drug viscosity changes from 1 to 5.6 cP and the volume fraction of drug in the septa network is reduced by $10 \%$. For high initial mAbs concentration, 150 mg/mL, the maximum drug viscosity becomes 22.4 cP and the volume fraction of the drug entering the septa network is decreased to 55%.

We have investigated numerically the effect of permeability, septa width, inter-septa distance and concentration-dependent viscosity on the drug distribution in the septa network as well as in the tissue matrix. These factors can be classified into two categories: flow resistance of the drug and volume capacity of the septa network. Permeability and concentration-dependent drug viscosity correspond to the flow resistance of the drug, while septa width and inter-septa distance are closely related to the volume capacity of the septa network. Flow resistance of the drug determines the speed the injected drug can fill the septa network. The total volume of drug that can enter the septa network depends on the volume capacity of the septa network.

6 Conclusion

In this work, we have presented a mixed-dimensional multi-scale (MDMS) poroelastic model of adipose tissue for subcutaneous injection of mAbs. The tissue matrix is modeled as a homogeneous porous media. The fibrous septa are modeled explicitly as reduced-dimension microscale interfaces embedded in the macroscale tissue matrix. The MDMS poroelastic model is verified by comparing numerical results against the full 2D model where fibrous septa are resolved by fine meshes. Spatial distribution of drug concentration in the tissue and along the septa of the MDMS and full 2D models are in good agreement. More importantly, quantitative discrepancies of the drug concentration along each the septa obtained using the two models are negligible.

Then, we have applied the MDMS poroelastic model to study subcutaneous injection of mAbs. We found that the permeability ratio between the septa and tissue matrix, volume capacity of the septa network including septa width and inter-septa distance, and concentration-dependent drug viscosity are important factors affecting the amount of drug entering the septa network. Because septa constitute prelymphatic pathways, and mAbs are primarily absorbed by lymphatic capillaries, the results have important consequences for our understanding of mAbs uptake. Our model bridges the gap between existing computational approaches to mAb transport that assume isotropic, homogenized tissue properties and experiments which clearly show a preferential transport along septa. These embedded septa give rises to a highly anisotropic and heterogeneous drug distribution in the adipose tissue.

Our results also point to a previously overlooked mechanism of drug transport that enables quick migration of the drug from the injection site to distant locations of the tissue matrix. Our data show that the drug can travel far through the septa network. Then, if the septa that are distant to the injection size are filled with drug, the drug will migrate back from the septa to the tissue matrix. Given the properties of the adipose tissue matrix and the studied injection conditions, this communication between distant locations in the tissue matrix is not possible without transport through the septa. The preferential transport of mAbs through confined spaces such as septa also highlights the importance of further studying the rheology of highly concentrated antibody solutions (Dandekar and Ardekani 2021).

In order to validate our MDMS model, subcutaneous injection experiments similar to those in Thomsen et al. (2014, 2015) should be conducted. One of the challenges for experiments is to measure drug concentration distribution in the tissue. Because mAbs have large molecular weight, small iodinated compounds, which are successfully used as contrast agents to track low molecular weight proteins (Comley and Fleck 2011; Thomsen et al. 2014, 2015), cannot be used to track mAbs. Fortunately, imaging techniques (He et al. 2020), such as positron emission tomography (Niu et al. 2009) and near-infrared fluorescence imaging (Cilliers et al. 2017), are promising in tracking mAbs distribution after subcutaneous injection.

This is the first step toward modeling fibrous septa using MDMS poroelastic models. In this work, we have assumed that the septa deformation is homogeneous as the tissue matrix. The next step is to model the solid deformation of the fibrous septa explicitly using similar ideas to those employed here for fluid flow. In addition, a simplified septa network is adopted. However, in actual adipose tissue each individual bundle of septa has its orientation, width, and length. For practical applications, it would be important to incorporate realistic septa characteristics from experiments for the study of subcutaneous injection. Finally, we have assumed the pressure is continuous thus have used continuous Galerkin for the pressure approximation. This assumption can be relaxed to consider a discontinuous pressure field. Thus, it is necessary to consider other numerical methods such as Capatina et al. (2016) and Fumagalli and Scotti (2013).

Appendix

Here, we provide additional data for the model verification presented in Sect. 4. We present spatial distributions of the vertical displacement $u_y$ in Fig. 11 and pore pressure p in Fig. 12 using the MDMS and full 2D models with three mesh refinements.

Fig. 11

Spatial distribution of vertical displacement $u_{y,h}$ in the tissue and along the septa at $t = 0.5$ s for the MDMS and full 2D models with three mesh refinements shown in Fig. 3

Fig. 12

Spatial distribution of pressure $p_h$ in the tissue and along the septa at $t = 0.5$ s for the MDMS and full 2D models with three mesh refinements shown in Fig. 3