Free vibration analysis of microtubules based on the molecular mechanics and continuum beam theory

Abstract

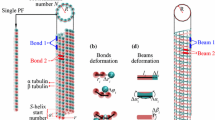
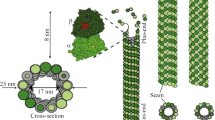
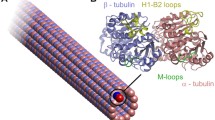
A molecular structural mechanics (MSM) method has been implemented to investigate the free vibration of microtubules (MTs). The emphasis is placed on the effects of the configuration and the imperfect boundaries of MTs. It is shown that the influence of protofilament number on the fundamental frequency is strong, while the effect of helix-start number is almost negligible. The fundamental frequency is also found to decrease as the number of the blocked filaments at boundaries decreases. Subsequently, the Euler–Bernoulli beam theory is employed to reveal the physics behind the simulation results. Fitting the Euler–Bernoulli beam into the MSM data leads to an explicit formula for the fundamental frequency of MTs with various configurations and identifies a possible correlation between the imperfect boundary conditions and the length-dependent bending stiffness of MTs reported in experiments.

Appendix

The vibration solution to Eq. 8 can be found using the method of separation of variables as

$$\begin{aligned} w(x,t)=W(x)\cdot T(t). \end{aligned}$$

(14)

Substituting Eq. 14 into Eq. 8 and rearranging yield

$$\begin{aligned} \frac{{\hbox {d}}^{2}T(t)}{{\hbox {d}}t^{2}}\frac{1}{T(t)}=-\frac{D}{\rho }\frac{{\hbox {d}}^{4}W(x)}{{\hbox {d}}x^{4}}\frac{1}{W(x)}. \end{aligned}$$

(15)

It is noted that the left term in Eq. 15 is independent with x, and the right term is independent with t. Thus, they should be equal to a constant, which is noted as $-\omega ^{2}$. Here, $\omega$ is known as the angular frequency $(f=\omega /2\pi )$.

Thus, Eq. 15 can be written as

$$\begin{aligned}&\frac{d^{2}T(t)}{{\hbox {d}}t^{2}}+\omega ^{2}T(t)=0, \end{aligned}$$

(16)

$$\begin{aligned}&\frac{d^{4}W(x)}{{\hbox {d}}x^{4}}-\tau ^{4}W(x)=0, \end{aligned}$$

(17)

where $\tau ^{4}=\rho \omega ^{2}/D$.

The solution of Eq. 17 is given by

$$\begin{aligned} W(x)= & {} C_{1}\cos (\tau x)+C_2 \sin (\tau x)\nonumber \\&+C_3 \cosh (\tau x)+C_4 \sinh (\tau x), \end{aligned}$$

(18)

where $C_{1}-C_{4}$ are constants. The constants $C_{1}-C_{4}$ and $\tau$ can be found from the boundary conditions. For the CM model of the MTs considered here, the boundary conditions can be stated as

$$\begin{aligned}&W(0)=0; \; D\frac{d^{2}W(0)}{dx^{2}}=k\frac{dW(0)}{{\hbox {d}}x}; \;\nonumber \\&\frac{d^{2}W(L)}{{\hbox {d}}x^{2}}=0; \;\frac{d^{3}W(L)}{{\hbox {d}}x^{3}}=0. \end{aligned}$$

(19)

Applying the above boundary conditions to Eq. 18 yields

$$\begin{aligned}&C_1 +C_{3}=0, \end{aligned}$$

(20)

$$\begin{aligned}&C_1 -C_3=-\frac{k}{D\tau }\left( {C_2 +C_4 } \right) , \end{aligned}$$

(21)

$$\begin{aligned}&C_1 \cos (\tau L)+C_2 \sin (\tau L)\nonumber \\&\quad +C_3 \cosh (\tau L)+C_4 \sinh (\tau L)=0, \end{aligned}$$

(22)

$$\begin{aligned}&-C_1 \sin (\tau L)+C_2 \cos (\tau L)-C_3 \sinh (\tau L)\nonumber \\&\quad +C_4 \cosh (\tau L)=0. \end{aligned}$$

(23)

Thus, we can get following characteristic equation

$$\begin{aligned}&\cos (\tau L)\cdot \cosh (\tau L)+1=\frac{D\tau }{k}[\sinh (\tau L)\cdot \cos (\tau L)\nonumber \\&\quad -\sin (\tau L)\cdot \cosh (\tau L)]. \end{aligned}$$

(24)