Time-optimal path planning in dynamic flows using level set equations: realistic applications

Abstract

The level set methodology for time-optimal path planning is employed to predict collision-free and fastest-time trajectories for swarms of underwater vehicles deployed in the Philippine Archipelago region. To simulate the multiscale ocean flows in this complex region, a data-assimilative primitive-equation ocean modeling system is employed with telescoping domains that are interconnected by implicit two-way nesting. These data-driven multiresolution simulations provide a realistic flow environment, including variable large-scale currents, strong jets, eddies, wind-driven currents, and tides. The properties and capabilities of the rigorous level set methodology are illustrated and assessed quantitatively for several vehicle types and mission scenarios. Feasibility studies of all-to-all broadcast missions, leading to minimal time transmission between source and receiver locations, are performed using a large number of vehicles. The results with gliders and faster propelled vehicles are compared. Reachability studies, i.e., determining the boundaries of regions that can be reached by vehicles for exploratory missions, are then exemplified and analyzed. Finally, the methodology is used to determine the optimal strategies for fastest-time pick up of deployed gliders by means of underway surface vessels or stationary platforms. The results highlight the complex effects of multiscale flows on the optimal paths, the need to utilize the ocean environment for more efficient autonomous missions, and the benefits of including ocean forecasts in the planning of time-optimal paths.

Appendix: Level set methodology for path planning

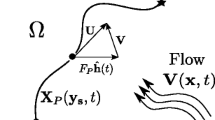
In this section, we briefly review the methodology and algorithm for time-optimal path planning used in this paper. The method has its roots in Lolla et al. (2012) and Lolla (2012). A formal proof and detailed algorithm are provided in the companion paper (Lolla et al. 2014). Let ${\Omega } \subseteq \mathbb {R}^{2}$ be an open set and let F>0. Suppose a vehicle (denoted by P) moves in Ω under the influence of a bounded, Lipschitz continuous dynamic flow field $\mathbf {V}(\mathbf {x},t):{\Omega } \times [0,\infty ) \rightarrow \mathbb {R}^{2}$. Let its start point and end point be y _s and y _f respectively, with y _s ,y _f ∈Ω. The vehicle’s trajectory, denoted by X _P (y _s ,t) follows the kinematic relation

$$ \frac{\text{d} \mathbf{X}_{P}}{\text{d} t} = F_{P}(t) \, \hat{\mathbf{h}}(t) + \mathbf{V}(\mathbf{X}_{P}(\mathbf{y}_{s},t) )\, , \quad {t > 0}\, , $$

(1)

where F _P (t)∈[0,F] is the nominal speed of the vehicle relative to the flow and $\hat {\mathbf {h}}(t)$ is the unit vector in the steering (heading) direction. The limiting conditions on X _P (y _s ,t) are

$$ \mathbf{X}_{P}(\mathbf{y}_{s},0) = \mathbf{y}_{s} \, ,\quad \mathbf{X}_{P}(\mathbf{y}_{s},\widetilde{T}(\mathbf{y}_{f})) = \mathbf{y}_{f} \, , $$

(2)

where $\widetilde {T}(\mathbf {y}): {\Omega } \rightarrow \mathbb {R}$ is the first “arrival time” at point y, i.e., the first time P reaches y. In this paper, it is assumed that V(x,t) is completely known. This may correspond to the mean or the mode of the forecast flow field given by an ocean modeling system (Lermusiaux et al. 2006; Haley and Lermusiaux 2010; Ueckermann et al. 2013). Furthermore, a kinematic model (1) for the interaction between the flow and the vehicle is assumed to be adequate. This assumption is reasonable for sufficiently long distance underwater path planning. In addition, the notation |∙| denotes the l–2 norm of ∙. F _P (t) and $\hat {\mathbf {h}}(t)$ together constitute the (isotropic) controls of the vehicle. For a general end point y∈Ω, let $F_{P}^{o}(t)$ and $\hat {\mathbf {h}}^{o}(t)$ be the corresponding optimal controls, i.e., controls that minimize $\widetilde {T}(\mathbf {y})$ subject to the constraints (1)–(2). Let this minimum arrival time be denoted by T ^o(y), and the resultant optimal trajectory be $\mathbf {X}^{o}_{P}(\mathbf {y}_{s},t)$. For the specific end point y _f ∈Ω, the superscript “ o” on quantities specific to the optimal trajectory is replaced by “ ⋆”.

1.1 A.1 Methodology

The path planning methodology described in Lolla et al. (2012) and (2014) involves computing the reachable set from a given starting point. The reachable set at any time t≥0, denoted by $\mathcal {R}(\mathbf {y}_{s},t)$, is defined as the set of all points y∈Ω for which there exist controls F _P (τ) and $\hat {\mathbf {h}}(\tau )$ for 0≤τ≤t and a resultant trajectory $\widetilde {\mathbf {X}}_{P}(\mathbf {y}_{s},\tau )$ satisfying Eq. 1 such that $\widetilde {\mathbf {X}}_{P}(\mathbf {y}_{s},t) = \mathbf {y}$. Hence, $\mathcal {R}(\mathbf {y}_{s},t)$ includes only those points which can be visited by the vehicle at time t. The boundary of the reachable set is called the reachability front and is denoted by $\partial \mathcal {R}(\mathbf {y}_{s},t)$. As a result, for any y∈Ω, T ^o(y) is the first time the reachability front $\partial \mathcal {R}(\mathbf {y}_{s},t)$ reaches y.

We showed in Lolla et al. (2014) that the reachable set $\mathcal {R}(\mathbf {y}_{s},t)$ is related to $\phi ^{o}:{\Omega } \times [0,\infty ) \rightarrow \mathbb {R}$, the viscosity solution of the Hamilton–Jacobi equation. Specifically, at any given time t≥0,

$$ \mathbf{x} \in \mathcal{R}(\mathbf{y}_{s},t) \iff \phi^{o}(\mathbf{x},t) \le 0 \, . $$

(3)

Equation 3 implies that the zero level set of ϕ ^o coincides with the reachability front $\partial \mathcal {R}(\mathbf {y}_{s},t)$ for any t≥0. This relationship between reachability and level sets of ϕ ^o enables an implicit computation of $\mathcal {R}(\mathbf {y}_{s},t)$ by numerically solving Eqs. 6–7.

In addition to the optimal arrival time T ^o(y), ϕ ^o also yields the optimal controls $F_{P}^{o}(t)$, $\hat {\mathbf {h}}^{o}(t)$ and trajectory $\mathbf {X}^{o}_{P}(\mathbf {y}_{s},t)$ leading to y. We showed in Lolla et al. (2014) that $\phi ^{o}(\mathbf {X}^{o}_{P}(\mathbf {y}_{s},t),t) = 0$ for all 0≤t≤T ^o(y), i.e., vehicles on optimal trajectories always remain on the zero level set of ϕ ^o. The optimal controls, for 0<t<T ^o(y) are

$$ F_{P}^{o}(t) = F \, , \quad \hat{\mathbf{h}}^{o}(t) = \frac{\nabla \phi^{o}(\mathbf{X}^{o}_{P}(\mathbf{y}_{s},t),t)}{| \nabla \phi^{o}(\mathbf{X}^{o}_{P}(\mathbf{y}_{s},t),t) |} \, , $$

(4)

whenever all the terms are well defined. Equivalently, if ϕ ^o is differentiable at $(\mathbf {X}^{o}_{P}(\mathbf {y}_{s},t),t)$ for some t∈(0,T ^o(y)), then,

$$ \frac{\text{d} \mathbf{X}^{o}_{P}}{\text{d} t} = F \, \frac{\nabla \phi^{o}(\mathbf{X}^{o}_{P}(\mathbf{y}_{s},t),t)}{| \nabla \phi^{o}(\mathbf{X}^{o}_{P}(\mathbf{y}_{s},t),t) |} + \mathbf{V}(\mathbf{X}^{o}_{P}(\mathbf{y}_{s},t),t)\, , $$

(5)

i.e., the optimal steering direction is normal to level sets of ϕ ^o, and the optimal relative speed of the vehicle is F.

1.2 A.2 Algorithm

The above discussion leads to an algorithm for minimum time path planning, given: y _s ,y _f ,F,V(x,t). The algorithm comprises of the following two steps.

• 1. Forward propagation. First, the reachability front $\partial \mathcal {R}(\mathbf {y}_{s},t)$ is evolved by solving the Hamilton–Jacobi Eq. 6 forward in time, with initial conditions (7). The front is evolved until it reaches y _f .

  $$ \frac{\partial \phi^{o}}{\partial t} + F | \nabla \phi^{o} | + \mathbf{V}(\mathbf{x},t) \cdot \nabla \phi^{o} = 0~~\text{in}~~{\Omega} \times (0,\infty) \, , $$

  (6)

  with initial conditions

  $$ \phi^{o}(\mathbf{x},0) = | \mathbf{x} - \mathbf{y}_{s} | \, , \quad \mathbf{x} \in {\Omega} \, . $$

  (7)

• 2. Backward vehicle tracking. After the front reaches y _f , the optimal vehicle trajectory $\mathbf {X}^{\star }_{P}(\mathbf {y}_{s},t)$ and controls are computed by solving Eq. 5 backward in time, starting from y _f at time T ^⋆(y _f )=T ^o(y _f ), i.e.,

  $$\begin{array}{@{}rcl@{}}&\frac{\text{d} \mathbf{X}^{\star}_{P}(\mathbf{y}_{s},t)}{\text{d} t} = - F \frac{\nabla \phi^{o}(\mathbf{X}_{P}^{\star},t)}{| \nabla \phi^{o}(\mathbf{X}_{P}^{\star},t) |}- \mathbf{V}(\mathbf{X}_{P}^{\star},t)\, , \\ &\text{with} \quad \mathbf{X}^{\star}_{P}(\mathbf{y}_{s},{T}^{\star}(\mathbf{y}_{f}) )= \mathbf{y}_{f} \, .\end{array} $$

  (8)

The backtracking step is necessary in this algorithm since the initial heading direction, $\hat {\mathbf {h}}^{o}(0)$ is not known a priori. In Lolla et al. (2012) and (2014) , a level set method is used to solve the Hamilton–Jacobi Eq. 6. As a result, efficient schemes such as the narrow-band method (Adalsteinsson and Sethian 1995) can be employed in the numerical scheme. Moreover, level set methods are well-known to offer substantial advantages over front tracking or other particle-based approaches (Sethian 1999; Osher and Fedkiw 2003). A thorough introduction to level set methods may be found in Lolla (2012). Numerical schemes used to solve Eqs. 6–8 are outlined in Lolla et al. (2014).