Skip to main content
SpringerLink
Log in

Linear programming using limited-precision oracles

  • Full Length Paper
  • Series B
  • Published:
Mathematical Programming Submit manuscript

Abstract

Since the elimination algorithm of Fourier and Motzkin, many different methods have been developed for solving linear programs. When analyzing the time complexity of LP algorithms, it is typically either assumed that calculations are performed exactly and bounds are derived on the number of elementary arithmetic operations necessary, or the cost of all arithmetic operations is considered through a bit-complexity analysis. Yet in practice, implementations typically use limited-precision arithmetic. In this paper we introduce the idea of a limited-precision LP oracle and study how such an oracle could be used within a larger framework to compute exact precision solutions to LPs. Under mild assumptions, it is shown that a polynomial number of calls to such an oracle and a polynomial number of bit operations, is sufficient to compute an exact solution to an LP. This work provides a foundation for understanding and analyzing the behavior of the methods that are currently most effective in practice for solving LPs exactly.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. Otherwise, as noted in [16], an oracle that guarantees a solution with residual errors bounded by a fixed constant could be queried for solutions of arbitrarily high precision in a single call by first scaling the problem data by a large constant. As we will see, this type of manipulation is not used by our algorithms. Moreover, the requirement in the definition of the oracle that the input data entries are in the bounded set \(\mathbb {F}(p)\) would forbid the input of arbitrarily scaled LPs.

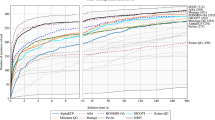
  2. In order to account fairly for small arbitrary deviations in time measurements, an algorithm is considered “fastest” if it solves an instance in no more than 5% of the time taken by the fastest method. Hence, the numbers do not add up to the total of 1202 instances. Furthermore, note that the same picture holds also when excluding easy instances that took less than 2 s by all solvers: SoPlex\(_{\text {fac}}\) wins more than twice as often as QSopt_ex.

  3. On three instances, floating-point SoPlex could not solve the first refinement LP within the time limit. For three further instances, the initial floating-point solve incorrectly claimed unboundedness and for one instance it incorrectly claimed infeasibility; in all of these cases, the incorrect claims were rejected successfully using feasibility and unboundedness tests as described in [16], but after starting to refine the original LP again, floating-point SoPlex  failed to return an approximately optimal solution even when trying to run with different floating-point settings.

References

  1. Abbott, J., Mulders, T.: How tight is Hadamard’s bound? Exp. Math. 10(3), 331–336 (2001). http://projecteuclid.org/euclid.em/1069786341

  2. Applegate, D.L., Cook, W., Dash, S., Espinoza, D.G.: QSopt_ex. http://www.dii.uchile.cl/~daespino/ESolver_doc/

  3. Applegate, D.L., Cook, W., Dash, S., Espinoza, D.G.: Exact solutions to linear programming problems. Oper. Res. Lett. 35(6), 693–699 (2007). https://doi.org/10.1016/j.orl.2006.12.010

    Article  MathSciNet  MATH  Google Scholar 

  4. Azulay, D.O., Pique, J.F.: Optimized \(Q\)-pivot for exact linear solvers. In: Maher, M., Puget, J.F. (eds.) Principles and Practice of Constraint Programming—CP98. Lecture Notes in Computer Science, vol. 1520, pp. 55–71. Springer, Berlin (1998). https://doi.org/10.1007/3-540-49481-2_6

    Chapter  Google Scholar 

  5. Chen, Z., Storjohann, A.: A BLAS based C library for exact linear algebra on integer matrices. In: Proceedings of the 2005 International Symposium on Symbolic and Algebraic Computation, ISSAC ’05, pp. 92–99 (2005). https://doi.org/10.1145/1073884.1073899

  6. Cheung, D., Cucker, F.: Solving linear programs with finite precision: II. Algorithms. J. Complex. 22(3), 305–335 (2006). https://doi.org/10.1016/j.jco.2005.10.001. http://www.sciencedirect.com/science/article/pii/S0885064X05000956

  7. Computational Optimization Research at Lehigh: MIP Instances. http://coral.ie.lehigh.edu/data-sets/mixed-integer-instances/

  8. Cook, W., Steffy, D.E.: Solving very sparse rational systems of equations. ACM Trans. Math. Softw. 37(4), 1–39 (2011). https://doi.org/10.1145/1916461.1916463

    Article  MathSciNet  MATH  Google Scholar 

  9. Dhiflaoui, M., Funke, S., Kwappik, C., Mehlhorn, K., Seel, M., Schömer, E., Schulte, R., Weber, D.: Certifying and repairing solutions to large LPs: How good are LP-solvers? In: Proceedings of the 14th Annual ACM-SIAM Symposium on Discrete Algorithms, SODA ’03, SIAM, pp. 255–256 (2003)

  10. Edmonds, J.: Systems of distinct representatives and linear algebra. J. Res. Natl. Bur. Stand. 71B(4), 241–245 (1967)

    Article  MathSciNet  Google Scholar 

  11. Edmonds, J., Maurras, J.F.: Note sur les \(Q\)-matrices d’Edmonds. RAIRO. Recherche Opérationnelle 31(2), 203–209 (1997). http://www.numdam.org/item?id=RO_1997__31_2_203_0

  12. Escobedo, A.R., Moreno-Centeno, E.: Roundoff-error-free algorithms for solving linear systems via Cholesky and LU factorizations. INFORMS J. Comput. 27(4), 677–689 (2015). https://doi.org/10.1287/ijoc.2015.0653

    Article  MathSciNet  MATH  Google Scholar 

  13. Escobedo, A.R., Moreno-Centeno, E.: Roundoff-error-free basis updates of LU factorizations for the efficient validation of optimality certificates. SIAM J. Matrix Anal. Appl. 38(3), 829–853 (2017). https://doi.org/10.1137/16M1089630

    Article  MathSciNet  MATH  Google Scholar 

  14. Espinoza, D.G.: On linear programming, integer programming and cutting planes. Ph.D. Thesis, Georgia Institute of Technology (2006). http://hdl.handle.net/1853/10482

  15. Gärtner, B.: Exact arithmetic at low cost—a case study in linear programming. Comput. Geom. 13(2), 121–139 (1999). https://doi.org/10.1016/S0925-7721(99)00012-7

    Article  MathSciNet  MATH  Google Scholar 

  16. Gleixner, A.M., Steffy, D.E., Wolter, K.: Iterative refinement for linear programming. INFORMS J. Comput. 28(3), 449–464 (2016). https://doi.org/10.1287/ijoc.2016.0692

    Article  MathSciNet  MATH  Google Scholar 

  17. Grötschel, M., Lovász, L., Schrijver, A.: Geometric Algorithms and Combinatorial Optimization, Algorithms and Combinatorics, vol. 2. Springer, Berlin (1988)

    Book  Google Scholar 

  18. Karmarkar, N.: A new polynomial-time algorithm for linear programming. Combinatorica 4(4), 373–395 (1984). https://doi.org/10.1007/BF02579150

    Article  MathSciNet  MATH  Google Scholar 

  19. Khachiyan, L.G.: Polynomial algorithms in linear programming (in Russian). Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki 20(1), 51–68 [English translation: USSR Computational Mathematics and Mathematical Physics, 20(1):53–72, 1980] (1980). https://doi.org/10.1016/0041-5553(80)90061-0

  20. Koch, T.: The final NETLIB-LP results. Oper. Res. Lett. 32(2), 138–142 (2004). https://doi.org/10.1016/S0167-6377(03)00094-4

    Article  MathSciNet  MATH  Google Scholar 

  21. Kwappik, C.: Exact linear programming. Master’s Thesis, Universität des Saarlandes (1998)

  22. Lenstra, A.K., Lenstra, H.W., Lovász, L.: Factoring polynomials with rational coefficients. Math. Ann. 261(4), 515–534 (1982). https://doi.org/10.1007/BF01457454

    Article  MathSciNet  MATH  Google Scholar 

  23. Mészáros, C.: LP test set. http://www.sztaki.hu/~meszaros/public_ftp/lptestset/

  24. Mittelmann, H.: LP test set. http://plato.asu.edu/ftp/lptestset/

  25. Nguyen, P.Q., Stehlé, D.: An LLL algorithm with quadratic complexity. SIAM J. Comput. 39(3), 874–903 (2009). https://doi.org/10.1137/070705702

    Article  MathSciNet  MATH  Google Scholar 

  26. Renegar, J.: A polynomial-time algorithm based on Newton’s method, for linear programming. Math. Program. 40(1–3), 59–93 (1988). https://doi.org/10.1007/BF01580724

    Article  MathSciNet  MATH  Google Scholar 

  27. Schrijver, A.: Theory of Linear and Integer Programming. Wiley, New York (1986)

    MATH  Google Scholar 

  28. Steffy, D.E.: Exact solutions to linear systems of equations using output sensitive lifting. ACM Commun. Comput. Algebra 44(3/4), 160–182 (2011). https://doi.org/10.1145/1940475.1940513

    Article  MATH  Google Scholar 

  29. University of Tennessee Knoxville and Oak Ridge National Laboratory: Netlib LP Library. http://www.netlib.org/lp/

  30. Wang, X., Pan, V.Y.: Acceleration of euclidean algorithm and rational number reconstruction. SIAM J. Comput. 2(32), 548–556 (2003)

    Article  MathSciNet  Google Scholar 

  31. Zuse Institute Berlin: MIPLIB—Mixed Integer Problem Library. http://miplib.zib.de/

  32. Zuse Institute Berlin: SoPlex. Sequential object-oriented simPlex. http://soplex.zib.de/

Download references

Acknowledgements

The authors would like to thank the anonymous reviewers for their detailed study of the manuscript and their comments, which were of exceptionally high quality.

Author information

Authors and Affiliations

  1. Konrad-Zuse-Zentrum für Informationstechnik Berlin, Takustr. 7, 14195, Berlin, Germany

    Ambros Gleixner

  2. Mathematics and Statistics, Oakland University, Rochester, Michigan, 48309, USA

    Daniel E. Steffy

Authors
  1. Ambros Gleixner
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Daniel E. Steffy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Daniel E. Steffy.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

An extended abstract of this work appeared as: Gleixner A., Steffy D.E. (2019) Linear Programming Using Limited-Precision Oracles. In: Lodi A., Nagarajan V. (eds) Integer Programming and Combinatorial Optimization. IPCO 2019. Lecture Notes in Computer Science, vol 11480. Springer, Cham.

Ambros Gleixner was supported by the Research Campus MODAL Mathematical Optimization and Data Analysis Laboratories funded by the German Ministry of Education and Research (BMBF Grant Number 05M14ZAM).

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 143 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gleixner, A., Steffy, D.E. Linear programming using limited-precision oracles. Math. Program. 183, 525–554 (2020). https://doi.org/10.1007/s10107-019-01444-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-019-01444-6

Keywords

Mathematics Subject Classification

Search

Navigation