Experimental study on hydraulic fracturing properties of elliptical boreholes

Abstract

Subsurface rocks are in the in situ stress state prior to drilling. The original and intact borehole subjected to stress redistribution can be deformed during field operations, and elliptical boreholes will be generated. Most laboratory scale hydraulic fracturing experimental specimens were predrilled in the center without considering lateral and axial pressure. In order to investigate the hydraulic fracturing characteristics of boreholes with non-circular appearance commonly seen in the field, hydraulic fracturing experiments were performed on boreholes with elliptical morphology. These experiments provide a comparison of elliptical and circular boreholes, and indicated that the horizontal in situ stress difference and borehole shape affect the breakdown pressure together. When the horizontal stress difference exists, the breakdown pressure reduces with the increase of the short-axis of elliptical boreholes. At zero horizontal stress difference, the situation is just the opposite. The analytic solutions of the stress fields near the elliptical borehole were obtained by employing the complex variable function. The fracture initiation conforms to the maximum tensile stress criterion. Whether the borehole is elliptical or circular, the damage process during hydraulic fracturing will cause fractures to eventually curve to the major stress direction.

Appendices

Appendix A

Derivation of stress field near elliptical boreholes

Basic assumptions

• 1. The target formation is isotropic, continuous, homogeneous, and elastic body. The sandstone which is more suitable for the above characteristics is selected in the experiment (Fig. 6).

• 2. The analytical solution of the stress field near the borehole under the action of far-field stress is simplified to solve the plane strain problem.

• 3. The body force of target formation is constant. For laboratory-scale tests, the mechanical effect of in situ stress and borehole hydraulic pressure on the specimen is far greater than that of the body force, so that the body force can be neglected.

Boundary conditions

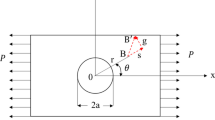
As shown in Fig. 7, the stress boundary for elliptical borehole is as follows:

$${\sigma }_{1}=-{q}_{1}$$

(9)

$${\sigma }_{2}=-{q}_{2}$$

(10)

The real constants related to the far-field stress are

$$B=\frac{{\sigma }_{1}+{\sigma }_{2}}{4}=-\frac{{q}_{1}+{q}_{2}}{4}$$

(11)

$${B}^{^{\prime}}+i{C}^{^{\prime}}=-\frac{1}{2}\left({\sigma }_{1}-{\sigma }_{2}\right){e}^{-2i\alpha }=-\frac{1}{2}\left({q}_{2}-{q}_{1}\right){e}^{-2i\alpha }$$

(12)

where B, ${B}^{^{\prime}}$, and ${C}^{^{\prime}}$ are given real constants characterizing the remote stress field. B is proportional to the sum of the two principal stresses at infinity in the elastic body, and ${B}^{^{\prime}}+i{C}^{^{\prime}}$ is proportional to the difference of the two principal stresses at infinity in the elastic body (MPa). σ₁ and σ₂ are principal stresses parallel to the cross section of the borehole (MPa). It is helpful to consider the magnitudes of σ₁ and σ₂ at depths in terms of σ_H and σ_h (or σ_H and σ_V, σ_h, and σ_V). The sign convention for stresses in elasticity is utilized in which tensile stress is positive and compressive one is negative. q₁ and q₂ refer to the magnitudes of the in situ stress (MPa).

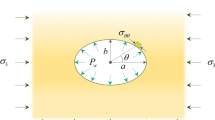
Due to the effect of fluid pressure in the borehole, taking the micro-unit at the boundary of the elliptical borehole as the objective to obtain the surface force as follows:

$$\overline{X }=-{q}_{3}\mathrm{cos}\left(N,x\right)=-{q}_{3}l$$

(13)

$$\overline{Y }=-{q}_{3}\mathrm{cos}\left(N,y\right)=-{q}_{3}m$$

(14)

where $\overline{X }$ and $\overline{Y }$ are surface forces of the micro-unit at the boundary of the elliptical borehole, that is the principal vector of the surface force between the base point A and any point B on the s-boundary (Fig. 18) (MPa). l and m are the direction cosine of the outward normal at the boundary. q₃ is the magnitude of the fluid pressure (MPa).

We obtain the micro-unit’s surface force on the complex plane as follows:

$$\overline{X }+i\overline{Y }=-{q}_{3}\left(l+im\right)$$

(15)

$$\left(\overline{X }+i\overline{Y }\right)ds=-{q}_{3}\left(l+im\right)ds=-{q}_{3}\left(dy-idx\right)=i{q}_{3}\left(dx+idy\right)=i{q}_{3}dz$$

(16)

where ds is the length of the micro-unit at the boundary. dz are complex numbers.

Since the fluid pressure is equal at any point on the wall of the borehole, the surface force acting on the wall of the elliptical borehole becomes an equilibrium system, so the principal vector of the surface force is X = Y = 0.

Fig. 18

Schematic diagram of the surface force action of the micro-unit of the borehole boundary

Theoretical derivation

For the orifice problem of various shapes, the region occupied by an object on one complex plane can be mapped to the interior or exterior of the central unit circle on another complex plane by conformal mapping. Following Muskhelishvili’s writings, introduce the following mapping function to simplify the geometry of the elliptical borehole as follows:

$$Z=\omega \left(\xi \right)=R\left(\frac{1}{\xi }+m\xi \right)$$

(17)

$$R=\frac{a+b}{2}$$

(18)

$$m=\frac{a-b}{a+b}$$

(19)

$$\xi =\rho \left(\cos\theta +i\sin\theta \right)$$

(20)

Equation (17) shows that the point z on the complex plane Z occupied by an ellipse is mapped to the interior of the central unit circle on complex plane ξ.

Where a and b are the semi-axes of the ellipse and 0 ≤ m ≤ 1. When m = 0, the ellipse becomes a circle, and in the limit m = 1, it becomes a crack. The mapping function transforms the exterior region of an ellipse into the interior region of a unit circle. θ is measured counterclockwise from x-axis direction and varies from 0 to 360°. This angle indicates the orientation of the stresses around the wellbore circumference. ρ is the distance between the point inside the unit circle and the center of the circle.

On the elliptical borehole wall, ρ = 1 for the unit circle, so Eqs. (20) and (17) are:

$$\xi =\sigma =\cos\theta +i\sin\theta$$

(21)

$$\omega \left(\sigma \right)=R\left(\frac{1}{\sigma }+m\sigma \right)$$

(22)

where σ is the point at which the elliptical boundary on the complex plane Z is mapped to the boundary of the central unit circle on the ξ-plane.

In the complex function solution, the notation f₀ is introduced for the convenience of calculation. The expression of f₀ is as follows:

$$\begin{aligned}{f}_{0}\text{=}&i\int \left(\overline{X }+i\overline{Y }\right)ds-\frac{X+iY}{2\pi }\mathrm{ln}\sigma -\frac{1+\mu }{8\pi }\left(X-iY\right)\frac{\omega \left(\sigma \right)}{\overline{{\omega }^{^{\prime}}\left(\sigma \right)}}\sigma \\&-2B\omega \left(\sigma \right)-\left({B}^{^{\prime}}-i{C}^{^{\prime}}\right)\stackrel{-}{\omega \left(\sigma \right)}\end{aligned}$$

(23)

Incorporating Eqs. (12), (16), and (22) into Eq. (23), we have the following:

$$\begin{aligned}{f}_{0}\text{=}&-{q}_{3}R\left(\frac{1}{\sigma }+m\sigma \right)+\frac{{q}_{1}+{q}_{2}}{2}R\left(\frac{1}{\sigma }+m\sigma \right)\\&+\frac{1}{2}\left({q}_{2}-{q}_{1}\right)R\left(\sigma +\frac{m}{\sigma }\right){e}^{2i\alpha }\end{aligned}$$

(24)

f₀ is related to the single valued analytic functions φ₀(ξ) inside the unit circle as follows:

$${\varphi }_{0}\left(\xi \right)\text{=}\frac{1}{2\pi i}{\int }_{\sigma }\frac{{f}_{0}}{\sigma -\xi }d\sigma$$

(25)

Incorporating Eq. (24) into Eq. (25) and using the Cauchy integral principle, we have the following:

$$\begin{array}{c}{\varphi }_{0}\left(\xi \right)\text{=}\frac{1}{2\pi i}{\int }_{\sigma }\left[-{q}_{3}R\left(\frac{1}{\sigma }+m\sigma \right)+\frac{{q}_{1}+{q}_{2}}{2}R\left(\frac{1}{\sigma }+m\sigma \right)+\frac{1}{2}\left({q}_{2}-{q}_{1}\right)R\left(\sigma +\frac{m}{\sigma }\right){e}^{2i\alpha }\right]\frac{d\sigma }{\sigma -\xi }\\ =-{q}_{3}Rm\xi +\frac{1}{2}\left({q}_{1}+{q}_{2}\right)Rm\xi +\frac{1}{2}\left({q}_{2}-{q}_{1}\right)R\xi {e}^{2i\alpha }\end{array}$$

(26)

$\overline{{f }_{0}}$ and ${\varphi }_{0}^{^{\prime}}\left(\xi \right)$ are related to the single valued analytic functions ψ₀(ξ) inside the unit circle as follows:

$${\psi }_{0}\left(\xi \right)\text{=}\frac{1}{2\pi i}{\int }_{\sigma }\frac{\overline{{f }_{0}}}{\sigma -\xi }d\sigma -\xi \frac{{\xi }^{2}+m}{m{\xi }^{2}-1}{\varphi }_{0}^{^{\prime}}\left(\xi \right)$$

(27)

In the same way, we have the following:

$$\begin{aligned}{\psi }_{0}\left(\xi \right)=&R\xi \left[\left(\frac{{q}_{1}+{q}_{2}}{2}-{q}_{3}\right)\left(1-m\frac{{\xi }^{2}+m}{m{\xi }^{2}-1}\right)\right.\\&\left.+\frac{{q}_{2}-{q}_{1}}{2}\left(m{e}^{-2i\alpha }-\frac{{\xi }^{2}+m}{m{\xi }^{2}-1}{e}^{2i\alpha }\right)\right]\end{aligned}$$

(28)

where $\overline{{f }_{0}}$ is the conjugate complex function of the f₀.

The expressions for the complex functions φ(ξ) and ψ(ξ) characterizing the airy stress function are as follows:

$$\varphi \left(\xi \right)=\frac{1+\mu }{8\pi }\left(X+iY\right)\mathrm{ln}\xi +B\omega \left(\xi \right)+{\varphi }_{0}\left(\xi \right)$$

(29)

$$\psi \left(\xi \right)=-\frac{3-\mu }{8\pi }\left(X-iY\right)\mathrm{ln}\xi +\left({B}^{^{\prime}}+i{C}^{^{\prime}}\right)\omega \left(\xi \right)+{\psi }_{0}\left(\xi \right)$$

(30)

where φ(ξ) and ψ(ξ) are the two analytical functions represented by the complex function ξ. They are used to characterize the stress function in the plane problem where the body force is constant.

Incorporating Eqs. (11), (17), and (26) into Eq. (29), we have the following:

$$\varphi \left(\xi \right)=Rm\xi \left(\frac{{q}_{1}+{q}_{2}}{4}-{q}_{3}\right)+\frac{{q}_{2}-{q}_{1}}{2}R\xi {e}^{2i\alpha }-\frac{{q}_{1}+{q}_{2}}{4}R\frac{1}{\xi }$$

(31)

Incorporating Eqs. (12), (17), and (28) into Eq. (30), we have the following:

$$\begin{aligned}\psi \left(\xi \right)=&R\xi \left[\left(\frac{{q}_{1}+{q}_{2}}{2}-{q}_{3}\right)\left(1-m\frac{{\xi }^{2}+m}{m{\xi }^{2}-1}\right)-\frac{{q}_{2}-{q}_{1}}{2}\frac{{\xi }^{2}+m}{m{\xi }^{2}-1}{e}^{2i\alpha }\right]\\&-\frac{{q}_{2}-{q}_{1}}{2}{e}^{-2i\alpha }\frac{R}{\xi }\end{aligned}$$

(32)

The relationship between φ(ξ) and ψ(ξ) and the stress field in the vicinity of the elliptical borehole is as follows:

$$\Phi \left(\xi \right)=\frac{{\varphi }^{^{\prime}}\left(\xi \right)}{{\omega }^{^{\prime}}\left(\xi \right)}$$

(33)

$$\Psi \left(\xi \right)=\frac{{\psi }^{^{\prime}}\left(\xi \right)}{{\omega }^{^{\prime}}\left(\xi \right)}$$

(34)

$${\sigma }_{\rho \rho }+{\sigma }_{\theta \theta }=4\mathrm{Re}\Phi \left(\xi \right)$$

(35)

$${\sigma }_{\theta \theta }-{\sigma }_{\rho \rho }+2i{\tau }_{\rho \theta }=\frac{2{\xi }^{2}}{{\rho }^{2}\overline{{\omega }^{^{\prime}}\left(\xi \right)}}\left[\stackrel{-}{\omega \left(\xi \right)}{\Phi }^{^{\prime}}\left(\xi \right)+{\omega }^{^{\prime}}\left(\xi \right)\Psi \left(\xi \right)\right]$$

(36)

where σ_ρρ is the radial stress (MPa), σ_θθ is the circumferential stress (MPa), τ_ρθ is the tangential shear stress (MPa). Φ(ξ) and Ψ(ξ) are the two analytical functions represented by the complex function ξ. Re refers to the real part of the complex function Φ(ξ).

Incorporating Eqs. (31) and (32) into Eqs. (33), (34), (35), and (36), we have the following:

$$\begin{array}{l}{\sigma }_{\theta \theta }=\frac{1}{2\left({m}^{2}-2m{\rho }^{-2}\cos 2\theta +{\rho }^{-4}\right)}\left\{\begin{array}{l}\left(m\cos 2\theta -{\rho }^{-2}\right)\frac{{\rho }^{-2}\left({q}_{1}+{q}_{2}\right)\left({\rho }^{-4}-{m}^{2}\cos 4\theta \right)}{{m}^{2}-2m{\rho }^{-2}\cos 2\theta +{\rho }^{-4}}-\frac{{m}^{3}{\rho }^{-2}\left({q}_{1}+{q}_{2}\right)\sin 4\theta \sin 2\theta }{{m}^{2}-2m{\rho }^{-2}\cos 2\theta +{\rho }^{-4}}\\ -4{\rho }^{-2}\left(m\cos 2\theta -{\rho }^{-2}\right)\frac{\left({\rho }^{-2}\cos 2\theta +m\cos 4\theta \right)\left(GE+HF\right)+\left(HE-GF\right)\left(m\sin 4\theta +{\rho }^{-2}\sin 2\theta \right)}{{E}^{2}+{F}^{2}}\\ +4m \sin 2\theta \frac{\left[\left({\rho }^{-4}\cos 2\theta +m{\rho }^{-2}\cos 4\theta \right)\left(HE-GF\right)-\left(m{\rho }^{-2}\sin 4\theta +{\rho }^{-4}\sin 2\theta \right)\left(GE+HF\right)\right]}{{E}^{2}+{F}^{2}}\\ +2\left(m\cos 2\theta -{\rho }^{-2}\right)\left(\frac{{q}_{1}+{q}_{2}}{2}-{q}_{3}\right)+{\rho }^{-2}\left({q}_{2}-{q}_{1}\right)\left[\left(m\cos 2\theta -{\rho }^{-2}\right)\cos \left(2\alpha +2\theta \right)+m\sin 2\theta \sin \left(2\alpha +2\theta \right)\right]\\ -2\frac{\left[N\left(m\cos 2\theta -{\rho }^{-2}\right)-\frac{{q}_{2}-{q}_{1}}{2}m\sin 2\theta \sin 2\alpha \right]\left(LJ+MK\right)-\left(MJ-LK\right)\left[\frac{{q}_{2}-{q}_{1}}{2}\sin 2\alpha \left(m\cos 2\theta -{\rho }^{-2}\right)+Nm\sin 2\theta \right]}{{J}^{2}+{K}^{2}}\end{array}\right\}\\ +2\frac{\left[m\left(\frac{{q}_{1}+{q}_{2}}{4}-{q}_{3}\right)+\frac{{q}_{2}-{q}_{1}}{2}\cos 2\alpha +\frac{{q}_{1}+{q}_{2}}{4{\rho }^{2}}\cos 2\theta \right]\left(m-{\rho }^{-2}\cos 2\theta \right)+{\rho }^{-2}\left(\frac{{q}_{2}-{q}_{1}}{2}\sin 2\alpha -\frac{{q}_{1}+{q}_{2}}{4{\rho }^{2}}\sin 2\theta \right)\sin 2\theta }{{m}^{2}-2m{\rho }^{-2}\cos 2\theta +{\rho }^{-4}}\end{array}$$

(37)

$$\begin{array}{l}{\sigma }_{\rho \rho }=2\frac{\left[m\left(\frac{{q}_{1}+{q}_{2}}{4}-{q}_{3}\right)+\frac{{q}_{2}-{q}_{1}}{2}\cos 2\alpha +\frac{{q}_{1}+{q}_{2}}{4{\rho }^{2}}\cos 2\theta \right]\left(m-{\rho }^{-2}\cos 2\theta \right)+{\rho }^{-2}\left(\frac{{q}_{2}-{q}_{1}}{2}\sin 2\alpha -\frac{{q}_{1}+{q}_{2}}{4{\rho }^{2}}\sin 2\theta \right)\sin 2\theta }{{m}^{2}-2m{\rho }^{-2}\cos 2\theta +{\rho }^{-4}}\\ -\frac{1}{2\left({m}^{2}-2m{\rho }^{-2}\cos 2\theta +{\rho }^{-4}\right)}\left\{\begin{array}{l}\left(m\cos 2\theta -{\rho }^{-2}\right)\frac{{\rho }^{-2}\left({q}_{1}+{q}_{2}\right)\left({\rho }^{-4}-{m}^{2}\cos 4\theta \right)}{{m}^{2}-2m{\rho }^{-2}\cos 2\theta +{\rho }^{-4}}-\frac{{m}^{3}{\rho }^{-2}\left({q}_{1}+{q}_{2}\right)\sin 4\theta \sin 2\theta }{{m}^{2}-2m{\rho }^{-2}\cos 2\theta +{\rho }^{-4}}\\ -4{\rho }^{-2}\left(m\cos 2\theta -{\rho }^{-2}\right)\frac{\left({\rho }^{-2}\cos 2\theta +m\cos 4\theta \right)\left(GE+HF\right)+\left(HE-GF\right)\left(m\sin 4\theta +{\rho }^{-2}\sin 2\theta \right)}{{E}^{2}+{F}^{2}}\\ +4m \sin 2\theta \frac{\left[\left({\rho }^{-4}\cos 2\theta +m{\rho }^{-2}\cos 4\theta \right)\left(HE-GF\right)-\left(m{\rho }^{-2}\sin 4\theta +{\rho }^{-4}\sin 2\theta \right)\left(GE+HF\right)\right]}{{E}^{2}+{F}^{2}}\\ +2\left(m\cos 2\theta -{\rho }^{-2}\right)\left(\frac{{q}_{1}+{q}_{2}}{2}-{q}_{3}\right)+{\rho }^{-2}\left({q}_{2}-{q}_{1}\right)\left[\left(m\cos 2\theta -{\rho }^{-2}\right)\cos \left(2\alpha +2\theta \right)+m\sin 2\theta \sin \left(2\alpha +2\theta \right)\right]\\ -2\frac{\left[N\left(m\cos 2\theta -{\rho }^{-2}\right)-\frac{{q}_{2}-{q}_{1}}{2}m\sin 2\theta \sin 2\alpha \right]\left(LJ+MK\right)-\left(MJ-LK\right)\left[\frac{{q}_{2}-{q}_{1}}{2}\sin 2\alpha \left(m\cos 2\theta -{\rho }^{-2}\right)+Nm\sin 2\theta \right]}{{J}^{2}+{K}^{2}}\end{array}\right\}\end{array}$$

(38)

$${\tau }_{\rho \theta }=\frac{1}{2\left({m}^{2}-2m{\rho }^{-2}\cos 2\theta +{\rho }^{-4}\right)}\left\{\begin{array}{l}+\frac{\left({q}_{1}+{q}_{2}\right)\left({\rho }^{-4}-{m}^{2}\cos 4\theta \right){\rho }^{-2}m\sin 2\theta }{{m}^{2}-2m{\rho }^{-2}\cos 2\theta +{\rho }^{-4}}+\frac{\left({q}_{1}+{q}_{2}\right)\left(m\cos 2\theta -{\rho }^{-2}\right){m}^{2}{\rho }^{-2}\sin 4\theta }{{m}^{2}-2m{\rho }^{-2}\cos 2\theta +{\rho }^{-4}}\\ -4m \sin 2\theta \frac{\left({\rho }^{-4}\cos 2\theta +m{\rho }^{-2}\cos 4\theta \right)\left(GE+HF\right)+\left(HE-GF\right)\left(m{\rho }^{-2}\sin 4\theta +{\rho }^{-4}\sin 2\theta \right)}{{E}^{2}+{F}^{2}}\\ -4\left(m\cos 2\theta -{\rho }^{-2}\right)\frac{\left[\left({\rho }^{-4}\cos 2\theta +m{\rho }^{-2}\cos 4\theta \right)\left(HE-GF\right)-\left(m{\rho }^{-2}\sin 4\theta +{\rho }^{-4}\sin 2\theta \right)\left(GE+HF\right)\right]}{{E}^{2}+{F}^{2}}\\ +2m\left(\frac{{q}_{1}+{q}_{2}}{2}-{q}_{3}\right)\sin 2\theta +2\frac{{q}_{2}-{q}_{1}}{2}{\rho }^{-2}m\sin 2\theta cos\left(2\alpha +2\theta \right)-2\left(m\cos 2\theta -{\rho }^{-2}\right)\frac{{q}_{2}-{q}_{1}}{2}{\rho }^{-2}\sin\left[\left(2\alpha +2\theta \right)\right]\\ -2\frac{\left[\frac{{q}_{2}-{q}_{1}}{2}\left(m\cos 2\theta -{\rho }^{-2}\right)\sin 2\alpha +Nm\sin 2\theta \right]\left(LJ+MK\right)+\left(MJ-LK\right)\left[N\left(m\cos 2\theta -{\rho }^{-2}\right)-\frac{{q}_{2}-{q}_{1}}{2}m\sin 2\theta \sin 2\alpha \right]}{{J}^{2}+{K}^{2}}\end{array}\right\}$$

(39)

where

$$\begin{array}{l}E={m}^{2}-2m{\rho }^{-2}\cos 2\theta +{\rho }^{-4}\cos4\theta ,F=2m{\rho }^{-2}\sin 2\theta -{\rho }^{-4}\sin 4\theta ,G=m\left(\frac{{q}_{1}+{q}_{2}}{4}-{q}_{3}\right)+\frac{{q}_{2}-{q}_{1}}{2}\cos 2\alpha +\frac{{q}_{1}+{q}_{2}}{4}{\rho }^{-2}\cos 2\theta \\ H=\frac{{q}_{2}-{q}_{1}}{2}\sin 2\alpha -\frac{{q}_{1}+{q}_{2}}{4}{\rho }^{-2}\sin 2\theta ,J={m}^{2}{\rho }^{4}\cos 4\theta -2m{\rho }^{2}\cos 2\theta +1,K={m}^{2}{\rho }^{4}\sin 4\theta -2m{\rho }^{2}\sin 2\theta \\ L=m{\rho }^{4}\cos 4\theta -\left({m}^{2}+3\right){\rho }^{2}\cos 2\theta -m,M=m{\rho }^{4}\sin 4\theta -\left({m}^{2}+3\right){\rho }^{2}\sin 2\theta ,N=m\left(\frac{{q}_{1}+{q}_{2}}{2}-{q}_{3}\right)+\frac{{q}_{2}-{q}_{1}}{2}\cos 2\alpha \end{array}$$

We obtain the analytical solutions of the stress field near the elliptical borehole under the action of far-field stress (–q₁ and –q₂) and internal borehole pressure (–q₃). According to Eqs. (37), (38), and (39), the radial stress (σ_ρρ), circumferential (or tangential or hoop) stress (σ_θθ), and tangential shear stress (τ_rθ) are functions of angles θ and α, in situ stress (–q₁ and –q₂), internal borehole pressure (–q₃) and shape parameter m. Therefore, any change in abovementioned parameters will affect the σ_ρρ, σ_θθ and τ_rθ.

However, the most important for us is the stress at the edge of the elliptical borehole, that is, ρ = 1. The above equations corresponding to the borehole wall (where ρ = 1) are simplified to

$$\left\{\begin{array}{l}{\sigma }_{\rho }=-{q}_{3}\\ {\sigma }_{\theta }=\frac{\left({q}_{1}+{q}_{2}\right)\left({m}^{2}-1\right)+2\left({q}_{2}-{q}_{1}\right)\left[m\cos 2\alpha -\cos 2\left(\alpha +\theta \right)\right]-4m{q}_{3}\left(m-\cos 2\theta \right)}{{\left(m-\cos 2\theta \right)}^{2}\text{+}{\sin }^{2}2\theta }+{q}_{3}\\ {\tau }_{\rho \theta }=0\end{array}\right.$$

(40)

Degenerate to the circular borehole/roadway

It is well known that analytical solutions for stress fields near circular boreholes/roadways are widely used in industrial fields, such as coal mines, petroleum, natural gas, and tunnels. Substituting m = 0, q₃ = 0 and α = π/2 into the Eqs. (31), (37) and (38) can degenerate into the classical analytical solution of the stress field near the circular borehole/roadway as follows:

$$\begin{aligned}{\sigma }_{\rho \rho }=&\frac{1}{2}\left[\left(-{q}_{1}\right)+\left(-{q}_{2}\right)\right]\left(1-{\rho }^{2}\right)+\frac{1}{2}\\&\left[\left(-{q}_{2}\right)-\left(-{q}_{1}\right)\right]\left(1-4{\rho }^{2}+3{\rho }^{4}\right)\cos 2\theta\end{aligned}$$

(41)

$$\begin{aligned}{\sigma }_{\theta \theta }=&\frac{1}{2}\left[\left(-{q}_{1}\right)+\left(-{q}_{2}\right)\right]\left(1+{\rho }^{2}\right)-\frac{1}{2}\left[\left(-{q}_{2}\right)-\left(-{q}_{1}\right)\right]\\&\left(1+3{\rho }^{4}\right)\cos 2\theta\end{aligned}$$

(42)

$${\tau }_{\rho \theta }=\frac{1}{2}\left[\left(-{q}_{2}\right)-\left(-{q}_{1}\right)\right]\left(1+2{\rho }^{2}-3{\rho }^{4}\right)\sin 2\theta$$

(43)

where $\rho =\frac{{R}_{0}}{r}$, R₀ is the radius of the borehole, r is distance from the center of the hole.

If the relevant parameters are known, the maximum circumferential stress of the elliptical borehole can be obtained by employing Eqs. (37), (38), and (39). According to the maximum tensile stress criterion, the variation trend of the breakdown pressure of the elliptical borehole with different shapes can be predicted.