Three-dimensional benchmark for variable-density flow and transport simulation: matching semi-analytic stability modes for steady unstable convection in an inclined porous box

Abstract

This benchmark for three-dimensional (3D) numerical simulators of variable-density groundwater flow and solute or energy transport consists of matching simulation results with the semi-analytical solution for the transition from one steady-state convective mode to another in a porous box. Previous experimental and analytical studies of natural convective flow in an inclined porous layer have shown that there are a variety of convective modes possible depending on system parameters, geometry and inclination. In particular, there is a well-defined transition from the helicoidal mode consisting of downslope longitudinal rolls superimposed upon an upslope unicellular roll to a mode consisting of purely an upslope unicellular roll. Three-dimensional benchmarks for variable-density simulators are currently (2009) lacking and comparison of simulation results with this transition locus provides an unambiguous means to test the ability of such simulators to represent steady-state unstable 3D variable-density physics.

Résumé

Ce banc d′essai pour simulation numérique tridimensionnelle (3D) d′un flot d′écoulement souterrain de densité ou d′énergie variable permet de comparer les résultats semi-analytiques de transition d′un mode convectif en régime permanent à un autre, dans une boîte poreuse. Des études expérimentales et analytiques antérieures de flux convectif libre dans un milieu poreux incliné ont montré qu′il existe différents modes de convection possibles dépendant des paramètres du système, géométrie et inclinaison. En particulier, il existe une transition nette entre le mode hélicoïdal, consistant en écoulements longitudinaux descendants surimposés à un flux unicellulaire ascendant et un mode d′écoulement unicellulaire purement ascendant. Des bancs d′essai tri-dimensionnels pour simulations d′écoulements de densité variable manquent actuellement (2009) et la comparaison de simulations avec ce dispositif de transition montre clairement la capacité de tels simulateurs à représenter en 3 dimensions la physique des phénomènes instables en régime permanent.

Resumen

Este estándar de comparación para simuladores numéricos tridimensionales (3D) de flujo de agua subterránea de densidad variable y transporte de solutos o energía consiste en comparar los resultados de la simulación con la solución semianalítica para la transición de un modo convectivo de estado estacionario a otro de una capa porosa. Experimentos previos y estudios analíticos de flujo convectivo natural en una capa porosa inclinada han demostrado que hay una variedad de posibles modos convectivos dependiendo en los parámetros del sistema, la geometría y la inclinación. En particular, existe una transición bien definida desde el modo helicoidal que consiste en rollos inclinados pendiente abajo superpuestos por sobre un rollo unicelular pendiente arriba a un modo que consiste en un rollo unicelular puro y pendiente arriba. Se carece actualmente (2009) de estándar de comparación tridimensionales para simuladores de densidad variable y la comparación de los resultados de simulaciones con este lugar de transición proporciona un medio inambiguo para testear la habilidad de tales simuladores para representar la física del estado estacionario inestable de densidad variable en 3D.

摘要

这一变密度地下水流和溶质或能量运移的三维数值模拟基准由多孔介质自一个稳态对流模式向另一个稳态对流模式转变的半解析解匹配仿真结果 组成。已有对天然条件下倾斜多孔介质层中对流的实验和解析研究表明, 有很多取决于系统参数、几何形状和倾角的对流模式。特别是由下斜的纵向卷叠加上斜单卷的螺旋式模型到仅仅包括上斜单卷模式的转换, 研究较为清楚。目前 (2009) 缺少变密度流模拟的三维基准, 且模拟结果与这种转换点的比较为检验这种模拟器代表稳态的非稳定3D变密度物理机制的能力提供了确定的方法。

Resumo

Este teste de referência (benchmark) para simuladores numéricos tridimensionais (3D) de fluxo de água subterrânea de densidade variável e transporte de soluto ou energia consiste em ajustar os resultados da simulação com a solução semi-analítica para a transição de um modo convectivo estacionário para um outro numa caixa porosa. Os estudos experimentais e analíticos anteriores do fluxo convectivo natural numa camada porosa inclinada mostraram que existe uma variedade de modos convectivos possíveis dependendo dos parâmetros do sistema, da geometria e da inclinação. Em particular, há uma transição bem definida do modo helicoidal consistindo de cilindros longitudinais descendentes sobrepostos a um cilindro unicelular ascendente em relação a um modo consistindo num cilindro unicelular ascendente. Actualmente (2009) há uma falta de testes de referência tridimensionais para simuladores de densidade variável e a comparação dos resultados da simulação com este ponto de transição dá um meio inequívoco para testar a capacidade de tais simuladores representarem a física de densidade variável a 3D, instável e estacionária.

Appendix: Details of calculating Rayleigh numbers with Galerkin′s method

The purpose of this appendix is to elaborate on details of the Galerkin solution method used by Caltagirone and Bories (1985) (designated CB) that are either not immediately obvious or are considered erroneous in their paper. It is expected that the paper of CB should be read concurrently. CB set up model equations for thermal instability in an inclined porous layer in terms of temperature T. Mathematically equivalent equations are used here with concentration, C, replacing T. Much of the symbolism used by CB is used here for easy comparison.

The basic 3D equations are

$$ \nabla \cdot V = 0 $$

(3)

$$ - \nabla p + R_a^* kC - V = 0 $$

(4)

$$ \frac{{\partial C}}{{\partial t}} - {\nabla ^2}C + V \cdot \nabla C = 0 $$

(5)

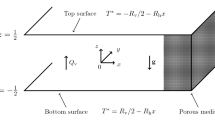
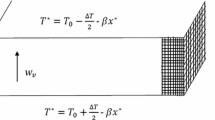
with vectors V = {U,V,W}, ∇ = {∂ _x, ∂ _y ,∂ _x} and k = {sinϕ,0,cosϕ} for a Cartesian (x,y,z) system. U, V, W are velocities corresponding to coordinates x, y, z, respectively, t is time and z is restricted to the range 0 ≤ z ≤ 1 as shown in Fig. 1. Also

$$ {\nabla^2} = \partial_x^2 + \partial_y^2 + \partial_z^2 $$

(6)

The Rayleigh number $R_a^*$ is identical to Ra defined by Eq. 1.

Stability of flow in an infinite-extension layer

For an inclined layer of infinite extensions in x- and y-directions a solution of the Eqs. (3)–(5) corresponding to unicellular flow provides concentration and velocity fields:

$$ {C_0} = 1 - z;\quad {U_0} = \left( {\frac{1}{2} - z} \right)R_a^* \sin \phi; \quad {V_0} = 0;\quad {W_0} = 0 $$

(7)

Equations of perturbation ({θ,w}:{C,W}) relative to this flow follow from Eqs. (3)–(5) as

$$ {\nabla^2}\theta - R_a^* \left( {\frac{1}{2} - z} \right)\sin \phi \frac{{\partial \theta }}{{\partial x}} + w = \frac{{\partial \theta }}{{\partial t}} $$

(8)

$$ {\nabla^2}w + R_a^* \left[ {\sin \phi \frac{{{\partial^2}\theta }}{{\partial x\partial z}} - \cos \phi \left( {\frac{{{\partial^2}\theta }}{{\partial {x^2}}} + \frac{{{\partial^2}\theta }}{{\partial {y^2}}}} \right)} \right] = 0 $$

(9)

Eliminate w from Eqs. (8) and (9) by taking ∇² of Eq. (8) then substituting ∇² w from Eq. (9):

$$ \left\{ {{\nabla^4} - R_a^* \sin \phi {\nabla^2}\left( {\frac{1}{2} - z} \right) - R_a^* \left[ {\sin \phi {\partial_x}{\partial_z} - \cos \phi \left( {\partial_x^2 + \partial_y^2} \right)} \right] - {\nabla^2}{\partial_t}} \right\}\theta = 0 $$

(10)

Noting

$$ - {\nabla^2}\left[ {\left( {\frac{1}{2} - z} \right)\theta } \right] = \left( {z - \frac{1}{2}} \right){\nabla^2}\theta + 2\frac{{\partial \theta }}{{\partial z}} $$

(11)

and letting

$$ \begin{array}{*{20}{c}} {\theta = \psi (z){e^{\left( {\sigma t + i{s_x}x + i{s_y}y} \right)}} = \psi E} \hfill \\ {{s^2} = s_x^2 + s_y^2,\quad i = \sqrt {{ - 1}} } \hfill \\ \end{array} $$

(12)

then

$$ \begin{array}{*{20}{c}} {{\nabla^2}\theta = \left( {\frac{{{\partial^2}\psi }}{{\partial {z^2}}} - {s^2}\psi } \right)E,\quad {\nabla^4}\theta = {{\left( {\frac{{{\partial^2}}}{{\partial {z^2}}} - {s^2}} \right)}^2}\psi E} \hfill \\ {\frac{{{\partial^2}\theta }}{{\partial x\partial z}} = i{s_x}\frac{{\partial \psi }}{{\partial z}}E,\quad \frac{{\partial \theta }}{{\partial t}} = \sigma \psi E} \hfill \\ \end{array} $$

(13)

Substituting these derivatives in Eq. (10) produces

$$ \begin{array}{*{20}{c}} \hfill {\left[ {{{\left( {\frac{{{\partial^2}}}{{\partial {z^2}}} - {s^2}} \right)}^2} - {s^2}R_a^* \cos \phi } \right]\psi + i{s_x}R_a^* \sin \phi \left[ {\left( {z - \frac{1}{2}} \right)\left( {\frac{{{\partial^2}}}{{\partial {z^2}}} - {s^2}} \right)\psi + \frac{{\partial \psi }}{{\partial z}}} \right]} \\ \hfill { - \sigma \left( {\frac{{{\partial^2}}}{{\partial {z^2}}} - {s^2}} \right)\psi = 0} \\ \end{array} $$

(14)

Marginal stability requires σ = 0. Then Eq. (14) becomes

$$ \begin{array}{*{20}{c}} {{L_{40}}\left[ \psi \right] = } \hfill \\ {\left[ {{{\left( {\frac{{{\partial^2}}}{{\partial {z^2}}} - {s^2}} \right)}^2} - {s^2}R_a^* \cos \phi } \right]\psi + i{s_x}R_a^* \sin \phi \left[ {\left( {z - \frac{1}{2}} \right)\left( {\frac{{{\partial^2}}}{{\partial {z^2}}} - {s^2}} \right)\psi + \frac{{\partial \psi }}{{\partial z}}} \right] = 0} \hfill \\ \end{array} $$

(15)

Nield and Bejan (2006, pp. 308–313) also discuss the paper by CB and the derivation of Eq. (15). The representation

$$ \psi = 2\sum\limits_{k = 1}^N {{b_k}\sin \left( {k\pi z} \right)} $$

(16)

is used to determine the stability criteria $\left( {R_a^*\,,\,\psi } \right)$ with the Galerkin method. With the above representation for Ψ, the requisite boundary conditions, $\psi \; = \;0\; = {\partial ^2}\psi /\partial {z^2}$ are satisfied at z = 0,1. (The ∂ ² Ψ/∂z ² = 0 condition is equivalent to w = 0 by Eq. (8)).

The coefficients, b _k, in Eq. (16) are determined by approximating the differential Eq. (15) using Galerkin′s method. This produces an N × N matrix of coefficients, g _lk , with l as the row number and k as the column number, as follows:

$$ \begin{array}{*{20}{c}} {{g_{lk}} = 2\int\limits_0^1 {{L_{40}}\left[ {\sin \left( {k\pi z} \right)} \right]\sin \left( {l\pi z} \right)dz,\quad k = 1,2, \ldots, N,\quad l = 1,2, \ldots, N} } \\ {\quad = 2\int\limits_0^1 {\left\{ {\begin{array}{*{20}{c}} {\left[ {{{\left( {{k^2}{\pi^2} + {s^2}} \right)}^2} - {s^2}R_a^* \cos \phi } \right]\sin \left( {k\pi z} \right)} \hfill \\ { + i{s_x}R_a^* \sin \phi \left[ { - \left( {z - \frac{1}{2}} \right)\left( {{k^2}{\pi^{2 }}+{s^2}} \right) + k\pi \cos \left( {k\pi z} \right)} \right]} \hfill \\ \end{array} } \right\}\sin \left( {l\pi z} \right)dz} } \\ \end{array} $$

(17)

To evaluate the integrals in Eq. (17), the following identities are needed:

$$ \begin{gathered} \hfill \\ \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \hfill \\ \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \hfill \\ \begin{array}{*{20}{c}} {2\int\limits_0^1 {\sin \left( {k\pi z} \right)\sin \left( {l\pi z} \right)dz = 0,} }{l = k,} \\ { = 1,}{l \ne k;} \\ {2\int\limits_0^1 {\cos \left( {k\pi z} \right)\sin \left( {l\pi z} \right)dz = 0,} }{l = k,} \\ { = \frac{{4l}}{{\left( {{l^2} - {k^2}} \right)\pi }},}{l\pm k\;{\text{odd;}}} \\ {2\int\limits_0^1 {z\sin \left( {k\pi z} \right)\sin \left( {l\pi z} \right)dz = \frac{1}{2},} }{l = k,} \\ { = - \frac{{8lk}}{{{{\left( {{l^2} - {k^2}} \right)}^2}{\pi ^2}}},}{l\pm k\;{\text{odd}}} \\ \end{array} \hfill \\ \end{gathered} $$

(18)

Using these integrals in the expressions for g _lk results in

$$ \begin{array}{*{20}{c}} {{g_{ll}} = {{\left( {{l^2}{\pi^2} + {s^2}} \right)}^2} - {s^2}R_a^* \cos \phi } \hfill \\ {{g_{lk}} = i{s_x}R_a^* \sin \phi \frac{{4kl}}{{{{\left( {{l^2} - {k^2}} \right)}^2}}}\left( {\frac{{2{s^2}}}{{{\pi^2}}} + {l^2} + {k^2}} \right),\quad l\pm k\quad {\text{odd}}} \hfill \\ \end{array} $$

(19)

Let the matrix G _N be given by

$$ {G_N} = \left[ {{g_{lk}}} \right] $$

(20)

Then the instability condition is given by the determinant

$$ \det \left[ {{G_N}} \right] = 0 $$

(21)

For s _x ≠ 0, s _y ≠ 0, solution of this determinant defines $R_a^*$ values for polyhedral cells. Helicoidal cells occur when s _x = 0, s _y ≠ 0. A transitional curve occurs when s _y = 0, s _x = s. In order to calculate this $\left( {R_a^*\,,\,\phi } \right)$curve and simplify the algebra a little, define β and R by

$$ s = \beta \pi, \quad R_a^* = 4{\pi^2}R $$

(22)

and note that the elements of G _N , for N = 6, for example, appear as follows

$$ \begin{array}{*{20}{c}} {{g_{11}}} \hfill & {{g_{12}}} \hfill & 0 \hfill & {{g_{14}}} \hfill & 0 \hfill & {{g_{16}}} \hfill \\ {{g_{21}}} \hfill & {{g_{22}}} \hfill & {{g_{23}}} \hfill & 0 \hfill & {{g_{25}}} \hfill & 0 \hfill \\ 0 \hfill & {{g_{32}}} \hfill & {{g_{33}}} \hfill & {{g_{34}}} \hfill & 0 \hfill & {{g_{36}}} \hfill \\ {{g_{41}}} \hfill & 0 \hfill & {{g_{43}}} \hfill & {{g_{44}}} \hfill & {{g_{45}}} \hfill & 0 \hfill \\ 0 \hfill & {{g_{52}}} \hfill & 0 \hfill & {{g_{54}}} \hfill & {{g_{55}}} \hfill & {{g_{56}}} \hfill \\ {{g_{61}}} \hfill & 0 \hfill & {{g_{63}}} \hfill & 0 \hfill & {{g_{65}}} \hfill & {{g_{66}}} \hfill \\ \end{array} $$

(23)

The first few determinants for fixed N are

$$ \begin{array}{*{20}{c}} {{\text{det}}\,\left[ {{G_{\text{2}}}} \right]\;\; = \;{g_{{\text{11}}}}\,{g_{{\text{22}}}}\; - \;{g_{{\text{21}}}}\,{g_{{\text{12}}}}} \\ {{\text{det}}\,\left[ {{G_{\text{3}}}} \right]\;\; = \;{g_{{\text{33}}}}\;{\text{det}}\,\left[ {{G_{\text{2}}}} \right]\; - \;{g_{{\text{32}}}}\,{g_{{\text{23}}}}\,{g_{{\text{11}}}}} \\ {{\text{det}}\,\left[ {{G_{\text{4}}}} \right]\;\; = \;{g_{{\text{44}}}}\;{\text{det}}\,\left[ {{G_{\text{3}}}} \right]\; - \;{g_{{\text{43}}}}\,\left( {{g_{{\text{3}}4}}\,{\text{det}}\,\left[ {{G_{\text{2}}}} \right]\; + \;{g_{{\text{32}}}}\,{g_{{\text{21}}}}\,{g_{{\text{14}}}}} \right)} \\ {\quad \quad \quad \quad \quad - \;{g_{{\text{41}}}}\;\left[ {{g_{{\text{12}}}}\,{g_{{\text{23}}}}\,{g_{{\text{34}}}}\; + \;{g_{{\text{14}}}}\;\left( {{g_{{\text{22}}}}\,{g_{{\text{33}}}}\; - \;{g_{{\text{32}}}}\,{g_{{\text{23}}}}} \right)} \right]} \\ \end{array} $$

(24)

It is clear that the off-diagonal terms always appear in product pairs of an even row element by an odd row element. This means that i ² = –1 quantities always appear. Moreover, g _kl  = g _lk , such that, if the off-diagonal elements for rows 1,3,5, ..., g _lk are replaced by |g _lk | and for rows 2,3,4, ..., g _lk are replaced by (–|g _lk |) then this development can work with real valued determinants.

The elements of G _N now become

$$ {g_{ll}} = {\pi^4}\left[ {{{\left( {{l^2} + {\beta^2}} \right)}^2} - 4{\beta^2}R\cos \phi } \right] $$

(25)

for the diagonal elements and

$$ {g_{lk}} = {\left( { - 1} \right)^{l + 1}}16{\pi^4}\frac{\beta }{\pi }R\sin \phi \frac{{lk}}{{{{\left( {{l^2} - {k^2}} \right)}^2}}}\left( {{l^2} + k^2 + 2{\beta^2}} \right),\quad l\pm k\quad {\text{odd}} $$

(26)

for the off-diagonal elements.

The common factor π ⁴ may be removed from each row of det[G _N ] = 0. The resulting determinant will produce a polynomial in R of order N whose coefficients are functions of ϕ and β.

R (hence $R_a^*$) may be calculated in the following manner:

For each value of ϕ, set values of N and β, then determine R from det[G _N ] = 0 that gives the lowest magnitude (for some values of N there is more than one solution for R). Then vary β until an even lower minimum value of R is found. Finally, vary N until results are stable at a certain level of precision, e.g. six decimal places.

Determinants were calculated using a standard Gauss-Jordan pivotal method and R was found using the Muller (1956)-Frank (1958) quadratic interpolation method for finding roots (not requiring derivatives). A verification was made using a symbolic algebra package, Maple, for N = 2, 3, 4, 5, by checking the elements of the determinant and the solution for R. The variation of β to find the minimum R was made automatic by also using a quadratic interpolation method.

The main results are given in Table 3. The transition locus for dense values of ϕ, extending the values in Table 3, are shown in Fig. 2. The limiting value of ϕ was found to be ϕ = 31.49033° when β = 0.813. As ϕ increases the required number of terms, N, increases. For values of ϕ <  20°, N = 20 generated the accuracy tabulated. For ${25^o}\; < \;\phi \; \leqslant \;{31.49^o}$, N = 50 was used. For ϕ > 31.49°, N=90 was used. The critical value of ϕ = 31.49033° was arrived at when zeros of det[G _N ] = 0 could no longer be found. A comparison with the results of CB in their Table 1 indicate that the values of their s _L, the same as β, are in good agreement, except for a slight difference at ϕ = 20°, where s _L = 0.965 compared with β = 0.967. The difference might arise from the values of N = 5 and 8 that they used, lower than the 20 used here. In fact β is not very sensitive to changes in N. A comparison with the 4 decimal-place values of their $R_{aL}^* = 4R\cos \phi$ for ϕ = 0 − 30° shows agreement in all their entries except for the minor difference of 6.3680 when ϕ = 30°. Their critical value for ϕ is 31°48′ = 31.8°.

Table 3 Polyhedric-helicoidal transition locus and values used in calculation. Variables are defined in Eq. (22)

Flow stability in a layer of finite extension x = A

A rank 2, Galerkin approximation to a layer of finite extension x = A is

$$ \begin{array}{*{20}{c}} {{C_0} = \left( {1 - z} \right) + {a_{02}}\sin 2\pi z + {a_{11}}\cos \pi x\sin \pi z} \hfill \\ {{U_0} = - R_a^* {\pi^2}{A^2}{b_{11}}\sin \pi x\cos \pi z} \hfill \\ {{W_0} = R_a^* {\pi^2}{b_{11}}\cos \pi x\sin \pi z} \hfill \\ \end{array} $$

(27)

The expressions for C ₀ ,U _0, W ₀ satisfy the boundary conditions and the mass balance Eq. (3). Darcy′s Eq. (4) and the transport Eq. (5) are satisfied approximately. The use of Eqs. (27) in Eqs. (3), (4) and (5) provide expressions for the coefficients:

$$ \begin{array}{*{20}{c}} {{a_{02}} = - \frac{1}{8}R_a^* \pi {a_{11}}{b_{11}}} \\ {{a_{11}} = R_a^* {A^2}{b_{11}}\left( {\frac{{1 + \pi {a_{02}}}}{{1 + {A^2}}}} \right)} \\ {{\pi^2}\left( {1 + {A^2}} \right){b_{11}} = {a_{11}}\cos \phi - \frac{{16}}{{{\pi^3}}}A\left( {1 + \frac{2}{3}\pi {a_{02}}} \right)\sin \phi } \\ \end{array} $$

(28)

Eliminating a ₁₁ and b ₁₁ produces a relationship between ${a_{02}}\;,\;R_a^*$and ϕ:

$$ \frac{{\pi {a_{02}}}}{{1 + \pi {a_{02}}}} = - \frac{1}{{8{\pi^3}}}\left( {1 + \frac{1}{{{A^2}}}} \right)\left[ {\frac{{16AR_a^* \left( {1 + \frac{{2\pi }}{3}{a_{02}}} \right)\sin \phi }}{{R_a^* \left( {1 + \pi {a_{02}}} \right)\cos \phi - {\pi^2}\left[ {{{\left( {1 + {A^2}} \right)}^2}/{A^2}} \right]}}} \right] $$

(29)

The right side of this equation is negative or zero, implying that a ₀₂ is negative or zero. CB incorrectly state that a ₀₂ ≥ 0 (which is, in fact, between 0 and 1/π).

The transition locus between unicellular flow and helicoidal flow is to be found. After development of linear perturbation equations based on the rank 2 approximations and a further Galerkin series approximation, CB produce an additional stability equation involving ${a_{02}}\;,\;R_a^*$ and ϕ independent of the length B:

$$ R_a^* \cos \phi = \frac{{4{\pi^2}}}{{1 + \pi {a_{02}}}} $$

(30)

To find the transition locus relationship between $R_a^*$ and ϕ, an expression for a ₀₂ in terms of only ϕ is first found from the previous two equations as follows. First set

$$ p = 1 + \pi {a_{02}} $$

(31)

so that

$$ R_a^* = \frac{{4{\pi^2}}}{{p\cos \phi }} $$

(32)

After substituting for πa ₀₂ and $R_a^*$ in Eq. (29) it becomes

$$ p\left( {p - 1} \right) + Q{\left( {1 + 2p} \right)^2} = 0 $$

(33)

where

$$ Q = \frac{{512}}{{9{\pi^4}}}\frac{{{A^4}\left( {{A^2} + 1} \right)}}{{{{\left( {{A^2} - 1} \right)}^4}}}{\text{ta}}{{\text{n}}^2}\phi $$

(34)

For the quadratic equation in p, the larger of the two p solutions is expected to produce the smaller $R_a^*$:

$$ p = \frac{{1 - 4Q + \sqrt {{1 - 12Q}} }}{{2\left( {1 + 4Q} \right)}} $$

(35)

With this p, $R_a^*$ is then determined from Eq. (32) and the $\left( {R_a^*\,,\,\phi } \right)$ curves for values of A = {5, 10, 20, 50, ∞} are shown in Fig. 2. Values of φ for these and additional A values are given in Table 4. No real solutions exist for Q < 1/12. At Q = 1/12, p = 1/4 for all A. The corresponding critical angle ϕ _c determined from Eq. (34) for various A values are, for

$$ A = \left\{ {\,{\text{1,}}\,\,{\text{5,}}\,\,{\text{10,}}\,\,{\text{20,}}\,\,{\text{50,}}\,\,{\text{100,}}\,\,\infty } \right\}: $$

$$ {\phi _c}\; = \;\left\{ {{\text{0}}.{\text{0}},\;{\text{59}}.{\text{63}},\;{\text{74}}.{\text{81}},\;{\text{82}}.{\text{41}},\;{\text{86}}.{\text{97}},\,{\text{88}}.{\text{48}},\;{\text{90}}} \right\} $$

and the corresponding $R_a^*$ values from Eq. (32), are

$$ R_a^*\; = \left\{ {\;{\text{157}}.{\text{92}},\;{\text{312}}.{\text{39}},\;{\text{602}}.{\text{79}},\,{\text{1196}}.{\text{04}},\,{\text{2983}}.{\text{73}},\;{\text{5965}}.{\text{66}},\;\infty } \right\}. $$

Table 4 Values of critical Rayleigh number, $R_a^*$, for transition locus between unicellular and helicoidal convection modes for a box of aspect ratio A inclined to the horizontal direction at angle ϕ. Values are plotted in Fig. 2 (with the exception of A = 100). Missing entries correspond to the case Q < (1/12) in Eq. (33) when there are no real solutions

These limits are a result of the rank 2 approximation. A comparison of the curves in Fig. 2 with Fig. 2 of CB indicates that the shapes are similar but the values are not identical.