1 Introduction

Railway ballast generally comprises large, angular particles, typically in the size range 20–50 mm. The main functions of railway ballast are to transmit and distribute the load from the sleepers to the formation, to facilitate maintenance operations to ensure ride quality, and to provide rapid drainage [1]. As granular material, the plastic deformation of ballast caused by the cyclic traffic load results in permanent settlement and thus the deterioration of track geometry [2,3,4]. The reduction of ballast settlement could significantly reduce the maintenance cost for the railway industry. A number of modifications to the conventional ballast system have been proved to be effective in reducing the permanent settlement, such as adding geogrid reinforcement [5,6,7,8], attaching resilient pads (under sleeper pads) to the underneath of sleepers [9,10,11,12], and adding fibre reinforcement to the ballast [13, 14]. This paper aims to explore the possibility of reducing the ballast settlement by simply using layers of ballast with different grading without any additional reinforcement.

Anderson and Key [15] carried out a ‘box test’ using a two-layered ballast system primarily in relation to railway maintenance by stone blowing and found that raising the level of a sleeper by the addition of smaller stones can result in reduced settlements under repeated load. Key [16] designed a group of triaxial tests and box tests on a two-layered sample with various materials of size 14–20 mm on top of standard ballast to investigate how the track maintenance was affected by stone blowing. He found that the weaker layer of material controls the properties of the two-layered triaxial specimen but the (larger) ballast rather than the smaller material controls the deformation in a box test. Claisse et al. [17] and Claisse and Calla [18] explored the possibility of placing finer-sized stones as crib ballast (between the sides of adjacent sleepers) so as to be capable of filling the voids beneath the sleepers, and this system was also named as a ‘two-layered ballast system’. Abadi et al. [19] tested a two-layered ballast using the full-scale Southampton Railway Test Facility: the sample comprised a 250 mm layer of standard grade ballast overlain by a 50 mm layer of 10–20 mm aggregate. The settlement of this two-layered ballast system was found to be less compared with Network Rail standard ballast. Baghosorkhi [20] reported a group of box tests on a two-layered ballast system using 2/3-scaled ballast and full size ballast, and found that the two-layer system behaved better than the sample of single size. However, to the authors’ current knowledge, none of the above work has given a clear explanation as to why two-layered ballast performs better than single-layered ballast.

The discrete element modelling (DEM) introduced by Cundall and Strack [21] has been progressing rapidly for last few decades as it can provide micro mechanic insight for granular materials. DEM has been successfully used to study the mechanical behaviour of railway ballast under various loading conditions such as triaxial tests [22,23,24,25,26,27], box tests [10, 28,29,30,31,32] and direct shear tests [33,34,35,36]. To find out what is occurring at a micro level for the two-layered ballast system and thus potentially propose an optimum design, DEM is employed in this study to simulate the reported experiments [20].

2 Background

This study primarily uses the experimental tests on two-layered ballast reported by Baghosorkhi [20] to compare with new numerical (DEM) results. In these experiments [20], four different samples were tested, with varying combinations of full size ballast and 2/3 scale ballast, in a ‘box test’ previously developed by McDowell et al. [37]. The box test is used to model the ballast-sleeper interaction that occurs under the rail seat of a track, as Fig. 1 shows. The displacement of the sleeper was tracked continuously with four linearly variable differential transformers (LVDTs) mounted at the four corners of the sleeper section, as detailed in [37]. Figure 2 shows the ballast layer arrangements for the four samples tested by Baghosorkhi [20].

  • Test F3: Sample with single 300 mm layer of full size ballast.

  • Test S3: Sample with single 300 mm layer of 2/3 scale size ballast.

  • Test F2S1: A 200 mm layer of full size ballast underneath the sleeper, and a 100 mm layer of 2/3 scale ballast at the base.

  • Test S2F1: A 100 mm layer of 2/3 scale ballast underneath the sleeper, and a 200 mm layer of full size ballast at the base.

Fig. 1
figure 1

Simulated track area of box test

Full size image
Fig. 2
figure 2

Original configurations reported by Baghosorkhi [20]

Full size image

Each test is identified by the type and thickness of ballast used from top to base, for example, test F2S1 corresponds to the sample comprising 200 mm full size ballast on top of 100 mm scaled ballast. It is noted that each test was performed only once for each configuration. The results would be expected to exhibit some (but not significant) scatter, based on the authors’ previous experience.

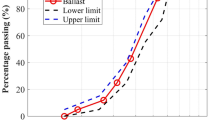
The key results from the experiments are reproduced in Fig. 3 [20]. Test S1F2 has the best performance of all the four samples in terms of permanent settlement. For Test F2S1, higher settlement was observed compared to the sample using only 2/3 scale ballast (Test S3), but less settlement than the full size ballast sample (Test F1). However, comparing tests F2S1 and S1F2, both the ballast interface position and on the relative order of the layers are changed, making it impossible to draw firm conclusions. Given the ability of simulations to extract micro scale information, in this work DEM is used to simulate both the four experimental tests as well as a further two samples [F1S2 and S2F1 (Fig. 4)] to complete the picture and gain a better understanding of the two-layered ballast system.

  • Test F1S2: A 100 mm full size ballast layer underneath the sleeper followed by a 200 mm 2/3 scale ballast layer at the base.

  • Test S2F1: A 200 mm 2/3 scale ballast layer underneath the sleeper followed by a 100 mm full size ballast layer at the base.

Fig. 3
figure 3

Results of settlement of two-layer ballast reported by Baghosorkhi [20]

Full size image
Fig. 4
figure 4

Sample layouts for the additional DEM simulations

Full size image

2.1 DEM simulations

The commercial DEM code PFC3D [38] is used in this study. The box apparatus simulated in DEM is of the same size as used in experiments (0.3 m × 0.7 m × 0.45 m). The dimension of the sleeper section (Figs. 2, 4) is 0.3 m × 0.25 m × 0.15 m and it is loaded vertically with a 3 Hz cyclic load oscillating between 3 and 40 kN (as the experiments). The stress level is achieved using a servo control mechanism. Only 20 cycles are applied for all simulations due to the limit of computational time, whilst also consideringthat the largest settlements always occurred in the first few cycles.

The particles are modelled with a single realistic shape as scanned by Li et al. [39, 40]. For a given scanned particle surface, PFC3D is able to create a ‘clump’ of the same shape by using the algorithm of Taghavi [41]. The detail of generating a clump with irregular shape is given by Li and McDowell [10]. The classic Hertz-Mindlin contact model [38] is used as the contact model and the particles are given a Poisson’s ratio of ν = 0.25 and a shear modulus of G = 28 GPa which are typical values for quartz. The sample is generated by the simple deposition method using the following procedure:

  1. 1.

    The clumps are created in a taller box higher than the box test apparatus and are then allowed to settle under a normal gravity of 10 m/s2.

  2. 2.

    Gravity is increased to 50 m/s2 and then the sample is cycled to an equilibrium state to compact the sample.

  3. 3.

    Gravity is reduced back to 10 m/s2 and then the sample is cycled to equilibrium again. All particles which are not entirely inside the box apparatus or lying inside the boundary of the sleeper are then deleted.

If it is a two-layered sample, the particles lying above the interface layer (100 mm or 200 mm away from the base) were deleted, and then the top layer of the sample was generated following steps 1–3 again.

Figure 5 shows the scanned particle surface, the clump used in the DEM simulations, and an example of the generated sample for test S2F1 (Table 1).

Fig. 5
figure 5

Particle shape used in DEM simulation and sample for test S2F1

Full size image
Table 1 Parameters of clump particle and boundary
Full size table

3 Results and analysis

As the experimental results for the first 20 loading cycles are not available, it is not the aim to compare the DEM simulation results and experimental results quantitatively, but instead qualitatively to understand micro mechanics of two-layered ballast. In each case the simulation was repeated three times (i.e. three different groups of simulated samples). Note that for each group of samples, two single-layered samples (F3 and S3) were first generated with a single random seed and then the two-layered samples were generated by deleting the top layers of these two samples and replacing particles with the other size. In other words, within each single group, configuration F3 (or S3) has exactly the same bottom layer as S2F1 (F2S1) and S1F2 (F1S2). Figure 6 presents the recorded settlements for the six configurations of three groups and the average values after 20 loading cycles, as well as the experimental results [20] after 20,000 cycles. Most of the simulation results for different groups show a scatter of about 5% around the average values except for the configuration F3 in group 1 (10.9% more than the average) and configuration S3 (9.4% less than the average) in group 2. Considering that these angular particles could have rather different particle orientations for each sample within a defined group, the scatter seems acceptable and comparable to what might be expected in the laboratory. There will always be statistical variation for a single configuration (this actually lends credibility to the DEM approach because we can test the same sample again and again, or have different samples and show that the repeatability is similar to laboratory tests). The purpose here is to establish whether there is a general trend, and thus to provide a statistically more economical track bed, accepting that there will be some data that will not follow the general trend; indeed this is normal for lab or field tests. It can be seen that despite the scatter, there is indeed a trend in the observed behaviour for the different configurations.

Fig. 6
figure 6

Settlement for the two-layered ballast in DEM simulation

Full size image

Figure 7 shows the settlement curves for the second group of tests with different configurations. As expected, the results of settlements derived from DEM simulations are following the same pattern (in terms of decreasing settlement) as the four experiments reported by Baghosorkhi [20]. However, the best performance occurred for sample S2F1 for which a 200 mm layer of 2/3 scale ballast is located above a 100 mm layer of full size ballast. For this case, the settlement could be improved by 37% comparing with the test on the full size ballast (Test F3) which is commonly used in industry. It is also noted that within each individual group of samples when the scaled ballast is located underneath the sleeper (sample S2F1, S1F2, S3), the samples settle less than the cases when the full size ballast is located underneath the sleeper (sample F2S1, F1S2, F3). This indicates that reducing the ballast size underneath the sleeper might be helpful for reducing the track settlement. In addition, within each individual group of samples with the same size ballast underneath the sleeper (samples S2F1, S1F2, S3 and samples F2S1, F1S2, F3), the two-layered samples with the interface at 200 mm below the sleeper (sample F2S1 and S2F1) always settle less than the samples with the interface at 100 mm below the sleeper (sample F1S2 and S1F2), and for a given size ballast underneath the sleeper, two-layered systems always perform better.

Fig. 7
figure 7

The settlement curves for the average DEM simulation results for group 2

Full size image

Figure 8 displays the contact force chains of each sample where thickness of each bar is scaled to represent the force magnitude. These are presented in ascending order of settlement: F3 > F1S2 > F2S1 > S3 > S1F2 > S2F1. The top group of samples (F3, F1S2, F2S1) are the samples with full size ballast underneath the sleeper which settle more than the lower group of samples (S3, S1F2, S2F1). It can be seen that the lower group has more uniformly distributed contact forces in terms of both magnitude and orientation. The distribution of contact normal force orientations is shown in Fig. 9 using spherical histograms. The length of each histogram bar is the number of contacts falling within the associated angle. It clearly shows that for the upper group, the contact strong normal force orientations are more concentrated in the vertical direction while for the lower group this is less pronounced. For the purposes of illustration here, only “strong” contact forces (larger than 50 N) were counted. This is because the number of contact forces lower than 50 N takes up nearly 40% of total contact forces and they do not contribute much to the significant force chains.

Fig. 8
figure 8

Contact force chains derived from DEM simulations at max load of 20th cycle

Full size image
Fig. 9
figure 9

Spherical histograms of strong contact normal forces (> 50 N)

Full size image

Figure 10 shows the number of active ballast-sleeper contact normal vectors at the ballast/sleeper interface. Table 2 lists this number for all the conducted simulations for all three groups. It can be seen that for the upper group, fewer contacts are supporting the load from the sleeper and thus each particle underneath the sleeper transmits larger contact forces with fewer contacts. This is consistent with increased particle movement, and can explain why the top group of configurations (full size ballast on top) settles more than the lower group (scaled ballast on top). To verify this assumption, the total displacement vectors of particles under sleeper at the end of the simulation were plotted in Fig. 11. All the six configurations share the same colour bar listed on the left. It is obvious that the particles located under the sleeper have generally smaller displacements for the lower group of configurations.

Fig. 10
figure 10

Contact normal vectors at the sleeper/ballast interface

Full size image
Table 2 Number of contact normal vectors at the sleeper/ballast interface
Full size table
Fig. 11
figure 11

Total particle displacements under the sleeper at the end of 20th cycle

Full size image

Figure 12 illustrates the coordination numbers of various ‘measurement spheres’ in each sample. The measurement spheres are spherical volumes in which the average particle coordination numbers are obtained. In Fig. 12, darker spheres represent higher average coordination numbers. It is clear that for most cases of the two-layered sample (S1F2, S2F1, F1S2, F2S1), the coordination number is higher at the interface between different layers. That is, the particles at the interface on average have more active contacts and then have a greater opportunity for interlocking and reduced horizontal movement, resulting in less settlement compared with the samples of single-layered ballast. To verify this assumption, the average horizontal displacements were simply calculated for all the particles lying across the alternative interface layer locations at 100 mm and 200 mm depth. The values are given for Group1/Group2/Group3 in Fig. 13, which shows that for the configurations with layered ballast, the displacements of particles at the interface layer are less than for the single-layered ballast at the same location. It is noted that the coordination number also varies between horizontally neighbouring measurement spheres. For the 18 samples shown in Fig. 12, the measurement sphere with highest coordination number is always accompanied by stronger contact forces.

Fig. 12
figure 12

Coordination number determined from measurement spheres at max load of 20th cycle for all the conducted simulations of the three groups

Full size image
Fig. 13
figure 13

The average horizontal displacements for all the particles across the interface layer

Full size image

The vertical walls were then each divided into 15 bands to investigate the lateral forces on the wall as shown in Fig. 14. Each band is 30 mm deep which is comparable to the dimensions of a ballast particle. Figure 15 shows an example of the lateral forces acting as a function of depth at the maximum load in the 15th cycle and Table 3 lists all the lateral forces acting on the side boundaries for all the conducted simulations. The vertical axis in Fig. 15 is the distance from the base of the sample. It is found that the two-layered ballast decreases the average lateral force acting on the side boundary especially for the configurations in which the full size ballast is located underneath the sleeper, which is further evidence in addition to the coordination numbers that the two-layered ballast works by reducing particle lateral movement through interlocking of the particles at the interface between different layers. It is proposed that this interlock effect is similar to that provided by geogrid. It also clearly shows that the largest horizontal force always occurs between the third and sixth band from the base, which is 60–180 mm from the base, so the ballast particles within this range are most likely to move laterally. It is expected therefore that enhancing the particle interlock at this region would work most efficiently and this is why the position of the interface at 200 mm (sample F2S1, S2F1) under the sleeper works slightly better than that at 100 mm under the sleeper (sample F1S2, S1F2). Geogrid has long been known to be placed at a similar position to obtain effective performance [8, 28, 42, 43] after the same fashion of tensile reinforcement as a bending beam. Figure 16 plots the same data at the maximum load of the 20th cycle. In this case the maximum lateral loads are all located in the third band which is 60–90 mm from the base. This is again consistent with the typical position of geogrid installed in industry, for example, Tensar [44] reported the geogrid was installed in Shirland in UK at 225 mm underneath the sleeper in 1988.

Fig. 14
figure 14

The side wall divided into 15 layers

Full size image
Fig. 15
figure 15

Lateral forces acting on the side boundary as a function of depth at max load of 15th cycle

Full size image
Table 3 Lateral forces acting on the side boundaries for all the conducted simulations at max load of 15th cycle
Full size table
Fig. 16
figure 16

Lateral forces acting on the side boundary as a function of depth at max load of 20th cycle

Full size image

Following the above discussions, the optimum design for the two-layered ballast system in theory would be sample S2F1. However, as shown by Fig. 6, by enlarging the thickness of the scaled ballast underneath the sleeper from 100 mm (sample S1F2) to 200 mm (sample S2F1), the improvement of settlement is only improved by 4% (from 33 to 37%) whereas the cost and consumption of the scaled ballast is doubled, and scaled ballast is already more expensive than standard ballast. Therefore, sample S1F2 is suggested as the most cost effective design for industry, that is to say, that although the optimum location of the interface appears to be about 100 mm from the base, in terms of cost/economical impact, the scaled ballast being on top is of paramount importance and the position of the interface is secondary; therefore 100 mm scaled ballast over 200 mm full size ballast is the proposed best configuration from those investigated.

4 Conclusions

DEM simulations were performed to replicate previously published experiments on railway ballast, in order to examine previously untried configurations as well as to obtain micro mechanical insight into how two-layered ballast reduces the settlement of ballasted railway track. The DEM simulation results agree with previously reported experiments: the two-layered ballast always settles less than a single-layered ballast. The micro mechanical information extracted from the DEM indicates that the particles at the interface between different layers always have a larger coordination number and thus are more likely to be interlocked and would provide some lateral resistance to movement, much like a geogrid. The analysis also shows that the maximum lateral load acting on the side walls of the box is always about 60–180 mm above the base. This is assumed to be why the two-layered ballast with an interface at 100 mm above the base settles less than that at 200 mm above the base. However, considering the weak improvement by increasing the thickness of scaled ballast from 100 to 200 mm under the sleeper, it is suggested to use a geometry which places 100 mm of scaled ballast on top of 200 mm full size ballast, as the most cost effective layout for the potential application of two-layered ballast in industry. This provides a more homogenous contact force distribution with more contacts under the sleeper, an interface to provide interlock/lateral resistance and minimise the depth of the more expensive scaled (smaller) ballast required to improve performance.