Indices to evaluate the reliability of coarse-grained representations of mixed inter/intramolecular vibrations

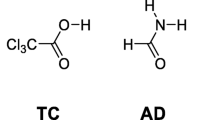
Abstract

We propose some methods for quantifying the reliability of coarse-grained representations of displacement vectors of normal mode vibrations. In the framework of our basic theory, the original displacement vectors are projected onto a lower-dimensional (i.e., a coarse-grained) space. Four types of functions denoted fidelity indices were introduced as measures of the similarity of the original to the restored displacement vectors. These indices were applied to several hydrogen-bonded homodimers, and the behavior of each index was examined. We found that a coarse-grained representation with high reliability resulted in the accurate restoration of properties such as eigenfrequency, modal mass, and modal stiffness.

Appendix: Definition of the coarse-graining matrix

Based on our previous formulation, we can write matrix $\overset{\sim }{\mathbf{B}}$ to transform the atomic displacement vectors of an X-meric molecular assembly from a Cartesian to an internal coordinate system as Eq. A1. Provided that the constituent molecules are nonlinear, matrix $\overset{\sim }{\mathbf{B}}$ is composed of ${\mathbf{B}}_m^{{}^{\circ}},$ representing twelve basic motions, including six translational modes (T_x, T_y, T_z) and six rotational modes (R_x, R_y, R_z). b_m is a set of vibrational motions selected from the first to the (3N_m − 6)th normal mode, where m designates the constituents I, II, ..., X.

$$ \overset{\sim }{\mathbf{B}}=\left(\begin{array}{cccccccc}{\mathbf{B}}_{\mathrm{I}}^{{}^{\circ}}& 0& 0& 0& {\mathbf{b}}_{\mathrm{I}}& 0& 0& 0\\ {}0& {\mathbf{B}}_{\mathrm{I}\mathrm{I}}^{{}^{\circ}}& 0& 0& 0& {\mathbf{b}}_{\mathrm{I}\mathrm{I}}& 0& 0\\ {}0& 0& \ddots & 0& 0& 0& \ddots & 0\\ {}0& 0& 0& {\mathbf{B}}_X^{{}^{\circ}}& 0& 0& 0& {\mathbf{b}}_X\end{array}\right)\kern0.48em $$

(A1)

To construct an appropriate $\overset{\sim }{\mathbf{B}}$ matrix, we need to choose the set of vectors b_m that best represents the intramolecular vibrational motions, as extracted from the results of normal mode analysis for the constituent in its isolated state. However, there is a slight difference between the optimized structure of a constituent in its isolated state and its optimized structure in a molecular assembly. To reduce errors resulting from this discrepancy, we adopted a method to adjust the molecular orientation, namely arranging the principal axes of inertia (a, b, c) of a constituent molecule in its isolated state to coincide with those in the molecular assembly. Under this coordination setting, submatrix ${\mathbf{B}}_m^{{}^{\circ}}$ cannot be uniquely determined, but there is an arbitrariness with respect to the definition of the rotating axes. Even though matrix $\overset{\sim }{\mathbf{B}}$ is not necessarily orthogonal, the MWD vectors (columns in M^1/2$\overset{\sim }{\mathbf{B}}$) will be orthogonal when the rotational axes of a constituent coincide with its principal axes of inertia, and only then will Γ⁻¹ = $\overset{\sim }{\mathbf{B}}$^TM$\overset{\sim }{\mathbf{B}}$ become diagonal. Even when they do not coincide with each other, the definitions of the axes of translation (x, y, z) and rotation (a, b, c) do not influence the reliability of coarse-graining. We should note that the parameters obtained (stiffness and inertial load) are represented based on the given coordinate system and designated as matrix elements like components (T_x, T_x) or (R_a, R_b). Similar attention should be paid when we construct the C matrix. The first six columns of C cannot be uniquely determined, but there is an arbitrariness with respect to the definition of the axes of rotation. The MWD vectors (columns in W = M^1/2C) are orthogonal to each other only when the rotational axes of the molecular assembly coincide with the principal axes of inertia. Although the definitions of the axes of translation and rotation do not affect the result of the coarse-graining calculation, the orthogonality of W influences matrix R and hence the maximum values of the fidelity indices F₁ to F₄.

For example, the matrix for a dimeric molecular system is given by

$$ \overset{\sim }{\mathbf{B}}=\left(\begin{array}{cc}{\mathbf{B}}_{\mathrm{I}}^{{}^{\circ}}& 0\\ {}0& {\mathbf{B}}_{\mathrm{I}\mathrm{I}}^{{}^{\circ}}\end{array}\kern0.72em \begin{array}{cc}{\mathbf{b}}_{\mathrm{I}}& 0\\ {}0& {\mathbf{b}}_{\mathrm{I}\mathrm{I}}\end{array}\right) $$

(A2)

In our previous studies [21,22,23], we used ${\overset{\sim }{\mathbf{B}}}_{Ci}$ specified for a molecular dimer with C_i symmetry. However, this treatment does not greatly affect the result because ${\overset{\sim }{\mathbf{B}}}_{Ci}$ and $\overset{\sim }{\mathbf{B}}$ are connected by the following relation:

$$ {\overset{\sim }{\mathbf{B}}}_{Ci}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{\mathbf{B}}_{\mathrm{I}}^{{}^{\circ}}& {\mathbf{B}}_{\mathrm{I}}^{{}^{\circ}}\\ {}{\mathbf{B}}_{\mathrm{I}\mathrm{I}}^{{}^{\circ}}& -{\mathbf{B}}_{\mathrm{I}\mathrm{I}}^{{}^{\circ}}\end{array}\kern0.6em \begin{array}{cc}{\mathbf{b}}_{\mathrm{I}}& {\mathbf{b}}_{\mathrm{I}}\\ {}{\mathbf{b}}_{\mathrm{I}\mathrm{I}}& -{\mathbf{b}}_{\mathrm{I}\mathrm{I}}\end{array}\right)=\overset{\sim }{\mathbf{B}}{\mathbf{P}}_{Ci} $$

(A3)

using the symmetry-adapted transformation P_Ci composed of the (6 + v) × (6 + v) unit matrix E (v is the number of intramolecular vibrational modes included in the basis set):

$$ {\mathbf{P}}_{Ci}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}\mathbf{E}& \mathbf{E}\\ {}\mathbf{E}& -\mathbf{E}\end{array}\right) $$

(A4)

If we use $\overset{\sim }{\mathbf{B}}$ to obtain the various matrices (stiffness, inertial load, displacement, and mass-weighted displacement), the parameters are designated as matrix elements like (T_x, T_x) and (R_a, R_b) components. Using the P_Ci matrix, we can transform them to the corresponding values for a given coordination system such as the C_i-specific coordination system in which the parameters are designated like (T_x – T_x, T_x – T_x) or (R_a + R_a, R_b – R_b) components:

$$ {\boldsymbol{\Phi}}_{Ci}={{\mathbf{P}}_{Ci}}^{\mathrm{T}}\;\boldsymbol{\Phi}\;{\mathbf{P}}_{Ci} $$

(A5)

$$ {{\boldsymbol{\Gamma}}_{Ci}}^{-1}={{\mathbf{P}}_{Ci}}^{\mathrm{T}}\;{\boldsymbol{\Gamma}}^{-1}\;{\mathbf{P}}_{Ci} $$

(A6)

$$ {\boldsymbol{\Xi}}_{Ci}={{\mathbf{P}}_{Ci}}^{\mathrm{T}}\;\boldsymbol{\Xi} . $$

(A7)

Using an appropriate transformation matrix P, we can also redefine the directions of the x, y, and z axes in order to conveniently clarify the physical meaning of an obtained parameter (e.g., the stiffness of a specific hydrogen bond). In the present study, we defined the xy plane as the least-squares plane of the four atoms participating in the double hydrogen bond and the x-axis as the average of two hydrogen-bonding vectors projected onto the xy plane. Since the obtained parameters of stiffness are represented based on a non-symmetry-adapted coordinate system, those corresponding to translation along the x-axis are designated Φ_Tx,Tx.