WaterScore: a novel method for distinguishing between bound and displaceable water molecules in the crystal structure of the binding site of protein-ligand complexes

Abstract

We have performed a multivariate logistic regression analysis to establish a statistical correlation between the structural properties of water molecules in the binding site of a free protein crystal structure, with the probability of observing the water molecules in the same location in the crystal structure of the ligand-complexed form. The temperature B-factor, the solvent-contact surface area, the total hydrogen bond energy and the number of protein–water contacts were found to discriminate between bound and displaceable water molecules in the best regression functions obtained. These functions may be used to identify those bound water molecules that should be included in structure-based drug design and ligand docking algorithms.

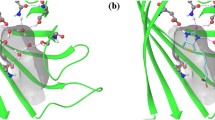
Figure The binding site (thin sticks) of penicillopepsin (3app) with its crystallographically determined water molecules (spheres) and superimposed ligand (in thick sticks, from complexed structure 1ppk). Water molecules sterically displaced by the ligand upon complexation are shown in cyan. Bound water molecules are shown in blue. Displaced water molecules are shown in yellow. Water molecules removed from the analysis due to a lack of hydrogen bonds to the protein are shown in white. WaterScore correctly predicted waters in blue as Probability=1 to remain bound and waters in yellow as Probability<1×10⁻²⁰ to remain bound.

Appendix

We provide a brief outline of multivariate logistic regression analysis. [50, 51, 52] For a binary dependent variable Y that can take values of either 0 or 1, its mean is the proportion of cases of the higher value (1), and the predicted value of the dependent variable (the conditional mean, given the value of the independent variable X and the assumption that Y and X are linearly related) can be interpreted as the predicted probability that an observation falls into such higher value. By definition, the predicted probability lies between 0 and 1. The general shape of the relationship between the probability P(Y=1) and the independent variable X is that of an "S curve", as depicted in Fig. 8.

Fig. 8.

The logistic curve model for the probability P(Y=1) of a binary dependent variable showing a positive correlation with the independent variable X

Instead of predicting the arbitrary value associated with the dependent variable Y, it may be useful to predict the probability that a given observation (as defined by a set of independent variables) will be classified into one of the two values of the dependent variable. Naturally, if we know P(Y=1), we immediately also know the probability of P(Y=0) as P(Y=0)=1−P(Y=1).

If the probability that Y=1 is modeled as P(Y=1)=α+βX, its predicted values may be less than 0 or greater than 1. The first step to avoid this is to replace the probability that Y=1 with the odds that Y=1. The odds that Y=1, written Odds(Y=1), is the ratio of the probability that Y=1 to the probability that Y≠1. Odds(Y=1) is then equal to P(Y=1)/[1−P(Y=1)]. Unlike P(Y=1), the odds has no fixed maximum value, but like the probability, it has a minimum value of 0.

One further transformation of the odds produces a variable that varies, in principle, from negative infinity to positive infinity. The natural logarithm of the odds, ln{P(Y=1)/[1−P(Y=1)]}, is called the logit of Y, and is written logit(Y). This function becomes negative and increasingly large as the odds decrease from 1 to 0, and becomes positive and increasingly large as the odds increase from 1 to infinity. By using the natural logarithm of the odds that Y=1 as the dependent variable, one no longer has the problem that the estimated probability may exceed the maximum or minimum possible values for the probability (see Fig. 8). The equation for the relationship between the dependent variable and a number of independent variables can be then expressed as

$$ {{\rm{logit}}{\left( Y \right)} = \alpha + \beta _{1} X_{1} + \beta _{2} X_{2} + \cdots + \beta _{k} X_{k} } $$

(4)

Calculating back the odds as Odds(Y=1)=exp[logit(Y)] gives us

$$ {{\rm{Odds}}{\left( {Y = 1} \right)} = \exp {\left\{ {{\rm{ln}}{\left[ {{\rm{Odds}}{\left( {Y = 1} \right)}} \right]}} \right\}} = \exp {\left( {\alpha + \beta _{1} X_{1} + \beta _{2} X_{2} + \cdots + \beta _{k} X_{k} } \right)}} $$

(5)

A change of unit in X _i multiplies the odds by exp(β). The odds can be converted back to the probability that Y=1 by the formula P(Y=1)=Odds(Y=1)/[1+Odds(Y=1)], producing the equation

$$ {P{\left( {Y = 1} \right)} = {{\exp {\left( {\alpha + \beta _{1} X_{1} + \beta _{2} X_{2} + \ldots + \beta _{k} X_{k} } \right)}} \over {1 + \exp {\left( {\alpha + \beta _{1} X_{1} + \beta _{2} X_{2} + \ldots + \beta _{k} X_{k} } \right)}}}} $$

(6)

For any given case, logit(Y)=± ∞. This ensures that the probabilities estimated will not be less than 0 or greater than 1. Because the linear form of the model (Eq. 4) can have infinitely large or small values for the dependent variable, ordinary least squares (OLS) cannot be used to estimate the parameters β _i . Instead, maximum likelihood techniques are used to maximize the value of the log likelihood (LL) function, which indicates how likely it is to obtain the observed values of Y, given the values of the independent variables and the parameters α, β₁, ..., β _k . Unlike OLS, which is able to solve directly for the parameters, the solution of the logistic regression model is found by iterating the estimation until the solution converges when the change in the likelihood function is negligible (for the present study, we used a threshold of 1×10⁻⁶, in the routine logitfit.m [53] for Matlab [49]).

Twice the negative of LL has approximately a χ² distribution, which allows one to test the goodness of fit of a model. The value of −2LL for the logistic regression model with only the intercept included is designated D ₀ to indicate that it is the −2 log likelihood statistic with none of the independent variables in the equation. It is analogous to the sum of squares (SST), in linear regression analysis. D _m is analogous to the error sum of squares (SSE) in linear regression analysis, and is sometimes called "deviance", and is twice the negative LL function with the intercept as well as all the independent variables included. D _m is used as an indicator of how poorly the model fits all of the independent variables in the equation. D _m is analogous to the statistical significance of the unexplained variance in a regression model. The most direct analogue in logistic regression analysis to the regression sum of squares (SSR) in linear regression analysis is the difference between D ₀ and D _m:

$$ {G_{{\rm{m}}} = \chi ^{2} = {\left( {D_{0} - D_{{\rm{m}}} } \right)}} $$

(7)

G _m is analogous to the multivariate F-test for linear regression, as well as the regression sum of squares. Treated as a χ² statistic, G _m provides a test of the null hypothesis that β₁=β₂=...=β _k =0 for the logistic regression model. If G _m is statistically significant (with, for example, p<0.05, a 95% confidence level), then the null hypothesis (of random correlation) is rejected and one can conclude that the model allows us to make predictions of P(Y=1).

A natural choice for comparing the strength of the relationship between variables is the analogy to R ² as the sum of the squares of the residuals over the total sum of squares (SST), SST=SSR / SST, in a linear regression model. R _L ² is a proportional reduction in χ² or a proportional reduction in the absolute value of the LL measure.

$$ R_{\rm{L}}^{\rm{2}} = {{G_{\rm{m}} } \mathord{\left/ {\vphantom {{G_{\rm{m}} } {D_0 }}} \right. \kern-\nulldelimiterspace} {D_0 }} $$

(8)

This statistic indicates by how much the inclusion of the independent variables in the model increases the goodness of fit D ₀ to the χ² statistic. R _L ² varies between 0 (for a model in which G _m=0, D _m=D ₀ and the independent variables are useless in predicting the dependent variable) and 1 (for a model in which G _m=−2LL and D _m=0 and the model predicts the dependent variable with perfect accuracy).