Percentile Fragment Size Predictions for Blasted Rock and the Fragmentation–Energy Fan

Abstract

It is shown that blast fragmentation data in the form of sets of percentile fragment sizes, x _P, as function of specific charge (powder factor, q) often form a set of straight lines in a log(x _P) versus log(q) diagram that tend to converge on a common focal point. This is clear for single-hole shots with normal specific charge values in specimens of virgin material, and the phenomenon is called the fragmentation–energy fan. Field data from bench blasting with several holes in single or multiple rows in rock give data that scatter much more, but examples show that the fragmentation data tend to form such fans. The fan behavior implies that the slopes of the straight size versus specific charge lines in log–log space depend only on the percentile level in a given test setup. It is shown that this property can be derived for size distribution functions of the form P[ln(x _max/x)/ln(x _max/x ₅₀)]. An example is the Swebrec function; for it to comply with the fragmentation–energy fan properties, the undulation parameter b must be constant. The existence of the fragmentation–energy fan contradicts two basic assumptions of the Kuz-Ram model: (1) that the Rosin–Rammler function reproduces the sieving data well and (2) that the uniformity index n is a constant, independent of q. This favors formulating the prediction formulas instead in terms of the percentile fragment size x _P for arbitrary P values, parameters that by definition are independent of any size distribution, be it the Rosin–Rammler, Swebrec or other. A generalization of the fan behavior to include non-dimensional fragment sizes and an energy term with explicit size dependence seems possible to make.

1 Introduction

Since the introduction of the Kuz-Ram model for bench blasting (Cunningham 1983, 1987, 2005), much effort has been spent on expressing blast fragmentation in terms of equations for a central measure of the sieving curve, usually the mean x _m = f ₀(q) or median fragment size x ₅₀ = f ₁(q) as functions of specific charge q mainly, plus equations for a parameter like the uniformity coefficient n of the Rosin–Rammler (RR) distribution (Rosin and Rammler 1933). The original Soviet work (Koshelev et al. 1971; Kuznetsov 1973) put up an equation for the mean fragment size x _m that was largely based on the characteristic size x _c obtained from fitting of RR functions to their sieving data and they provided no equation for n.

Cunningham (1983) greatly extended the usefulness of the Soviet formulas for the mean fragment size when he postulated an equation for n = f ₂(geometry) and provided blast engineers with a useful tool for estimating the effect on the whole sieving curve of changing drill pattern, hole diameter, explosive, etc. in their blast designs. The Kuz-Ram model is thus totally dependent on the RR distribution.

It soon became clear that the RR function has two large weaknesses; it usually severely underestimates the amount of fines in a muck pile and it has no largest block size. The fines issue was addressed by researches from the JKMRC in Brisbane when they introduced two bicomponent RR distributions. Firstly, there is the crush zone model (CZM; Kanchibotla et al. 1999), which uses the original RR CDF (cumulative distribution function) for the coarse material and a flatter RR CDF for the fines. Secondly, there is the two-component model (TCM; Djordjevic 1999) which combines two overlapping RR distributions. With this the number of parameters in the prediction formulas increases substantially. For the CZM, e.g., a statically computed crushed zone around the blasthole was said to generate (nearly) all sub −1-mm fines. This fixed one end of the fines CDF. The other end was grafted to the coarse CDF at a point in the percentile size range x ₅₀–x ₉₀, and one pair of parameters (x _c, n) is needed for each branch. Subsequent developments of the CZM have been made (Esen et al. 2003 and Onederra et al. 2004), and this model is widely used in mine to mill applications, see, e.g., Paley (2010).

While percentile sizes like x ₅₀ and x ₈₀ do not rely on the use of an RR or another function to describe the sieving curve, the n values do. So does essentially the mean fragment size x _m since for different distributions it equals different percentile sizes x _P, i.e., the subscript P has become a variable. Even if Cunningham (1983, 1987, 2005) uses the term mean fragment size, his analysis treats the ‘mean’ as if it were the median fragment size. This mistake was brought to light by Spathis (2004, 2009, 2012). In recent papers Ouchterlony (2015a, b) analyzes this and concludes that practical, historical and theoretical arguments do not favor the use of the mean as scale descriptor of a size distribution for blast fragmentation. Thus, the unintended shift from mean to median in the fragmentation prediction equations was actually a positive development.

The coupling of the n-equation to the RR is still a problem though. It has been shown (Ouchterlony 2015b) that force fitting the RR function to sieving data can lead to spurious variations in the fitted n values and erroneous conclusions about how, e.g., drill hole deviations influence the sieving curve or how the use of electronic detonators influences crusher throughput.

The Swebrec function was introduced by Ouchterlony (2005). It is capable of reproducing sieving data really well from the fines range to large boulders, say from 0.5 to 500 mm or three orders of magnitude in fragment size. It has three parameters, x ₅₀, x ₁₀₀ = x _max and b, i.e., two percentile sizes and a curve undulation exponent b. Recent work by Sanchidrián et al. (2014) shows that the Swebrec function is the overall best fitting three-parameter function to sieving data for blasted or crushed rock. Ouchterlony (2005) suggested that the RR function in the Kuz-Ram model be replaced by the Swebrec function to create the KCO (Kuznetsov–Cunningham–Ouchterlony) model. The x ₅₀ prediction equation was retained, and new prediction equations for x _max, the largest stone size, and b were sketched. Even if x ₅₀ and x _max are Swebrec function parameters, they are also valid fragmentation descriptors for any sieving curve. Parameter b though could not at that time be uncoupled from the Swebrec distribution.

The original report on the Swebrec function (Ouchterlony 2003) did not indicate that b would be constant in certain blasting situations but subsequent work on calibrating the KCO model to obtain so-called blast design curves (Ouchterlony et al. 2006, 2010, 2015) indicates that b ought to be independent of specific charge for bench blasting conditions; if not blasting harder would lead to the creation of less fines below a certain size. Other work (Ouchterlony and Paley 2013) provided a way of uncoupling b in the sense that a triplet of percentile sizes, say (x ₅₀, x ₂₀, x ₈₀) could be used to formulate closed form expressions for b and x _max, see also Sect. 3.2. A natural extension of this was that one should focus on determining distribution independent fragmentation prediction equations such as x ₅₀ = f ₁(q), x ₂₀ = f ₃(q) and x ₈₀ = f ₄(q) and let the matter of which distribution function fits the data best be subordinate.

Chung and Katsabanis (2000) took an early step in this direction when they reanalyzed the bench blasting data of Otterness et al. (1991) and produced equations for x ₅₀ = f ₁(q) and x ₈₀ = f ₄(q). They related these expressions to RR type sieving curves through the equation n = 0.842/ln(x ₈₀/x ₅₀). Since the Swebrec function fits the Otterness sieving data much better than the RR does (Ouchterlony 2003), it would be natural to also use the data of Otterness et al. (1991) to generate the equation x ₂₀ = f ₃(q). The base 10 or natural log–log regression fits become with slightly different numbers than given by Ouchterlony (2015b)

$$ \begin{aligned} x_{50} & = \, 47.9/q^{1.22} \;{\text{with}}\;r^{2} = \, 0.88, \, \\ x_{80} & = \, 130/q^{0.82} \;{\text{with}}\;r^{2} = \, 0.80\;{\text{and}}\;\\x_{20} &= 11.6/q^{1.26} \;{\text{with}}\;r^{2} = \, 0.80 \\ \end{aligned} $$

(1a\hbox{-}c)

The fits and the data are shown in Fig. 1. Otterness et al. (1991) were aware that the RR function did not provide satisfactory fits to their data and tried combining RR functions for the fine material and normal distributions for the coarser material with an overlap zone of 38–76 mm and their work focused on quantifying the effects of the drill pattern, spacing, burden and stemming, for example, on the numerical prefactors in Eq. 1a-c.

Fig. 1

Plots of percentile fragment sizes x _P versus specific charge q, derived from sieving data of Otterness et al. (1991)

This paper will, based on the data of Otterness et al. (1991) and much of the data used by Ouchterlony (2003) and some from Sanchidrián et al. (2014), present new findings about distribution-free blast fragmentation formulas, i.e., formulas for percentile fragment sizes x _P = f _P(q). It will start with observations based on blasting of simple geometries in virgin material since it is known that preconditioning of burdens behind blasted rows may change the resulting fragmentation significantly (Johansson and Ouchterlony 2013; Schimek et al. 2013; Katsabanis et al. 2014).

2 Blasting in Materials Without Previous Blast Damage

2.1 Cylindrical Mortar Specimens

The right cylinder with a single through-going hole is perhaps the simplest specimen geometry used in laboratory blasting, and it has been used to investigate the influence of many external factors (Grasedieck 2006; Johansson 2008; Johansson and Ouchterlony 2011). In the first reference, most cylinders were cored from rock samples, and in the latter two references most cylinders were cast of magnetic mortar to increase the reproducibility of the blasting results. Mortar and rock are normally very different materials, yet the sieving curves of the mortar cylinders always follow the Swebrec distribution quite well, see also Ouchterlony (2003), which means that from a fragmentation point of view their behaviors are quite similar; besides, freshly cured mortar cylinders have not been exposed to blast preconditioning.

The 160 some mortar cylinders shot by Johansson (2008) and Johansson and Ouchterlony (2011) were of size D × L ≈ 140 × 280 mm. The mortar was made of 25.6% Portland cement, 31.1% quartz sand, 29.7% magnetite powder, 12.6% water plus plasticizer and defoamer. The measured properties were: density 2510 kg/m³, P-wave velocity 3810 m/s, Young’s modulus 21.9 GPa, Poisson’s ratio 0.22, UCS = 50.7 MPa and Brazilian tensile strength 5.2 MPa.

The data in Table 13 in “Appendix” show the sieving results for a subset that was shot to find the influence of specific charge, q = Q/V where the specimen volume V = πD ²/4 L. The charge size Q was varied by using PETN cord of different strengths: Q/L = 2, 5, 10, 20 and 40 g/m. The specimens were shot in a closed, rubber clad container and the fragments swept up for laboratory sieving in an accredited road laboratory.

Using linear inter- and extrapolation in log(P) versus log(x) space, the percentile size data in Table 14 were calculated. The data for some of these percentile sizes: x ₂₀, x ₃₅, x ₅₀, x ₆₅ and x ₈₀, are plotted in Fig. 2 together with linear regression lines in log–log space.

Fig. 2

Percentile fragment sizes x _P for mortar cylinders versus specific charge q

One notes that the regression lines in Fig. 2 tend to converge to a common, focal point. One way to express this is that the regression lines or rays form a ‘fragmentation–energy fan.’ Regression data for a larger set of fits x _P = A/q ^α are given in Table 14. One notes also that the coefficient of determination is quite high, r ² > 0.97 when P is in the range 10–90%, and that the exponent α is a function of the percentage passing P, α = f ₅(P). α _P or α(P) will be used denote this. The residuals from the curve fits in Fig. 2 are plotted in Fig. 3 together with a fitted normal distribution. The agreement is reasonably good and the data are not very skewed so the linear regression in log–log space has some support.

Fig. 3

Residuals from curve fits in Fig. 2

This tendency for the percentile passing size data to: i) fall on straight lines in log(x _P) versus log(q) space and ii) for these lines to converge to a common point is not a coincidence. A number of examples are given here. First we take the confined mortar cylinders blasted by Johansson (2008) and Johansson and Ouchterlony (2011). The Ø140-mm cylinders were before blasting placed in steel or plastic rings of about Ø300-mm size and the annulus between ring and cylinder packed with aggregate in the size range 0–16 mm. The data are given in Tables 15 and 16 and the results plotted in Fig. 4.

Fig. 4

Percentile fragment sizes x _P for confined mortar cylinders versus specific charge q

A comparison between the data for the free and confined mortar cylinders shows that the data still, but less obviously, tend to fall on straight lines that converge on a different focal point. In the confined case, r ² > 0.97 when P is in the range 20–80%. The whole fan has moved toward larger fragment sizes as expected because of the confinement. The fan has become flatter and narrower, and its focal point has moved toward a lower q value.

Figure 5 shows a comparison of α _P for the two cases, free and confined cylinders together with fits that reproduce α(P). It is clear that α(P) is a monotonically decreasing function of P.

Fig. 5

Exponent α _P or slope of rays in fragmentation–energy fans for free and confined mortar cylinders versus mass passing P

2.2 Less Fines Project Cylinders

Next we consider data from cylinders of rock shot during the Less Fines project (Moser 2005). The sieving data are given by Grasedieck (2006). A series of cylinders of amphibolite and various types of limestone with diameters in the range D = 100–290 mm were shot with a Ø4- or 5-mm hole loaded with PETN powder. The L/ D ratio lay in the range 0.9–2.3 with the ratio being highest for the D = 100-mm specimens. The properties of the rocks are given in Table 1. BIT refers to an amphibolite from Hengl Bitustein AG (⊥ = coring perpendicular to schistosity, //= parallel), CP to a limestone from Cementos Portland SA and NK-‘letter’ to four limestone types from Partek Nordkalk Storugns AB (‘letter’ K = crinoid, S = stromatoporoid, F = fragmentary, R = reef type).

Table 1 Properties of Less Fines rocks according to Grasedieck (2006) Table 2

Table 2 Fragmentation–energy fan data for Less Fines rocks, expressed as $x_{\text{p}} \left( q \right) = A/q ^ {\alpha_{\text{p}}}$

Table 3 x _P-lines data for rock cubes shot by Reichholf (2003)

Table 4 x _P-lines data for cubes and cylinders of Imberg sandstone, D&B means dust and boulders

Table 5 Range of data for all 29 blasts in dolomite quarry tests of Otterness et al. (1991)

Table 6 x _P-lines data for Otterness et al. (1991) all 29 blasts

Table 7 Data for full-scale blasts at Bårarp (Moser et al. 2003, Table 2)

Table 8 Data for full-scale blasts at Vändle (Ouchterlony et al. 2006, Tables 1, 3)

Table 9 Data for full-scale blasts at Långåsen (Ouchterlony et al. 2015, Tables 1, 3)

Table 10 Values of b from regression fits of Swebrec function to sieving data for cylinders of magnetite mortar

Table 11 x _P-lines data for cylinders of Hengl amphibolite

Table 12 Regression line data for x _P, x _P/B and x _P/B ^β data for slab blasting tests of Rustan and Naarttijärvi (1983)

Table 13 Sieving data for blasted mortar cylinders, from Johansson (2008) and Johansson and Ouchterlony (2011)

This time fewer interpolated percentile sizes are presented than for the mortar in Tables 14 and 16. Values for x ₂₀, x ₃₅, x ₅₀, x ₆₅ and x ₈₀ are given in Tables 17, 18, 19, 20, 21 and 22 together with the curve fit parameters A, α and the coefficient of determination r ². Plots of the BIT, CP and NK-F data are shown in Figs. 6, 7 and 8.

Table 14 Calculated percentile sizes x _P, P = 10, 15, 20, … 100, in mm, from data in Table 13

Table 15 Sieving data for confined blasted mortar cylinders, from Johansson (2008) and Johansson and Ouchterlony (2011)

Table 16 Calculated percentile sizes x _P, P = 10, 15, 20,…100, in mm, from data in Table 15

Table 17 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for Hengl cylinders, sieving data in Grasedieck (2006)

Table 18 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for CP cylinders, sieving data in Grasedieck (2006)

Table 19 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for NK-K cylinders, sieving data in Grasedieck (2006)

Table 20 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for NK-S cylinders, sieving data in Grasedieck (2006)

Table 21 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for NK-F cylinders, sieving data in Grasedieck (2006)

Table 22 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for NK-R cylinders, sieving data in Grasedieck (2006)

Fig. 6

Percentile fragment sizes x _P for Hengl amphibolite cylinders versus specific charge q

Fig. 7

Percentile fragment sizes x _P for CP limestone cylinders versus specific charge q

Fig. 8

Percentile fragment sizes x _P for NK-F limestone cylinders versus specific charge q

For the BIT data in Fig. 6, the most highly charged shots, specimens BIT 73A and 73B, marked with symbols × in the figure, were not included in the regression. The x _P values for q ≈ 3 kg/m³ fall considerably below the corresponding extrapolated x _P lines. Since the sieving curves have more of a Rosin–Rammler than a Swebrec character in this case (Moser et al. 2003), one may suspect a different fragmentation process; perhaps surface flaking (spalling) is giving a significant contribution. The x _P lines in Fig. 6 converge on a distant focal point around x ₀ ≈ 1000 mm and q ₀ ≈ 0.025 kg/m³. This point clearly lies outside the range of possible fragmentation outcomes.

For the CP data in Fig. 7, the most lightly charged shot, specimen CP 25, was not included in the regression. The focal point, x ₀ ≈ 900 mm and q ₀ ≈ 0.02 kg/m³, lies close to the focal point in Fig. 6, but the amplitudes A are considerably lower, i.e., the fragmentation is finer. The α _P values for the NK-F data in Fig. 8 and their range 1.01–1.64 are higher than for the BIT and CP data. The focal point lies closer to the fragmentation range, x ₀ ≈ 400 mm and q ₀ ≈ 0.07 kg/m³, but the amplitudes A are roughly the same as for the CP limestone.

The x _P(q) lines of the other three types of NK limestone also show the fragmentation–energy fan behavior. The fan data are summarized in Table 2 as expressed through $x_{\text{p}} \left( q \right) \, = \, A/q ^ {\alpha_{\text{p}}}$.

The coefficient of determination for the x _P lines for the rocks in Table 2 is quite high, for 28 out of 30 values r ² > 0.95. The range for the α _P values is quite narrow for NK-R limestone, 0.94–1.10. This means nearly parallel lines and a focal point far away from the real fragmentation range, x ₀ ≈ 50,000 mm and q ₀ ≈ 0.0003 kg/m³. The widest range of α _P values occurs for NK-F limestone, 1.01–1.64, and the focal point x ₀ ≈ 400 mm and q ₀ ≈ 0.07 kg/m³ lies much closer to, but is still outside the real fragmentation range.

2.3 Cylinders from Quarries with Blasting Tests

Two sets of cylinder tests come from quarries where full-scale blasting tests were also made.

Bårarp quarry, 20 km north of Halmstad in West Sweden (Moser et al. 2003). The rock consists of reddish granitic gneiss with an average grain size of 3–10 mm, a density of 2670 kg/m³, a compressive strength of 225–250 MPa and a tensile strength of 13 MPa. The measured P-wave velocity was 5400–5650 m/s.

Vändle aggregate quarry, 15 km southwest of Västerås in Middle Sweden (Ouchterlony et al. 2006). The rock is a fine- to medium-grained, red to reddish gray granite. Typical data are density 2680 kg/m³, a compressive strength of 206 MPa, a P-wave velocity of 5275 m/s, a brittleness index of 46.8, flatness 1.33 and a grinding index of 2.0–2.6.

The testing procedure for the cylinders was the same as for the Less Fines rocks in Sect. 2.2 using PETN powder in Ø5-mm holes only. The Bårarp data are given in Table 23 and Fig. 9 and the Vändle data in Table 24 and Fig. 10. The most highly charged Bårarp shots, specimens BA 10-2 and 10-1, were not included in the regression. Again the sieving curves for these specimens have more of a Rosin–Rammler than a Swebrec character (Moser et al. 2003; Fig. 5). It is also doubtful whether the most lightly charged Vändle shots, specimens 250-2 and 300-2, should be included in the regression. The data for these specimens seem to fall below the x _P lines defined by the other specimens in Fig. 10. The fragmentation is regular and not of dust and boulders type, however, so these data were included.

Table 23 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for Bårarp cylinders, sieving data in Grasedieck (2006)

Fig. 9

Percentile fragment sizes x _P for Bårarp gneiss cylinders versus specific charge q

Table 24 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for Vändle cylinders, sieving data in Paulitsch (2005)

Fig. 10

Percentile fragment sizes x _P for Vändle granite cylinders versus specific charge q

The Bårarp α _P values and their range 1.00–1.68 are high and nearly identical to those for the NK-F limestone in Table 2. The focal point is not too far away from the fragmentation range, x ₀ ≈ 600 mm and q ₀ ≈ 0,06 kg/m³, and the amplitudes A are roughly the same as for the limestones in Table 2.

The Vändle α _P values and their range 0.98–1.51 are almost as high as those for the NK-F limestone in Table 2 and the Bårarp gneiss in Fig. 8. The focal point is x ₀ ≈ 800 mm and q ₀ ≈ 0.04 kg/m³, and the amplitudes A are roughly the same as for the other rocks except the Hengl amphibolite in Fig. 6. The r ² values of the fits, range 0.88–0.91, are much poorer than for any of the other rocks. One reason for this may be varying rock properties in the quarry or problems to find specimens that were not preconditioned by the previous production blasting. Without the background of the other rock specimens, it is doubtful whether the fan-like character of the set of x _P lines in Fig. 10 would have been considered significant.

2.4 Cubic Specimens

We try to assess here the fragmentation behavior of cubic specimens, as compared with the cylindrical ones in the preceding Sects. 2.1 through 2.3. Reichholf (2003) reports the blasting of approximately cubic blocks with side lengths L = 10, 15, 20, 25, 30 and 40 cm for several different rocks. Most of the blocks, between 5 and 10 per rock type, had a 20 cm side length. These shots were supplemented by one or two blocks of some of the other sizes. A central Ø5-mm drill hole filled with PETN powder constituted the charge. The specific charge for a 20-cm cube was about 0.5–0.6 kg/m³, for the 10-cm ones consequently 4 times higher. For the sieving curves of these tests, Reichholf determined x ₃₀, x ₅₀ and x ₈₀ and also calculated the regression x _P lines x _P(q) = $A/q ^ {\alpha_{\rm p}}$. Table 3 shows the data.

Table 3 shows the same fan-like character of the α _P values, i.e., that they decrease monotonically with increasing P like all the other examples for cylindrical specimens given in Sects. 2.1, 2.2 and 2.3. Their ranges are quite similar too and the computed r ² values just as high.

Reichholf’s (2003) cube data for Imberg sandstone are shown in Fig. 11. The x _P data are given in Table 25. A comparison between the regression fits data in the insert in Fig. 11 with the data in Table 3 shows that the A values are roughly the same but that the α_P values in the figure are much higher. The explanation is that the data for specimens 30_1, 30_2 and 40_1 have been excluded in the fits in Fig. 11 (×symbols) because the sieving curves have a typical dust and boulders (D&B) behavior. Including them in the fits, like Reichholf (2003) in his Fig. 62 did, clearly makes the fitted curves flatter.

Fig. 11

Percentile fragment sizes x _P for Imberg sandstone cubes versus specific charge q

Table 25 Percentile sizes x _P in mm for cubes and cylinders of Imberg sandstone, sieving data in Reichholf (2003) and Grasedieck (2006)

Grasedieck (2006) shot three cylinders of Imberg sandstone with D = 190, 250 and 300 mm, respectively, and q = 0.82, 0.48 and 0.35 kg/m³, respectively. The x _P data for the cylinders are also given in Table 25, and the data for the fits for both cylinders and cubes are compared in Table 4.

Since the cylinder data in Table 4 are based on three shots, two of which gave sieving curves with D&B behavior, a comparison with the cube data that excludes the D&B behavior is impossible. The cylinder data including D&B behavior span over the range q = 0.35–0.82 kg/m³. Reichholf’s (2003) cube data including D&B behavior span over the much wider range q = 0.52–2.5 kg/m³. The α _P values for P = 30, 50 and 80% are almost identical, but this is a coincidence. Fitting x _P lines to cube data over a smaller and comparable range would yield much lower α _P values. The cylinder is in a sense more confined than a cube since the area/volume ratio is smaller and from this and the results for the magnetic mortar in Sect. 2.1 above we would expect the α _P values for the cylinder to be lower. As we seem to have the opposite result that analogy may be false. Thus, we cannot tell how much the shape of the specimen influences the fragmentation–energy fan. What we do know, however, is that for all investigated rocks, the x _P versus q lines tend to form a fan for both specimen types.

2.5 Single Holes in Model Benches (Slabs)

Nie (1988) and Nie and Rustan (1987) did full-scale, single-hole bench blasting with burden B in the range 1.0–4.2 m in the Storugns limestone quarry, belonging to Nordkalk AB. As a comparison model-scale blasting in slabs was made, i.e., in a model bench without a confined bottom. The slabs were of dimensions 300 × 300 × 100 mm thick and one hole was shot in each slab with a burden in the range 5.4–55 mm up to where the breakage stops, i.e., the critical burden B _crit ≈ 55 mm. The Ø6-mm holes were charged with PETN cord, 3 g/m.

The data are also analyzed by Ouchterlony and Moser (2013). With an increasing burden, the sieving data and curve fits show a clear progression from a graded fragmentation to one of dust and boulders. Like in several similar cases, the switch-over burden 30.2 mm is about B _crit/2. Nie (1988; Table 3.2) notes that the specimens with B = 39.7, 42.9 and 45.4 mm have ‘full crater broken in mainly two pieces,’ that specimens with B = 50.1 and 55.0 mm have ‘half crater broken’ and that specimens with B ≥ 42.9 mm have ‘unacceptable fragmentation.’ Thus, in this analysis only specimens with a burden up to B = 34.8 mm were included. Note that an equivalent specific charge that does not include the breakage angle has been used, q′ = Q/$({H}{\cdot}{B} ^2)$ so as to not mix input and result parameters, see comments by Ouchterlony and Moser (2013).

The x _P data and the regression line data are given in Table 26 and Fig. 12. The figure shows that the data contain a relatively large scatter and the convergence of the x _P lines on a common focal point is not very clear. The two specimens with the highest specific charge, those with B = 5.4 and 5.5 mm (q = 103 and 99.2 kg/m³ respectively), were excluded in the fits since their data break the trend of the other data. One expects spalling fracture to start occurring at some level when B decreases but why this should actually give a coarser fragmentation than when B = 10.3 mm (q = 28.3 kg/m³) is not clear. Note that the shots with B = 5.4 and 5.5 mm give nearly the same fragmentation so this observation is probably not an outlier case.

Table 26 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for Storugns slabs, sieving data in Nie (1988)

Table 27 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for dolomite rounds, sieving data in Otterness et al. (1991)

Fig. 12

Percentile fragment sizes x _P for Storugns limestone slabs versus equivalent specific charge q′

The ×-marks to the left are the data for B = 34.8 mm. That sieving curve is a clear case of dust and boulders, so they were also excluded from the fits. Including them would also lower the r ² values for the x _P fits and worsen the tendency of the x _P lines to converge on a common focus.

2.6 One-Tenth Scale Bench Blasting

The data from Otterness et al. (1991) in Fig. 1 refer to 29 bench blasts with 2–4 holes each in massive dolomite with thick horizontal bedding planes, at most 3 planes per meter of bench. Measured P- and S-wave velocities were about 4850 and 2650 m/s, respectively. The benches were prepared with trim blasting and the first hole fired to an obtuse face angle of 110–135°. Extra dynamite tamped to 1120 kg/m³ in plastic tubing was grouted into the drill holes and initiated at the bottom. The delay used was 1 ms/ft or about 3 ms/m of burden. The benches were covered with blasting mats and obvious over- and end-break fragments moved before sieving. The whole round was sieved in-pit down to 9.5 mm.

The test series was conducted to evaluate the parameters that affect the specific charge: burden B, spacing S, bench height H _b, charge diameter d _e and length l _ch, subdrill U _d and stemming l _s. The ranges of the data are given in Table 5.

Otterness et al. (1991) combined Weibull (RR) and normal distribution fits to their sieving data and tried many prediction equations for the percentile sizes x ₂₀, x ₅₀ and x ₈₀. Using the geometrical parameters B, S/B and B/d _e gave the best results. The x _P data and the regression line data from our analysis of their data are given in Table 26 and three x _P lines in Fig. 1. The curve fit parameters are given in Table 6 too.

The data in Table 6 for all 29 blasts are much more irregular than all previous data. At first it was thought that it may have to do with that Otterness et al. (1991) were studying more than the q behavior, i.e., that the wide ranges of other parameters than q in Table 5 might skew the results. Thus, a subset of 10 rounds (#1, 2, 5, 6, 13, 14, 18, 19, 25 and 29) was chosen in which these other parameters varied much less but the x _P line fits for this subset were, however, almost identical to the ones for the full set of 29 blasts so the irregularities in the data probably have a different explanation. The effects of the delay variations are, e.g., not included here but taken into account in the companion work by Sanchidrián and Ouchterlony (2016).

A large range x _P versus q plot for the full set is given in Fig. 13, where the x _P lines are extrapolated toward very low values of q. The x _P lines in the figure do not converge on a common focal point although, except for the x ₂₀ line, the α _P values do form a monotonically decreasing series with increasing P values. The simplest description of the data might be that α _P ≈ 1.25 is constant when P ≤ 0.5 and then decreases with increasing P. One might also hypothesize that there is some upper limit around 0.3 m imposed by the jointing and that this causes the x ₆₅ and x ₈₀ lines to become flatter or to be nonlinear as they approach this limit.

Fig. 13

Percentile fragment sizes x _P for 29 dolomite benches versus specific charge q. Data from Otterness et al. (1991)

2.7 Full-Scale Bench Blasting

Three examples of fragmentation in large-scale, production blasts are presented in this section, all three carried out in Swedish quarries: Bårarp, Vändle and Långåsen.

The Bårarp full-scale blasts were primarily made to investigate how fines from blasting are produced and how their amount can be reduced, see Moser et al. (2003) and references therein. Seven single-row rounds were blasted in a 5-m-high bench during 2000–2002, with different hole dimensions but with a roughly constant specific charge in all the blasts. The theoretical tonnage varied from around 240 tonne up to 420 tonne. Burden, spacing and the number of holes per blast were adjusted to the constant specific charge. Before every new blast smooth blasting of the bench was performed with detonating cord in order to reduce the remaining damage zone from previous blasting. Structural mapping and core drilling were also made. The rock is briefly described in Sect. 2.3.

After each blast, the rock was screened in three steps: (1) a Hercules rotary drum sizer sieved the muck pile to five fractions (−200, 200–350, 350–400, 400–500 and +500 mm and boulders were weighed), (2) an Extec sizer sieved the −200-mm material to four sub-fractions (−25, 25–90, 90–120 and +120 mm) and (3) the −25-mm fraction was quartered and sieved, creating a total of 19 fractions ranging from −0.075 mm to +500 mm.

Basic data from the blasts are given in Table 7. All the blasts except for blast 2 had fully charged holes. All the holes were stemmed with 4- to 8-mm gravel.

All blasts were charged with cartridged emulsion Emulite 100 (blasts 1–3) or its successor Kemix (blasts 4–7) from Dyno Nobel with explosive energies of 2.7 and 3.2 MJ/kg, respectively. Round 2 was blasted with decoupled charges: coupling factor 51/76 ≈ 0.67. JWL isentropes for the emulsions derived from cylinder tests were used to estimate the internal energy depletion along the expansion (Sanchidrián et al. 2015). At the relative volume (1/0.67)² ≈ 2.22, the energy of the detonation products is 0.47 of the energy for an explosive in a fully charged hole. So the specific explosive energy used for round #2 was not 2.7 MJ/kg but 1.269 MJ/kg, and the specific charge in Em 100 equivalents was 0.57·0.47 ≈ 0.27 kg/m³.

The sieving data are given, for example, by Olsson et al. (2003). The Swebrec function does an excellent job of reproducing the sieving curves (Ouchterlony 2003, Table 1). The x _P-data and the regression line data are given in Table 28 and plotted in Fig. 14. These data contain more scatter than the 1/10 scale bench data in Fig. 13, r ² now lies in the range 0.42–0.66 instead of 0.75 and above. This is not unexpected because of testing under field conditions with a narrow range of q values.

Table 28 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for Bårarp rounds, sieving data in Olsson et al. (2003)

Fig. 14

Percentile fragment sizes x _P for Bårarp benches versus specific charge q _Em100 in Emulite equivalent (Olsson et al. 2003)

Four of the five x _P(q _Em100) lines trend toward a relatively well-defined focal point but x ₃₅(q _Em100) does not. Figure 14 shows that the trend lines are largely governed by the data set for q _Em100 = 0.27 kg/m³, i.e., by the one round #2 with decoupled charges. In so far the results in Fig. 14 are only a relatively weak support of the existence of a fragmentation–energy fan but neither are they an argument against.

The larger scatter in the data from full-scale blasts as compared to model-scale blasts is quite natural and may have many reasons. Firstly, as only parts of the muck piles are sieved, there is a sampling error involved. Secondly, the blasted volume has rock and rock mass properties that vary much more. Thirdly, the blasting geometry is often far from ideal; there are drill hole deviations, the drill hole diameter is not constant due to bit wear, the charge densities and lengths may vary, and as high-speed films show the stemming retention varies greatly between holes, etc.

The second case of full-scale bench blasting data comes from the testing in the Vändle quarry (Ouchterlony et al. 2006). The work was done in order to predict the effect of the specific charge on fragmentation and to assess the contribution of blasting and primary crushing to the −32-mm fines. Two 25,000-tonne blasts divided into halves were monitored. Each half had an expanded or a shrunken pattern in order to lower or raise the specific charge. A normal round used Ø90-mm drill holes, angled 10° on a 3 × 4 m pattern with Titan 6080 or 6075, a gassed bulk emulsion blend with 20 or 25% of AN prills. The test rounds lay directly behind each other, with a shrunken pattern behind an expanded one and vice versa to minimize the influence of geology. From the muck piles, four test piles of about 500 tonne were extracted. About a quarter of each was sieved in four steps and fines samples taken. The material was replaced and the whole pile fed to through the primary crusher while measuring the effect and the fines produced. The rock properties are briefly described in Sect. 2.3. The fragmentation size distribution of the muck piles was constructed using the on-site sieving data and the sieved laboratory samples.

Basic data from the blasts are given in Table 8. L stands for lower specific charge than normal and H for higher. All four rounds had four rows of holes and the average bench height lay in the range 11–13 m. Nonel Unidet V-type initiation was used with 42-ms in-row delay and 42-ms (row 1–2) or 67-ms (rows 2–3 and 3–4) between-rows delay.

The original sieving data are given in Ouchterlony et al. (2006). The Swebrec function does an excellent job of reproducing the sieving curves, see Table 9 in Ouchterlony et al. (2006). The x _P-data and the regression line data are given in Table 29 and the relevant parts plotted in Fig. 15.

Table 29 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for Vändle rounds, sieving data in Ouchterlony (2005)

Fig. 15

Percentile fragment sizes x _P for Vändle benches versus specific charge q, data from Ouchterlony et al. (2005)

The series of α _P values decreases monotonically with increasing P so the x _P lines in Fig. 15 tend to converge but if there is a common focal point it is far from well defined, as is the case in Fig. 14. Thus, the results in Fig. 15 are also only a relatively weak support of the existence of a fragmentation–energy fan but neither are they an argument against.

The final example given is the relatively recent fragmentation data from the Långåsen quarry of NCC Roads AB near Arlanda airport (Ouchterlony et al. 2010, 2015) where, among other studies, the use of electronic detonators in quarry blasting was evaluated.

The rock mass is dominated by a gray, fine- to medium-grained granodiorite (1–3 mm) with characteristic amphibole crystals (1–2 mm). It contains 30–40% quartz, about 50% feldspars and biotite, etc. There are few microcracks, the grain boundaries are strong, and the degrees of metamorphism and weathering in the test area are low. The rock data are roughly a density of 2677 kg/m³, a uniaxial compressive strength of 206 MPa and a P-wave velocity of 5275 m/s. Coarse crystalline (2–4 cm) pegmatite dikes occur relatively frequently. They may be 0.5–1 m wide or more and sometimes 10 m long. The jointing in the quarry is dominated by a steeply dipping set striking N20–70°E, which made this set nearly perpendicular to the bench face of the four main testing rounds.

These four rounds each had about 100, Ø89-mm holes in a 14- to 19-m-high bench charged with Titan 6075 or 6080 SME emulsion explosive. The round size was about 12–14,000 m³. In rounds 1 and 2, a tighter pattern than normal was used in one half of the rounds, raising the specific charge there from q ≈ 0.7 to 1.0 kg/m³. Round 1 was thus divided into parts 1-N (normal q) and 1-H (high q) fired in the same blast and round 2 similarly divided into 2-N (behind 1-H) and 2-H (behind 1-N). Nonel initiation was used with two holes per 25-ms delay in-row and 67-ms between rows. Rounds 3 and 4 used electronic delay detonators and different delay times. They gave unexpected results and are not incorporated here, but they are included in the analysis of Sanchidrián and Ouchterlony (2016) where the more complicated effects of joint spacing and delay time are considered. Data for the blasts are given in Table 9.

Eleven 400-tonne samples were taken from the muck piles and sorted in the quarry. Smaller samples were sieved in the laboratory. The laboratory data made up a 0- to 45-mm fines tail that was grafted onto the in-pit sorting data to form sieving curves for the test piles. These curves were then compensated for the use of a grizzly and the absence of boulders to construct the sieving curves for the whole blasted muck pile (Ouchterlony et al. 2010, 2015). The grafting procedure of the fines tail to the in-pit sorting data was made with log–log interpolation, which changes the previous values marginally. The percentile size values x ₂₀ to x ₈₀ and the x _P line regression fits are given in Table 30 and shown in Fig. 16.

Table 30 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for Långåsen rounds, data in Ouchterlony et al. (2010)

Fig. 16

Percentile fragment sizes x _P for Långåsen benches versus specific charge q, data from Ouchterlony et al. (2010)

The series of α _P values do not decrease monotonically with increasing P, so the x _P lines in Fig. 16 do not converge. The results look somewhat like those for the Otterness et al. (1991) test in dolomite benches in Figs. 1 and 13, i.e., one where the simplest interpretation is that α _P is constant in the range P ≤ 65% and then smaller when P = 80%. This would mean parallel x _P lines with a focal point at infinity. The number of data is so low, however, that a definite conclusion about this matter cannot be drawn.

Sanchidrián and Ouchterlony (2016) have collected sieving data from 169 bench blasts in different sites and rock types, different bench geometries and different delay times, for which the design data for the blasts and the size distributions of the muck piles obtained by sieving were available. These blasts include the 29 blasts by Otterness et al. (1991) described in Sect. 2.6 plus the seven Bårarp rounds, the four Vändle half-rounds and the four Långåsen half-rounds described in this section. The data are plotted in Fig. 17 together with the best fit lines x _P = f(q·e).

Fig. 17

Percentile fragment sizes x _P for 169 bench blasts versus qe, Sanchidrián and Ouchterlony (2016) Fig. 13

Here, e (MJ/kg) is the heat of explosion of the explosive so that q·e is an energy concentration, or energy powder factor; the use of it instead of the plain (mass) powder factor gives a common basis of comparison for all 169 rounds, in which different explosives were used.

The data in Fig. 17 scatter enormously because of the wide span in blasting conditions, of which probably the most significant is the scale of the blast (e.g., the burden, which spans more than one order of magnitude). Even so the average behavior of the fragmentation data with specific charge is a convergence of the x _P fan lines, which is not as clear in some of the individual cases presented in Sects. 2.6 and 2.7. We may take this average behavior as a further indication that in general the x _P lines for bench blasting rounds tend to meet at a common focal point in log(x _P) versus log(qe) space, or that in some cases, such as Långåsen, they may be parallel. These data are not final evidence but taken together with the data from the single-hole blasts in cylinders, cubes and slabs they allow us to formulate a hypothesis.

3 The Fragmentation–Energy Fan

3.1 Hypothesis and Consequences for Fragment Size Distribution

The material in Sect. 2 makes it possible to state the following hypothesis: When blasting in a given geometry and changing the specific charge, either through changing the charge size (hole diameter) or through a change in geometry through the breakage burden, for example, then the fragmentation can be described by percentile mass passing x _P versus specific charge relationships of power-law type that for different P-values converge to a common focal point (x ₀, q ₀ ).

This power-law relationship is valid within a limited range of q values. Blasting too hard, i.e., with too high q values, gives a different fragmentation. Not blasting hard enough gives a dust and boulders fragmentation where the coarse end of the sieving curve is characterized by a few discrete, large blocks and at some limit q value no fragmentation at all. The largest conceivable block size is the specimen split in halves or the breakage region broken out in one piece, with small amounts of dust created by the crack propagation that defines the breakage (Ouchterlony and Moser 2013). The focal point usually lies outside this region in x versus q space and may, practically seen, lie at infinity. For blast damaged and jointed material, this convergence of the x _P lines on a common focal point is subject to substantial scatter in the individual cases but not so as an average overall behavior, see Fig. 17.

The power-law relationships become the fragmentation–energy fan rays in log(x _P) versus log(q) space. They may be written for arbitrary values of P

$$ x_{\text{p}} /x_{0} = \left( {q_{0} /q} \right)^{\alpha (p)} \,{\text{or}}\,\alpha \left( p \right)= \ln \left( {x_{\text{p}} /x_{0} } \right)/\ln \left( {q_{0} /q} \right) = \ln \left( {x_{0} /x_{\text{p}} } \right)/\ln \left( {q/q_{0} } \right) $$

(2)

The focal point (x ₀, q ₀) depends, probably, on blast geometry and the material blasted. α(P) is a monotonically decreasing function of P and may for given blast conditions be inverted to give

$$ P = \alpha^{ - 1} \left( P \right) = F_{0} \left[ {\ln \left( {x_{0} } \right/x)/\ln \left( {q/q_{0} } \right)} \right] \, = F_{0} \left[ {{\text{Arg}}_{0} } \right] \, = P\left( {x, \, q} \right)\,{\text{for}}\,x < x_{0} \,{\text{and}}\,q > q_{0} $$

(3)

where the general notation x is used for the sieve size, instead of x _P, as the actual P value for a pair of (x, q) data is now determined by the function P itself. Since P must grow with increasing x and Arg₀ decreases with increasing x, F ₀ denotes a suitable monotonically decreasing function of the argument Arg₀. For all x on one of the lines defined by Eq. 2, Arg₀ = constant and hence P = constant.

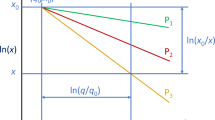
A geometric interpretation follows immediately from the proportions of side lengths in similar triangles with a common vertex at (x ₀, q ₀) since ln(x ₀/x) = ln(x ₀) − ln(x) and ln(q/q ₀) = ln(q) − ln(q ₀), see Fig. 18.

Fig. 18

Fragmentation–energy fan with similar triangles, case Arg₀

Choose two specific percentile size values, the median and maximum fragment sizes x ₅₀ and x ₁₀₀ = x _max. From Eq. 2 it follows that

$$ \ln \left( {x_{0} /x} \right) \, = \, \ln \left( {x_{0} /x_{\hbox{max} } } \right) \, + \, \ln \left( {x_{\hbox{max} } /x} \right) \, = \alpha_{100} \cdot\ln \left( {q/q_{0} } \right) \, + \, \ln \left( {x_{\hbox{max} } /x} \right) $$

(4a)

$$ \ln \left( {x_{\hbox{max} } /x_{50} } \right) \, = \, \ln \left( {x_{\hbox{max} } /x_{0} } \right) - \ln \left( {x_{50} /x_{0} } \right) \, = \, \left( {\alpha_{50} {-}\alpha_{100} } \right)\cdot\ln \left( {q/q_{0} } \right) $$

(4b)

Then it also follows that

$$ \ln \left( {x_{0} /x} \right)/\ln \left( {q/q_{0} } \right) \, = \alpha_{100} + \, \left( {\alpha_{50} - \alpha_{100} } \right)\cdot\left\{ {\ln \left[ {x_{\hbox{max} } \left( q \right)/x} \right]/\ln \left[ {x_{\hbox{max} } \left( q \right)/x_{50} \left( q \right)} \right]} \right\} $$

(5a)

Eq. 5a represents a linear transformation of the argument Arg₀ in Eq. 3:

$$ {\text{Arg}}_{0} = \alpha_{100} + \, (\alpha_{50} - \alpha_{100} )\cdot{\text{Arg}}_{1} $$

(5b)

Arg₁ being the logarithm ratio in curly brackets in Eq. 5a. Substituting Arg₀ in Eq. 3 yields

$$ P = F_{0} \left[ {{\text{Arg}}_{0} } \right] \, = F_{0} [\alpha_{100} + \, (\alpha_{50} - \alpha_{100} )\cdot{\text{Arg}}_{1} \left] { \, = F_{1} } \right[{\text{Arg}}_{1} ] $$

(6a)

which, since α ₅₀ − α ₁₀₀ > 0, turns out to be also a monotonically decreasing function of Arg₁. We may write, finally:

$$ P\left( {x,q} \right) \, = F_{1} \left[ {\ln \left( {x_{\hbox{max} } /x} \right)/\ln \left( {x_{\hbox{max} } /x_{50} } \right)} \right] $$

(6b)

where the dependence on q is borne only in the values of x ₅₀ and x _max. This makes this form of P(x, q) useful for describing the sieving curve of a specific test, i.e., to describe P(x, q = const.), see Fig. 19.

Fig. 19

Fragmentation–energy fan with similar triangles, case Arg₁

Similarly, if F ₁[ln(x _max/x)/ln(x _max/x ₅₀)] is determined by curve fitting to fragmentation data that show fragmentation–energy fan behavior with the focal point (x ₀, q ₀), then, from Eq. 5b and the expression for Arg₀ in Eq. 3, there follows that

$$ P\left( {x,q} \right) \, = F_{1} \left\{ {\left[ {\ln \left( {x_{0} /x} \right)/\ln \left( {q/q_{0} } \right){-}\alpha_{100} } \right]/\left( {\alpha_{50} {-}\alpha_{100} } \right)} \right\} $$

(7)

Note that it is possible to choose other percentile sizes than x ₅₀ and x _max, e.g., x ₂₀ and x ₈₀, and to derive specific function forms of F ₀ and F ₁ adapted to them.

The properties of the fragmentation–energy fan and hence of P(x,q) are such that when x increases then the value P(x,q = const.) must increase monotonically because when the sieve size increases, the mass passing must increase. At the same time, P(x = const., q) must increase monotonically with increasing q because when one blasts harder in the same geometry, more fine material of a given size must be produced. The latter argument means that even if there were no common focal point for the percentile size lines x _P(q), these lines cannot cross in the q range where they are valid.

3.2 Relationships for Swebrec Function

Arg₁ of F ₁ in Eqs. 6a, 6b is recognizable as the argument of the basic Swebrec function (Ouchterlony 2003, 2005). The basic Swebrec function is consistent with the fragmentation–energy fan behavior of blasting provided that b is independent of q, see below. Since they do not contain logarithm ratios in the argument, the RR and transformed versions thereof are not consistent with this fragmentation behavior. In Ouchterlony (2015a, b), it was pointed out that the RR function is consistent with the special case that α(P) = constant, i.e., with parallel percentile size lines x _P at spacings given by n that have no focal point or alternatively expressed, consistent with lines that have a focal point at infinity. The CDF of the basic Swebrec distribution reads (Ouchterlony 2005, 2009a)

$$ P\left( x \right) \, = \, 1/\left\{ {1 \, + \, \left[ {\ln \left( {x_{\hbox{max} } /x} \right)/\ln \left( {x_{\hbox{max} } /x_{50} } \right)} \right]^{b} } \right\}\quad {\text{when}}\quad x < x_{\hbox{max} } $$

(8)

Recent work (Ouchterlony and Paley 2013) showed that b and x _max could be expressed as closed form expressions of three size percentiles like x ₅₀, x ₂₀ and x ₈₀ through the equations.

$$ b = \, \ln \left( 4 \right)/\ln \left[ {\ln \left( {x_{50} /x_{20} } \right)/\ln \left( {x_{80} /x_{50} } \right)} \right] $$

(9a)

$$ 1/\ln \left( {x_{\hbox{max} } /x_{50} } \right) \, = \, 1/\ln \left( {x_{80} /x_{50} } \right){-}1/\ln \left( {x_{50} /x_{20} } \right) $$

(9b)

Again the logarithm ratios have a geometrical interpretation, see Fig. 20.

Fig. 20

Fragmentation–energy fan with similar triangles for Swebrec function

With small changes, Eqs. 9a, 9b are also valid for x ₅₀ and any percentile size pair x _P1 and x _P2 for which P ₁ + P ₂ = 1 or 100%, e.g., x ₂₅ and x ₇₅. In the latter case, the 4 in Eq. 9a is replaced by 3 or in the general case by the term P ₁/P ₂ where P ₂ < 0.5. As x _max > x ₅₀ it follows from the generalized Eq. 9b that x ₅₀/x _P2 > x _P1/x ₅₀ and then from Eq. 9a that b > 0.

From Eq. 9a it follows that when the logarithm ratio is constant, i.e., when b is independent of q, the Swebrec function describes a fragmentation–energy fan. Alternatively from Eq. 6b, for the q dependence to stay confined within the logarithm ratio, b must be independent of q. The idealized behavior that this implies is by no means apparent from the original Swebrec function fits to the sieving data, even if the coefficient of determination of the fitted curves is very close to 1. Table 10 and Fig. 21 show the best fit values of b for the Johansson (2008) and Johansson and Ouchterlony (2011) specimens (see the fragmentation data in Tables 13 and 14).

Fig. 21

Swebrec function undulation exponent b versus specific charge

The linear regression b(q) for the free cylinders has a slope that is not significantly different from zero and all b values for the confined cylinders fall within the confidence limits. Thus, b = 2.33 ± 0.45, constant and independent of q is an acceptable summary of the b data, but the coefficient of variation (COV) is quite large. At the time when these tests were made there was no hypothesis stated and little direct evidence to suggest that b(q) = constant.

Considering that the fitting process with the Swebrec function creates a certain smoothing of the data, a COV of nearly 20% is quite high. Using the interpolated x ₂₀, x ₅₀ and x ₈₀ data in Tables 14 and 16 and Eq. 9a to calculate b involves no such smoothing and would almost double the COV.

Inserting the Swebrec function into Eqs. 2 and 5a, we obtain

$$ \alpha \left( P \right) \, = \alpha_{100} + \, \left( {\alpha_{50} - \alpha_{100} } \right)\cdot\left[ {1/P - 1} \right]^{1/b} $$

(10)

Using the data for the x ₅₀ and x ₁₀₀ lines in Tables 14 and 16 to get the exponents α ₁₀₀ and α ₅₀ for the free and confined mortar cylinders and setting b = 2.33 for both free and confined cylinders, we can compute α(P), see Fig. 22 where the α ₁₀₀ values have been manipulated a bit to improve the fits: 0.25 instead of 0.383 for the free cylinders and 0.10 instead of 0.072 for the confined ones.

Fig. 22

Slope of rays in energy fans for free and confined mortar cylinders versus mass passing P with Swebrec curve fits

The agreement in Fig. 22 between the data and the expression for α(P) in Eq. 10 is encouraging, considering that the b values of the fitted Swebrec functions in Table 10 vary a lot, see also Fig. 5.

Another question to be asked is what happens if b(q) is allowed to vary. We assume that the fragmentation will always be finer when we blast harder, i.e., that

$$ \Delta P(x,q) > 0\,{\text{for}}\,{\text{all}}\,x\,{\text{when }}\Delta q > 0 $$

(11)

For conciseness, write the basic Swebrec function with Arg₁ = R as

$$ P\left( {x;x_{50} ,x_{\hbox{max} } ,b} \right) \, = \, 1/\left[ {1 \, + R^{b} } \right]\quad {\text{where}}\quad R = R\left( {x;x_{50} ,x_{\hbox{max} } } \right) $$

(12)

Then the inequality (11) becomes, using the chain rule for partial derivatives

$$ \Delta P = \frac{\partial P}{\partial q} \cdot \Delta q =\left( {\frac{\partial P}{{\partial x_{50} }} \cdot \frac{{\partial x_{50} }}{\partial q} + \frac{\partial P}{{\partial x_{\hbox{max} } }} \cdot \frac{{\partial x_{\hbox{max} } }}{\partial q} + \frac{\partial P}{\partial b} \cdot \frac{\partial b}{\partial q}} \right) \cdot \Delta q > 0 $$

(13)

Use of Eq. 12 to calculate the partial derivatives yields

$$ \frac{\partial P}{{\partial x_{50} }} = \frac{-1}{{[1 + R^{b} ]^{2} }} \cdot \frac{{\partial (R^{b} )}}{{\partial x_{50} }} $$

(14)

and similar expressions for the derivatives with respect to x _max and b. The partial derivatives of R ^b are, from Eq. 12 and further manipulation:

$$ \frac{{\partial (R^{b} )}}{{\partial x_{50} }} = \frac{{bR^{b} }}{{x_{50} \cdot \ln (x_{\hbox{max} } /x_{50} )}} $$

(15a)

$$ \frac{{\partial (R^{b} )}}{{\partial x_{\hbox{max} } }} = \frac{{bR^{b} }}{{x_{\hbox{max} } \cdot \ln (x_{\hbox{max} } /x_{50} )}} \cdot [1/R - 1] $$

(15b)

$$ \frac{{\partial (R^{b} )}}{\partial b} = \ln (R) \cdot R^{b} $$

(15c)

The derivatives of x ₅₀ and x _max with respect to q are calculated from the fan lines, Eq. 2:

$$ \frac{{\partial x_{50} }}{\partial q} = - \alpha_{50} \cdot x_{50} /q $$

(16a)

$$ \frac{{\partial x_{100} }}{\partial q} = - \alpha_{100} \cdot x_{\hbox{max} } /q $$

(16b)

and with insertion of Eqs. 14, 15a, 15b, 15c, 16a, 16b into Eq. 13, there results

$$ \Delta P = \frac{{bR^{b} }}{{\left[ {1 + R^{b} } \right]^{2} }} \cdot \left\{ {\frac{{\alpha_{50} }}{{\ln \left( {x_{\hbox{max} } /x_{50} } \right)}} + \frac{{\alpha_{100} }}{{\ln \left( {x_{\hbox{max} } /x_{50} } \right)}} \cdot \left[ {1/R - 1} \right] - \frac{q}{b} \cdot \frac{\partial b}{\partial q} \cdot \ln \left( R \right)} \right\} \cdot \frac{\Delta q}{q} $$

(17)

When x = x ₅₀, then R(x) = 1 and the second and third terms inside the curly brackets vanish. Since α ₅₀ > 0 the condition ΔP > 0 when Δq > 0 is met when x = x ₅₀. When x > x ₅₀, then R(x) < 1, 1/R − 1 > 0 and ln(R) < 0. When x → x ₅₀ from above then [1/R − 1]/ln(R) → −1, but when x → x _max then the factor 1/R dominates over ln(R). Thus, as α ₁₀₀ ≥ 0 (since we do not expect a larger maximum size when we blast harder) the sum of the three terms within curly brackets becomes positive for all x ₅₀ < x < x _max, if the following condition is fulfilled:

$$ \frac{q}{b} \cdot \frac{\partial b}{\partial q} \ge 0 $$

(18a)

When x < x₅₀, then R(x) > 1, 1/R − 1 < 0 and ln(R) > 0. When x → 0, then R → ∞ and 1/R − 1 → −1 stays finite and the first term within the curly brackets dominates over the second one since α ₅₀ ≥ α ₁₀₀. However, since ln(R) → ∞ the third term will dominate over the first two. To keep ΔP > 0 requires that

$$ \frac{q}{b} \cdot \frac{\partial b}{\partial q} \le 0 $$

(18b)

Inequalities 18a and 18b are only satisfied if ∂b/∂q = 0, i.e., if b(q) = constant. This result was anticipated in the judgment made with the KCO model design curves for blasting in the Vändle and Långåsen quarries (Ouchterlony et al. 2006, 2010, 2015), where b(q) = constant was found to be an appropriate description of the sieving curves.

3.3 The Fragmentation–Energy Fan and the Kuz-Ram Model

The Kuz-Ram model (Cunningham 1983, 1987, 2005) has the following basic equations:

$$ P\left( x \right) = 1 - e^{{ - \ln \left( 2 \right)\left( {x/x_{50} } \right)^{n} }} $$

(19a)

$$ x_{50} = A\frac{{Q^{1/6} (115/E)^{19/30} }}{{q^{4/5} }} {\text{in}}\,{\text{cm }} $$

(19b)

with an equation for the rock mass factor A and

$$ n = f\left( {{\text{blast}}\,{\text{geometry}},\, {\text{rock}}\, {\text{mass}}\, {\text{and}}\,{\text{delay}}\, {\text{precision}}\, {\text{but}}\, {\text{not}}\, {\text{specific}}\, {\text{charge} \,{q}}}\right) $$

(19c)

Here Q (kg) is the (average) weight of the charge in a single hole and E (%) the weight strength of the explosive. In the 2005 version of the Kuz-Ram model, A also includes a dependence on delay time, for example. If one sets x = x ₈₀ and P = 0.8, etc. in Eq. 19a, one gets

$$ \begin{aligned} n & = \frac{{\ln \left[ {\ln \left( 5 \right)/\ln \left( 2 \right)} \right]}}{{\ln \left( {x_{80} /x_{50} } \right)}} \\ & = 0.842/\ln \left( {x_{80} /x_{50} } \right) {\text{or}} \\ \end{aligned} $$

(20a)

$$ \begin{aligned} n & = \frac{{\ln \left[ {\ln \left( 2 \right)/\ln \left( {5/4} \right)} \right]}}{{\ln \left( {x_{50} /x_{20} } \right)}} \\ & = 1.133/\ln \left( {x_{50} /x_{20} } \right) \\ \end{aligned} $$

(20b)

whichever ratio one prefers to use. Figure 1 shows log–log plots of the percentiles x ₂₀, x ₅₀ and x ₈₀ from Otterness’ et al. (1991) 29 blasts with 2–4 holes in a limestone quarry. Figure 13 gives more x _P lines. As illustrated in Fig. 20, the quantities ln(x ₈₀/x ₅₀) = ln(x ₈₀) − ln(x ₅₀) and ln(x ₅₀/x ₂₀) = ln(x ₅₀) − ln(x ₂₀) correspond to different vertical distances in the figures that should stay constant and independent of q if n is to be independent of q.

For Eqs. 20a, 20b to be independent of q would require that the power fit lines for all three percentiles x ₂₀, x ₅₀ and x ₈₀ have identical slopes in the log–log diagram, i.e., have the same q exponent and be parallel. This may be the case for x ₂₀ and x ₅₀ in Fig. 1 but certainly not for x ₈₀. Furthermore, Eqs. 20a, 20b then require that the distance between x ₈₀ and x ₅₀ lines in Fig. 1 stays constant and in an exact proportion to the distance between the x ₅₀ and x ₂₀ lines.

Neither is the case. Evaluating Eqs. 20a, 20b shows that n ≈ 0.8 independent of q would describe reasonably well the fragment size distribution in the 20–50% percentile range but that n in the 50–80% range would decrease from n ≈ 1.3 when q = 0.4 kg/m³ to n ≈ 0.8 when q = 1.2 kg/m³. The data of Otterness et al. (1991) thus imply both that the Rosin–Rammler distribution is not an adequate description of the sieving curves from their bench blasting tests and that an n value that does not depend on q is an inadequate description of the energy dependence of the fragmentation. The same conclusions hold for most of the fragmentation–energy fan plots presented in this paper.

3.4 Generalization of the Fragmentation–Energy Fan

In the generalization of the x ₅₀-equation of the Kuz-Ram model (Ouchterlony 2009b), dimensional analysis was used to define a more general blast energy descriptor than q, see Eqs. 27 and 30a for cylinders and bench blasts, respectively, in that paper. In slightly different forms

$$ x_{50} /D = A\frac{{\left[ {\pi /k \cdot \left( {L/D} \right)} \right]^{1/3} }}{{\left( {q \cdot e \cdot B^{0.400} } \right)^{\alpha } }} $$

(21a)

or

$$ x_{50} /B = A\frac{{\left[ {\left( {H/B} \right)\left( {S/B} \right)/k} \right]^{1/3} }}{{\left( {q \cdot e \cdot B^{0.400} } \right)^{\alpha } }} $$

(21b)

where k is a fragment shape factor. Here q·e·D ^0.400 is a dimensional blast energy descriptor, but derived from the dimensional analysis. e is the explosive energy (heat of explosion) per unit mass, so that the product q·e is the energy concentration in the rock or explosive energy input per unit rock volume, the same as used in Fig. 17. Since the explosive type is constant for each group of data analyzed previously, except the Bårarp field tests in Sect. 2.7, the energy is hidden in the A factor and analyzing the data as function of q is equivalent of doing it as function of q·e. The scaling factor D ^0.400 is related to the factor Q ^1/6 in the Kuz-Ram Eq. 19b for x ₅₀.

To use a non-dimensional fragment size descriptor in the present work, e.g., x/D (cylindrical specimens) or x/B (bench blasting), would be a first step of generalization. The mortar cylinders of Johansson (2008) and Johansson and Ouchterlony (2011) were of constant size, D = 140 mm, so introducing x/D would only shift the fragmentation–energy fans in Figs. 2 and 4 vertically by a constant amount −log(D) but not change the slopes of individual lines nor the position of the focal point value q ₀.

The other cylinders blasted in Fig. 6, 7, 8, 9 and 10 were of varying diameter but with roughly constant linear charge concentration Q/L (kg/m). Thus, introducing the non-dimensional size variable x/D makes sense. If we do this for the Hengl amphibolite data in Table 17 and Fig. 6 we obtain Fig. 23. The parameter values are given in Table 11. The primed quantities refer to the eqn x _P/D = $A^ \prime / q ^ {\alpha^ {\prime}_{p}}$for non-dimensional fragment size.

Fig. 23

Non-dimensional fragment sizes x _P/D for Hengl amphibolite cylinders versus specific charge q (Grasedieck 2006)

Table 11 shows that the corresponding x _P/D lines have flatter slopes (lower exponents), all by the same amount α _P − α _P′ = 0.496 and the ratio A/A′ ≈ 167 is constant too. This means that α ₃₅ − α ₂₀ = α ₃₅′ − α ₂₀′, etc. for other subscript combinations. This could be understood in the light that the specific charge for the cylinders is defined by q = (Q/L)/[π/4·D ²] where the linear charge concentration Q/L is roughly constant or the inverse that D = const./√q. Then a division of x by D amounts to a division of A/$q ^ {\alpha_{\text{p}}}$ by q ^−0.5, i.e., a lowering of the q exponent by about 0.5.

Table 11 also shows estimates of the focal point coordinates (x ₀, q ₀). These were calculated as the average value of all possible intersection points between the x _P lines for P = 20, 35, 50, 65 and 80%. Five lines create ten intersection points. Note that despite making x _P non-dimensional, q ₀ remains exactly the same. Consider two lines with different A and α values distinguished by subscripts 1 and 2. Then q ₀ is given by the expression $q_{0} = \, \left( {A_{1} /A_{2} } \right)^{{1/(\alpha_{1} - \alpha_{2} )}} \quad {\text{and}}\quad \, q_{0}^{{\prime }} = \, \left( {A_{1}^{{\prime }} /A_{2}^{{\prime }} } \right)^{{1/(\alpha_{1}^{{\prime }} - \alpha_{2}^{{\prime }} )}}.$ By the arguments in the preceding paragraph, the two expressions become identical and q ₀′ = q ₀. It also follows that if x is divided by a factor D ^β where β is an arbitrary but constant number the same equality results.

Checking for the other cylinder tests reported in Sects. 2.2 and 2.3 shows that α _P − α _P′ is constant for each test but lies in the range 0.45–0.59, i.e., differs somewhat from test to test. This shift to lower exponent values or slopes in log–log space is also associated with smaller r ² values even if very little else has changed. This means that a maximal r ² value may not be the best criterion for determining if x/D is a better response variable than x.

The purpose of generalizing the fragmentation–energy fans is to see whether the data as a function of specific charge could be represented in one diagram for different charge or blast sizes, see discussion in Ouchterlony (2009b). Unfortunately there are not many references where such tests have been made at the same time but one is Rustan and Naarttijärvi (1983), which is also described in Rustan et al. (1983).

They blasted square magnetite mortar slabs of size 100 × 1200 × 1200 mm. The mortar was made from 13% cement, 74% magnetite and 13% water. It had the following properties: Young’s modulus 6 GPa and UCS = 12.1 MPa. The slabs had holes drilled through the H = 100 mm thickness. The ratio S/B = 2 was kept while testing a series of burdens: 25, 35, 45, 55 and 65 mm. The charges were PETN cord of different loads depending on the hole diameter: Q/H = 1 g/m in Ø3-mm holes, 3 g/m in Ø4-mm holes and 5 g/m in Ø5-mm holes. The geometry is shown in Fig. 24.

Fig. 24

Geometry of single-hole slab blasting tests of Rustan and Naarttijärvi (1983)

Rather than using the actual breakage volume, which varies substantially (Ouchterlony and Moser 2013), an equivalent or nominal specific charge is defined as q′ = Q/(B·S·H) = (Q/H)/2B ². The Swebrec function fits the sieving curve data very well with r ² > 0.997. The x _P-data and the regression line data for x _P = $A / q ^ {\alpha_{p }}$ are given in Table 28. These regression line data and those for ${x_{\text{P}}{^ \prime}}$ = x _P/(B/45) and the dimensional alternative x _P″ = x _P/(B/45)^β, c.f. comment after Eq. 21b, for which the mean r ² value is highest, β = 0.543, are given in Table 12. The average burden during the tests, B _ave = 45 mm, has been used to normalize the data. The r ² values in the right hand column are the highest for every P value in the table, but this is slightly misleading since for P = 20, 35 and 50% r ² is the highest for the B-exponent β ≈ 0.60, for P = 65% for β ≈ 0.52 and for P = 80% for β ≈ 0.48.

The last line with data in Table 12 verifies that the focal coordinate q ₀ does not change with the division of the x _P-data by (B/45)^β. In this sense the tendency for the x _P lines to meet at a focal point has not changed. The fragmentation–energy fan for this alternative is shown in Fig. 25. The crosses in this figure denote the original positions of the x _P points shot with constant burden B = 25 mm but different Q/H values, bold data in Table 31, i.e., the original data without division by the factor (25/45)^0.543 ≈ 0.73.

Fig. 25

Fragment sizes x _P/(B/45)^β for slab blasting test versus specific charge q

The fits in Fig. 25 suggest that a function of the form x _P/B ^β = A/q ^α, which can also be written as

$$ x_{P} /B = \frac{A}{{\left( {qB^{{\frac{1 - \beta }{\alpha }}} } \right)^{\alpha } }} = \frac{A}{{\left( {qB^{{\beta^{{\prime }} }} } \right)^{\alpha } }} $$

(22)

and which basically is the same functional relation as the dimensional analysis result, Eq. 21b, could represent the Rustan and Naarttijärvi (1983) data. However, this cannot be assessed in practice since there is a strong collinearity of q and B in the data that inflates the variance of the exponents β′ and α, leading to statistically nonsignificant, and physically unsound, solutions. Larger data sets are required to reach further, see Sanchidrián and Ouchterlony (2016).

4 Conclusions

We have shown that blast fragmentation data in the form of percentile fragment sizes x _P as function of specific charge q form a set of straight lines in a log–log diagram that tend to converge on a common focal point (x ₀, q ₀). This phenomenon is quite clear for single-hole shots in specimens of virgin material, and it is called the fragmentation–energy fan. Low specific charge values, which give a dust and boulders fragmentation and high specific charge values for which fragmentation mechanisms like spalling occur, give data that do not fall on the fan lines.

Field data from bench blasting with several holes in single or multiple rows in rock give data that on average form fragmentation–energy fans and in several presented cases may be interpreted to do so, at least partially and especially if a focal point at infinity (parallel fan lines) is included.

The fan behavior has several consequences. Firstly, the slopes of the fan lines −α _P in log(x _P) versus log(q) space depend only on the P value: α _P = α(P) for a given blasting setup. Secondly, an inversion of α(P) gives a direct, linear transformation between the specific charge, or powder factor, or explosive specific energy dependence of x _P and the sieving curve function P(x) at a given energy level and vice versa. This sieving function is of a preferred type in which two-dimensionless size ratios are used, e.g., P[ln(x _max/x)/ln(x _max/x ₅₀)]. The Swebrec function is of this type, and it follows the fan behavior when the undulation parameter b is constant and does not depend on q.

For the Swebrec function, the slopes function α(P) is given explicitly and it fits the measured data quite well in the given examples of free and confined mortar cylinders. One expects that, when blasting under the same conditions except for variations in specific charge q, blasting harder in general cannot produce less fines. It is shown that for the Swebrec function this requires that b is constant. This confirms earlier results that were obtained when building KCO design curves for quarry blasting. The constancy of b is not obvious, even when working under well controlled experimental conditions. In this sense the fragmentation–energy fan represents an idealized, scatter-free fragmentation behavior.

The existence of the fragmentation–energy fan contradicts two basic assumptions of the Kuz-Ram model: (1) that the RR function reproduces the sieving data well and (2) that the uniformity index n = constant and independent of q. This rather supports the view that the two issues of deriving fragment size prediction formulas and choosing the form of the size distribution function should be separated. The best way to solve the first issue is to formulate the prediction formulas in terms of a sufficient number of percentile fragment sizes x _P.

It was found that the focal point value q ₀ is quite insensitive to simple data transformations. This supports the use of non-dimensional fragment sizes by dividing the size by a characteristic length. This has been done successfully, the non-dimensional fragment sizes also displaying the fan-like pattern. An attempt is made to generalize the fragmentation–energy fans to include an energy term with an explicit size scaling factor dependence that was suggested by earlier dimensional analysis. This generalization seems to require a larger amount of data, with independent variations of specific charge and breakage dimension.

The article contains several tables of fragment size data in "Appendix", mainly x ₂₀, x ₃₅, x ₅₀, x ₆₅ and x ₈₀ that are not accessible in any report. The purpose is to let the reader be able to test the fragmentation–energy fan concept or his/her own ideas about how blast fragmentation data should be best presented.

Appendix: Sieving data

See Tables 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 and 31.

Table 31 Percentile sizes x _P, P = 20, 35, 50, 65 and 80%, in mm for slab blasts, data in Rustan and Naarttijärvi (1983)