Skip to main content
SpringerLink
Log in

Carnot’s theory of transversals and its applications by Servois and Brianchon: the awakening of synthetic geometry in France

  • Published:
Archive for History of Exact Sciences Aims and scope Submit manuscript

Abstract

In this paper we discuss in some depth the main theorems pertaining to Carnot’s theory of transversals, their initial reception by Servois, and the applications that Brianchon made of them to the theory of conic sections. The contributions of these authors brought the long-forgotten theorems of Desargues and Pascal fully to light, renewed the interest in synthetic geometry in France, and prepared the ground from which projective geometry later developed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig.15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32
Fig. 33
Fig. 34
Fig. 35
Fig. 36
Fig. 37
Fig. 38
Fig. 39
Fig. 40
Fig. 41
Fig. 42
Fig. 43

Similar content being viewed by others

Notes

  1. See (La Hire 1673, 1685), (L’Hospital 1707, Book VI), (Le Poivre 1704).

  2. We have in mind essentially (Poncelet 1822), see below.

  3. In the late eighteenth century geometry appeared divided into two main branches: analytic geometry, and pure, or synthetic, geometry. Roughly speaking the first referred to the Cartesian method of coordinates, used equations, algebraic analysis, and infinitesimal calculus in order to reach the solution of proposed problems; the second, which had its roots in the methods of the ancient Greeks, privileged geometrical reasoning on the figure, and (mainly) used proportions rather than equations. For the “rivalry” between analytic and pure geometry in the late eighteenth century see (Chemla 1998), and for a broader overview of the history of analytic/synthetic distinction we refer to (Lorenat 2015a), (Lorenat 2015b).

  4. Most likely Poncelet was referring to the Menelaus–Ptolemy theorem, see Sect. 3.2.

  5. Poncelet was referring to (Brianchon 1806, 1810b), see Sect.  5.

  6. Poncelet was referring to the several notes and memoirs concerning the Geometry of the ruler, which were published in these journals between 1810 and 1820; in particular, the papers by Servois and Gergonne appeared in the Annales, here commented in Sect. 5 and 6.

  7. For an in-depth analysis of the efforts made by Carnot to import into pure geometry the generality of analysis, we refer to (Chemla 1998).

  8. Since Brianchon wanted to compare his own methods with Newton’s, these will be expounded in an “Appendix” to this paper.

  9. The question of the influence of Brianchon’s works on Poncelet’s early research will be investigated in a forthcoming paper devoted to an in-depth study of the notebooks that Poncelet composed during his captivity in Saratov (Russia).

  10. For more information on this subject see (Langins 1990). We recall that Poncelet also attended the École polytechnique and the École d’Application de l’artillerie et du génie at Metz.

  11. With this term Monge referred to architects, engineers, but also painters and engravers.

  12. Monge did not use these terms, they were introduced by F.-J. Servois (1811b, 337), and J. D. Gergonne (1813a, 297) respectively, see Sects. 4, 5; we adopt them since now for convenience.

  13. That is by considering a conic section as projections of the circle.

  14. Monge took for granted that the curve of contacts was a plane curve, this was proved in (Brianchon 1806, Art. XIV).

  15. We note in passing that this concept, which was already present in Kepler’s treatment of conic sections (Del Centina 2016b), and in Desargues’ Brouillon project, was central in Boscovich’s (1754), who first tried to make it operational through a series of rules (canons), see (Del Centina, Fiocca 2018a, 2018b).

  16. An algebraic identity which holds in the real case extends over complex numbers, see for instance (Bourbaki 1960, 131).

  17. For a thorough discussion of the subject of generality in pure geometry in the early nineteenth century we refer to (Chemla 2016, 56–70).

  18. Problems, and solutions deemed worthy, were published in the journals of the School.

  19. For a complete biography see (Gillespie 1971), (Dhombres J. and N. 1997).

  20. This argument has been discussed in (Chemla 1990, 1998), and (Nabonnand 2011).

  21. We refer to (Chemla 1998) and to (Nabonnand 2008) for some detail.

  22. Carnot’s approach was later criticized by Poncelet, see (Nabonnand 2008,39–42).

  23. “Lettre du cit. Carnot, membre de l’Institut national, ministre de la guerre, au cit. Bossut, membre de l’Institut national examinateur du corps di génie”, dated “30 fructidor an 8 de la république français”, 16th September 1799 (Bossut 1800, vol. 2, 401–421).

  24. See (Chemla 1990, 531–532).

  25. See (Taton 1951, 1955), and (Del Centina 2020).

  26. Actually this theorem was not completely new, see footnote 46 (Sect. 6).

  27. In the Essai of 1806, Carnot perfected the definition calling complete quadrilateral the assemblage of four straight lines joining four points in a plane, ordered at will, and then passing from the first to the second, from the second to the third, from the third to the fourth, and from the fourth to the first. Carnot remarked that quadrilaterals can have three different forms: that “ordinaire”, as ABDC, that he named of first kind; that “à angle rentrant”, as AFDG, that he named of second kind; and that “qui a la forme de deux triangles opposes par le sommet”, as BFCG, that he named of third kind.

  28. We note in passing that Brianchon applied this latter in order to prove the theorem on the circumscribed hexagons to a conic section, which bears his name, see Sect. 5.

  29. This theorem was known to Apollonius (Conics, III, props.17–21), see also Sect. 7.4. For future discussion we also recall that Newton used the chords theorem in order to get the important results on conic sections he presented in the fifth section of the first book of the Principia, and in particular to determine the conic sections subject to five conditions (see the “Appendix”). We also note that L’Hospital and J. Stirling recognized its fundamental value for the theory of conic section. For a history of this theorem, and a discussion of the above questions, see (Del Centina, Fiocca 2020).

  30. Carnot referred to Newton’s Enumeratio Linearum Tertii Ordinis, appended to (Newton 1704), see also (Guicciardini 2009, 117–121).

  31. Likely by “etc.” he meant some of the authors quoted in the Dissertation preliminaire.

  32. This theorem re-emerged, also in the general form for conic sections, in the following years. It had, with its dual, a not secondary role in the history of polarity; see later on.

  33. See, Nouveaux Mémoires de l’Académie Royale de sciences et belles lettres, 1776, pp. 265–283, and pp. 284–311.

  34. Annibale Giordamo, was born in S. Giuseppe d’Ottajano, a small town very close to Naples. He was seventeen when he presented his paper. Carnot believed “di Ottajano” to be a noble patronymic, and, as we will see, this led Brianchon, as well as other French mathematicians, to make the same mistake.

  35. See, Memorie di matematica e fisica della Società Italiana, IV, 1788, pp. 4–17, and pp. 201–205.

  36. He was referring to (Simson 1776), published posthumously and containing a work on Pappus’ porisms.

  37. The works which Carnot referred to are (Stewart 1763, 1746).

  38. Namely the Pappus three lines problem.

  39. To denote these points Carnot actually used a quite complicated notation, but we have not followed him.

  40. The hexagon ABEDCF in Carnot’s figure 162 corresponds to the hexagon AECDFB in figure 82 in (Simson 1735).

  41. Although in the long preface to his book Carnot mentioned Maclaurin, and quoted Simson in the text, it seems that he was unaware of (Maclaurin 1748) and (Simson 1735), in which a synthetic proof of Pascal’s was given, see (Del Centina 2020).

  42. We will return to this in the next section.

  43. For the second part, and a discussion on the teaching in the Artillery schools, we refer to (Aebischer, Longuereau 2010).

  44. For Servois’ contribution to the theory of differential operator see (Bradley 2002).

  45. Servois used to label relevant equations by capital letters.

  46. Servois quoted Art. CLV (Proposition I) of the fourth volume of Bernoulli’s complete works (1742). It is worth noting that Bernouilli considered only the case in which the chosen point is inside the triangle, and proved the theorem by using only the similarity of triangles.

  47. “Sont deux diagonales homologues de deux quadrilatères équiangles”, Servois’ words.

  48. Servois adopted the definition given by Carnot.

  49. It is this proof that was inserted into (Carnot 1806, 92–93).

  50. For the history of this theorem see (Mackay, 1892).

  51. This was the third of three propositions announced in 1804 by M. Livet (instructor at the École) in the note Du contact des surfaces coniques avec les surfaces du second degré, whose (analytical) proofs were later published in the Journal. de l’École polytechnique in 1806. Brianchon’s paper appearing in the same issue was inserted immediately after that of Livet.

  52. See Sect. 3.3.

  53. Curiously enough, Brianchon denoted the projections of points L, M, N, l, m, n, by the same upside down letters, which cannot be reproduced here, thus we have used the same letters but in bold font.

  54. We wonder if Brianchon realized that he had proved Desargues’ theorem on homological triangles, and if he was aware of what was already proved by Servois.

  55. The only difference between Carnot’s original statement and Brianchon’s, is the change in meaning of points C and E; compare Fig. 17a with Fig. 8a.

  56. Oddly enough Brianchon did not remark that the triangles DEF and ABC are in perspective with respect to P, and so the points H, I, k are necessarily collinear, that is k belongs to the straight line HIK; similarly, one can see that also i, h lie on HIK. Thus we presume that he did not know Desargues’ theorem on homological triangles.

  57. Since the point P through which pass all contact chords is the “pole” of the straight line HI, we observe that the “pole-polar” property is implicitly stated. We will return to this later on.

  58. Brianchon will develop this topic in (1807), see below.

  59. In this regard it is interesting to read the letter that Brianchon sent to Hachette from Toledo (Spain) on April 1810, see below.

  60. For this construction see also Sect. 5.3.

  61. This name indicated the surface described by all straight lines (generators) that lean on three skew given straight lines (directive lines), which is the double ruled surface also known as one-sheet hyperboloid.

  62. In a footnote it was indicated “Cl. Ptolemei. Venetiis, 1515, in fol.”. Brianchon’s interest in the history of geometry fully emerged in (1817), see later on.

  63. For a comparison between Ptolemy’s statements of the theorem and Carnot’s see (Chemla 1990, 530–532).

  64. In fact, one can suppose that the given curve is a circle, thus, if the given straight line is l, it is about finding an oblique cone with base the given circle such that a sub-contrary section is parallel to the plane passing through the vertex of the cone and the line l.

  65. See (Poncelet 1862, 387).

  66. He did not say this but obviously he had the following construction in mind: issue from F any two secants as FHG and FLK, intersect GL and KH, GK and HL, then draw the straight line through the two points of intersection; this straight line (XY) intersects the conic section at the contact points of the tangent through F. Clearly XY is the polar of F, see later on.

  67. This means that XY is the polar of F.

  68. Clearly referring to (Carnot 1803, Th. XLV).

  69. That is, the tangent lines to the conic section at the extremities of each chord through P meet on HK.

  70. Brianchon referred to Art. XIII, most likely a misprint.

  71. Brianchon’s “projective view” is indisputable.

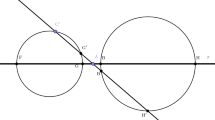
  72. Brianchon denoted the circles and their centres by the same letters.

  73. In fact, OO′ is equal to the radius of C′, and the perpendicular to CC′ issued from m is the polar of C′ with respect to C, but Brianchon omitted to say this.

  74. See (Poncelet 1862, 408).

  75. D. Encontre was a professor at the Faculty of Sciences of the Academy of Montpellier.

  76. Obviously the poles of the given straight lines, but Encontre did not say it.

  77. Likely Servois confused Mdccxxxiii for Mdcccxxviii, so the reference is to (Braikenridge 1733).

  78. It is not clear to us to which proofs Servois was referring to.

  79. It is worth noticing that Poncelet referred to the geometry “cultivée par les modernes” as that which proceeds “par la voie d’intuition” (Poncelet 1817, 143).

  80. (Brianchon 1807, 1810b), see and Sect. 5.2.

  81. J. D. Gergonne was born in Nancy, and he attended the local College, but he was essentially self-taught. In 1792 he enrolled in the Army, and, examined by Lacroix, he was admitted to the Artillery school at Châlon. As Lieutenant he participated in the war of Spain. From 1795, under the influence of Monge, he concentrated on mathematics. Gergonne left the army and became professor of transcendental mathematics at Nimes, then, in 1816, he was appointed professor of astronomy at the University of Montpellier, of which he became rector in 1832. In 1810 he founded the first journal entirely devoted to mathematics, the Annales de mathématiques pures et appliquées, which played a leading role in the development of geometry in France, see (Gerini 2002).

  82. We point out that in this case the three intersection points of the opposite sides lie on the line at infinity.

  83. To do that, Gergonne tacitly admitted that the straight line joining the two intersection points of the two pairs of opposite sides does not meet the circle, see below.

  84. See Annales des mathématiques pures et appliquées, vol. 4 (1813–1814), Questions proposées, p. 193.

  85. This note appeared as “par M. B.***, abonné”. We do not know the reason why this note was published semi-anonymously.

  86. On the contest between Poncelet and Gergonne see (Lorenat 2015c, 551–553).

  87. That is numbered at will.

  88. This is a direct consequence of the law of sines.

  89. In a footnote Poncelet stated exactly Brianchon’s proposition quoting (Brianchon 1817).

  90. See Sect. 3.3. Brianchon took the opportunity to recall that this principle was known to the ancients, who had extended it to the sphere, making it the basis of all their trigonometry; and he referred to the Almagest, and to (Maurolico 1575, 281).

  91. In a footnote Brianchon pointed out that, in 1639, Desargues had printed a treatise on conic sections that no longer existed (1817, 15). A manuscript copy of Desargues’ Brouillon project due to La Hire was found by Chasles in 1845, and an original copy was found in the Biblithèque nationale de France by R. Taton in 1951.

  92. Brianchon’s notation.

  93. It is worth noticing that this means that Brianchon determined C, K as the fixed points of the involution defined on the transversal AB by the opposite sides of the (degenerate) quadrilateral UUXX formed by tangents at U and X (as opposite sides), and UX counted twice (as the other two opposite sides).

  94. To see this, Brianchon observed that the triangles EVX, FUW satisfy the conditions of theorem Λ with respect to C, K respectively; that is he used Desargues’ theorem on homological triangles.

  95. See (Maclaurin 1748, Art. 623).

  96. In a footnote Brianchon pointed out, “Depuis la publication du mémoire cite, je suis parvenu à une proposition plus générale; elle est consignée dans le quatrième volume des Annales de Mathématiques, page 196 et 379”. He was referring to the more general result published in (1814b), see Sect. 6.2.

  97. For a historical account on Poncelet’s porism see (Del Centina 2016a).

  98. Brianchon did not give any reference for the theorem he was referring to, and, as far as we know, it does not appear either in (Carnot 1803) or in (Servois 1804). Gauss knew it already in 1810, and provided an analytical proof of it (Gauss 1873, 391), but it is quite improbable that Brianchon was aware of this. However, the theorem in question seems to have been proposed for the first time by J. T. Connor in the Ladies’ Diary for the year 1795, and two solutions were offered shortly afterwards, see (Leybourn 1817, 291).

  99. We do not know which authors Brianchon was referring to.

  100. As it will be seen in the “Appendix”, in solving the same problems Newton used the chords theorem, which, similarly to Pascal’s hexagon theorem, gives a condition for six point to belong to a conic section, but while in the latter case the six points can be taken at will, in the former four of the six points have to lie on parallel straight lines. Thus, although the chords theorem is sufficient to reach the solution, its use affects the simplicity of the proofs.

  101. Brianchon quote it dated 1662, the year of Pascal’s death.

  102. (Poncelet 1822, xiv). For a discussion and justification of this principle in Poncelet we refer to (Nabonnand 2011, 2015), and (Lorenat 2015a).

  103. See for instance (Lorenat 2015a, b, c).

  104. See the fifth section of the first book of the Principia (Newton 1687, 1729).

  105. Newton referred to it simply writing “ex Conicis”, see (Heath 1896, 95).

  106. On this author see (Raynaud 2020).

  107. English translation extracted from (Newton 1729).

References

  • Aebischer, A.-M., and H. Languereau. 2010. Servois- la géométrie à l’école de l’artillerie. de Franche-Comté: Press Univ.

    Google Scholar 

  • Andersen, K. 2007. The Geometry of an Art, the History of the Mathematical Theory of Perspective from Alberti to Monge. Berlin: Springer.

    MATH  Google Scholar 

  • Bernoulli J. 1742, Opera omnia, tam antea sparsiam edita, quam hactenus inedita, 4 vols., Lousannae & Genevae, M.-M. Bousquet et Sociorum.

  • Blondel N.-F. 1673, Résolution des quatre principaux problèmes d’architecture, Mémoires de l’Académie Royale des Sciences, depuis 1666 jusqu’à 1699, tome 5 (1729), 355–520.

  • Boscovich, R.J., 1754. Dissertatio de transformatione locorum geometricorum, in Elementa Universae Matheseos, vol. 3, (1754), pp. 297–468, Salomoni, Romae.

  • Bosse A. 1648, Manière universelle de Mr. des Argues pour pratiquer la perspective par petit-pied comme le géométral etc., Paris, P. Des-Hayes.

  • Bossut C. 1800, Cours de mathématiques, géométrie et applications de l’algèbre à la géométrie, Nouvelle edition revue et augmentée, 3 vols., Paris, F. Didot.

  • Bourbaki, N. 1960. Éléments d’histoire des mathématiques. Paris: Hermann.

    MATH  Google Scholar 

  • Boyer J. 1894a, Le mathématicien Franc-Comtois François-Joseph Servois, ancien conservateur du musée d’artillerie d’après des documents inédite 1767–1847, Mémoires de la Soc. d’émulation du Doubs, 6e series, 9, 305–328.

  • Boyer J. 1894b, Charles-Julien Brianchon, d’après des documents inédits, Revue Scientifique, 4e série, I, 592–594.

  • Bradley R. E. 2002, The origin of Linear Operator Theory in the Work of François-Joseph Servois, Proceedings of the Canadian Soc. for Hist. and Phil. of Mathematics, 14, 1–21.

  • Braikenridge W. 1733, Exercitatio geometrica de descritione linearun curvarum, Londini, Apud. Ric. Hett, & Joh. Nourse.

  • Brianchon, C.-J. 1806. Sur les surfaces courbes du second degré. Journ. de l’École Polytechniques 6: 297–311.

    Google Scholar 

  • Brianchon C.-J. 1807, Lettre de M. Brianchon, officier d’artillerie, ancien élève de l’École Impériale Polytechnique, Metz, le 3 janvier 1807, Correspondance. sur l’École Polytechnique, 1 (5), 307–311.

  • Brianchon C.-J. 1808, Géométrie, Sur le surfaces gauche du second degré; Solution de M. Brianchon, Correspondance. sur l’École Polytechnique, 1 (10), 434–436.

  • Brianchon C.-J. 1810a, M. Brianchon, officier d’artillerie, à M. Hachette, Tolède, 8 avril 1810, Correspondance. sur l’École Polytechnique, 2 (1), 257–260.

  • Brianchon, C.-J. 1810b. Solutions de plusieurs problèmes de géométrie. Journ. de l’École Polytechniques 10: 1–15.

    Google Scholar 

  • Brianchon, C.-J. 1813. Géométrie de la règle. Correspondance. sur l’École Polytechnique 2 (5): 383–387.

    Google Scholar 

  • Brianchon, C.-J. 1814a. Géométrie. Correspondance. sur l’École Polytechnique 3 (1): 1–4.

    Google Scholar 

  • Brianchon, C.-J. 1814b. Demonstration de premier des deux théorèmes énoncés a la page 196 de ce volume. Ann. de Math. Pure et Appl. 4 (1813–1814): 379–381.

    Google Scholar 

  • Brianchon, C.-J. 1817. Mémoire sur les lignes du second ordre; faisant suite aux recherches publiées dans les Journaux de l’École Polytechniques. Paris: Bachelier.

    Google Scholar 

  • Brianchon, C.-J. 1818. Applications de la théorie des transversal. Paris: Bachelier.

    Google Scholar 

  • Brianchon, C.-J., and J.-V. Poncelet. 1820. Recherches sur la détermination d’une hyperbole équilatère, au moyen de quatre conditions données. Ann. de Math. Pure et Appl. 11 (1820–1821): 205–220.

    Google Scholar 

  • Brianchon, C.-J. 1823. Des courbes de raccordement. Journ. de l’École Polytechniques 12: 187–203.

    Google Scholar 

  • Carnot L. 1801, De la correlation des figures de géométrie, Paris, chez Duprat.

  • Carnot, L. 1803. Géométrie de position, Paris, chez J. Duprat: B. M.

    Google Scholar 

  • Carnot, L. 1806. Mémoire sur la relation qui existe entre les distances respectives de cinq points quelconques pris dans l’espace, suivi d’un Essai sur la théorie des transversales. Paris: Courcier.

    Google Scholar 

  • Chasles M. 1837, Aperçu historique sur l’origine et le développement des méthodes en géométrie, Bruxelles, H. Hayez.

  • Chemla K. 1990, Remarques sur les recherches géométriques de Lazare Carnot, in “Lazare Carnot ou le savant-citoyen”, M. Charnay Ed., Presses de l’Université de la Sorbonne, pp. 525–541.

  • Chemla, K. 1998. Lazare Carnot et la généralité en géométrie. Variation sur le théorème de Menelaus. Revue d’histoire des mathématiques 4: 163–190.

    MathSciNet  MATH  Google Scholar 

  • Chemla K. 2016, The value of generality in Michel Chasles historiography of geometry, in “The Oxford Handbook of Generality in Mathematics and the Sciences”, K. Chemla, R. Chorlay eds., Oxford University Press.

  • Coolidge, J.L. 1968. A history of the conic sections and quadric surfaces. New York: Dover.

    MATH  Google Scholar 

  • Del Centina, A. 2016a. Poncelet’s porism: a long story of renewed discoveries I. Arc. Hist. Exact Sci. 70: 1–122.

    Article  MathSciNet  Google Scholar 

  • Del Centina, A. 2016b. On Kepler’s system of conics in Astronomiae pars optica. Arc. Hist. Exact Sci. 70: 567–589.

    Article  MathSciNet  Google Scholar 

  • Del Centina, A., and A. Fiocca. 2018a. Boscovich’s geometrical principle of continuity, and the “mysteries of the infinity.” Historia Mathematica 45: 131–175.

    Article  MathSciNet  Google Scholar 

  • Del Centina, A., and A. Fiocca. 2018b. “A masterly though neglected work”, Boscovich’s treatise on conic sections. Archive for History of Exact Sciences 72: 453–495.

    Article  MathSciNet  Google Scholar 

  • Del Centina, A. 2020. Pascal’s Mystic hexagram, and a conjectural restoration of his lost treatise on conic sections. Archive for History of Exact Sciences 74: 469–521.

    Article  MathSciNet  Google Scholar 

  • Del Centina A., Fiocca A. 2020, The chords theorem recalled to life at the turn of the eighteenth century, accepted for publication in Historia Mathematica.

  • Desargues G. 1639, Brouillon project d’une atteinte aux evenemens des rencontres du Cone avec un Plan, par L. S. G. D. L. Paris.

  • Descartes R. 1637, La Géométrie. In R. Descartes, “Discours de la Méthode, pour bien conduire sa raison et chercher la vérité dans les sciences etc.”, Leide, Maire.

  • Dhombres, J., and N. . 1997. Lazare Carnot. Paris: Librarie Artheme Fayard.

    Google Scholar 

  • Dupin, Ch. 1819. Essai historique sur les services et les travaux scientifiques de Gaspard Monge. Paris: Bachelier.

    Google Scholar 

  • Gauss C. F. 1873, Werke, vol. 4, Göttingen.

  • Gergonne, J.D. 1813a. Théorie analytique des pôles des lignes et des surfaces du second ordre. Ann. de Math. Pure App. 3 (1812–1813): 293–302.

    Google Scholar 

  • Gergonne J. D. 1813b, Géométrie de la règle. Applications de la doctrine des projections à la démonstration des propriétés des hexagones inscrits et circonscrits aux sections coniques, Ann. de Math. Pure App., 4 (1813–1814), 78–84.

  • Gerini, C. 2002. Les “Annales” de Gergonne: apport scientifique et épistèmologique dans l’histore des mathematiques, Villeneuve d’Ascq. Éd: di Septentrion.

    Google Scholar 

  • Gillespie, C.C. 1971. Lazare Carnot, Savant. Press: Princeton Univ.

    Google Scholar 

  • Heath, T.L. 1896. Apollonius of Perga treatise on conic sections, edited in modern notation, Cambridge. Press: Univ.

    Google Scholar 

  • Langins, J. 1990. The École polytechnique and the French revolution: merit, militarization, and mathematics. LLULL 13: 91–105.

    Google Scholar 

  • La Hire P. 1672, Observations de Ph. De La Hire, Sur les points d’attouchement de trois Lignes droits qui touchent la Section d’un Cone etc., Paris, chez A. Bosse.

  • La Hire P. 1673, Nouvelle méthode en géométrie pour les sections des superficies coniques, et cylindriques, etc., Paris.

  • La Hire P. 1685, Sectiones conicae, in novem libros distributae, Parisiis, apud S. Michallet.

  • L’Hospital 1707, Traité analytique des sections coniques et de leur usage pour la résolution des équations dans les Problèmes tant déterminez qu’indeterminez, Paris, J. Boudot et fils.

  • Leybourn T. 1817, Mathematical questions proposed in the Ladies’ Diary, vol. 3, London, W. Glendinning.

  • Le Poivre J.-F. 1704, Traité des sections du cylindre et du cone, considérées dans le solide et dans le plan, avec des démonstrations simples et nouvelles. Paris, B. Gerin.

  • Lorenat J. 2015a, Die Freude and die Gestalt : methods, figures, and practices in early nineteenth century geometry, PhD thesis, Université Pierre et Marie Curie.

  • Lorenat, J. 2015b. Figures real, imagined, and missing in Poncelet. Plücker, and Gergonne, Historia mathematica 42: 155–192.

    Article  MathSciNet  Google Scholar 

  • Lorenat J. 2015c, Polemics in Public : Poncelet, Gergonne, Plücker, and the Duality Controversy.

  • Mackay, J.S. 1892. History of the Nine-Points Circle. Proc. Edinburg Math. Soc. 11: 19–61.

    Article  Google Scholar 

  • Maclaurin C. 1720, Geometria Organica: sive descriptio linearum curvarum universalis, Londini, G. and J. Innys.

  • Maclaurin C. 1735, A letter from C. Mac Laurin, Math. Prof. Edinburg. F.R.S. to Mr John Machin, Astr. Prof. Gresh. et Secr. R.S. concerning the description of curve lines, communicated to the Royal Society on Dicember 21, 1732. Phil. Trans. of the Royal Soc. of London, 39 (439), pp. 143–165.

  • Maclaurin C. 1748, A Treatise of Algebra in three Parts…to which is added an Appendix concerning the general properties of Geometrical Lines, London, A. Millar and J. Nourse.

  • Maurolico F. 1575, Opuscula mathematica, Venetij, Apud F. F. Senensem.

  • Milne J.J. 1927, Newton’s contribution to the geometry of conics. In “Isaac Newton 1642–1727: a memorial volume edited for the Mathematical Association, by William J. Greenstreet”. London, Bell and Sons, pp. 96–114.

  • Monge G. 1799, Géométrie descriptive, Paris, Baudouin Imprimeur du Corps législatif et de l’Institut national.

  • Monge, G. 1811. Géométrie descriptive. Avec un supplement par M: Hachette, Paris. J. Klostermann fils.

    Google Scholar 

  • Nabonnand P. 2008, Contributions à l’histoire de la géométrie projective au 19e siècle. Document présenté pour l’HDR, hal-010 82207.

  • Nabonnand P. 2011, L’argument de la généralité, chez Carnot, Poncelet et Chasles. Justifier en mathématique, Editions de la maison des sciences de l’homme, Paris, pp. 17–47 (hal-00637385).

  • Nabonnand P. 2015, L’étude des propriétés projectives des figures par Poncelet: une modernité explicitement ancrée dans la tradition, in “Sciences mathématiques 1750–1850” Eds. C. Gilain and A. Guilbausd, CNRS Editions, pp. 381–402.

  • Newton I. 1687, Philosophiae Naturalis Principia Mathematica, Londini, Typis J. Streater.

  • Newton I. 1726, Philosophiae Naturalis Principia Mathematica, Londini, Apud Guil & John Innys.

  • Newton I. 1729, The Mathematical Principle of Natural Philosophy, London, B. Motte.

  • Newton I. 1704, Opticks: Or, A Tratise of the Reflections, Refractions and Colours of Light, etc., London, S. Smith and B. Walford.

  • Pascal B. 1640, Essay pour les coniques, Paris; also in (Pascal 1779, vol. IV).

  • Pascal B. 1654, Celeberrimae Matheseos Academiae Parisiensis, in (Pascal 1779, vol. IV).

  • Pascal B. 1779, Oeuvres de Blaise Pascal, 4 vols, Ed. C. Bossut, La Haye, chez Detune.

  • Poncelet, J.-V. 1817. Réflexions sur l’usage de l’analyse algébriques dans la géométrie: suivies de la solutions de quelques problèmes dépendent de la Géométrie de la règle. Ann. de Math. Pure et Appl. 8: 141–155.

    Google Scholar 

  • Poncelet, J.-V., 1822. Traité des propriétés projectives des figures. Bachelier, Paris. 2nd ed., Gauthier-Villars, Paris, 1865.

  • Poncelet, J.-V. 1862. Applications d’analyse et de géométrie, qui ont servi de principal fondement au Traité des propriétés projectives des figures, vol. 1. Paris: Gauthier-Villars.

    Google Scholar 

  • Poncelet, J.-V. 1864. Applications d’analyse et de géométrie, qui ont servi de principal fondement au Traité des propriétés projectives des figures, vol. 2. Paris: Gauthier-Villars.

    Google Scholar 

  • Raynaud, D. 2020. Mathématiques et architecture : le tracé de l’entasis par Nicolas-François Blondel. Arch. Hist. Exact Sc. 74: 445–468.

    Article  Google Scholar 

  • Sakarovitch J. 2005, Gaspard Monge, Géométrie descriptive, in “Landmark Writings in Western Mathematics 1640–1940”, I. Grattan-Guinnes Ed., Amsterdam, Elsevier.

  • Saint Vincent, G., 1647. Opus geometricum quadraturae circuli et sectionum coni decem libris comprehensum, Antverpiae, apud Ioannem et Iacobum Meursios.

  • Servois, F.-J. 1804. Solutions peu connues de différents problems de géométrie pratique pour server de supplement aux traités e cette science. Paris: Bachelier.

    Google Scholar 

  • Servois, F.-J. 1811a. Solution, avec la règle seulement, du dernier des deux problèmes proposés à la page 259 de ce volume. Ann. de Math. Pure et Appl. 1 (1810–1811): 332–336.

    MathSciNet  Google Scholar 

  • Servois, F.-J. 1811b. Solution du premier de deux problèmes proposes à la page 259 de ce volume, et du problème propose à la page 126 du même volume. Ann. de Math. Pure et Appl. 1 (1810–1811): 337–342.

    MathSciNet  Google Scholar 

  • Simson R. 1723, Pappi Alexandrini Propositiones duae generals, quibus plura ex Euclids Porismatis complexus est, Restitutae a Viro Doctissimo Rob. Simson, Math. Prof. Glasc. Vid. Pappi praefationem ad Lib. 7. Coll. Math. Apollonii de Sectione rationis libris duobus a Clariss. Hallejo praemissam pag. VII et XXXIV, Philosophical Transactions, 11 (1723), pp. 330–340, also in (Simson 1776).

  • Simson R. 1735, Sectionum conicarum libri V, Edinburgi, T. & W. Ruddimannos

  • Simson R. 1776, Roberti Simson, M.D., Matheseos nuper in Academia Glasguensi professoris, Opera quaedam reliqua, etc., Glasguae, R. et A. Foulis Academiae Typographi.

  • Stewart M.1746, Some geometrical theorems of considerable use in the higher part of mathematics, Edinburgh, printed by Sands, Marray and Cochran.

  • Stewart M. 1763, Propositiones geometrcae more veterum demonstratae, Edinburgi, typis Sands, Marray, et Cochran.

  • Taton, R. 1951. L’oeuvre scientifique de Monge. de France: Paris, Press Univ.

    MATH  Google Scholar 

  • Taton R. 1955, L’ “Essay pour les coniques” de Pascal, Revue d’Hist. des Sc. et leurs Appl., 1–18.

  • Taton R. 1962, L’oeuvre de Pascal en géométrie projective, Revue d’Hist. des Sc. et leurs Appl., 15 (3–4), 197–252.

  • Van Schooten F. 1656, Exercitationum mathematicarum libri, Lugd. Batav., J. Elzevier.

  • Whiteside, D.T. 1961. Patterns of mathematical thought in the latter seventeenth century. Arch. For Hist. Ex. Sc. 1: 179–388.

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

I owe heartfelt thanks to the referees for their thoughtful, inspiring, and helpful suggestions that allowed me to improve this paper.

Author information

Authors and Affiliations

  1. Dipartimento di Matematica e Informatica, Via Machiavelli 30, 44121, Ferrara, Italy

    Andrea Del Centina

Authors
  1. Andrea Del Centina
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Andrea Del Centina.

Additional information

Communicated by Jeremy Gray.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix

Newton’s methods for determining the conic sections subject to five conditions

To understand the progress made by Brianchon in finding the conic sections subject to five conditions, we compare them with those used by Newton,Footnote 104 which had their roots in the chords theorem that we mentioned previously in Sect. 3.3.

n = 5. Without going into detail, we can say that Newton gave two solutions, one through his Lemma 20, and the other via his organic construction; both depending on the chords theorem.

In the other cases Newton resorted to a special case of the chords theorem, which, see Fig 44. 

Fig. 44
figure 44

a Diagram for the special case of the chords theorem. b This is an enhanced version of the figure provided in (Newton 1687, 84)

Full size image

44a, can be statedFootnote 105: (#) Let two tangents to a conic section be given, PO, QO, touching the curve at P, Q and intersecting each other at O, together with two chords parallel to them, Rr, R′r′, meeting at J. Then

$$\frac{P{O}^{2}}{Q{O}^{2}}=\frac{RJ\times Jr}{R{^{\prime}}J\times r{^{\prime}}J}$$

n = 4. Newton proceeded as follows. He let B, C, D, P be the given points, and IH be the given straight line, which he supposed cut at points I and H by the straight lines CP and BD respectively (Fig. 44b). By applying proposition #, Newton proved that the point of tangency A on IH satisfies the equation

$$\frac{H{A}^{2}}{A{I}^{2}}=\frac{XH\times HY}{BH\times HD}\left(=\frac{CG\times GP}{DG\times GB}\right)\cdot \frac{BH\times HD}{PI\times IC}=\frac{XH\times HY}{PI\times IC}$$

and remarked that A can fall either between H and I, or outside this interval, that is to say that the problem has two solutions.

n = 3. Newton named B, C, D the given points, G the point where the two given straight lines GP and GA meet, and P, A, the points of tangency. He drew the straight line BD, which intersects GP at H and GA at K (Fig. 45a), and called R the point where BD meets the chord of contacts PA. Then he drew the straight line CD, which cuts GP at I, and GA at L; and called S the point where CD meets the chord of contacts PA. By applying proposition (#), he showed that R satisfies the equation

$$H{R}^{2}\times BK\times KR=K{R}^{2}\times BH\times HD$$

and S satisfies the equation

$$I{S}^{2}\times CL\times LD=L{S}^{2}\times CI\times ID$$
Fig. 45
figure 45

a Enhanced version of Newton’s figure for the problem n = 3, which includes one of the sought conic sections. b Diagram for the discussion of the case n = 0

Full size image

He also proved that R, S, P, A are collinear. So if R, S are determined on BD and CD by the above equations, the contact chord, coinciding with SR, is known, and hence also the points of contact P and A are known. Then Newton observed that R may lie between H and K, or outside; and S may lie between I and L, or outside. By observing this Newton implicitly said that there are four conic sections satisfying the required conditions, which can be drawn by resorting to the case n = 5.

We point out that in the cases n = 4, 3, Newton tacitly supposed that the straight line XY to intersect the sought-for conic section. It is worth noticing that in the third edition of the Principia (1726, 87), Newton claimed that the equations to which he was led for the determination of the points of tangency still hold even if XY does not intersect the curve. With this Newton implicitly applied the principle of continuity in the form of permanence of algebraic relations.

n = 2, 1. To treat these cases Newton introduced certain transformations in the plane of the figure which allowed him to solve the problem in a simpler situation, and then to claim the solution of the general problem by applying the inverse transformation. This procedure has been thoroughly discussed in (Milne 1927) and (Whiteside 1961), so we limit ourselves to pointing out a few things. In case n = 2, if B, C are the given points, A is the point where two among the given straight lines meet, and O is the point where the third straight line meets the straight line BC, Newton transformed the given figure in such a way that the first two straight lines become parallel, and the third becomes parallel to the transformation of BC. In case n = 1, Newton transformed the quadrilateral formed by the given straight lines into a parallelogram. Afterwards, in both cases he applied theorem (#) to get the points of tangency.

We observe that in case n = 2 the transformation applied by Newton maps the straight line AO in the line at infinity, while in case n = 1 the transformation applied maps the straight line joining the intersection point of two given lines, say A, with the intersection point of the other two, say O, in the line at infinity. Hence, in both cases the transformations applied by Newton are equivalent to making a perspective of the given figures into a plane parallel to the plane through the point of projection and the straight line AO.

In agreement with Whiteside (1961, 288), we believe that Newton may have drawn inspiration from (La Hire 1673), where similar transformations are introduced, and applied in the study of conic sections. We also point out that La Hire was led to study questions of tangency (La Hire 1672) by Abraham Bosse, an engraver and friend to Desargues, who was interested in solving certain masonry problems connected with the construction of rampant arches. These problems, in fact, require an arc of conic section to be drawn that passes through given points and is tangent to certain straight lines. In this regards, it is interesting to note that Brianchon (1817, 52) instead of (La Hire 1672) quoted. (Blondel 1673),Footnote 106 in which the same problems were treated.

Moreover, it is worth noting that although Newton did not directly resort to the projection method he showed he was aware of it. In fact, after having proved Lemma 22 (1687, 87), Newton wrote “For as often as two conic sections occur…any of them may be transformed…into a circle. So also a right line and a conic section may be transformed into a right line and a circle”.Footnote 107 Enunciations very close to one of the projection principles that we have seen Brianchon put forward.

n = 0. Newton’s method for this case is very long. He needed three more lemmas, the second of which was already known to Apollonius (Conics, III, prop. 42), and some corollaries. We omit all these preliminaries, referring the reader directly to the Principia, or to (Milne 1927). Then, to find the conic section tangent to the five given straight lines, Newton first determined the centre of the curve. Let ABC, BCF, GCD, FDE, EA be the five tangents, and consider the quadrilateral ABFE circumscribed to the sought curve (Fig. 45b). By means of the third lemma, he proved that the straight line joined the midpoints M, N of the diagonals AF, BE is a diameter of the sought curve, and that the same holds true for the straight line joining the midpoints P, Q of the diagonals BD, GF of the circumscribed quadrilateral BGDF. Then the point O intersection of these two diameters is the centre of the sought-for curve. Afterwards he drew LK parallel to BC at such a distance that O is in the middle between LK and BC, K, L being the points where it intersects the tangents FDE and GCD, and denoted R the point where FL meets CK. By a corollary of the second lemma, he proved that the straight line RO meets the tangents CF, KL at the contact points. Thus, determined the five points of contact, the problem was reduced to case n = 5.

As we have seen in Sect. 7.4, Brianchon quoted Newton only when treating the cases n = 0, 1, and to underline that his method was different from Newton’s, but he certainly knew how Newton handled the other cases, and we are left to wonder whether he recognized any similarity with his arguments.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Del Centina, A. Carnot’s theory of transversals and its applications by Servois and Brianchon: the awakening of synthetic geometry in France. Arch. Hist. Exact Sci. 76, 45–128 (2022). https://doi.org/10.1007/s00407-021-00276-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00407-021-00276-1

Search

Navigation