Skip to main content
SpringerLink
Log in

A finite element formulation using four-unknown incorporating nonlocal theory for bending and free vibration analysis of functionally graded nanoplates resting on elastic medium foundations

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

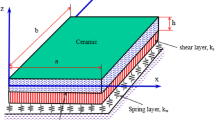
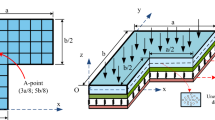
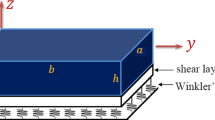
A finite element model using four-unknown shear deformation theory integrated with the nonlocal theory is proposed for the bending and free vibration analysis of functionally graded (FG) nanoplates resting on elastic foundations. The present study developed the four-node quadrilateral element using Lagrangian and Hermitian interpolation functions for analysis of the membrane and bending displacement fields of FG nanoplates. Such a finite element formulation is suitable to investigate for the FG nanoplates resting on the elastic medium foundation with the stiffness matrices, the mass matrices and the load vectors using the second derivatives. The material properties of FG nanoplates are assumed to vary through the thickness direction by a power rule distribution of volume-fractions of the constituents. The equation of motion for FG nanoplates resting on the elastic foundation is obtained through Hamilton’s principle. Several numerical results are presented to demonstrate the accuracy and reliability of the present approach in comparison with other existing methods. In addition, the effects of geometrical parameters, material parameters, nonlocal parameters on the static bending and the free vibration responses of the nanoplates is also investigated in detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Wang Q, Varadan V (2006) Wave characteristics of carbon nanotubes. Int J Solids Struct 43(2):254–265

    MATH  Google Scholar 

  2. Nicolas GH, Anthony TP (1997) Heterogeneous atomistic-continuum representations for dense fluid systems. Int J Mod Phys C 8(4):967–976

    Google Scholar 

  3. Eringen AC (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phy 54:4703–4710

    Google Scholar 

  4. Eringen AC (2002) Nonlocal continuum field theories. Springer, New York

    MATH  Google Scholar 

  5. Ansari R, Sahmani S, Arash B (2010) Nonlocal plate model for free vibrations of single-layered graphene sheets. Phys Lett A 375(1):53–62

    Google Scholar 

  6. Arash B, Wang Q (2012) A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphenes. Comput Mater Sci 51(1):303–313

    Google Scholar 

  7. Asemi SR, Farajpour A (2014) Decoupling the nonlocal elasticity equations for thermomechanical vibration of circular graphene sheets including surface effects. Phys E 60:80–90

    Google Scholar 

  8. Jalali SK, Jomehzadeh E, Pugno NM (2016) Influence of out-of-plane defects on vibration analysis of graphene: molecular dynamics and non-local elasticity approaches. Superlattice Microst 91:331–344

    Google Scholar 

  9. Ahababaei R, Reddy JN (2009) Nonlocal third-order shear deformation plate theory with application to bending and vibration of plate. J Sound Vib 326(1–2):277–289

    Google Scholar 

  10. Pradhan SC, Murmu T (2009) Small scale effect on the buckling of single-layered graphene sheets under biaxial compression via nonlocal continuum mechanics. Comput Mater Sci 47(1):268–274

    Google Scholar 

  11. Reddy JN (2010) Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int J Eng Sci 48(11):1507–1518

    MathSciNet  MATH  Google Scholar 

  12. Prandhan SC, Phadikar JK (2011) Nonlocal theory for buckling of nanoplates. Int J Struct Stabil Dynam 11(3):411–429

    MathSciNet  MATH  Google Scholar 

  13. Farajpour A, Danesh M, Mohammadi M (2011) Buckling analysis of variable thickness nanoplates using nonlocal continuum mechanics. Phys E 44(3):719–727

    Google Scholar 

  14. Murmu T, Adhikari S (2011) Nonlocal vibration of bonded double-nanoplate-systems. Compos B Eng 42(7):1901–1911

    Google Scholar 

  15. Aksencer T, Aydogdu M (2012) Forced transverse vibration of nanoplates using nonlocal elasticity. Phys E 44(7–8):1752–1759

    Google Scholar 

  16. Satish N, Narendar S, Gopalakrishnan S (2012) Thermal vibration analysis of orthotropic nanoplates based on nonlocal continuum mechanics. Phys E 44(9):1950–1962

    Google Scholar 

  17. Shen ZB, Tang HL, Li KK, Tang GJ (2012) Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal Kirchhoff plate theory. Comput Mater Sci 61:200–205

    Google Scholar 

  18. Hashemi SH, Zare M, Nazemnezhad R (2013) An exact analytical approach for free vibration of Mindlin rectangular nano-plate via nonlocal elasticity. Compos Struct 100:290–299

    Google Scholar 

  19. Fazelzadeh SA, Ghavanloo E (2014) Nanoscale mass sensing based on vibration of single layered grapheme sheet in thermal environments. Acta Mech Sin 30(1):84–91

    MathSciNet  MATH  Google Scholar 

  20. Ke LL, Wang YS, Yang J, Kitipornchai S (2014) Free vibration of size-dependent magneto-electro-elastic nanoplates based on the nonlocal theory. Acta Mech Sin 30(4):516–525

    MathSciNet  MATH  Google Scholar 

  21. Malekzadeh P, Golbahar HMR, Shojaee M (2014) Nonlinear free vibration of skew nanoplates with surface and small scale effects. Thin Wall Struct 78:48–56

    Google Scholar 

  22. Craciunescu CM, Wuttig M (2014) New ferromagnetic and functionally graded shape memory alloys. J Optoelectron Adv Mat 5(1):139–146

    Google Scholar 

  23. Fu Y, Du H, Zhang S (2003) Functionally graded TiN/TiNi shape memory alloy films. J Mater Lett 57(20):2995–2999

    Google Scholar 

  24. Lee Z, Ophus C, Fischer LM, Fitzpatrick NN, Westra KL, Evoy S, Radmilovic V, Dahmen U, Mitlin D (2006) Metallic NEMS components fabricated from nanocomposite Al–Mo films. J Nanotechnol 17(12):3063–3070

    Google Scholar 

  25. Natarajan S, Chakraborty S, Thangavel M, Bordas S, Rabczuk T (2012) Size-dependent free flexural vibration behavior of functionally graded nanoplates. Comput Mater Sci 65:74–80

    Google Scholar 

  26. Jung WY, Han SC (2013) Analysis of sigmoid functionally graded material (S-FGM) nanoscale plates using the nonlocal elasticity theory. Math Probl Eng 49:449–458

    MathSciNet  MATH  Google Scholar 

  27. Nami MR, Janghorban M, Damadam M (2015) Thermal buckling analysis of functional graded rectangular nanoplates based on nonlocal third-order shear deformation theory. Aerosp Sci Tech 41:7–15

    Google Scholar 

  28. Hashemi SH, Bedroud M, Nazemnezhad R (2013) An exact analytical solution for free vibration of functionally graded circular/annular Mindlin nanoplates via nonlocal elasticity. Compos Struct 103:108–118

    MATH  Google Scholar 

  29. Salehipour H, Nahvi H, Shahidi AS (2015) Exact analytical solution for free vibration of functionally graded micro/nanoplates via three-dimensional nonlocal elasticity. Phys E 66:350–358

    Google Scholar 

  30. Salehipour H, Shahidi AS, Nahvi H (2015) Modified nonlocal elasticity theory for functionally graded materials. Int J Eng Sci 90:44–57

    MathSciNet  MATH  Google Scholar 

  31. Ansari R, Shojaei MF, Shahabodini A, Vahdati MB (2015) Three-dimensional bending and vibration analysis of functionally graded nanoplates by a novel differential quadrature-based approach. Compos Struct 131:753–764

    Google Scholar 

  32. Karimi M, Haddad HA, Shahidi AR (2015) Combining surface effects and non-local two variable refined plate theories on the shear/biaxial buckling and vibration of silver nanoplates. Micro Nano Lett 10(6):276–281

    Google Scholar 

  33. Karimi M, Shahidi AR (2017) Nonlocal, refined plate, and surface effects theories used to analyze free vibration of magneto-electro-elastic nanoplates under thermo-mechanical and shear loadings. Appl Phys A 123:304

    Google Scholar 

  34. Karimi M, Shahidi AR (2019) A general comparison the surface layer degree on the out-of phase and in-phase vibration behavior of a skew double-layer magneto–electro–thermo-elastic nanoplate. Appl Phys A 125:106

    Google Scholar 

  35. Karimi M, Shahidi AR (2019) Comparing magnitudes of surface energy stress in synchronous and asynchronous bending/buckling analysis of slanting double-layer METE nanoplates. Appl Phys A 125:154

    Google Scholar 

  36. Karimi M, Shahidi AR (2018) Buckling analysis of skew magneto-electro-thermo-elastic nanoplates considering surface energy layers and utilizing the Galerkin method. Appl Phys A 124:681

    Google Scholar 

  37. Farajpour MR, Shahidi AR, Farajpour A (2019) Influences of non-uniform initial stresses on vibration of small-scale sheets reinforced by shape memory alloy nanofibers. Eur Phys J Plus 134:218

    Google Scholar 

  38. Karimi M, Mirdamadi HR, Shahidi AR (2017) Positive and negative surface effects on the buckling and vibration of rectangular nanoplates under biaxial and shear in-plane loadings based on nonlocal elasticity theory. J Braz Soc Mech Sci Eng 39(4):1391–1404

    Google Scholar 

  39. Karimi M, Shokrani MH, Shahidi AR (2015) Size-dependent free vibration analysis of rectangular nanoplates with the consideration of surface effects using finite difference method. J Appl Comput Mech 1(3):122–133

    Google Scholar 

  40. Karimi M, Shahidi AR (2015) Finite difference method for sixth-order derivatives of differential equations in buckling of nanoplates due to coupled surface energy and non-local elasticity theories. Int J Nano Dimens 6(5):525–537

    Google Scholar 

  41. Karimi M, Shahidi AR (2016) Finite difference method for biaxial and uniaxial buckling of rectangular silver nanoplates resting on elastic foundations in thermal environments based on surface stress and nonlocal elasticity theories. J Solid Mech 8(4):719–733

    Google Scholar 

  42. Morteza K, Ali RS (2017) Thermo-mechanical vibration, buckling, and bending of orthotropic graphene sheets based on nonlocal two-variable refined plate theory using finite difference method considering surface energy effects. Proc IMechE Part N J Nanomater Nanoeng Nanos

  43. Farajpour MR, Shahidi AR, Farajpour A (0850a) Elastic waves in fluid-conveying carbon nanotubes under magneto-hygro-mechanical loads via a two-phase local/nonlocal mixture mode. Mater Res Express 6:0850a8

    Google Scholar 

  44. Morteza K, Ali RS (2015) A comprehensive investigation into the impact of nonlocal strain gradient and modified couple stress models on the rates of surface energy layers of BiTiO3-CoFe2O4 nanoplates: A vibration analysis. Mater Res Express

  45. Wang YZ, Li FM (2012) Static bending behaviors of nanoplate embedded in elastic matrix with small scale effects. Mech Res Comm 41:44–48

    Google Scholar 

  46. Narendar S, Gopalakrishnan S (2012) Nonlocal continuum mechanics based ultrasonic flexural wave dispersion characteristics of a monolayer graphene embedded in polymer matrix. Compos B Eng 43:3096–3103

    Google Scholar 

  47. Pouresmaeeli S, Ghavanloo E, Fazelzadeh SA (2013) Vibration analysis of viscoelastic orthotropic nanoplates resting on viscoelastic medium. Compos Struct 96:405–410

    Google Scholar 

  48. Zenkour AM, Sobhy M (2013) Nonlocal elasticity theory for thermal buckling of nanoplates lying on Winkler-Pasternak elastic substrate medium. Phys E 53:251–259

    Google Scholar 

  49. Panyatong M, Chinnaboon B, Chucheepsakul S (2015) Incorporated effects of surface stress and nonlocal elasticity on bending analysis of nanoplates embedded in an elastic medium. Suranaree J Sci Technol 22(1):21–33

    Google Scholar 

  50. Shimpi RP (2002) Refined plate theory and its variants. AIAA J 40(1):137–146

    Google Scholar 

  51. Ismail M, Hassen AA, Abdlouahed T (2010) A two variable refined plate theory for the bending analysis of functionally graded plates. Acta Mech Sin 26(6):941–949

    MathSciNet  MATH  Google Scholar 

  52. Abdelkader B, Hassaine DT, Hassen AA, Abdelouahed T, Meftah SA (2011) A four variable refined plate theory for free vibrations of functionally graded plates with arbitrary gradient. Compos B Eng 42(6):1386–1394

    Google Scholar 

  53. Thai-Huu T, Dong-Ho C (2013) Finite element formulation of various four unknown shear deformation theories for functionally graded plates. Finite Elem Anal Des 75:50–61

    MathSciNet  MATH  Google Scholar 

  54. Sobhy M (2015) A comprehensive study on FGM nanoplates embedded in an elastic medium. Compos Struct 134:966–980

    Google Scholar 

  55. Thai-Huu T, Dong-Ho C (2011) A refined plate theory for functionally graded plates resting on elastic foundation. Compos Sci Technol 71(16):1850–1858

    Google Scholar 

  56. Thai-Huu T, Park T, Dong-Ho C (2013) An efficient shear deformation theory for vibration of functionally graded plates. Arch Appl Mech 83(1):137–149

    MATH  Google Scholar 

  57. Mohammed A, Abdelouahed T, Ismail M, Abbes AEB (2011) A new trigonometric shear deformation theory for bending analysis of functionally graded plates resting on elastic foundations. KSCE J Civil Eng 15(8):1405–1414

    Google Scholar 

  58. Ramin A, Reddy JN (2009) Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J Sound Vib 326(1–2):277–289

    Google Scholar 

  59. Sobhy M (2017) A new Quasi 3D nonlocal plate theory for vibration and buckling of FGM nanoplates. IJAM 9(1):1750008

    Google Scholar 

  60. Panyatong M, Chinnaboon B, Chucheepsakul S (2016) Free vibration analysis of FG nanoplates embedded in elastic medium based on second-order shear deformation plate theory and nonlocal elasticity. Compos Struct 41(2):666–686

    Google Scholar 

Download references

Acknowledgements

This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under Grant number 107.02–2019.330.

Author information

Authors and Affiliations

  1. Faculty of Mechanical Engineering, Le Qui Don University, Hanoi, Vietnam

    Van-Ke Tran

  2. Division of Computational Mathematics and Engineering, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Quoc-Hoa Pham & Trung Nguyen-Thoi

  3. Faculty of Civil Engineering, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Quoc-Hoa Pham & Trung Nguyen-Thoi

Authors
  1. Van-Ke Tran
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Quoc-Hoa Pham
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Trung Nguyen-Thoi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Quoc-Hoa Pham.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

$$\begin{gathered} \lambdabar _{1} = \frac{1}{4}\left( {1 - \chi } \right)\left( {1 - \zeta } \right);\lambdabar _{2} = \frac{1}{4}\left( {1 + \chi } \right)\left( {1 - \zeta } \right); \hfill \\ \lambdabar _{3} = \frac{1}{4}\left( {1 + \chi } \right)\left( {1 + \zeta } \right);\lambdabar _{4} = \frac{1}{4}\left( {1 - \chi } \right)\left( {1 + \zeta } \right); \hfill \\ \hbar _{1} = \frac{1}{8}\left( {1 - \chi } \right)\left( {1 - \zeta } \right)\left( {2 - \chi - \zeta - \chi ^{2} - \zeta ^{2} } \right); \hfill \\ \hbar _{2} = \frac{1}{8}\left( {1 - \chi } \right)\left( {1 - \zeta } \right)\left( {1 - \chi ^{2} } \right)~ \hfill \\ \hbar _{3} = \frac{1}{8}\left( {1 - \chi } \right)\left( {1 - \zeta } \right)\left( {1 - \zeta ^{2} } \right) \hfill \\ \hbar _{4} = \frac{1}{8}\left( {1 + \chi } \right)\left( {1 - \zeta } \right)\left( {2 + \chi - \zeta - \chi ^{2} - \zeta ^{2} } \right); \hfill \\ \hbar _{5} = - \frac{1}{8}\left( {1 + \chi } \right)\left( {1 - \zeta } \right)\left( {1 - \chi ^{2} } \right) \hfill \\ \hbar _{6} = \frac{1}{8}\left( {1 + \chi } \right)\left( {1 - \zeta } \right)\left( {1 - \zeta ^{2} } \right) \hfill \\ \hbar _{7} = \frac{1}{8}\left( {1 + \chi } \right)\left( {1 + \zeta } \right)\left( {2 + \chi + \zeta - \chi ^{2} - \zeta ^{2} } \right); \hfill \\ \hbar _{8} = - \frac{1}{8}\left( {1 + \chi } \right)\left( {1 + \zeta } \right)\left( {1 - \chi ^{2} } \right); \hfill \\ \hbar _{9} = - \frac{1}{8}\left( {1 + \chi } \right)\left( {1 + \zeta } \right)\left( {1 - \zeta ^{2} } \right); \hfill \\ \hbar _{{10}} = \frac{1}{8}\left( {1 - \chi } \right)\left( {1 + \zeta } \right)\left( {2 - \chi + \zeta - \chi ^{2} - \zeta ^{2} } \right); \hfill \\ \hbar _{{11}} = \frac{1}{8}\left( {1 - \chi } \right)\left( {1 + \zeta } \right)\left( {1 - \chi ^{2} } \right); \hfill \\ \hbar _{{12}} = - \frac{1}{8}\left( {1 - \chi } \right)\left( {1 + \zeta } \right)\left( {1 - \zeta ^{2} } \right). \hfill \\ \end{gathered}$$

(\(\chi ;\text{\hspace{0.17em}}\zeta\): are natural coordinates)

Appendix B

$$\begin{gathered} B_{1} = \left[ {\begin{array}{*{20}l} {N_{u,x} } \\ {N_{v,y} } \\ {N_{u,y} + N_{v,x} } \\ \end{array} } \right];\;B_{2} = - \left[ {\begin{array}{*{20}l} {N_{wb,xx} } \\ {N_{wb,yy} } \\ {2N_{wb,xy} } \\ \end{array} } \right];\;B_{3} = - \left[ {\begin{array}{*{20}l} {N_{ws,xx} } \\ {N_{ws,yy} } \\ {2N_{ws,xy} } \\ \end{array} } \right];\;B_{1}^{b} = \left[ {\begin{array}{*{20}l} {N_{ws,x} } \\ {N_{ws,y} } \\ \end{array} } \right]; \hfill \\ B_{wx2} = \left[ {N_{wb,xx} + N_{ws,xx} } \right];B_{wy2} = \left[ {N_{wb,yy} + N_{ws,yy} } \right]; \hfill \\ B_{wx2} = \left[ {N_{wb,xx} + N_{ws,xx} } \right];\,B_{wy2} = \left[ {N_{wb,yy} + N_{ws,yy} } \right] \hfill \\ {\rm N} = \left[ {\begin{array}{*{20}l} {N_{u}^{T} } & {N_{v}^{T} } & {N_{wb}^{T} } & {N_{ws}^{T} } & {N_{wb,x}^{T} } & {N_{ws,x}^{T} } & {N_{wb,y}^{T} } & {N_{ws,y}^{T} } \\ \end{array} } \right]^{T} ;\,{\rm N}_{x} = \frac{\partial N}{{\partial x}};{\rm N}_{y} = \frac{\partial N}{{\partial y}} \hfill \\ D_{m} = \left[ {\begin{array}{*{20}l} {I_{0} } & 0 & 0 & 0 & {I_{1} } & {J_{1} } & 0 & 0 \\ {} & {I_{0} } & 0 & 0 & 0 & 0 & {I_{1} } & {J_{0} } \\ {} & {} & {I_{0} } & 0 & 0 & 0 & 0 & 0 \\ {} & {} & {} & {I_{0} } & 0 & 0 & 0 & 0 \\ {} & {} & {} & {} & {I_{2} } & {J_{2} } & 0 & 0 \\ {} & {} & {} & {} & {} & {K_{2} } & 0 & 0 \\ {} & {} & {} & {} & {} & {} & {I_{2} } & {J_{2} } \\ {sym} & {} & {} & {} & {} & {} & {} & {K_{2} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tran, VK., Pham, QH. & Nguyen-Thoi, T. A finite element formulation using four-unknown incorporating nonlocal theory for bending and free vibration analysis of functionally graded nanoplates resting on elastic medium foundations. Engineering with Computers 38, 1465–1490 (2022). https://doi.org/10.1007/s00366-020-01107-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01107-7

Keywords

Search

Navigation