Boundary-layer flow of the power-law fluid over a moving wedge: a linear stability analysis

Abstract

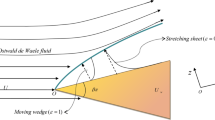
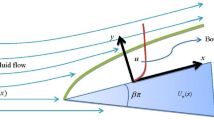
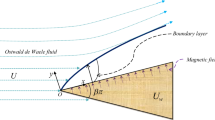
We study the stability of the two-dimensional boundary-layer flow of a power-law (Ostwald de Waele) non-Newtonian fluid over a moving wedge. The mainstream velocity is assumed to have a power of distance from the leading boundary layer, such that the system admits to the self-similar solutions. We discuss the problem in question for both shear-thickening and shear-thinning fluids which lead to a non-uniqueness (double solutions) in the base flow solutions. We then address an issue of the stability of the non-unique solutions. A linear eigenvalue analysis of the double solution reveals that the basic flow represented by the first solution is always stable, and this flow is practically encountered. The system becomes unstable to the second solutions which have the mode-two perturbations with larger boundary-layer thickness. The first and second solutions form a tongue-like structure in the solution space. Furthermore, the modification of the viscosity for the power-law fluids reveals that the system predicts an infinite viscosity in the confinement of the boundary-layer region. Extensive comparisons of the solutions with the existing models with Newtonian fluid are made, and a physical explanation behind these solutions is proposed.

Appendix

Substituting (37) in (17)–(18) and upon linearization , we have:

$$\begin{aligned} n E''(\eta ) + \frac{2}{n+1} \eta E'(\eta ) - \frac{4m}{1+(2n-1)m}E(\eta )= 0 \end{aligned}$$

(47)

with the conditions:

$$\begin{aligned} E(0) = \lambda -1,\qquad E(\infty ) = 0. \end{aligned}$$

(48)

Using the transformations:

$$\begin{aligned} E(\eta ) = {\mathcal{E}}({\hat{\eta }}),\qquad {\hat{\eta }} = \frac{\eta ^2}{n(n+1)} \end{aligned}$$

(49)

in (47), we get:

$$\begin{aligned} {\hat{\eta}}{\hat{\mathbf{E}}^{\prime\prime}}({\hat{\eta }}) + \left( \frac{1}{2} +{\hat{\eta}} \right) {\hat{\mathbf{E}}^{\prime}}({\hat{\eta }}) - \beta \left( \frac{n+1}{2}\right) {\hat{\mathbf{E}}}({\hat{\eta }}) = 0, \end{aligned}$$

(50)

which has a solution:

$$\begin{aligned}{\hat{\mathcal{E}}}({\hat{\eta }})= & e^{-{\hat{\eta }}}\left[ c_1 {\mathcal{U}}\left( \frac{1}{2} (2+(n+1)\beta );\frac{3}{2};{\hat{\eta }}\right) \nonumber \right. \\& \left. + c_2 {\mathcal{L}}\left( -\frac{1}{2} (2+(n+1)\beta );\frac{1}{2};{\hat{\eta }}\right) \right] , \end{aligned}$$

(51)

where $\beta = \frac{2m}{1+ (2n-1)m}$, ${\mathcal {U}}( \cdot , \cdot , \cdot )$, and ${\mathcal {L}}( \cdot , \cdot , \cdot )$ are the confluent hypergeometric function of second kind and Lauguerre function, respectively, and $c_1$ and $c_2$ are arbitrary constants (Abramowitz and Stegun [28] and Andrews [29]). The special functions ${\mathcal {U}}$ and ${\mathcal {L}}$ can be transformed into the confluent hypergeometric function of first kind using:

$$\begin{aligned} {\mathcal {U}}({\hat{p}},{\hat{q}},{\hat{z}})&= \frac{\pi }{\sin ({\hat{q}}\pi )}\left[ \frac{{\mathcal {M}}\left( {\hat{p}},{\hat{q}},{\hat{z}}\right) }{\Gamma \left( 1+{\hat{p}}-{\hat{q}}\right) \Gamma ({\hat{q}})} \nonumber \right. \\&\quad \left. - {{\hat{z}}}^{1-{\hat{q}}} \frac{{\mathcal {M}}\left( 1+{\hat{p}}-{\hat{q}},2-{\hat{q}},{\hat{z}}\right) }{\Gamma \left( 2-{\hat{q}}\right) \Gamma ({\hat{p}})} \right] \end{aligned}$$

(52a)

$$\begin{aligned} {\mathcal {L}}({\hat{p}},{\hat{q}},{\hat{z}})&= \frac{\Gamma \left( {\hat{p}}+{\hat{q}}+1\right) }{\Gamma (1+ {\hat{p}})~\Gamma (1+ {\hat{q}})} {\mathcal {M}}\left( -{\hat{p}},1+{\hat{q}},{\hat{z}}\right) . \end{aligned}$$

(52b)

Therefore, (51) can be written utilizing (52) in original variables (49) as:

$$\begin{aligned}&E(\eta ) =~ e^{-\frac{\eta ^2}{n(n+1)}} \frac{\eta }{\sqrt{n(n+1)}}\nonumber \\&\quad \left[ c_1~ (-\sqrt{\pi }) \left[ 2 \frac{{\mathcal {M}}\left( \frac{2+(n+1)\beta }{2};\frac{3}{2};\frac{\eta ^2}{n(n+1)}\right) }{\Gamma \left( \frac{1+(n+1)\beta }{2}\right) } \nonumber \right. \right. \\&\quad \left. \left. - \frac{\sqrt{n(n+1)}}{\eta } \frac{{\mathcal {M}}\left( \frac{1+(n+1)\beta }{2};\frac{1}{2};\frac{\eta ^2}{n(n+1)}\right) }{\Gamma \left( \frac{2+(n+1)\beta }{2}\right) }\right] \nonumber \right. \\&\quad \left. + c_2~ \frac{2}{\sqrt{\pi }}\frac{ \Gamma \left( \frac{1-(n+1)\beta }{2}\right) }{\Gamma \left( \frac{-(n+1)\beta }{2}\right) } {\mathcal {M}}\left( \frac{2+(n+1)\beta }{2};\frac{3}{2}; \frac{\eta ^2}{n(n+1)}\right) \right] . \end{aligned}$$

(53)

Using the first condition $E(0) = \lambda -1$ in (53) gives:

$$\begin{aligned} c_1 = \frac{1}{\sqrt{\pi }}\left( \lambda -1\right) ~ \Gamma \left( \frac{2+(n+1)\beta }{2}\right) . \end{aligned}$$

(54)

To eliminate $c_2$, we utilize:

$$\begin{aligned} {\mathcal {M}}({\hat{p}},{\hat{q}},{\hat{z}}) = \frac{e^{\pm i\pi {\hat{p}}} {\hat{z}}^{-{\hat{p}}}\Gamma ({\hat{q}})}{\Gamma ({\hat{q}}-{\hat{p}})} + \frac{e^{{\hat{z}}} {\hat{z}}^{{\hat{p}}-{\hat{q}}} \Gamma ({\hat{q}})}{\Gamma ({\hat{p}})} \end{aligned}$$

(55)

for ${\hat{z}}\rightarrow \infty$ in (53) gives $c_2 = 0$. Thus, the complete solution is:

$$\begin{aligned}&E(\eta ) = \frac{2(1-\lambda )}{ \sqrt{n(n+1)}} \frac{\Gamma \left( \frac{2+(1+n)\beta }{2}\right) }{\Gamma \left( \frac{1+(1+n)\beta }{2}\right) } ~\eta ~e^{-\frac{\eta ^2}{n(n+1)}}~\nonumber \\&\quad {\mathcal {M}}\left( \frac{2+(n+1)\beta }{2};\frac{3}{2};\frac{\eta ^2}{n(n+1)}\right) \nonumber \\&\quad + (\lambda -1)~e^{-\frac{\eta ^2}{n(n+1)}}~{\mathcal {M}}\left( \frac{1+(n+1)\beta }{2};\frac{1}{2};\frac{\eta ^2}{n(n+1)}\right) \end{aligned}$$

(56)

using Kummer’s transformation, we arrive at (39). Furthermore, following Abramowitz and Stegun [28], asymptotic behavior of (56) of large $\zeta$ can be approximated at leading order as:

$$\begin{aligned} E(\eta ) \approx C_1 Z^{\beta } + C_2 Z^{-(1+\beta )} Ee^{Z}+ {\mathcal {O}}|Z|^R, \end{aligned}$$

(57)

where $Z = \frac{-\zeta ^2}{2}$, and $C_1$ and $C_2$ are taken as appropriate constants. Or more precisely:

$$\begin{aligned} E(\eta ) \approx C_1 Z^{\beta } + C_2 Z^{-(1+\beta )} Ee^{Z}. \end{aligned}$$

(58)

Accordingly, the following conclusions can be drawn from (58) that:

• 1. At $m=0$: the first term behaves as constant, whereas the second term decays asymptotically to zero. Hence, the combination of both these terms tends to zero for sufficiently large $\zeta$.

• 2. For $m>0$: the first term diverges algebraically, while the second term decays to zero asymptotically. Furthermore, their linear combination becomes zero at large $\zeta$.