Appendix: Proof of block-circulant property
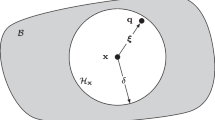
Two indices are employed to denote an individual point. The superscript represents which symmetric region the point locates, and the subscript indicates which orbit the point belongs to, as illustrated in Fig. 9 where x
i
j
, x
i+t
j
are nodal coordinates, and x
p
q
, x
p+t
q
are coordinates of integration points. x
i+t
j
and x
p+t
q
can be matched by a rotation of angle t*θ from points x
i
j
and x
p
q
, respectively. t denotes rotation order, and θ = 2π/N was defined in Sect. 2.
Based on EFG theory [1], shape function Φ
I
in Eq. 7 can be described by
$$ \Phi _{I} ={\mathbf{p}}^{\rm T} ({\mathbf{x}}){\mathbf{A}}^{{ - 1}}{\mathbf{B}}_{I} $$
(26)
where
$$ {\mathbf{p}} (x) = {\left\{ {1,x,y} \right\}}^{\rm T}, \quad {\mathbf{A}} = {\sum\limits_I {w ({\mathbf{x}} - {\mathbf{x}}_{I}){\mathbf{p}} ({\mathbf{x}}_{I}){\mathbf{p}}^{\rm T} ({\mathbf{x}}_{I}),}}\quad {\mathbf{B}}_{I} = w ({\mathbf{x}} - {\mathbf{x}}_{I}){\mathbf{p}} ({\mathbf{x}}_{I}) $$
(27)
$$ w ({\mathbf{x}}^{p}_{q} - {\mathbf{x}}^{i}_{j}) = w ({\mathbf{x}}^{{p + t}}_{q} - {\mathbf{x}}^{{i + t}}_{j}) $$
(28)
In a symmetric system, points belonging to the same orbit (see Fig. 9) follow
$$ {\mathbf{x}}^{{i + t}}_{j} ={\mathbf{T}}_{t} \cdot{\mathbf{x}}^{i}_{j},\quad {\mathbf{T}}_{t} =\left[ \begin{array}{*{20}c} {{\cos t\theta}}&{{ - \sin t\theta}}\\ {{\sin t\theta}}&{{\cos t\theta}} \end{array} \right] $$
(29)
and
$$ {\mathbf{T}}_{{i + k - 1}} ={\mathbf{T}}_{i} \cdot{\mathbf{T}}_{k} $$
(30)
Substituting Eq. 29 for 27 then yields
$${\mathbf{p}} ({\mathbf{x}}^{{i + t}}_{j}) = \overline{{\mathbf{\alpha}}} \cdot{\mathbf{p}} ({\mathbf{x}}^{i}_{j}),\quad {\mathbf{p}} ({\mathbf{x}}^{{p + t}}_{q}) = \overline{{\mathbf{\alpha}}} \cdot{\mathbf{p}} ({\mathbf{x}}^{p}_{q}),\quad \overline{{\mathbf{\alpha}}} =\left[{\begin{array}{*{20}c} {1}&{0} \\ {0}&{{{\mathbf{T}}_{t}}} \end{array}}\right] $$
(31)
Utilizing Eqs. 26–29 and 31, one can obtain
$$\Phi ^{i}_{j} ({\mathbf{x}}^{p}_{q}) ={\mathbf{p}}^{\rm T} ({\mathbf{x}}^{p}_{q}){\mathbf{A}}^{{ - 1}}{\mathbf{B}}^{i}_{j} $$
(32)
$$ \begin{aligned} \Phi ^{{i + t}}_{j} ({\mathbf{x}}^{{p + t}}_{q}) &={\mathbf{p}}^{\rm T} ({\mathbf{x}}^{{p + t}}_{q}){\mathbf{A}}^{{ - 1}}{\mathbf{B}}^{{i + t}}_{j} \\ &={\mathbf{p}}^{\rm T} ({\mathbf{x}}^{{p + t}}_{q})\left[{\sum\limits_i{{\sum\limits_j{w ({\mathbf{x}}^{{p + t}}_{q} -{\mathbf{x}}^{{i + t}}_{j}){\mathbf{p}} ({\mathbf{x}}^{{i + t}}_{j}){\mathbf{p}}^{\rm T} ({\mathbf{x}}^{{i + t}}_{j})}}}}\right]^{{ - 1}} w ({\mathbf{x}}^{{p + t}}_{q} -{\mathbf{x}}^{{i + t}}_{j}){\mathbf{p}} ({\mathbf{x}}^{{i + t}}_{j}) \\ &={\mathbf{p}}^{\rm T} ({\mathbf{x}}^{p}_{q})\overline{{\mathbf{\alpha}}} ^{\rm T} \left[{\sum\limits_i{{\sum\limits_j{w ({\mathbf{x}}^{p}_{q} -{\mathbf{x}}^{i}_{j})\overline{{\mathbf{\alpha}}}{\mathbf{p}} ({\mathbf{ x}}^{i}_{j}){\mathbf{p}}^{\rm T} ({\mathbf{x}}^{i}_{j})}}}}\overline{{\mathbf {\alpha}}} ^{\rm T} \right]^{{ - 1}} w ({\mathbf{x}}^{p}_{q} -{\mathbf{x}}^{i}_{j})\overline{{\mathbf{\alpha}}}{\mathbf{p}} ({\mathbf{ x}}^{i}_{j}) \\ &={\mathbf{p}}^{\rm T} ({\mathbf{x}}^{p}_{q})\overline{{\mathbf{\alpha}}} ^{\rm T} (\overline{{\mathbf{\alpha}}} ^{\rm T})^{{ - 1}} \left[{\sum\limits_i{{\sum\limits_j{w ({\mathbf{x}}^{p}_{q} -{\mathbf{x}}^{i}_{j}){\mathbf{p}} ({\mathbf{x}}^{i}_{j}){\mathbf{p}}^{\rm T} ({\mathbf{x}}^{i}_{j})}}}}\right]^{{ - 1}} \overline{{\mathbf{\alpha}}} ^{{ - 1}} \overline{{\mathbf{\alpha}}} w ({\mathbf{x}}^{p}_{q} -{\mathbf{x}}^{i}_{j}){\mathbf{p}} ({\mathbf{x}}^{i}_{j}) \\ &={\mathbf{p}}^{\rm T} ({\mathbf{x}}^{p}_{q})\left[{\sum\limits_i{{\sum\limits_j{w ( {\mathbf{x}}^{p}_{q} -{\mathbf{x}}^{i}_{j}){\mathbf{p}} ({\mathbf{x}}^{i}_{j}){\mathbf{p}}^{\rm T} ({\mathbf{x}}^{i}_{j})}}}}\right]^{{ - 1}} w ({\mathbf{x}}^{p}_{q} -{\mathbf{x}}^{i}_{j}){\mathbf{p}} ({\mathbf{x}}^{i}_{j}) \\ &={\mathbf{p}}^{\rm T} ({\mathbf{x}}^{p}_{q}){\mathbf{A}}^{{ - 1}}{\mathbf{B}}^{i}_{j} \\ \end{aligned} $$
(33)
therefore
$$ \Phi ^{i}_{j} (x^{p}_{q}) = \Phi ^{{i + t}}_{j} (x^{{p + t}}_{q}) $$
(34)
$$ \frac{\partial}{{\partial x^{i}}}\Phi ^{i}_{j} \left|{_{{x^{t}_{q}}}} \right. = \frac{\partial}{{\partial x^{{i + t}}}}\left.{\Phi ^{{i + t}}_{j}} \right|_{{{\mathbf{x}}^{{p + t}}_{q}}} = \left(\cos (t\theta)\frac{{\partial}}{{\partial x^{i}}} + \sin (t\theta)\frac{\partial}{{\partial y^{i}}}\right)\left.{\Phi ^{{i + t}}_{j}} \right|_{{{\mathbf{x}}^{{p + t}}_{q}}} $$
(35)
$$ \frac{\partial}{{\partial y^{i}}}\Phi ^{i}_{j} \left|{_{{x^{p}_{q}}}} \right. = \frac{\partial}{{\partial y^{{i + t}}}}\left.{\Phi ^{{i + t}}_{j}} \right|_{{{\mathbf{x}}^{{p + t}}_{q}}} = \left( - \sin (t\theta)\frac{\partial}{{\partial x^{i}}} + \cos (t\theta)\frac{\partial}{{\partial y^{i}}}\right)\left.{\Phi ^{{i + t}}_{j}} \right|_{{{\mathbf{x}}^{{p + t}}_{q}}} $$
(36)
$$ \frac{\partial}{{\partial x^{i}}}\left.{\Phi ^{{i + t}}_{j}} \right|_{{{\mathbf{x}}^{{p + t}}_{q}}} = \left(\cos (t\theta)\frac{\partial}{{\partial x^{i}}} - \sin (t\theta)\frac{\partial}{{\partial y^{i}}}\right)\left.{\Phi ^{i}_{j}} \right|_{{{\mathbf{x}}^{p}_{q}}} $$
(37)
$$ \frac{\partial}{{\partial y^{i}}}\left.{\Phi ^{{i + t}}_{j}} \right|_{{{\mathbf{x}}^{{p + t}}_{q}}} = \left(\sin (t\theta)\frac{\partial}{{\partial x^{i}}} + \cos (t\theta)\frac{\partial}{{\partial y^{i}}}\right)\left.{\Phi ^{i}_{j}} \right|_{{{\mathbf{x}}^{p}_{q}}} $$
(38)
Based on Eqs. 37, 38, one can obtain
$$ \left.({\mathbf{L}}^{\rm T} \Phi ^{i}_{j}){\mathbf{D}} ({\mathbf{L}}\Phi ^{k}_{l})\right|_{{{\mathbf{x}}^{p}_{q}}} =\left[ \begin{array}{*{20}c} {{xi}}&{0}&{{yi}} \\ {0}&{{yi}}&{{xi}} \end{array} \right] \cdot{\mathbf{D}} \left[{ \begin{array}{*{20}c} {{xk}}&{0} \\ {0}&{{xk}}\\ {{yk}}&{{xk}} \end{array}} \right] $$
(39)
$$ \begin{aligned} \left.{\mathbf{\alpha}}^{\rm T} ({\mathbf{L}}^{\rm T} \Phi ^{{i + t}}_{j}){\mathbf{D}} ({\mathbf{L}}\Phi ^{{k + t}}_{l}){\mathbf{\alpha}}\right|_{{{\mathbf{x}}^{{p + 1}}_{q}}} & =\left[ \begin{array}{*{20}c} {{\cos (t\theta)}}&{{\sin (t\theta)}} \\ {{- \sin (t\theta)}}&{{\cos (t\theta)}} \end{array}\right] \\ & \quad \times \left[ \begin{array}{*{20}c} {{\cos (t\theta) \cdot xi -\sin (t\theta) \cdot yi}}&{0}&{{\sin (t\theta) \cdot xi + \cos (t\theta) \cdot yi}} \\ {0}&{{\sin (t\theta) \cdot xi + \cos (t\theta) \cdot yi}}&{{\cos (t\theta) \cdot xi - \sin (t\theta) \cdot yi}} \end{array}\right] \\ & \quad \times{\mathbf{D}} \left[ \begin{array}{*{20}c} {{\cos (t\theta) \cdot xk -\sin (t\theta) \cdot yk}}&{0} \\ {0}&{{\sin (t\theta) \cdot xk +\cos (t\theta) \cdot yk}} \\ {{\sin (t\theta) \cdot xk + \cos (t\theta)\cdot yk}}&{{\cos (t\theta) \cdot xk - \sin (t\theta) \cdot yk}} \end{array} \right] \left[ \begin{array}{*{20}c} {{\cos (t\theta)}}&{{- \sin (t\theta)}} \\ {{\sin (t\theta)}}&{{\cos (t\theta)}} \end{array} \right] \\ \end{aligned} $$
(40)
where
$$ xi = \frac{\partial}{{\partial x^{i}}}\left.{\Phi ^{i}_{j}} \right|_{{{\mathbf{x}}^{p}_{q}}} ,\quad yi = \frac{\partial}{{\partial y^{i}}}\left.{\Phi ^{i}_{j}} \right|_{{{\mathbf{x}}^{p}_{q}},}\quad{\mathbf{\alpha}} ={\mathbf{T}}_{t} $$
(41)
Comparing Eq. 39 with Eq. 40 in details then gives
$$ \left.{ ({\mathbf{L}}^{\rm T} \Phi ^{i}_{j}){\mathbf{D}} ({\mathbf{L}}\Phi ^{k}_{l})} \right|_{{{\mathbf{x}}^{p}_{q}}} = \left.{{\mathbf{\alpha}}^{\rm T} ({\mathbf{L}}^{\rm T} \Phi ^{{i + t}}_{j}){\mathbf{D}} ({\mathbf{L}}\Phi ^{{k + t}}_{l}){\mathbf{\alpha}}} \right|_{{{\mathbf{x}}^{{p + t}}_{q}}} $$
(42)
therefore
$$ {\mathbf{T}}^{\rm T}_{p} \cdot{\mathbf{K}}^{{pk}}_{{ql}} \cdot{\mathbf{T}}_{k} ={\mathbf{T}}^{\rm T}_{{p + t}} \cdot{\mathbf{K}}^{{p + t,k + t}}_{{ql}} \cdot{\mathbf{T}}_{{k + t}} $$
(43)
$$ \overline{{\mathbf{T}}} ^{\rm T}_{p} \cdot{\mathbf{K}}^{{pk}} \cdot \overline{{\mathbf{T}}} _{k} = \overline{{\mathbf{T}}} ^{\rm T}_{{p + t}} \cdot{\mathbf{K}}^{{p + t,k + t}} \cdot \overline{{\mathbf{T}}} _{{k + t}} $$
(44)
$$ \overline{{\mathbf{K}}} ^{{ik}} = \overline{{\mathbf{K}}} ^{{i +t,k + t}} $$
(45)
Similarly, it can be proved that
$$ \overline{{\mathbf{G}}} ^{{ik}} = \overline{{\mathbf{G}}} ^{{i + t,k + t}} $$
(46)