Impact of releasing period and magnitude on mosquito population in a sterile release model with delay

Abstract

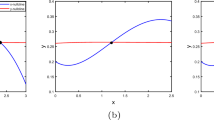
Assuming that there are multiple batches of sterile males reared and released during the maturation period, we derive a switching delay differential model to study the fate of wild females under an impulsive and periodic release of sterile males. For the release magnitude of each batch c, we find two threshold values $c_1^*$ and $c_2^*$, and prove that when $c\in (0, c_1^*]$, the model admits exactly two periodic solutions, among which one is asymptotically stable and the other is unstable. The trivial equilibrium, corresponding to the elimination of wild females, is locally asymptotically stable, and it becomes globally asymptotically stable when $c\ge c_2^*$. One key step is to prove that every solution is sandwiched between two “good” solutions.

Appendices

Appendices

Model derivation satisfying (1.5) and (1.6)

For the release strategy with (1.5) and (1.6), sterile males released at $t_i=iT$, $i=0, 1, \cdots$ can keep sexually competitive until $iT+\overline{{T}}=(i+p)T+q$. Then for $t\in [0, pT)$, we have

$$\begin{aligned} g(t)=ic, \ t\in [(i-1)T, iT), \ i=1, 2, \ldots , p. \end{aligned}$$

(A.1)

From the $p+1$-cycle, g(t) is a T-periodic function defined as

$$\begin{aligned} g(t)= pc, \ t\ge pT, \ \text {if}\ q=0, \end{aligned}$$

(A.2)

and

$$\begin{aligned} g(t) = {\left\{ \begin{array}{ll} (p + 1)c, &{} t \in [iT, iT + q),\\ p c, &{} t \in [iT + q, (i+1)T), \end{array}\right. }\quad \text{ if }\ \ q\ne 0, \end{aligned}$$

(A.3)

for $i=p, p+1, \ldots$. (See Fig. 6 for illustration of g(t) when $q\ne 0$.)

Fig. 6

Schematic graph of the release function g(t) with $\overline{{T}}=pT+q$ satisfying $q\ne 0$

It is obvious that $g(t-\tau )\equiv 0$ for $t\in [0, \tau )$. To determine $g(t-\tau )$ for $t\ge \tau$, we need to locate $\tau$ relative to T and $\overline{{T}}$. With $\overline{{T}}\le \tau =mT$, we have three cases to consider when specifying $g(t-\tau )$ as well as the corresponding model (1.2).

1.1 Model (1.2) with $q=0$ and $m=p$

In this case, from (A.1) and (A.2), we have

$$\begin{aligned} g(t) = {\left\{ \begin{array}{ll} ic, &{} t \in [ (i-1)T, iT),\ i=1, 2, \ldots , p-1, \\ pc, &{} t\in [(p-1)T, \infty ). \end{array}\right. } \end{aligned}$$

(A.4)

Hence

$$\begin{aligned} g(t-\tau ) = {\left\{ \begin{array}{ll} 0, &{} t \in [0, pT),\\ ic, &{} t \in [(p+ i-1)T, (p+i)T),\ i=1, 2, \ldots , p-1, \\ pc, &{} t\in [(2p-1)T, \infty ). \end{array}\right. } \end{aligned}$$

(A.5)

During the first p cycles, $g(t-\tau )\equiv 0$ and the wild mosquito population follows

$$\begin{aligned} \dfrac{dw}{dt}=a w(t-\tau ) - \left[ \mu + \xi (w(t)+ic)\right] w(t),\ t\in [ (i-1)T, iT), \ i=1, 2, \ldots , p, \end{aligned}$$

where $a=a_0e^{-\mu _0\tau }$.

The first time point with $g(t-\tau )\ne 0$ is $t=pT$, and these sterile mosquitoes accumulate to $(p-1)c$ at $t=2(p-1)T$. Therefore, when $t \in [(p+ i-1)T, (p+i)T)$, we get

$$\begin{aligned} \dfrac{dw}{dt}=\dfrac{a w^2(t-\tau )}{w(t-\tau )+ic} - \left[ \mu + \xi (w(t)+pc)\right] w(t), \ i=1, 2, \ldots , p-1. \end{aligned}$$

From $t=(2p-1)T$ and thereafter, $g(t-\tau )=g(t)\equiv pc$. Eventually, the dynamics of the wild mosquitoes then obey

$$\begin{aligned} \dfrac{dw}{dt}= \dfrac{a w^2(t-\tau )}{w(t-\tau )+pc} - \left[ \mu + \xi (w(t)+pc)\right] w(t), \ t\ge (2p-1)T. \end{aligned}$$

(A.6)

1.2 Model (1.2) with $q=0$ and $m>p$

In this case, we have

$$\begin{aligned} g(t-\tau ) = {\left\{ \begin{array}{ll} 0, &{} t \in [0, mT),\\ ic, &{} t \in [(m + i-1)T, (m+i)T),\ i=1, 2, \cdots , p-1, \\ pc, &{} t\in [(m+p-1)T, \infty ). \end{array}\right. } \end{aligned}$$

(A.7)

Together with (A.4), the model (1.2) becomes

$$\begin{aligned} \left\{ \begin{aligned} \dfrac{dw}{dt}=&a w(t-\tau ) - \left[ \mu + \xi (w(t)+ic)\right] , t\in [ (i-1)T, iT), \ i=1, 2, \ldots , p-1, \\ \dfrac{dw}{dt}=&a w(t-\tau ) - \left[ \mu + \xi (w(t)+pc)\right] , t\in [(i-1)T, iT), \ i=p, p+1, \ldots , m, \\ \dfrac{dw}{dt}=&\dfrac{a w^2(t-\tau )}{w(t-\tau )+ic} - \left[ \mu + \xi (w(t)+pc)\right] w(t), \\&\qquad \qquad t \in [(i+m-1)T, (i+m)T), i=1, 2, \ldots , p-1,\\ \dfrac{dw}{dt}=&\dfrac{a w^2(t-\tau )}{w(t-\tau )+pc} - \left[ \mu + \xi (w(t)+pc)\right] w(t), \ t\ge (m+p-1)T. \end{aligned} \right. \end{aligned}$$

The dynamics of the wild mosquitoes eventually follow

$$\begin{aligned} \dfrac{dw}{dt}= \dfrac{a w^2(t-\tau )}{w(t-\tau )+pc} - \left[ \mu + \xi (w(t)+pc)\right] w(t), \ t\ge (m+p-1)T, \end{aligned}$$

(A.8)

by ignoring the first $m+p-1$ cycles.

1.3 Model (1.2) with $q\ne 0$ and $m>p$

From (A.1) and (A.3), we have

$$\begin{aligned} g(t-\tau ) ={\left\{ \begin{array}{ll} 0, &{} \ t \in [0, mT), \\ ic, &{} \ t \in [(i+m-1)T, (i+m)T),\ i=1, 2, \ldots , p, \\ (p+1)c, &{} \ t\in [(i+m)T, (i+m)T+q), \ i=p, p+1, \ldots , \\ pc, &{} \ t\in [ (i+m)T+q, (i+m+1)T),\ i=p, p+1, \ldots . \end{array}\right. } \end{aligned}$$

(A.9)

Since

$$\begin{aligned}{}[0, mT)=[0, pT)\cup \big (\cup _{k=p}^{m-1} [kT,kT+q)\cup [kT+q, (k+1)T)\big ), \end{aligned}$$

when $t\in [0, mT)$, model (1.2) obeys the following three equations:

$$\begin{aligned} \left\{ \begin{aligned} \dfrac{dw}{dt}=&a w(t-\tau ) - \left[ \mu + \xi (w(t)+ic)\right] , t\in [(i-1)T, iT), \ i=1, 2, \ldots , p, \\ \dfrac{dw}{dt}=&a w(t-\tau ) - \left[ \mu + \xi (w(t)+(p+1)c)\right] , t\in [iT, iT+q), \ i=p, p+1, \ldots , m-1, \\ \dfrac{dw}{dt}=&a w(t-\tau ) - \left[ \mu + \xi (w(t)+pc)\right] w(t), t \in [iT+q, (i+1)T), \ i=p, p+1, \ldots , m-1. \end{aligned} \right. \end{aligned}$$

From $t=mT$, the function $g(t-\tau )\ne 0$. For $t\in [mT, (m+p)T)$, from (A.3) and (A.9), model (1.2) switches between

$$\begin{aligned} \dfrac{dw}{dt}= \dfrac{a w^2(t-\tau )}{w(t-\tau )+ic} - \left[ \mu + \xi (w(t)+(p+1)c)\right] w(t), \ t\in [iT, iT+q), \end{aligned}$$

and

$$\begin{aligned} \dfrac{dw}{dt}=\dfrac{a w^2(t-\tau )}{w(t-\tau )+ic} - \left[ \mu + \xi (w(t)+pc)\right] w(t), \ t\in [iT+q, (i+1)T), \end{aligned}$$

where $i=m, m+1, \cdots , m+p-1$.

After running the first $m+p$ cycles, (A.3) and (A.9) imply that model (1.2) follows the switching system consisting of two delay differential equations

$$\begin{aligned} \left\{ \begin{aligned} \dfrac{dw}{dt}=&\dfrac{a w^2(t-\tau )}{w(t-\tau )+(p+1)c} - \left[ \mu + \xi (w(t)+(p+1)c)\right] w(t), \ t\in [iT, iT+q), \\ \dfrac{dw}{dt}=&\dfrac{a w^2(t-\tau )}{w(t-\tau )+pc} - \left[ \mu + \xi (w(t)+pc)\right] w(t), \ t\in [ iT+q, (i+1)T), \ \end{aligned} \right. \end{aligned}$$

for $i=p+m, p+m+1, \cdots$.