Optimal control of vaccination in a vector-borne reaction–diffusion model applied to Zika virus

Abstract

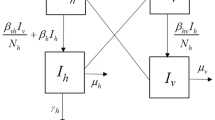
Zika virus has acquired worldwide concern after a recent outbreak in Latin America that started in Brazil, with associated neurological conditions such as microcephaly in newborns from infected mothers. The virus is transmitted mainly by Aedes aegypti mosquitoes, but direct (sexual) transmission has been documented. We formulate a reaction diffusion model that considers spatial movement of humans and vectors, with local contact transmission of Zika virus. Vaccination is introduced as a control variable, giving immunity to susceptible humans, in order to characterize an optimal vaccination strategy that minimizes the costs associated with infections and vaccines. The optimal control characterization is obtained in terms of state and adjoint equations. Parameter estimation and numerical simulations are carried out using data for the initial 2015 Zika outbreak in the state of Rio Grande do Norte in Brazil. Several scenarios are considered and analyzed in terms of number of new infections and costs, showing that the optimal control application is successful, significantly reducing these quantities.

Appendix: Derivation of optimal control

We seek to find an optimal control $u^* \in U$ satisfying (4), where U is the set of admissible controls defined in (3). This optimization problem is subject to the state system (1), with state functions in $L^2(0,T;H^1(\varOmega ))$ and corresponding time derivatives in $L^2(0,T;H^1(\varOmega )^*)$. In order to find $u^*$, we have to solve an optimality system, which consists of the state PDEs, adjoint PDEs, and the optimal control characterization. To obtain the sensitivity system, we must differentiate the control-to-state map $u \rightarrow \left( S,I,R,S_v,I_v \right) (u)$. We use that system and the objective functional to find the adjoint system. Then we use the sensitivity and adjoint system to simplify the derivative of the map $u \rightarrow J(u)$, finally obtaining the desired optimal control characterization. The derivatives of both of these maps are computed as Fréchet derivatives (derivatives in dircetion $\ell$). In the following, we provide an overview of the derivation of the sensitivity and adjoint equations, and the control characterization. Details about optimal control theory in PDEs can be found in De Silva et al. (2017), Fister (1997), Lenhart and Workman (2007), Li and Yong (2012), Lions (1971).

1.1 Sensitivity system

From the control-to-state map, we define $(S^\epsilon ,I^\epsilon ,R^\epsilon ,S_v^\epsilon ,I_v^\epsilon ) = (S,I,R,S_v,I_v)(u + \epsilon \ell )$. We then define the sensitivity functions, which are Gateaux derivatives of the control-to-state map:

$$\begin{aligned}&\dfrac{S^\epsilon - S}{\epsilon } \rightharpoonup \psi _1, \ \dfrac{I^\epsilon - I}{\epsilon } \rightharpoonup \psi _2, \ \dfrac{R^\epsilon - R}{\epsilon } \rightharpoonup \psi _3, \ \dfrac{S_v^\epsilon - S_v}{\epsilon } \rightharpoonup \psi _4, \\&\quad \dfrac{I_v^\epsilon - I_v}{\epsilon } \rightharpoonup \psi _5, \text { as } \epsilon \rightarrow 0. \end{aligned}$$

We also have:

$$\begin{aligned} S^\epsilon \rightarrow S, \ I^\epsilon \rightarrow I, \ R^\epsilon \rightarrow R, \ S_v^\epsilon \rightarrow S_v, \ I_v^\epsilon \rightarrow I_v, \text { as } \epsilon \rightarrow 0. \end{aligned}$$

(13)

The sensitivity functions $\varvec{\psi }=(\psi _1,\psi _2,\psi _3,\psi _4,\psi _5)$ satisfy a system corresponding to a linearized version of the state equations. See works by De Silva et al. (2017), Li and Yong (2012), and Lions (1971) to show justification of such convergence of these quotients and the existence of the sensitivity functions and their PDEs. These equations are used to derive PDEs for the adjoint $\varvec{\lambda }=(\lambda _1,\lambda _2,\lambda _3,\lambda _4,\lambda _5)$, where each adjoint variable is associated with a state variable.

We now calculate equations for the sensitivity functions. We calculate an equation for the quotient $\dfrac{S^\epsilon - S}{\epsilon }$:

$$\begin{aligned} \begin{aligned}&\left( \dfrac{S^\epsilon - S}{\epsilon } \right) _t - \dfrac{\nabla \cdot \left( \alpha \nabla S^\epsilon \right) - \nabla \cdot \left( \alpha \nabla S \right) }{\epsilon } = - \beta \left( \dfrac{ S^\epsilon I_v^\epsilon - S^\epsilon I_v + S^\epsilon I_v - S I_v}{\epsilon } \right) \\&\quad - \beta _d \left( \dfrac{ S^\epsilon I^\epsilon - S^\epsilon I + S^\epsilon I - S I}{\epsilon } \right) - u \left( \dfrac{S^\epsilon - S}{\epsilon }\right) - \ell S^\epsilon . \end{aligned} \end{aligned}$$

Letting $\epsilon \rightarrow 0$, passing to the limit gives:

$$\begin{aligned} \begin{aligned} (\psi _1)_t - \nabla \cdot \left( \alpha \psi _1 \right) + \beta \left( S \psi _5 + \psi _1 I_v \right) + \beta _d \left( S \psi _2 + \psi _1 I \right) + u \psi _1 = - \ell S. \end{aligned} \end{aligned}$$

In the same way, letting $\epsilon \rightarrow 0$ in

$$\begin{aligned} \begin{aligned}&\left( \dfrac{I^\epsilon - I}{\epsilon } \right) _t - \dfrac{\nabla \cdot \left( \alpha _I \nabla I^\epsilon \right) - \nabla \cdot \left( \alpha \nabla I \right) }{\epsilon } = \beta \left( \dfrac{ S^\epsilon I_v^\epsilon - S^\epsilon I_v + S^\epsilon I_v - S I_v}{\epsilon } \right) \\&\quad +\beta _d \left( \dfrac{ S^\epsilon I^\epsilon - S^\epsilon I + S^\epsilon I - S I}{\epsilon } \right) - \delta \left( \dfrac{I^\epsilon - I}{\epsilon }\right) + \left( \dfrac{f - f}{\epsilon } \right) \end{aligned} \end{aligned}$$

gives:

$$\begin{aligned} \begin{aligned} (\psi _2)_t - \nabla \cdot \left( \alpha _I \psi _2 \right) - \beta \left( S \psi _5 + \psi _1 I_v \right) - \beta _d \left( S \psi _2 + \psi _1 I \right) + \delta \psi _2 = 0. \end{aligned} \end{aligned}$$

Note that the term with external source f vanishes because it depends only on (x, t). Similarly:

$$\begin{aligned} \begin{aligned}&\left( \dfrac{R^\epsilon - R}{\epsilon } \right) _t - \dfrac{\nabla \cdot \left( \alpha \nabla R^\epsilon \right) - \nabla \cdot \left( \alpha \nabla R \right) }{\epsilon } = u \left( \dfrac{S^\epsilon - S}{\epsilon }\right) + \ell S^\epsilon + \delta \left( \dfrac{I^\epsilon - I}{\epsilon } \right) , \end{aligned} \end{aligned}$$

gives:

$$\begin{aligned} \begin{aligned} (\psi _3)_t - \nabla \cdot \left( \alpha \psi _3 \right) - u \psi _1 - \delta \psi _2 = \ell S. \end{aligned} \end{aligned}$$

For $S_v$, we obtain:

$$\begin{aligned} \begin{aligned}&\left( \dfrac{S_v^\epsilon - S_v}{\epsilon } \right) _t - \dfrac{\nabla \cdot \left( \alpha _v \nabla S_v^\epsilon \right) - \nabla \cdot \left( \alpha _v \nabla S_v \right) }{\epsilon } = - \beta _v \left( \dfrac{ S_v^\epsilon I^\epsilon - S_v^\epsilon I + S_v^\epsilon I - S_v I}{\epsilon } \right) \\&\quad + r_v \left( \dfrac{S_v^\epsilon - S_v}{\epsilon }\right) + r_v \left( \dfrac{I_v^\epsilon - I_v}{\epsilon }\right) - \dfrac{r_v}{\kappa _v} \left( \dfrac{ S_v^\epsilon S_v^\epsilon - S_v^\epsilon S_v + S_v^\epsilon S_v - S_v S_v}{\epsilon } \right) \\&\quad - \dfrac{2 r_v}{\kappa _v} \left( \dfrac{ S_v^\epsilon I_v^\epsilon - S_v^\epsilon I_v + S_v^\epsilon I_v - S_v I_v}{\epsilon } \right) - \dfrac{r_v}{\kappa _v} \left( \dfrac{ I_v^\epsilon I_v^\epsilon - I_v^\epsilon I_v + I_v^\epsilon I_v - I_v I_v}{\epsilon } \right) , \end{aligned} \end{aligned}$$

and:

$$\begin{aligned} \begin{aligned}&(\psi _4)_t - \nabla \cdot \left( \alpha _v \psi _4 \right) + \beta _v \left( S_v \psi _2 + \psi _4 I \right) - r_v \left( \psi _4 + \psi _5 \right) \\&\qquad + \dfrac{2 r_v}{\kappa _v} \left( S_v + I_v \right) \left( \psi _4 + \psi _5 \right) = 0. \end{aligned} \end{aligned}$$

Similarly, for $I_v$ we have:

$$\begin{aligned} \begin{aligned}&\left( \dfrac{I_v^\epsilon - I_v}{\epsilon } \right) _t - \dfrac{\nabla \cdot \left( \alpha _v \nabla I_v^\epsilon \right) - \nabla \cdot \left( \alpha _v \nabla I_v \right) }{\epsilon }\\&\quad = + \beta _v \left( \dfrac{ S_v^\epsilon I^\epsilon - S_v^\epsilon I + S_v^\epsilon I - S_v I}{\epsilon } \right) - \mu _v \left( \dfrac{S_v^\epsilon - S_v}{\epsilon }\right) , \end{aligned} \end{aligned}$$

and:

$$\begin{aligned} \begin{aligned} (\psi _5)_t - \nabla \cdot \left( \alpha _v \psi _5 \right) - \beta _v \left( S_v \psi _2 + \psi _4 I \right) + \mu _v \psi _5 = 0. \end{aligned} \end{aligned}$$

In a similar way, we obtain initial conditions:

$$\begin{aligned} \psi _1(\varvec{x},0) = \psi _2(\varvec{x},0) = \psi _3(\varvec{x},0) = \psi _4(\varvec{x},0) = \psi _5(\varvec{x},0) = 0, \ \text {in} \ \varOmega , \end{aligned}$$

and boundary conditions:

$$\begin{aligned} \dfrac{\partial \psi _1}{\partial \varvec{n}} = \dfrac{\partial \psi _2}{\partial \varvec{n}} = \dfrac{\partial \psi _3}{\partial \varvec{n}} = \dfrac{\partial \psi _4}{\partial \varvec{n}} = \dfrac{\partial \psi _5}{\partial \varvec{n}} = 0 \ \text {in} \ \partial \varOmega \times (0,T). \end{aligned}$$

We can write the sensitivity system in vector form as following:

$$\begin{aligned} \mathscr {L} \begin{pmatrix} \psi _1 \\ \psi _2 \\ \psi _3 \\ \psi _4 \\ \psi _5 \\ \end{pmatrix} = \begin{pmatrix} -\ell S \\ 0 \\ \ell S \\ 0 \\ 0 \\ \end{pmatrix}, \end{aligned}$$

where:

$$\begin{aligned} \mathscr {L} \begin{pmatrix} \psi _1 \\ \psi _2 \\ \psi _3 \\ \psi _4 \\ \psi _5 \\ \end{pmatrix} = \begin{pmatrix} (\psi _1)_t - \nabla \cdot (\alpha \nabla \psi _1) \\ (\psi _2)_t - \nabla \cdot (\alpha _I \nabla \psi _2) \\ (\psi _3)_t - \nabla \cdot (\alpha \nabla \psi _3) \\ (\psi _4)_t - \nabla \cdot (\alpha _v \nabla \psi _4) \\ (\psi _5)_t - \nabla \cdot (\alpha _v \nabla \psi _5) \\ \end{pmatrix} + \varvec{M} \begin{pmatrix} \psi _1 \\ \psi _2 \\ \psi _3 \\ \psi _4 \\ \psi _5 \\ \end{pmatrix}, \end{aligned}$$

and the matrix $\varvec{M}^T$ is given by (6).

1.2 Adjoint system

For the adjoint variables $\varvec{\lambda }=(\lambda _1,\ldots , \lambda _5)$, the adjoint operator is obtained from the relation:

$$\begin{aligned} \langle \varvec{\lambda } , \mathscr {L} \varvec{\psi } \rangle = \langle \mathscr {L}^* \varvec{\lambda } , \varvec{\psi } \rangle \end{aligned}$$

(14)

in the appropriate weak $L^2(Q)$ sense. The right hand side of the adjoint system is given by the derivatives of the integrand of the objective functional, with respect to the states:

$$\begin{aligned} \begin{aligned} \dfrac{\partial }{\partial S} \left( c_1 I + c_2 u S + c_3 u^2 \right)&= c_2 u, \\ \dfrac{\partial }{\partial I} \left( c_1 I + c_2 u S + c_3 u^2 \right)&= c_1, \\ \dfrac{\partial }{\partial R} \left( c_1 I + c_2 u S + c_3 u^2 \right)&= 0, \\ \dfrac{\partial }{\partial S_v} \left( c_1 I + c_2 u S + c_3 u^2 \right)&= 0, \\ \dfrac{\partial }{\partial I_v} \left( c_1 I + c_2 u S + c_3 u^2 \right)&= 0. \end{aligned} \end{aligned}$$

We use the expression (14) in order to derive the operators in the adjoint system. This is done using integration by parts on $\langle \varvec{\lambda } , \mathscr {L} \varvec{\psi } \rangle$ and the boundary conditions of the sensitivity equations. The adjoint system obtained this way is:

$$\begin{aligned} \mathscr {L^*} \begin{pmatrix} \lambda _1 \\ \lambda _2 \\ \lambda _3 \\ \lambda _4 \\ \lambda _5 \\ \end{pmatrix} = \begin{pmatrix} c_2 u \\ c_1 \\ 0 \\ 0 \\ 0 \\ \end{pmatrix}, \end{aligned}$$

where:

$$\begin{aligned} \mathscr {L}^* \begin{pmatrix} \lambda _1 \\ \lambda _2 \\ \lambda _3 \\ \lambda _4 \\ \lambda _5 \\ \end{pmatrix} = \begin{pmatrix} \mathscr {L}_1^* \lambda _1 \\ \mathscr {L}_2^* \lambda _2 \\ \mathscr {L}_3^* \lambda _3 \\ \mathscr {L}_4^* \lambda _4 \\ \mathscr {L}_5^* \lambda _5 \\ \end{pmatrix} + \varvec{M}^T \begin{pmatrix} \lambda _1 \\ \lambda _2 \\ \lambda _3 \\ \lambda _4 \\ \lambda _5 \\ \end{pmatrix}, \end{aligned}$$

and:

$$\begin{aligned} \begin{pmatrix} \mathscr {L}_1^* \lambda _1 \\ \mathscr {L}_2^* \lambda _2 \\ \mathscr {L}_3^* \lambda _3 \\ \mathscr {L}_4^* \lambda _4 \\ \mathscr {L}_5^* \lambda _5 \\ \end{pmatrix} = \begin{pmatrix} -(\lambda _1)_t - \nabla \cdot (\alpha \nabla \lambda _1) \\ -(\lambda _2)_t - \nabla \cdot (\alpha _I \nabla \lambda _2) \\ -(\lambda _3)_t - \nabla \cdot (\alpha \nabla \lambda _3) \\ -(\lambda _4)_t - \nabla \cdot (\alpha _v \nabla \lambda _4) \\ -(\lambda _5)_t - \nabla \cdot (\alpha _v \nabla \lambda _5) \\ \end{pmatrix}, \end{aligned}$$

with final time conditions given by (7) and boundary conditions by (8).

1.3 Optimal control characterization

We now derive an expression for an optimal control $u^*$ as a function of the state and adjoint variables. The derivative of the map $u \rightarrow J(u)$ at $u^*$ in the direction $\ell$ is:

$$\begin{aligned} \lim _{\epsilon \rightarrow 0^+} \dfrac{J(u^*+\epsilon \ell ) - J(u^*)}{\epsilon } \ge 0, \end{aligned}$$

with:

$$\begin{aligned} \begin{aligned} J(u^*+\epsilon \ell )&= \int _Q \left[ c_1 I^\epsilon + c_2 (u^* + \epsilon \ell ) S^\epsilon + c_3 ( u^* + \epsilon \ell )^2 \right] \mathrm {d}\varvec{x} \mathrm {d}t \\&= \int _Q \left[ c_1 I^\epsilon + c_2 u^* S^\epsilon + \epsilon c_2 \ell S^\epsilon + c_3 (u^*)^2 + 2 c_3 u^* \epsilon \ell + c_3 \epsilon ^2 \ell ^2 \right] \mathrm {d}\varvec{x} \mathrm {d}t. \\ J(u^*)&= \int _Q \left[ c_1 I^\epsilon + c_2 u^* + c_3 ( u^*)^2 \right] \mathrm {d}\varvec{x} \mathrm {d}t. \end{aligned} \end{aligned}$$

Using the sensitivity and adjoint systems we find a characterization for $u^*$:

$$\begin{aligned} \begin{aligned} 0&\le \lim _{\epsilon \rightarrow 0^+} \dfrac{J(u^*+\epsilon \ell ) - J(u^*)}{\epsilon } \\ 0&\le \lim _{\epsilon \rightarrow 0^+} \int _Q \left[ c_1 \dfrac{I^\epsilon -I}{\epsilon } + c_2 u^* \dfrac{S^\epsilon -S}{\epsilon } + c_2 \ell S^\epsilon + 2 c_3 u^* \ell + c_3 \epsilon \ell ^2 \right] \mathrm {d}\varvec{x} \mathrm {d}t \\ 0&\le \int _Q \left[ c_1 \psi _2 + c_2 u^* \psi _1 + c_2 \ell S^* + 2 c_3 u^* \ell \right] \mathrm {d}\varvec{x} \mathrm {d}t \\ 0&\le \int _Q \left[ \left( \psi _1, \psi _2, \psi _3, \psi _4, \psi _5 \right) \left( c_2 u^*, c_1, 0, 0, 0 \right) ^T + \ell \left( c_2 S^* + 2 c_3 u^* \right) \right] \mathrm {d}\varvec{x} \mathrm {d}t \\ 0&\le \int _Q \left[ \left( \psi _1, \psi _2, \psi _3, \psi _4, \psi _5 \right) \mathscr {L}^*\left( \lambda _1,\lambda _2,\lambda _3,\lambda _4,\lambda _5 \right) ^T + \ell \left( c_2 S^* + 2 c_3 u^* \right) \right] \mathrm {d}\varvec{x} \mathrm {d}t \\ 0&\le \int _Q \left[ \left( \lambda _1,\lambda _2,\lambda _3,\lambda _4,\lambda _5 \right) \mathscr {L}\left( \psi _1, \psi _2, \psi _3, \psi _4, \psi _5 \right) ^T + \ell \left( c_2 S^* + 2 c_3 u^* \right) \right] \mathrm {d}\varvec{x} \mathrm {d}t \\ 0&\le \int _Q \left[ \left( \lambda _1,\lambda _2,\lambda _3,\lambda _4,\lambda _5 \right) \left( - \ell S^*, 0, \ell S^*,0,0 \right) ^T + \ell \left( c_2 S^* + 2 c_3 u^* \right) \right] \mathrm {d}\varvec{x} \mathrm {d}t \\ 0&\le \int _Q \left[ -\ell \lambda _1 S^* + \ell \lambda _3 S^* + \ell \left( c_2 S^* + 2 c_3 u^* \right) \right] \mathrm {d}\varvec{x} \mathrm {d}t \\ 0&\le \int _Q \ell \left[ \left( -\lambda _1 + \lambda _3 + c_2 \right) S^* + 2 c_3 u^* \right] \mathrm {d}\varvec{x} \mathrm {d}t. \\ \end{aligned} \end{aligned}$$

On the set where $u_{\min }< u^*(x, t) < u_{\max }$, the variation $\ell$ can be an $L^{\infty }$ function with arbitrary sign, and thus on this set, we obtain:

$$\begin{aligned} u^* = \dfrac{(\lambda _1 - \lambda _3 - c_2)S^*}{2c_3}. \end{aligned}$$

Due to the boundedness $u_{\min } \le u \le u_{\max }$, and taking variations $\ell$ with appropriate signs when $u^*$ is at the lower or upper bounds, we can obtain the following optimal control characterization:

$$\begin{aligned} u^* = \min \left( u_{\max }, \max \left( \dfrac{(\lambda _1 - \lambda _3 - c_2)S^*}{2c_3}, u_{\min } \right) \right) . \end{aligned}$$