Abstract
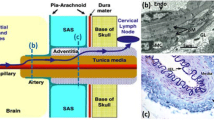
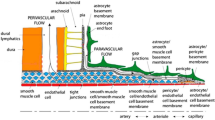
Beta-amyloid accumulation within arterial walls in cerebral amyloid angiopathy is associated with the onset of Alzheimer’s disease. However, the mechanism of beta-amyloid clearance along peri-arterial pathways in the brain is not well understood. In this study, we investigate a transport mechanism in the arterial basement membrane consisting of forward-propagating waves and their reflections. The arterial basement membrane is modeled as a periodically deforming annulus filled with an incompressible single-phase Newtonian fluid. A reverse flow, which has been suggested in literature as a beta-amyloid clearance pathway, can be induced by the motion of reflected boundary waves along the annular walls. The wave amplitude and the volume of the annular region govern the flow magnitude and may have important implications for an aging brain. Magnitudes of transport obtained from control volume analysis and numerical solutions of the Navier–Stokes equations are presented.











Similar content being viewed by others
References
Abbott NJ (2004) Evidence for bulk flow of brain interstitial fluid: significance for physiology and pathology. Neurochem Int 45(4):545–552
Alastruey J, Parker KH, Sherwin SJ (2012) Arterial pulse wave haemodynamics. In: Anderson. 11th international conference on pressure surges, pp 401-442
Alzheimer’s Association (2010) 2010 Alzheimer’s disease facts and figures. Alzheimer’s Dement 6(2):158-194
Bilston L, Flecther D, Brodbelt A, Stoody M (2003) Arterial pulsation-driven cerebrospinal fluid flow in the perivascular space: a computational model. Comput Methods Biomech Biomed Eng 6(4):235–241
Carare RO, Bernardes-Silva M, Newman T, Newman T, a, Page a M, Nicoll J a R, Perry VH, Weller RO (2008) Solutes, but not cells, drain from the brain parenchyma along basement membranes of capillaries and arteries: significance for cerebral amyloid angiopathy and neuroimmunology. Neuropathol Appl Neurobiol 34(2):131–144
Elmore WC, Heald MA (1969) Physics of waves. Courier Corporation, New York
Farkas E, Luiten PG (2001) Cerebral microvascular pathology in aging and Alzheimer’s disease. Prog Neurobiol 64(6):575–611
Fung YC (1984) Biodynamics circulation. Springer, New York
Hawkes CA, Hartig W, Kacza J, Schliebs R, Weller RO, Nicoll JA, Carare RO (2011) Perivascular drainage of solutes is impaired in the ageing mouse brain and in the presence of cerebral amyloid angiopathy. Acta Neuropathol 121(4):431–443
Hawkes CA, Gatherer M, Sharp MM, Dorr A, Yuen HM, Kalaria R, Weller RO, Carare RO (2013) Regional differences in the morphological and functional effects of aging on cerebral basement membranes and perivascular drainage of amyloid- from the mouse brain. Aging cell 12(2):224–236
Hughes TM, Kuller LH, Barinas-Mitchell EJ, McDade EM, Klunk WE, Cohen AD, Mathis CA, DeKosky ST, Price JC, Lopez OL (2014) Arterial stiffness and beta-amyloid progression in nondemented elderly adults. JAMA Neurol 71(5):562–568
Iliff JJ, Wang MH, Liao YH, Plog BA, Peng WG, Gundersen GA, Gundersen GA, Benveniste H, Vates GE, Deane R, Goldman SA, Nagelhus EA, Nedergaard M (2012) A paravascular pathway facilitates CSF flow through the brain parenchyma and the clearance of interstitial solutes, including amyloid beta. Sci Transl Med 4(147):147ra111
Iliff JJ, Wang MH, Zeppenfeld DM, Venkataraman A, Plog BA, Liao YH, Deane R, Nedergaard M (2013) Cerebral arterial pulsation drives paravascular CSF-interstitial fluid exchange in the murine brain. J Neurosci 33(46):18190–18199
Kamath S (1981) Observations on the length and diameter of vessels forming the circle of Willis. J Anat 133(3):419–423
Knopf PM, Cserr HF, Nolan SC, Wu TY, Harlingberg CJ (1995) Physiology and immunology of lymphatic drainage of interstitial and cerebrospinal-fluid from the brain. Neuropathol Appl Neurobiol 21(3):175–180
Krings T, Mandell DM, Kiehl TR, Geibprasert S, Tymianski M, Alvarez H, terBrugge KG, Hans FJ (2011) Intracranial aneurysms: from vessel wall pathology to therapeutic approach. Nat Rev Neurol 7(10):547–559
Li JK (2004) Dynamics of the vascular system. World Scientific, Singapore
Mawuenyega KG, Sigurdson W, Ovod V, Munsell L, Kasten T, Morris JC, Yarasheski KE, Bateman RJ (2010) Decreased clearance of CNS beta-amyloid in Alzheimer’s disease. Science 330(6012):1774–1774
Nichols WW (2005) Clinical measurement of arterial stiffness obtained from noninvasive pressure waveforms. Am J Hypertens 18(1):3S–10S
Nichols W, O’Rourke M, Vlachopoulos C (2011) McDonald’s blood flow in arteries: theoretical, experimental and clinical principles. CRC Press, Boca Raton
Papageorgiou GL, Jones BN, Redding VJ, Hudson N (1990) The area ratio of normal arterial junctions and its implications in pulse waves. Cardiovasc Res 24(6):478–484
Preston SD, Steart PV, Wilkinson A, Nicoll JAR, Weller RO (2003) Capillary and arterial cerebral amyloid angiopathy in Alzheimer’s disease : defining the perivascular route for the elimination of amyloid beta from the human brain. Neuropathol Appl Neurobiol 29(2):106–118
Schley D, Carare-Nnadi R, Please CP, Perry VH, Weller RO (2006) Mechanisms to explain the reverse perivascular transport of solutes out of the brain. J Theor Biol 238(4):962–974
Tanzi RE, Moir RD, Wagner SL (2004) Clearance of Alzheimer’s A beta peptide: the many roads to perdition. Neuron 43(5):605–608
Wang P, Olbricht WL (2011) Fluid mechanics in the perivascular space. J Theor Biol 274(1):52–57
Weller R, Subash M, Preston S, Mazanti I, Carare R (2008) Perivascular drainage of amyloid-\(\upbeta \) peptides from the brain and its failure in cerebral amyloid angiopathy and Alzheimer’s disease. Brain Pathol 18:253–266
Weller RO, Galea I, Carare RO, Minagar a (2010) Pathophysiology of the lymphatic drainage of the central nervous system: implications for pathogenesis and therapy of multiple sclerosis. Pathophysiology 17(4):295–306
Yang ST, Mayhan WG, Faraci FM, Heistad DD (1991) Endothelium-dependent responses of cerebral blood-vessels during chronic hypertension. Hypertension 17(5):612–618
Yao W, Li YB, Ding GH (2012) Interstitial fluid flow: the mechanical environment of cells and foundation of Meridians. Evid Based Complement Alternat Med 2012:853516. doi:10.1155/2012/853516
Acknowledgments
M.C. would like to acknowledge the support of the Clifford D. Clark Diversity Fellowship. J.D.S., P.R.C., and P.H. would like to acknowledge the State Univeristy of New York at Binghamton University Interdisciplinary Collaborative Grant program for supporting this work.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Momentum correction factor for an annulus
The dimensionless momentum-flux correction factor at a control surface k is
where \(u_{k}\) is the velocity profile at the control surface. \(\beta _{k}=1\) represents a uniform flow profile while a parabolic flow profile leads to \(\beta _{k}> 1\). The velocity profile for a steady, incompressible, laminar, unidirectional flow in an annulus with no-slip boundary conditions is
where dp/dx is the local pressure gradient and \(\mu \) is the fluid viscosity, and
Appendix 2: Derivation of the control volume flow rate formula
Equation (8) can be re-written in terms of \(\bar{{u}}_{2}\) and \(\alpha \),
where \(\bar{u}_{2}\) must remain real at all times and requires \({dP}/{dt}<\bar{{u}}_{1}^{2}\beta _{1} A_1\). The periodic nature of the rate of change of momentum in the control volume allows us to infer that \(\left| {{dP}/{dt}} \right| <\bar{{u}}_1 ^{2}\beta _1 A_1\). We thus employ a binomial expansion of Eq. (16),
Since at any given instant of time a velocity must be unique, we determine the sign in Eq. (17) by considering the leading order term and substitute it into Eq. (7), which leads to
The minus sign solution in Eq. (18) is physically unreasonable because during each deformation cycle, there must exist instances when \(\alpha =1\). Thus, at those instances
which leads to singularity for \(\bar{{u}}_1\). This indicates that the only plausible sign for Eq. (17) must be negative and
When the two leading order terms in Eq. (19) are considered and substituted into Eq. (7), it yields a quadratic equation in terms of \(\bar{{u}}_1\),
whose solution is
Again, \(\bar{{u}}_1\) must remain real at all times, and given the periodic nature of dP/dt, we can infer that
Once again by invoking the binomial series expansion of the square root term in Eq. (21) and keeping the two leading order terms, we get
Numerical evaluation of Eq. (23) requires us to obtain an approximate expression for dP/dt. We define a spatially averaged velocity in the x-direction as \(u_{avg,S}=(1/V) \int \int \int (\mathbf{u}\cdot \hat{{x}})dV = P/V\) where u is velocity field vector and \(\hat{{x}}\) is the unit direction vector pointing in the axial direction. Since the flow is periodic, a velocity averaged over a space of one wavelength is approximately equal to a timed-averaged velocity \(u_{avg,T}\) at \(A_{1}\) over one period, or
Given that \(u_{avg,T}\) is not a function of time,
Substituting Eq. (25) into Eq. (23) yields
Equation (26) shows two possible solutions for \(Q_{\textit{CV}}\), which also must be unique. We first consider Eq. (26) with the negative sign, which yields
Rearranging Eq. (27) leads to \(Q_{\textit{CV}}=0\), regardless of the annular deformation, which is not physically plausible given that a periodically deforming control volume due to traveling boundary waves should result in non-zero overall flow. Choosing the positive sign in Eq. (26) thus leads to Eq. (7).
Rights and permissions
About this article
Cite this article
Coloma, M., Schaffer, J.D., Carare, R.O. et al. Pulsations with reflected boundary waves: a hydrodynamic reverse transport mechanism for perivascular drainage in the brain. J. Math. Biol. 73, 469–490 (2016). https://doi.org/10.1007/s00285-015-0960-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00285-015-0960-6