Model for disease dynamics of a waterborne pathogen on a random network

Abstract

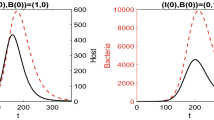
A network epidemic SIWR model for cholera and other diseases that can be transmitted via the environment is developed and analyzed. The person-to-person contacts are modeled by a random contact network, and the contagious environment is modeled by an external node that connects to every individual. The model is adapted from the Miller network SIR model, and in the homogeneous mixing limit becomes the Tien and Earn deterministic cholera model without births and deaths. The dynamics of our model shows excellent agreement with stochastic simulations. The basic reproduction number $\mathcal {R}_0$ is computed, and on a Poisson network shown to be the sum of the basic reproduction numbers of the person-to-person and person-to-water-to-person transmission pathways. However, on other networks, $\mathcal {R}_0$ depends nonlinearly on the transmission along the two pathways. Type reproduction numbers are computed and quantify measures to control the disease. Equations giving the final epidemic size are obtained.

Appendix A The homogeneous mixing limit

Here we show that our model (14) becomes the Tien and Earn (2010) SIWR model without births and deaths in a homogeneously mixing population, i.e., on a complete graph. On such a complete graph with $N\gg 1$ individuals, every node has degree $N-1$. Thus

$$\begin{aligned} S&=\Psi (\theta )\phi _W=\theta ^{N-1}\phi _W , \\ \frac{d\theta }{dt}&=-\beta _I \phi , \\ \frac{d\phi }{dt}&=-\beta _I \phi -\gamma \phi +(N-2)\theta ^{N-3}\beta _I\phi \phi _W + \theta ^{N-2}\beta _W W\phi _W. \end{aligned}$$

Thus using (14c),

$$\begin{aligned} \frac{dS}{dt}&=(N-1)\theta ^{N-2}(-\beta _I \phi )\phi _W+ \theta ^{N-1}(-\beta _W W\phi _W) \\&=-qS\frac{\phi }{\theta }-\beta _W W S, \end{aligned}$$

where $q=\beta _I(N-1)$.

For a complete graph, $I$ should be equal to $\phi /\theta$. This can be verified by computing $\frac{d}{dt}\left( \frac{\phi }{\theta }\right)$ and comparing with $dI/dt=qSI+\beta _W WS-\gamma I$.

$$\begin{aligned} \frac{d}{dt}\frac{\phi }{\theta }&= \frac{1}{\theta }\frac{d\phi }{dt}-\frac{\phi }{\theta ^2}\frac{d\theta }{dt} \\&= -\beta _I \frac{\phi }{\theta }-\gamma \frac{\phi }{\theta }+(N-2)\theta ^{N-3}\beta _I \frac{\phi }{\theta }\phi _W+\theta ^{N-3}\beta _W W\phi _W +\beta _I\frac{\phi ^2}{\theta ^2} \\&=[\frac{(N-2)q}{N-1}\frac{\phi }{\theta }+\beta _W W]\frac{S}{\theta ^2}-\frac{q}{N-1}\frac{\phi }{\theta } -\gamma \frac{\phi }{\theta } +\frac{q\phi ^2}{(N-1)\theta ^2}\\&\rightarrow [q\frac{\phi }{\theta }+\beta _W W]\frac{S}{\theta ^2}-\gamma \frac{\phi }{\theta }\,, \end{aligned}$$

as $N\rightarrow \infty$. This agrees with $dI/dt$ provided that $\theta (t)\rightarrow 1$ for any time $t$ as $N\rightarrow \infty$. This can be proved from (14b):

$$\begin{aligned} \frac{d\theta }{dt} =-\beta _I\phi =-\frac{q}{N-1}\phi \ge -\frac{q}{N-1}, \end{aligned}$$

and thus with $\theta (0)=1$, for any $t$, $\theta \ge 1-qt/(N-1)\rightarrow 1$ as $N\rightarrow \infty$. Thus, on a complete network, our model becomes model (1) as the population size $N\rightarrow \infty$.

In fact, Miller [2011, Appendix A] showed that the limit holds for an SIR model if all individuals have the same degree and the degree approaches infinity. In addition, Miller and Volz (2013) relaxed the condition to be the average degree $\left\langle k\right\rangle \rightarrow \infty$ while $\left\langle k^4\right\rangle /\left\langle k\right\rangle ^4\rightarrow 1$. That is, the limit holds even if the network does not approach a complete graph. This same argument applies here.