1 Introduction

Exotic species, commonly referred to as invasive species, are defined as any species, capable of propagating themselves into a nonnative environment. Once established, they can be extremely difficult to eradicate, or even manage (Hill and Cichra 2005; Shafland and Foote 1979). Numerous cases of environmental harm and economic losses are attributed to various invasive species (Harmful 1993; Myers et al. 2000). Some well-known examples of these species include the burmese python in southern regions of the United States, the cane toad in Australia, and the sea lamprey and round goby in the Great Lakes region in the northern United States (Gutierrez 2005). The cane toad was brought into Australia from Hawaii in 1935 in order to control the cane beetle. These have multiplied rapidly since then, and are currently Australia’s worst invasive species (Philips and Shine 2004). The sea lamprey entered the great lakes in the 1800s, through shipping canals (Bryan et al. 2005), and these predators have caused a severe decline in lake fish populations, adversely affecting local fisheries. The burmese python population has been on the rise exponentially, in the Florida glades, since the 1980s. Much of this is attributed to the exotic pet trade in Florida. These invaders have had quite a negative impact on the local ecology, and climatic factors might support their spread to a third of the United States (Rodda et al. 2005). Apart from being considered one of the greatest threats to biodiversity, invasive species cause agricultural losses worldwide in the range of several 100 billion dollars (Pimentel et al. 2005; Gutierrez 2005). Despite the magnitude of threats they pose, there have been no conclusive results to eradicate or contain these species in real scenarios, in the wild.

A possible approach to the containment of these invasive species is the use of a feasible biological control. It is well-known that the size of a population can be seriously affected as a result of shifting the sex ratio (Hamilton 1976). The sterile insect technique (SIT), works via the introduction of large quantities of sterile males, into a target population, to compete with fertile males in mating (Knipling 1955). Mating with sterile males does not produce any progeny, and the goal is to try and shift the sex ratio so that there is an abundance of males, leading to less and less number of females over time. The method is commonly used in Florida, to control crop damage via Mediterranean fruit flies (Klassen and Curtis 2005). This in essence, is the underlying principle for a number of recently proposed models (Howard et al. 2004; Gutierrez and Teem 2006; Bax and Thresher 2009), that use genetic modification to control invasive fish species. Among these models, the Daughterless Carp (Bax and Thresher 2009) and the Trojan Y-Chromosome (TYC) (Gutierrez and Teem 2006), have been particularly well studied. The first strategy aims at causing extinction via the release of individuals with chromosomal insertions of aromatase inhibitors. The latter strategy tries to cause extinction via the constant release of sex-reversed supermales, denoted as \(r\) in (2.1), into a target population, see Fig. 1. The idea behind the TYC strategy, is that mating with the sex-reversed supermales results in only male or supermale progeny, leading to less and less number of females over time, and ultimately driving the female population to zero. This will thus lead to extinction of the population. Note that the TYC strategy only works for a few species with \(XY\) sex determination system, that are capable of producing viable progeny during the sex reversal process. Thus, it is not applicable to all the species mentioned earlier. The TYC eradication strategy was proposed by Gutierrez and Teem (2006). Parshad and Gutierrez (2010) rigorously proved the existence of a global attractor for the model derived in (Gutierrez and Teem 2006), with the inclusion of diffusion. In particular, they show that the attractor possesses the extinction state, if the introduction of sex-reversed supermales is large enough. However, these works do not explore the full structure of the attractor, via a rigorous stability and bifurcation analysis. Changing the sex ratio of a population seems difficult to achieve in practice, there have been a number of studies to this end (Nagler et al. 2001). It has also been reported that environmental pressure for masculinization would lead to extinction of fish populations with a XY sex-determination system (Hurley et al. 2004). Masculinization by exposure to androgens has been reported in the wild (Katsiadakiand et al. 2002), and is common in the salmon industry to produce an all-male stock (Hunter and Donaldson 1983).

Fig. 1
figure 1

The pedigree tree of the TYC model (that demonstrates Trojan Y-chromosome eradication strategy). a Mating of a wild-type XX female (f) and a wild-type XY male (m). b Mating of a wild-type XY male (m) and a sex-reversed YY female (r). c Mating of a wild-type XX female (f) and a YY supermale (s). d Mating of a sex-reversed YY trojan female (r) and a YY supermale (s). Red color represents wild types, and white color represents phenotypes (color figure online)

Full size image

In order to develop successful physical and biological controls for exotic fish species, the dynamics of fish populations and eradication strategies constructed on the basis of these dynamics have to be studied and further understood. The goal of this work is to pursue a number of questions, that are not addressed in (Gutierrez and Teem 2006; Parshad and Gutierrez 2010). These earlier works in essence, show that extinction is possible if the rate of release \(\mu \), of sex-reversed supermales is large enough. They do not address the case of small \(\mu \). We now ask the following question: what happens if the introduction of the feminized supermales is stopped? Can the fish population possibly recover, from low levels, instead of going to the extinction state? Any eradication strategy, with potential to be implemented into a management practice, cannot possibly sustain the constant introduction of genetically modified organisms into a target population, particularly over a large spatial domain. Thus, a rigorous stability analysis of the model, in order to understand the specific structure of the attractor has to be performed, in the case this release rate \(\mu >0\), and \(\mu =0\). In particular, the extinction or recovery, and their connection with the range of \(\mu \), has to be rigorously identified. This is the first contribution of the current work. Next, the Allee effect (a well-known phenomenon from population dynamics, defined as a positive correlation between population density and individual fitness) (Odum and Allee 1954; Stephens and Sutherlan 1999) is incorporated into the current TYC model. Turing instability is also explored in the context of the TYC model.

This article is organized as follows. Section 2 introduces the TYC eradication strategy and the TYC model developed in (Gutierrez and Teem 2006). Section 3 presents the equilibrium and stability analysis of the TYC model. The Allee effect is studied in Sect. 4. The basin of attraction of the extinction state is demonstrated in Sect. 5 in terms of a reduced two-dimensional TYC model, the full TYC model when \(\mu =0\), and a reduced two-dimensional TYC model with the inclusion of an Allee effect. In Sect. 6, we show that incorporating diffusive spatial spread does not give rise to a Turing instability. Concluding remarks are given in Sect. 7.

2 Model description

Gutierrez and Teem (2006) proposed a mathematical model of the Trojan Y-Chromosome (TYC) eradication strategy for invasive fish species. The idea behind this strategy is to eliminate the wild-type female fish from a population, by introducing a sex-reversed “Trojan” female fish, into the population. Mating with the trojan, only leads to male, or supermale progeny. This will lead to lesser and lesser wild-type females over time, ultimately leading to their eradication, and thus causing the population to go extinct. The strategy relies on two facts: (1) the wild-type invasive fish species are required to have an XY sex-determination system, that is, sex is determined by the presence of a Y chromosome in a fish species; (2) the sex change of genetic males to females and of females to males can be made through chemical induced genetic manipulation, such as hormone treatments.

Gutierrez and Teem (2006) considered the Nile tilapia as an example. Their TYC model describes the dynamics of four phenotype/genotype variants of the invasive fish species: genotype XX females, genotype XY males, phenotype YY supermales and phenotype sex-reversed YY females, denoted as \(f,m,s\) and \(r\), respectively. The eradication strategy works as follows. A sex-reversed trojan female \((r)\), carrying two Y Chromosomes, is introduced into a wild-type invasive fish population comprised of wild-type males \((m)\) and females \((f)\). Mating between a phenotype female \((r)\) and a genotype male \((m)\) produces a disproportionate number of male fish \(m\). The high incidence of males decreases the sex ratio of females to males. Ultimately, the wild-type females would be eliminated from the population. As a consequence, the wild-type invasive population goes extinct.

It follows from the pedigree tree of the TYC model illustrated in Fig. 1, that the equation describing the time evolution of the system can be written as:

$$\begin{aligned} \dfrac{df}{dt}&= \dfrac{1}{2} f m \beta L-\delta f,\nonumber \\ \dfrac{dm}{dt}&= \Big (\dfrac{1}{2} f m + \dfrac{1}{2} rm + f s\Big ) \beta L-\delta m,\nonumber \\ \dfrac{ds}{dt}&= \Big (\dfrac{1}{2} r m + rs \Big ) \beta L-\delta s,\nonumber \\ \dfrac{dr}{dt}&= \mu -\delta r, \end{aligned}$$
(2.1)

where \(f,m,s,r\) define the number of individuals in each associated class; positive constants \(\beta \) and \(\delta \) represent the per capita birth and death rates, respectively; nonnegative constant \(\mu \) denotes the rate at which the sex-reversed YY females \(r\) are introduced; \(L\) is a logistic term given by

$$\begin{aligned} L = 1-\dfrac{f+m+s+r}{K}, \end{aligned}$$
(2.2)

with K interpreted as the carrying capacity of the ecosystem.

3 Equilibrium analysis of the TYC model

Let \((f^{*},m^{*},s^{*}, r^{*})^{T}\) denote an equilibrium of model (2.1). We are interested in the solution in the region \(\varOmega :=\{(f,m,s, r)^{T}: 0\le f,m,s,r\le K\}\).

3.1 The case \(\mu >0\)

Assume that the sex-reversed trojan females are introduced into the wild at the rate \(\mu >0\). We study the dynamics of the associated TYC model.

3.1.1 Determination of equilibria

Case 1 Assume \(f^{*}=0.\)

An equilibrium with \(f^{*}=0\) describes a steady state of (2.1) at which wild-type XX females are eradicated. Let

$$\begin{aligned} \varGamma =\beta \mu ^2-\beta K \delta \mu + K \delta ^3. \end{aligned}$$
(3.1)

If \(\varGamma \ge 0\), Eq. (2.1) has only one equilibrium that satisfies \(f^{*}=0\), namely, \(\Big (0,0,0,\dfrac{\mu }{\delta }\Big )^{T}\). Otherwise, if \(\varGamma <0\), Eq. (2.1) has two equilibria with \(f^{*}=0\). One is \(\Big (0,0,0,\dfrac{\mu }{\delta }\Big )^{T}\), and the other one is \(\Big (0,0, K\Big (1-\dfrac{\delta ^2}{\mu \beta }\Big )-\dfrac{\mu }{\delta },\dfrac{\mu }{\delta }\Big )^{T}\). Clearly, if \(f^{*}>0,\,m^{*}>0\) and \(r^{*}>0\), then \(s^{*}>0\), and \(s^{*}=0\) is not a solution of biological meaning.

Case 2 Assume \(f^{*}>0\).

By direct computations, we find that the equilibrium satisfies

$$\begin{aligned} f^{*}&= \dfrac{(r^{*})^{2}(r^{*}+s^{*})}{s^{*}(s^{*}-r^{*})},\nonumber \\ m^{*}&= \dfrac{2 r^{*}s^{*}}{s^{*}-r^{*}},\nonumber \\ r^{*}&= \dfrac{\mu }{\delta }, \end{aligned}$$
(3.2)

where \(s^{*}\) satisfies

$$\begin{aligned} s(a s^3 +b s^2 + c s+d )=0, \end{aligned}$$
(3.3)

with \(a=a(r^{*}):=r^{*}\beta ,\,b=b(r^{*}):= 2\beta (r^{*})^{2} - \beta K r^{*} +\delta K,\,c=c(r^{*}):= \beta K (r^{*})^{2} - 2 \delta K r^{*}\), and \(d=d(r^{*}):=\beta (r^{*})^4 + K \delta (r^{*})^2 \).

If \(\mu >0\), assumptions of model (2.1) on the parameter values yield \(a>0\) and \(d>0\). Clearly, \(s^{*}> r^{*}>0\) is required for the equilibrium of model (2.1) to be in the region \(\varOmega \).

Let \(r_b^{\pm }=\dfrac{K}{4}\pm \sqrt{\Big (\dfrac{K}{4}\Big )^2-\dfrac{\delta K}{2\beta }}\) and \(r_c=\dfrac{2 \delta }{\beta }\). It is easy to verify that \(r_b^{\pm }\) and \(r_c\) are the nonzero roots of \(b(r^{*})=0\) and \(c(r^{*}) =0\), respectively.

We define \(\alpha = \beta K /{2\delta }\).

Lemma 3.1

(a) If \(\alpha =4,\,r_b^{-}=r_c=r_b^{+}\), (b) If \(\alpha >4\), then \(r_b^{-}<r_c<r_b^{+}.\)

Proof

One can easily verify the result by direct calculation. \(\square \)

For simplicity, we write \(\varDelta =18 a b c d-4 b^3 d+(bc)^2-4a c^3-27 (a d)^2\). In fact, \(\varDelta \) is the determinant of a cubic equation \(a s^3 +b s^2 + c s+d=0\). The three cases for this determinant are well known.

Proposition 3.1

Assume that \(\varDelta >0\).

  1. (a)

    If \(\alpha >4\), then Eq. (3.3) has two positive roots for \(\dfrac{\mu }{\delta }< r_b^+\), and no positive roots for \(\dfrac{\mu }{\delta }\ge r_b^{+}\).

  2. (b)

    If \(\alpha \le 4\), then Eq. (3.3) has two positive roots for \(\dfrac{\mu }{\delta }< r_c\), and no positive roots for \(\dfrac{\mu }{\delta }\ge r_c\).

Proof

We define the term in parentheses of Eq. (3.3) to be

$$\begin{aligned} g(s)=a s^3 +b s^2 + c s+d. \end{aligned}$$
(3.4)

By \(a>0\) and \(\varDelta >0\), Eq. (3.4) has three distinct real roots. Moreover, none of the roots can be zero because \(d\ne 0\).

Case (a) \(\alpha >4\). By Lemma 3.1, we have \(r_b^{-}<r_c<r_b^{+}.\)

  1. (1)

    Assume \(r^{*}=\mu /{\delta }\in (0, r_b^{-})\). Then \(b>0\) and \(c<0\). The signs of the coefficients of \(g(s)\) and \(g(-s)\) are

    $$\begin{aligned} \text{ sign }(a,b,c,d)=(+,+,-,+), \end{aligned}$$
    (3.5)

    and

    $$\begin{aligned} \text{ sign }(-a,b,-c,d)=(-,+,+,+), \end{aligned}$$
    (3.6)

    respectively. So there are \(2\) sign changes in \(g(s)\) and \(1\) sign change in \(g(-s)\). By Descartes’ rule of signs, we see that \(g(s)=0\) has either \(2\) or \(0\) positive roots and exactly \(1\) negative root. Since \(g(s)=0\) has three nonzero real roots, the roots have to be comprised of \(2\) positive ones and \(1\) negative one.

  2. (2)

    Assume \(r^{*}\in [r_b^{-}, r_b^{+})\). If \(r^{*}=r_b^{-}\), then \(b=0\) and \(c<0\). If \(r^{*}\in (r_b^{-}, r_c)\), then \(b<0\) and \(c<0\). If \(r^{*}=r_c\), then \(b<0\) and \(c=0\). If \(r^{*}\in (r_c, r_b^{+})\). then \(b<0\) and \(c>0\). By similar arguments, we can show that \(g(s)\) has two positive zeros.

  3. (3)

    Assume \(r^{*}\in [r_b^{+}, \infty )\). If \(r^{*}= r_b^{+}\), then \(b=0\) and \(c>0\). If \(r^{*}> r_b^{+}\), then \(b>0\) and \(c>0\). Since there are no changes of sign in the coefficients, there are no positive zeros for \(g(s)\).

Case (b) \(\alpha \le 4\). Then \(b\ge 0\). Similarly, we can show that:

  1. (1)

    if \(r^{*}<r_c\), then \(c<0\) and \(g(s)\) has two positive zeros;

  2. (2)

    if \(r^{*}\ge r_c\), then \(c\ge 0\) and \(g(s)\) has no positive zeros.

The results follow, since all nonzero roots of (3.3) satisfy \(g(s)=0\). \(\square \)

Proposition 3.2

Assume that \(\varDelta =0\).

  1. (a)

    If \(\alpha >4\), then Eq. (3.3) has either zero or two positive roots for \(\dfrac{\mu }{\delta }< r_b^+\), and no positive roots for \(\dfrac{\mu }{\delta }\ge r_b^{+}\).

  2. (b)

    If \(\alpha \le 4\), then Eq. (3.3) has either zero or two positive roots for \(\dfrac{\mu }{\delta }< r_c\), and no positive roots for \(\dfrac{\mu }{\delta }\ge r_c\).

Proof

If \(\varDelta =0\), Eq. (3.4) has a multiple root and all its roots are real. The results follow from Descartes’ rule of signs. \(\square \)

Proposition 3.3

Assume that \(\varDelta <0\). Then Eq. (3.3) has no positive roots.

Proof

If \(\varDelta <0,\,g(s)=0\) has one real root and two complex conjugate roots. The results can be shown by Descartes’ rule of signs. \(\square \)

3.1.2 Stability of equilibria

Linearize system (2.1) at the equilibria. The associated Jacobian matrix is given by

$$\begin{aligned} \mathbf J _q \!=\! \left[ \begin{array}{llll} \dfrac{\beta }{2} m^{*} L^{*}-\xi -\delta &{}\quad \dfrac{\beta }{2} f^{*} L^{*}-\xi &{}\quad -\xi &{}-\xi \\ (m^{*}/2+s^{*})\beta L^{*}-\eta &{}\quad (f^{*}/2+r^{*}/2)\beta L^{*}-\eta -\delta &{}\quad \beta f^{*}L^{*}-\eta &{}\quad m^{*} \beta L^{*}/2-\eta \\ -\kappa &{} {\beta }r^{*}L^{*}/2-\kappa &{}\quad \beta r^{*}L^{*} -\kappa -\delta &{}\quad (m^{*}/2+s^{*})\beta L^{*}-\kappa \\ 0&{}\quad 0&{}\quad 0&{}\quad -\delta \end{array}\!\right] \nonumber \\ \end{aligned}$$
(3.7)

where \(L^{*}=1-(f^{*}+m^{*}+s^{*}+r^{*})/{K},\,\xi ={\beta }f^{*} m^{*}/(2K),\,\eta ={\beta }(f^{*}m^{*}+ r^{*}m^{*}+2f^{*}s^{*})/(2K)\) and \(\kappa =\beta r^{*}\Big (m^{*}+2 s^{*}\Big )/(2K)\).

The equilibrium of model (2.1) that satisfies \(f^{*}=0\) is of the form of \((0,0,s^{*}, r^{*})^{T}\). Evaluate (3.7) at \((0,0,s^{*}, r^{*})^{T}\). We find the associated characteristic equation can be written as:

$$\begin{aligned} \left( \lambda +\delta \right) \left[ \lambda -\left( \dfrac{\beta }{2}r^{*}L^{*}-\delta \right) \right] \left[ \lambda -\left( \beta r^{*}\left( L^{*}-\dfrac{s^{*}}{2K}\right) \!-\! \delta \right) \right] \left( \lambda +\delta \right) \!=\!0,\qquad \end{aligned}$$
(3.8)

and the corresponding eigenvalues are given by

$$\begin{aligned} \lambda _1&= -\delta \nonumber \\ \lambda _2&= \dfrac{\beta }{2} r^{*}L^{*}-\delta \nonumber \\ \lambda _3&= \beta r^{*}\big (L^{*}-\dfrac{s^{*}}{K}\big )-\delta \nonumber \\ \lambda _4&= -\delta . \end{aligned}$$
(3.9)

Hence, the eigenvalues associated with \(\mathbf p :=(0,0,0, {\mu }/{\delta })^{T}\) are \(\lambda _1 = -\delta ,\,\lambda _2={\beta } r^{*}L^{*}/2-\delta =-\varGamma /(2\delta ^2 K)-\delta /2,\,\lambda _3=\beta r^{*}L^{*}-\delta =-\varGamma /(\delta ^2 K)\) and \(\lambda _4 =-\delta \). Clearly, \(\lambda _{1},\lambda _{4}<0\). Thus, the stability of \(p\) will be determined by \(\lambda _{2}\) and \(\lambda _{3}\). If \(\varGamma \ge 0\), then \(\lambda _2<\lambda _3 \le 0\) and \(p\) is locally stable. If \(\varGamma <0\), then \(\lambda _3>0\), and \(p\) is unstable.

Recall that if \(\varGamma <0\), the system (2.1) has two equilibria: \(\mathbf p \) and \(\mathbf q :=\Big (0,0,K\Big (1-\dfrac{\delta ^2}{\mu \beta }\Big )-\dfrac{\mu }{\delta },\dfrac{\mu }{\delta }\Big )^{T}.\) One can easily verify that the eigenvalues associated with \(q\) are \(\lambda _1 = -\delta ,\,\lambda _2=-{\delta }/2,\,\lambda _3=-\beta r^{*}s^{*}/K\) and \(\lambda _4 =-\delta \). These eigenvalues are all negative, and hence \(q\) is locally stable.

So, if \(\varGamma \ge 0,\,\mathbf p \) represents the elimination state (ES) of the system; otherwise, \(\varGamma <0\) and \(\mathbf q \) represents the ES.

3.1.3 A condition for the eradication strategy

Let

$$\begin{aligned}&(H1): \Delta \ge 0, \alpha >4, { \text{ and } } \mu /\delta \ge r_b^{+};\end{aligned}$$
(3.10)
$$\begin{aligned}&(H2): \Delta \ge 0, \alpha \le 4, { \text{ and } } \mu /\delta \ge r_c;\end{aligned}$$
(3.11)
$$\begin{aligned}&(H3): \Delta < 0. \end{aligned}$$
(3.12)

By Propositions 3.1 and 3.3, if one of three hypothesis (H1)–(H3) is valid, the TYC model will only have the equilibria that satisfy \(f^{*}=0\) when \(\mu >0\). In other words, (H1)–(H3) provides a sufficient condition for the eradication strategy to work. Altogether with the analysis from Sect. 3.1.2, we have the following result.

Theorem 3.1

Suppose \(\mu >0\). If one of three hypothesis (H1)–(H3) holds, the eradication strategy works. Moreover, if \(\varGamma <0\), the TYC model (2.1) has two equilibria: \(\mathbf p :=(0,0,0,{\mu }/{\delta })^{T}\) and \(\mathbf{{q}}:=\Big (0,0,K\Big (1-\dfrac{\delta ^2}{\mu \beta }\Big )-\dfrac{\mu }{\delta },\dfrac{\mu }{\delta }\Big )^{T}\), and \(\mathbf p \) is locally unstable whereas \(\mathbf q \) is locally stable; if \(\varGamma \ge 0\), then the system (2.1) has only one equilibrium \(\mathbf p \) and it is locally stable. In either case, the stable equilibrium represents the elimination state of the wild-type species.

3.2 The case \(\mu =0\)

3.2.1 Equilibrium analysis

According to Theorem 3.1, the continual injection of the sex-reversed supermales can eliminate the wild-type females from the population. However, it is not practical to keep the introduction constant for all time. So, a natural question is: what happens if the introduction of the trojan fish is stopped after some time, that is, \(\mu =0\)?

If \(\mu =0\), we can verify by direct computation that the equilibrium of model (2.1) is of the form

$$\begin{aligned} (f^{*}, m^{*}, 0,0)^T, \quad {\text{ with } } f^{*}=m^{*}. \end{aligned}$$
(3.13)

For simplicity, we write \(\phi ={16\delta }/{\beta K}\). Clearly, \(\phi >0\) since \(\beta , K\) and \(\delta \) are all assumed to be positive. Let \(f^{*}_{\pm }=\dfrac{K}{4}(1\pm \sqrt{1-\phi })\). If \( \phi <1\), the TYC model (2.1) has three distinct equilibria for which \(f^{*}=f^{*}_{+},\,f^{*}_{-}\) and \(0\), respectively. If \(\phi =1\), the model has two equilibria and \(f^{*}=\dfrac{K}{4}\) and \(0\), respectively. Otherwise if \(\phi >1\), the system has only one equilibrium and \(f^{*}=0\).

Evaluate the Jacobian matrix (3.7) at the equilibria. In the case \(\phi \le 1\), we find that the corresponding characteristic equation is given by

$$\begin{aligned} \big (\lambda +\delta \big )^3\Big (\lambda -(2\gamma -\delta )\Big )=0, \end{aligned}$$
(3.14)

where \(\gamma =0\), or \(\gamma =\gamma _{\pm }:=\dfrac{\beta }{2}f^{*}_{\pm }\Big (1-\dfrac{3 f^{*}_{\pm }}{K}\Big )\). The associated eigenvalues are \(\lambda _i=-\delta <0\), for \(i=1,2,3\), and \(\lambda _4=-\delta ,\,2\gamma _{-}-\delta \) or \(2\gamma _{+}-\delta \). Therefore, the sign of \(\lambda _4\) determines the local stability of the equilibrium. In particular, at \((0,0,0,0)^T,\,\gamma =0\) and hence \(\lambda _i=-\delta <0\) for all \(1\le i\le 4\).

In addition, it follows from direct calculation that

$$\begin{aligned} 2\gamma _{\pm }-\delta =-\dfrac{2\delta }{\phi }\Big (1-\phi \pm \sqrt{1-\phi }\Big ). \end{aligned}$$
(3.15)

Then \(\phi \le 1\) yields \(2\gamma _{+}-\delta <0\) and \(2\gamma _{-}-\delta >0\). It demonstrates that the equilibrium \((0,0, 0,0)^T\) (which represents the elimination state) and \((f^{*}_{+}, f^{*}_{+}, 0,0)^T\) are locally stable (which represents the recovery state), whereas \((f^{*}_{-}, f^{*}_{-}, 0,0)^T\) is locally unstable, and is a saddle.

4 The Allee effect

The (component) Allee effect is a positive relationship between any measurable component of individual fitness and population size (Odum and Allee 1954; Stephens and Sutherlan 1999). Population-dynamic consequences of the Allee effect are of primary importance in conservation biology and other fields of ecology.

Due to the difficulty of finding mates at low population sizes, we introduce the Allee effect into the mathematical model of the TYC eradication strategy. A reasonable model (2.1) with the inclusion of an Allee effect takes the form:

$$\begin{aligned} \dfrac{df}{dt}&= \dfrac{1}{2} f m \bigg (\dfrac{f}{f_{0}}-1\bigg )\beta L-\delta f,\nonumber \\ \dfrac{dm}{dt}&= \Bigg (\dfrac{1}{2} f m \bigg (\dfrac{f}{f_{0}}-1\bigg )+ \dfrac{1}{2} rm\bigg (\dfrac{r}{r_{0}}-1\bigg ) + f s \bigg (\dfrac{f}{f_{0}}-1\bigg )\Bigg ) \beta L-\delta m,\nonumber \\ \dfrac{ds}{dt}&= \Big (\dfrac{1}{2} r m+ rs \Big ) \bigg (\dfrac{r}{r_{0}}-1\bigg ) \beta L-\delta s,\nonumber \\ \dfrac{dr}{dt}&= \mu -\delta r,\nonumber \\ L&= 1-\dfrac{f+m+s+r}{K}, \end{aligned}$$
(4.1)

where \(f_{0}\) (resp. \(r_{0}\)) is a critical value of \(f\) fish (resp. \(r\) fish), which is used to characterize the minimal group size to find mates, rear offspring, search for food and/or fend off attacks from predators. Mathematically, we assume that \(f_{0}\ll K,\) and \(r_{0}=f_{0}\). We denote this model (4.1) by ATYC model. Here our use of the cubic form for incorporating an Allee effect is for illustrative purposes only in the same spirit as its use in (Lewis and Kareiva 1993), and in the classical KPP equation (Kolmogorov et al. 1937).

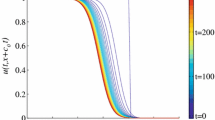
The eradication strategy works in the way that the wild-type female population can be eliminated by introducing the trojan fish. We have seen from the results in Sect. 3.2 that the wild-type fish will either go extinct or recover if the injection of the trojan fish is removed. Now the question is when would be the optimal termination time for such a removal? Here, by the “optimal termination time”, we mean the minimal time that is required to switch off the injection of the trojan fish so that the wild-type fish species won’t be able to recover thereafter. Let \({\tau }_{0}\) be the optimal termination time. Assume \(\mu =\mu _{0}\) if \(t\le t_{0}\) and \(\mu =0\) otherwise. The top panel in Fig. 2 illustrates that, in the original TYC model (2.1), the introduction of the trojan fish has to last until the number of the wild-type females, \(f\), is extremely low to guarantee that the wild-type fish will not recover. In this case, \({\tau }_{0}\approx 58\) (time unit), and \(f({\tau }_{0})<1\), which indeed provides no information for biological implementation. The middle (resp. the bottom) panel in Fig. 2 displays the associated results for the ATYC models with \(f_{0}=0.01K\) (resp. \(f_{0}=0.02K\)). Specifically, if \(f_{0}=0.01K,\,{\tau }_{0}\approx 34\) and \(f({\tau }_{0})\approx 21\) (which is about \(0.07 K\)); if \(f_{0}=0.02 K,\,{\tau }_{0}\approx 31\) and \(f({\tau }_{0})\approx 30\) (which is about \(0.1 K\)). Therefore, it indicates that: (1) the number of the wild-type female fish at the optimal termination time \({\tau }_{0}\) needs not be very low for the ATYC model; (2) the remaining trojan fish are sufficient to eliminate the wild-type females from the population after \({\tau }_{0}\).

Fig. 2
figure 2

The Allee effect is illustrated by comparing the solutions of the TYC model and those of ATYC model I. The top panel (resp. the middle and the bottom panels) shows the solutions of TYC model (2.1) (resp. the ATYC model (4.1) with \(f_{0}=3\) and \(f_{0}=6\)) at different termination time of \(t_{0}\). Here \(\mu =20\) if \(t\le t_{0}\), and \(\mu =0\) if \(t>t_{0}\). \(\beta =0.1,\,\delta =0.1\) and \(K=300\) (color figure online)

Full size image

5 The basin of attraction of the extinction state of a wild-type species when \(\mu =0\)

5.1 The reduced two-dimensional TYC model

The equilibrium analysis in Sect. 3.2.1 shows that both \(r\) and \(s\) would exponentially decay to \(0\) if \(\mu =0\). If \(r=s=0\) in the original model, (2.1) gives a reduced two-dimensional system as follows:

$$\begin{aligned} \dfrac{df}{dt}&= \dfrac{1}{2} f m \beta \Big (1-\dfrac{f+m}{K}\Big )-\delta f,\nonumber \\ \dfrac{dm}{dt}&= \dfrac{1}{2} f m \beta \Big (1-\dfrac{f+m}{K}\Big )-\delta m. \end{aligned}$$
(5.1)

Nondimensionalize model (5.1). Let \(x_{1}={f}/{K},\,x_2={m}/{K}\) and \(\tau =\delta t\). Recall that \(\alpha = \beta K/(2\delta )\). We get

$$\begin{aligned} \dfrac{dx_{1}}{d{\tau }}&= \alpha x_{1} x_2 (1-x_{1}-x_2)- x_{1},\nonumber \\ \dfrac{dx_2}{d{\tau }}&= \alpha x_{1} x_2 (1-x_{1}-x_2)-x_2. \end{aligned}$$
(5.2)

It can be seen from the bifurcation diagram for model (5.2) which is displayed in Fig. 3, if \(\alpha <8\) (i.e., \(\phi =16\delta /(\beta K)=8/\alpha >1\)), there is only one stable equilibrium. If \(\alpha =8\) (i.e., \(\phi =1\)), there are two equilibria: one is stable and the other one is unstable. If \(\alpha >8\) (i.e., \(\phi <1\)), there are three equilibria: one is unstable and the other two are stable. Focus on the most interesting case where \(\alpha >8\). One can verify that the three equilibria are: \(\mathbf p _0=(0,0),\,\mathbf{p _u}= ((1-\sqrt{1-\phi })/4, (1-\sqrt{1-\phi })/4),\) and \(\mathbf{p _s}=((1+\sqrt{1-\phi })/4, (1+\sqrt{1-\phi })/4)\). In particular, \(\mathbf p _0\) represents the ES, and \(\mathbf p _s\) represents the recovery state (RS). Let \((x_{1}^{*}, x_{2}^{*})\) denote the equilibrium of (5.2). Write \(\eta =\alpha x_{1}^{*}(1-3 x_{1}^{*})\). The eigenvalues of the system (5.2) are given by \(\lambda _1=2\eta -1\) and \(\lambda _2=-1\). One can verify that \(\mathbf p _0\) and \(\mathbf{p _s}\) are locally stable, whereas \(\mathbf{p _u}\) is a saddle.

Fig. 3
figure 3

Bifurcation diagram for the reduced two-dimensional model (5.2). The stable equilibrium and the unstable equilibrium are displayed by the solid curve and the dash-dot curve, respectively

Full size image

To study the basin of attraction for the ES, we analyze the dynamics of (5.2) at the saddle \(\mathbf p _u\). Let

$$\begin{aligned} \mathbf R _{\theta }= \left[ \begin{array}{ll} \cos (\theta )&{}\quad -\sin (\theta )\\ \sin (\theta ) &{}\quad \cos (\theta ) \end{array}\right] \end{aligned}$$
(5.3)

denote the rotation matrix. Consider the coordinate transformation

$$\begin{aligned} \left( \begin{array}{l} \varDelta {x_{1}} \\ \varDelta {x_2} \end{array}\right) = \mathbf R _{\pi /4} \left( \begin{array}{l} U\\ S \end{array}\right) , \end{aligned}$$
(5.4)

for which \(\varDelta x_{1}=x_{1}-x_{1}^{*}\) and \(\varDelta x_2 =x_2-x_2^{*}\). This yields

$$\begin{aligned} \dfrac{d}{dt} \left( \begin{array}{l} U\\ S \end{array}\right) = \left( \begin{array}{ll} \lambda _1 &{} 0\\ 0&{} \lambda _2 \end{array}\right) \left( \begin{array}{l} U\\ S \end{array}\right) + \left( \begin{array}{l} F(U,S)\\ 0 \end{array}\right) , \end{aligned}$$
(5.5)

where

$$\begin{aligned} F(U,S)=-\sqrt{2}\alpha x^{*}(U^2+S^2)+\alpha (1-4 x^{*})(U^2-S^2)/\sqrt{2}-\alpha (U^2-S^2)U.\nonumber \\ \end{aligned}$$
(5.6)

We now look for the curve on the \((U,S)\) phase plane such that it forms the separatrix between the basis of attraction for the ES and that for the RS. The separatrix indeed is the stable manifold of the origin \((U,S)^T=(0,0)^T\). Suppose such a curve exists. Then it has to be of the form \(U=U(S)=Sh(S)\) with \(h(0)=0\), because \(U(0)=U^{\prime }(0)=0\). By the invariant property on this curve, (5.5) yields

$$\begin{aligned} \lambda _2 S(h(S)+Sh^{\prime }(S)) = \lambda _1 Sh(S)+F(Sh(S), S). \end{aligned}$$
(5.7)

In view of Eq. (5.7) and \(h(0)=0\), we have

$$\begin{aligned} h(S)=\dfrac{1}{\lambda _2}S^{-n}\int \limits _0^{S} \xi ^{n-2} F(\xi h(\xi ), \xi )d\xi , \end{aligned}$$
(5.8)

where \(n=1-{\lambda _1}/{\lambda _2}\). It is clear that \(n>1\) because \(\lambda _1>0>\lambda _2\). Substitute \(\lambda _1=2\eta -1\) and \(\lambda _2=-1\) into the expression of \(n\). We get \(n=2\eta \). It then follows from the definition of \(F(U,S)\) in (5.6) that

$$\begin{aligned} F(U,S)=c_{20}U^2+c_{02}S^2+c_{30}U^3+c_{12}US^2, \end{aligned}$$
(5.9)

for which \(c_{20}=\alpha (1-6x_{1}^{*})/\sqrt{2},\,c_{02}= \alpha (-1+2x_{1}^{*})/\sqrt{2},\,c_{30}=-\alpha \) and \(c_{12}=\alpha \). Substitute (5.9) and \(\lambda _2=-1\) into (5.8). We have

$$\begin{aligned} h(S) = -S\int \limits _0^{1}\theta ^n\big (c_{20}(h(S\theta ))^2+c_{02}+c_{30}S\theta (h(S\theta ))^3+c_{12}S\theta h(S\theta )\big )d\theta .\nonumber \\ \end{aligned}$$
(5.10)

In general, (5.10) has no closed-form analytical solution. We have to rely on the numerical method to evaluate it (Atkinson 1992, 1997). Let \(W^s(\mathbf p _u)\) denote the stable manifold at \(\mathbf p _u\). Figure 4 shows \(W^s(\mathbf p _u)\) with different values of the parameter \(\alpha \). If the initial position \((x_1(0),x_2(0))^T\) is below \(W^s(\mathbf p _u)\), the solution will converges to \(\mathbf p _0\) (which is illustrated by the directed solid curves in Fig. 4). This demonstrates the extinction of the invasive species. Otherwise, if the initial \((x_1(0),x_2(0))^T\) is above \(W^s(\mathbf p _u)\), the solution will converge to \(\mathbf p _s\) (which is illustrated by the directed dashed curves in Fig. 4). This shows the recovery of the invasive species. Therefore, \(W^s(\mathbf p _u)\) serves as a separatrix that separates the extinction from the recovery. Besides, if \(\alpha \) increases, Fig. 4 shows that the separatrix \(W^s(\mathbf p _u)\) is moving towards an L-shaped curve which comprises two segments of axes in the first quadrant restricted to the unit square \([0,1]\times [0,1]\). Thus, the results show that: (1) the basin of attraction of the ES expands as \(\alpha \) goes down to the bifurcation point \(8\); (2) the basin of attraction of the ES dramatically decreases as \(\alpha \) goes up and becomes unbounded. Moreover, if \(\alpha \gg 8\), the wild-type invasive fish can always be established, as along as their initial population is not very low.

Fig. 4
figure 4

The separatrix \(W^s(\mathbf p _u)\) of the extinction and the recovery of the invasive fish species \(f\), which are displayed in bold solid curves. The dashed (resp. dotted) curve is the nullcline for \(x_{1}^{\prime }(t)=0\) (resp. \(x_{2}^{\prime }(t)=0\)). The solid and dashed curves are trial solutions of (5.2). The dashed ones converge to the recovery equilibrium \(\mathbf p _s\), whereas the solid ones converge to the extinction equilibrium \(\mathbf p _0\)

Full size image

5.2 The full TYC model (2.1) when \(\mu =0\)

Returning to the full model (2.1), it is natural to ask whether the wild-type invasive fish species will die off or recover after the removal of the introduction of sex-reversed supermales, that is, \(\mu =0\).

Let \(x_1=f/K,\,x_2=m/K,\,x_3=s/K\) and \(x_4=r/K\). Rescale time \(\tau =\delta t\). Nondimensionalize the TYC model (2.1) with \(\mu =0\). We get

$$\begin{aligned} \dfrac{dx_1}{d\tau }&= \alpha x_1 x_2 \hat{L}-x_1,\nonumber \\ \dfrac{dx_2}{d\tau }&= \alpha (x_1x_2+x_2 x_4+2 x_1 x_3) \hat{L} -x_2,\nonumber \\ \dfrac{dx_3}{d\tau }&= \alpha (x_2 x_4 + 2 x_3 x_4) \hat{L}-x_3,\nonumber \\ \dfrac{dx_4}{d\tau }&= -x_4, \end{aligned}$$
(5.11)

where \(\hat{L}=1-\sum _{i=1}^4\, x_i\). Define \(\mathbf X = (x_1,x_2,x_3,x_4)^4\) and \(\mathbf F \) to be vector of the right hand sides of Eq. (5.11). Then Eq. (5.11) can be written as:

$$\begin{aligned} \dfrac{d\mathbf X }{d\tau }=\mathbf F (\mathbf X ). \end{aligned}$$
(5.12)

In view of the results in Sect. 3.2, the equilibrium of (5.11) is of the form \(p^{*}=(x^{*},x^{*},0,0)^T\), and the associated Jacobian matrix is given by

$$\begin{aligned} \mathbf M =D\mathbf F (p^{*})= \left[ \begin{array}{llll} \eta -1&{}\quad \eta &{}\quad -B &{}\quad -B\\ \eta &{}\quad \eta -1&{}\quad 2A-B &{}\quad \eta \\ 0&{}\quad 0 &{}\quad -1 &{}\quad A\\ 0&{}\quad 0&{}\quad 0&{}\quad -1 \end{array}\right] , \end{aligned}$$
(5.13)

where \(\eta = A-B\) with \(A=\alpha x^{*}\hat{L}^{*},\,B=\alpha \, (x^{*})^2\) and \(\hat{L}^{*}=1- 2 x^{*}\). If \(x^{*}=0\), then \(\mathbf M =-\mathbf I _4\) where \(\mathbf I _4\) represents the \(4\times 4\) identity matrix. If \(x^{*}\ne 0\), then \(\eta =A-B=\alpha x^{*}(1-3x^{*})> 0\). Let

$$\begin{aligned} \mathbf T = \left[ \begin{array}{llll} {T}_{11}&{}\quad {T}_{12}&{}\quad {T}_{13}&{}\quad -{T}_{23}\\ -{T}_{11}&{}\quad {T}_{22}&{}\quad {T}_{23} &{}\quad -{T}_{23} \\ 0&{}\quad {T}_{32} &{}\quad {T}_{33} &{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0 \end{array}\right] , \end{aligned}$$

where \({T}_{11}=-A^2,\,{T}_{12}={(2AB-3 A^2)}/{(2\eta )},\,{T}_{13}=(-7A^2+8AB-2B^2+2\eta B)/{(4\eta ^2)},\,{T}_{22}={A^2}/{(2\eta )},\,{T}_{23}={A^2}/{(4 \eta ^2)},\,{T}_{33}={(2A-B-\eta )}/{(2 \eta )}\), and \({T}_{32}=A\). Then by the coordinate transformation \(\mathbf X =p+\mathbf T \mathbf Y \), Eq. (5.12) yields

$$\begin{aligned} \dfrac{d\mathbf Y }{dt}= \mathbf{J }\mathbf Y + \mathbf G (\mathbf Y ), \end{aligned}$$
(5.14)

where \(\mathbf J \) is the Jordan canonical form of \(M\) with

$$\begin{aligned} \mathbf{J }= \left[ \begin{array}{llll} -1&{}\quad 1&{}\quad 0 &{}\quad 0\\ 0&{}\quad -1&{}\quad 1 &{}\quad 0 \\ 0&{}\quad 0 &{}\quad -1 &{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 2\eta -1 \end{array}\right] , \end{aligned}$$

and \(\mathbf G (\mathbf Y )=\mathbf{T }^{-1}(\mathbf F (p+\mathbf T \mathbf Y )-\mathbf M \mathbf T \mathbf Y )\).

Consider \(0<\phi <1\). At \(\mathbf{p _u}\), the eigenvalue \(\sigma _{4}:=2\eta -1>0\). Hence the Jordan form (5.13) indicates that \(\mathbf p _u\) is hyperbolic of saddle type. Thus, there exists a solution flow of equation (5.14), \( \mathbf{\Psi }(t; {\xi }_1,{\xi }_2,{\xi }_3)\in C^1([0, \infty ), U)\), for some neighborhood \(U\subset \mathbb R ^3\), and \(\lim _{t\rightarrow \infty } \mathbf \Psi (t;{\xi }_1,{\xi }_2,{\xi }_3)=\text{0 }\). Specifically, for any \(\mathbf C =(c_1,c_2,c_3,0)^T\) with \((c_1,c_2,c_3)^T\in U,\,\mathbf \Psi (t, \cdot )\) is given by

$$\begin{aligned} \mathbf{\Psi }(\tau ;\mathbf C ) = \mathbf{\Phi }^s(\tau )\mathbf C +\int \limits _0^{\tau } \mathbf \Phi ^s(\tau -s)\mathbf G (\mathbf \Psi (s))ds -\int \limits _{\tau }^{\infty } \mathbf \Phi ^u(\tau -s)\mathbf G (\mathbf \Psi (s))ds, \end{aligned}$$

where

$$\begin{aligned} \mathbf \Phi ^s(\tau )= \left[ \begin{array}{llll} e^{-\tau }&{}\quad \tau e^{-\tau }&{}\quad \frac{1}{2}\tau ^2 e^{-\tau } &{}\quad 0\\ 0&{}\quad e^{-\tau }&{}\quad \tau e^{-\tau } &{}\quad 0 \\ 0&{}\quad 0 &{}\quad e^{-\tau } &{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{array}\right] , \end{aligned}$$

and

$$\begin{aligned} \mathbf \Phi ^u(\tau )= \left[ \begin{array}{llll} 0&{}\quad 0&{}\quad 0 &{}\quad 0\\ 0&{}\quad 0&{}\quad 0 &{}\quad 0 \\ .eps 0&{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad e^{\sigma _{4} \tau } \end{array}\right] . \end{aligned}$$

Then system (5.14) processes a \(3\)-dimensional local stable manifold at the origin \(\text{0 }\),

$$\begin{aligned} W^s_{loc}(\text{0 })=\{({\xi }_1,{\xi }_2,{\xi }_3,{\xi }_4)^T: {\xi }_4={\Psi }_4(0; {\xi }_1,{\xi }_2,{\xi }_3), ({\xi }_1,{\xi }_2,{\xi }_3)^T\in U\},\qquad \end{aligned}$$
(5.15)

for which \(\mathbf \Psi =(\Psi _1, \Psi _2,\Psi _3,\Psi _4)^T\).

Let \(n=(n_1,n_2, n_3,n_4)^T\) with \(n_1=n_2=1,\,n_3=-(T_{12}+T_{22})/T_{32}\) and \(n_4=\big (T_{33}(T_{12}+T_{22})-T_{32}(T_{13}+T_{23})\big )/T_{32}\), which denotes the normal vector of the local stable manifold at \(\mathbf p _u\). Let \(t_{0}\) denote the time at which the introduction of the sex-reversed supermales \(r\) is switched off. Since \(\mathbf p _{u}\) is hyperbolic of saddle type, there exists a neighborhood \(\mathbf U _{0}\) such that \(W^s_{loc}(\text{0 })\) is well-defined and the following results hold: (1) if \(\mathbf X (t_{0})\) satisfies \(\mathbf{T }^{-1}(\mathbf X (t_{0})-\mathbf p _u)\in \mathbf U _{0} \) and \(\mathbf{T }^{-1}(\mathbf X (t_{0})-\mathbf p _u)\cdot n>0\), the solution of Eq. (5.11) will converge to \(\mathbf p _s\), which implies that the invasive fish species \(f\) and \(m\) will recover after the removal of \(r\) (see the red curves in Fig. 5); (2) whereas if \(\mathbf{T }^{-1}(\mathbf X (t_{0})-\mathbf p _u)\in \mathbf U _{0} \) and \(\mathbf{T }^{-1}(\mathbf X (0)-\mathbf p _u)\cdot n<0\), the solution will approach \(\mathbf p _0\), which indicates that \(f\) and \(m\) will go extinct after the trojan introduction is stopped (see the blue curves in Fig. 5).

Fig. 5
figure 5

Projection of some trajectories of the TYC model (5.11) onto the \(x_{1}x_{2}\) plane. The red (resp. blue) curves represents recovery (resp. extinction) of the wild-type invasive species. The associated initials of these trajectories are in a close neighborhood of the saddle fixed point \(\mathbf p _{u}\). The black curves show the solutions of (5.11) that are very close to the projection of the separatrix of recovery and extinction onto the \(x_{1}x_{2}\) plane. Here \(x_{3}=1/300\) and \(x_{4}=10/300\) (color figure online)

Full size image

Therefore, by (5.11), whether the wild-type species will die off after the injection of trojan females is stopped depends on the value of the parameter \(\alpha \) and the initial state of the trajectories. Specifically, if \(\alpha \) is a constant, the stable manifold of \(\mathbf p _{u}\) provides a separatrix of extinction and recovery. If the initial state is identical, increasing \(\alpha \) will result in the basin of the attraction of the extinction shrinking whereas that of the recovery expanding (see Fig. 5).

5.3 The reduced 2-dimensional ATYC model

We consider the case when \(r=s=0\) in the full ATYC model (4.1). It yields a reduced two-dimensional system

$$\begin{aligned} \dfrac{df}{dt}&= \dfrac{1}{2} f m \beta L \left( \dfrac{f}{f_{0}}-1\right) -\delta f,\nonumber \\ \dfrac{dm}{dt}&= \dfrac{1}{2} f m \beta L \left( \dfrac{f}{f_{0}}-1\right) -\delta m. \end{aligned}$$
(5.16)

Let \(x_{1}={f}/{K},\,x_2={m}/{K},\,x_{0}=f_{0}/K\) and \(\tau =\delta t\). Nondimensionalizing model (5.16) gives

$$\begin{aligned} \dfrac{dx_{1}}{d{\tau }}&= \alpha x_{1} x_2 (1-x_{1}-x_2)(x_{1}/x_{0}-1)- x_{1},\nonumber \\ \dfrac{dx_2}{d{\tau }}&= \alpha x_{1} x_2 (1-x_{1}-x_2)(x_{1}/x_{0}-1)-x_2. \end{aligned}$$
(5.17)

Bifurcation diagrams for the reduced model (5.17) are displayed in Fig. 6. Figure 6a shows the steady-state behavior of \(x_{1}\) (which is the dimensionless counterpart of \(f\)) as a function of \(\alpha \) when \(x_{0}\) is \(0.05\). Note that the stability of the system (5.17) changes at the limit point, \(LP\). There is a unique stable equilibrium point \(\mathbf p _{0}=(0,0)^{T}\) if \(\alpha <LP\) (\(\alpha \approx 1.6\) as \(x_{0}=0.05\)). At \(\alpha =LP\), there are two equilibria and only the lower branch is stable. If \(\alpha >LP\), there will be three equilibria: \(\mathbf p _{0}\) (the lower branch), \(\mathbf p _{u}\) (the middle branch) and \(\mathbf p _{s}\) (the top branch), for which \(\mathbf p _{u}\) is unstable and indeed a saddle, and both \(\mathbf p _{0}\) (representing the ES) and \(\mathbf p _{s}\) (repenting the RS) are stable. Thus, a saddle-node bifurcation occurs at \(LP\). If \(x_{0}\) varies, Fig. 6 b displays a two-parameter bifurcation, which illustrates how \(\alpha \) changes as \(x_{0}\) varies at the LP. In particular, it shows that, at the LP, if \(x_0\le 0.1\), there is a nearly linear relationship between \(\alpha \) and \(x_0\); if \(x_0>0.1\), this relationship becomes highly nonlinear.

Fig. 6
figure 6

Bifurcation diagram for the reduced two-dimensional model (5.17). a \(x_{1}\) as a function of \(\alpha \) with \(x_{0}=0.05\). The stable equilibrium (resp. unstable equilibrium) is displayed by the solid curve (resp. the dash-dot curve). b Two-parameter bifurcation showing \(\alpha \) as a unction of \(x_{0}\) at the limit point (LP)

Full size image

Consider the case \(\alpha >LP\). Let \(W^s(\mathbf p _u)\) denote the stable manifold at \(\mathbf p _{u}\). Figure 7 shows the phase plane of (5.2) with different values of \(\alpha \) as \(x_{0}=0.05\). If the initial position \((x_1(0),x_2(0))^T\) is below \(W^s(\mathbf p _u)\), the solution will approach \(\mathbf p _0\) (which is illustrated by the directed solid curves in Fig. 7). This demonstrates extinction of the invasive species. Otherwise, if the initial \((x_1(0),x_2(0))^T\) is above \(W^s(\mathbf p _u)\), the solution will converge to \(\mathbf p _s\) (which is illustrated by the directed dash-dot curves in Fig. 7). This shows the recovery of the invasive fish species. Thus, \(W^s(\mathbf p _u)\) serves as the separatrix that separates extinction from the recovery. Moreover, if \(\alpha \) increases, Fig. 7 shows that \(W^s(\mathbf p _u)\) is moving towards an L-shaped curve \(\{(x_{1},x_{2}): x_{1}=x_{0}, x_{2} =0\}\). The results indicate that: (1) the basin of attraction of the ES expands as \(\alpha \) goes down to the limit point \(LP\); (2) the basin of attraction of the ES dramatically diminishes as \(\alpha \) increases. However, compared to the reduced TYC model (5.2), if \(\alpha \gg LP\), the wild-type invasive fish can only be established if the initial female population size is above the critical value \(f_{0}\).

Fig. 7
figure 7

The separatrix \(W^s(\mathbf p _u)\) (the bold solid curves) of the extinction and the recovery of the invasive species by using ATYC model. The dash-dot (resp. dotted) curve shows the nullcline for \(x_{1}^{\prime }(t)=0\) (resp. \(x_{2}^{\prime }(t)=0\)). The directed solid (resp. dash-dot) curves are trial solutions, in which the dash-dot ones converge to the recovery equilibrium \(\mathbf p _s\), whereas the solid ones converge to the extinction equilibrium \(\mathbf p _0\)

Full size image

6 Turing instability

In this section, we study the possibility of a Turing (1952) instability for the TYC model generalized by incorporating diffusive spatial spread.

6.1 A reaction-diffusion model on a line

First, we consider a continuous region in the shape of a line by assuming that the density difference of each fish population at different position causes diffusion. Let \(\theta \in [0,1]\) denote the position variable on a line. Assume that \(\gamma _i>0 \) \((1\le i\le 4)\) is the diffusion constant of \(f,\,m,\,s\) and \(r\) fish species. Then the generalized system of (5.11) with inclusion of diffusive spatial spread takes the form:

$$\begin{aligned} \dfrac{\partial x_1}{\partial \tau }&= \alpha x_1 x_2 \hat{L}-x_1+\tilde{D_1}\dfrac{\partial ^{2} {x_1}}{\partial \theta ^{2}} ,\nonumber \\ \dfrac{\partial x_2}{\partial \tau }&= \alpha (x_1x_2+x_2 x_4+2 x_1 x_3) \hat{L} -x_2+\tilde{D_2}\dfrac{\partial ^{2} {x_2}}{\partial \theta ^{2}},\nonumber \\ \dfrac{\partial x_3}{\partial \tau }&= \alpha (x_2 x_4 + 2 x_3 x_4) \hat{L}-x_3+\tilde{D_3}\dfrac{\partial ^{2} {x_3} }{\partial \theta ^{2}} ,\nonumber \\ \dfrac{\partial x_4}{\partial \tau }&= \nu -x_4+\tilde{D_4}\dfrac{\partial ^{2} {x_4}}{\partial \theta ^{2}} , \end{aligned}$$
(6.1)

where \(\tilde{D_i}=\gamma _i/\delta \) for \( 1\le i\le 4\) and \(\nu =\mu /(\delta K)\). We linearize (6.1) at the steady state, \(\mathbf p :=(x_1^{*},x_3^{*},x_3^{*},x_4^{*})^T\), of the system (6.1) in the absence of diffusion. Set

$$\begin{aligned} x_i&=x_i^{*}+\delta x_i, \quad (i=1,2,3,4). \end{aligned}$$
(6.2)

Let \( \mathbf Z =(\delta {x_{1}}, \delta {x_{2}}, \delta {x_{3}}, \delta {x_{4}})^{T}\). The associated linearized system in vector form is given by

$$\begin{aligned} \dfrac{\partial \mathbf Z }{\partial \tau } = \mathbf M \mathbf Z +\tilde{\mathbf{D }}\dfrac{\partial ^{2} }{\partial \theta ^{2}} { \mathbf Z }, \end{aligned}$$
(6.3)

where \(\mathbf M \) is the Jacobian matrix of the associated ODE system evaluated at \(\mathbf p \), and

$$\begin{aligned} \tilde{\mathbf{D }}= \left[ \begin{array}{llll} \tilde{D_1}&{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \tilde{D_2}&{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \tilde{D_3}&{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \tilde{D_4} \end{array}\right] . \end{aligned}$$

Consider the eigenvalue problem

$$\begin{aligned} {\left\{ \begin{array}{ll} - \upsilon _{\theta \theta }(\theta )=\sigma \upsilon (\theta ), &{} \theta \in (0,1),\\ \upsilon _{\theta }(\theta )=0, &{} \theta =0,1. \end{array}\right. } \end{aligned}$$
(6.4)

One can easily verify that the eigenvalues \(\sigma _k=(k\pi )^2\ge 0\) and the corresponding eigenfunctions \(\upsilon _k(\theta )=\cos (k\pi \theta )\). We consider the ansatz

$$\begin{aligned} \delta x_i(t,\theta )=e^{\rho \tau }\upsilon (\theta )\xi _i, \quad (1\le i \le 4), \end{aligned}$$
(6.5)

where \(\upsilon \) is the solution of the eigenvalue problem (6.4), and \(\rho \) and \( \xi _i\) are constant. Substituting (6.5) into (6.3) yields

$$\begin{aligned} (\rho \mathbf I _4+\sigma \tilde{\mathbf{D }})\xi =\mathbf M \xi . \end{aligned}$$
(6.6)

We are interested in whether there exists \(\rho \) such that \(\mathrm{{Re}}(\rho )>0\).

First, we consider the case \(\mu =0\). Solve (6.6). We find that the associated eigenvalues are given by

$$\begin{aligned} \rho _1&= \eta -1-\sigma ( \tilde{D}_1+ \tilde{D}_2)/2+\sqrt{\eta ^2+(\sigma (\tilde{D}_1- \tilde{D}_2)/2)^2},\nonumber \\ \rho _2&= \eta -1-\sigma ( \tilde{D}_1+ \tilde{D}_2)/2-\sqrt{\eta ^2+(\sigma (\tilde{D}_1- \tilde{D}_2)/2)^2},\nonumber \\ \rho _3&= -(\sigma \tilde{D}_3+1),\nonumber \\ \rho _4&= -(\sigma \tilde{D}_4+1), \end{aligned}$$
(6.7)

where \(\eta \) is defined in (5.13).

Proposition 6.1

Suppose \(\mu =0\). Inclusion of diffusive spatial spread into model (5.11) will not produce a Turing instability.

Proof

Since \(\rho _2,\rho _3\) and \(\rho _4\) are all negative and have the same sign as the corresponding eigenvalue of \(M\), the only eigenvalue that could have a sign change is \(\rho _1\). Thus, it suffices to study the sign of \(\rho _{1}\).

If \(0<\phi <1\), then (5.11) has three equilibria: \(\mathbf p _{0}, \mathbf p _{u}\) and \(\mathbf p _{s}\), in which \(\mathbf p _0\) and \(\mathbf p _s\) are stable.

Case 1 \(\mathbf p =\mathbf p _{0}\), which represents the ES of (5.11). Then \(x^{*}=0\) and \(\eta =0\). Hence (6.7) yields

$$\begin{aligned} \rho _1&=-(\sigma \tilde{D}_1+1)<0. \end{aligned}$$

Case 2 \(\mathbf p =\mathbf p _{s}\), which corresponds to the RS of (5.11).

In this case, \(x^{*}=(1+\sqrt{1-\phi })/4\) and \(\eta =-\Big (1-\phi + \sqrt{1-\phi }\Big )/\phi +1/2\). Thus \(0<\phi <1\) implies \(\eta <1/2\). By \(2\eta -1<0\) and \(\eta -1<0\), we find that

$$\begin{aligned} \rho _1\rho _{2}&= \Big (\eta -1-\sigma ( \tilde{D}_1+ \tilde{D}_2)/2\Big )^2-\Big (\eta ^2+(\sigma (\tilde{D}_1- \tilde{D}_2)/2)^2\Big ),\\&= -(2\eta -1)+2\sigma \tilde{D}_1 \tilde{D}_2-\lambda (\eta -1)(\tilde{D}_1+ \tilde{D}_2)>0. \end{aligned}$$

Then \(\rho _2<0\), which implies that \(\rho _1<0\).

If \(\phi \ge 1\), (5.11) has a unique stable equilibrium \(\mathbf p _{0}\). By the analysis in the first case of \(0<\phi <1\), all the eigenvalues associated with \(\mathbf p _{0}\) will keep the same sign.

Therefore, inclusion of diffusive spatial spread will stabilize the system (5.11), and will not be able to produce a Turing instability. \(\square \)

Remark

In fact, if (i) \(\phi =1\) or (ii) \(0<\phi <1\) and \(-(2\eta -1)+2\sigma \tilde{D}_1 \tilde{D}_2-\sigma (\eta -1)(\tilde{D}_1+ \tilde{D}_2)>0\), then inclusion of diffusive spatial spread can even stablize the unstable steady-state solution of model (5.11).

Now consider the case \(\mu >0\). Define \(\hat{\lambda }_{1}=-1,\,\hat{\lambda }_{2}=\alpha x^{*}_{4}(1-x^{*}_{3}-x^{*}_{4})-1,\,\hat{\lambda }_{3}=2\alpha x^{*}_{4}(1-2x^{*}_{3}-x^{*}_{4})-1,\,\hat{\lambda }_{4}=-1\), and \(\hat{\varGamma }=\varGamma /\delta \).

Proposition 6.2

Suppose \(\mu >0\). Assume that one of three hypothesis (H1)–(H3) holds. Inclusion of diffusive spatial spread into model (5.11) does not produce a Turing instability.

Proof

If (H1)–(H3) hold, then by Theorem 3.1, the steady-state solution of (5.11) would take the form \((0,0,x^{*}_{3}, x^{*}_{4})^{T}.\) Moreover, if \(\hat{\varGamma }\ge 0\), (5.11) has a unique stable equilibrium \(\mathbf p :=(0,0,0,x^{*}_{4})^{T}.\) If \(\hat{\varGamma }<0\), (5.11) will have two equilibria \(\mathbf p \) and \(\mathbf q :=(0,0,x^{*}_{3},x^{*}_{4})^{T}\), for which \(\mathbf p \) is unstable and \(\mathbf q \) is locally stable. In both cases, by (6.6), we find that

$$\begin{aligned} \rho _i=\hat{\lambda }_{i}-\sigma \tilde{D}_{i}, \quad (i=1,2,3,4). \end{aligned}$$
(6.8)

Note that \(\{\hat{\lambda }_{i}:i=1,2,3,4\}\) is the spectrum of \(M\). For each \(1\le i\le 4\), at the stable fixed point, \(\hat{\lambda }_{i}<0\), and hence \(\rho _{i}<0\) by (6.8). So, no Turing instability would be able to be established at the stable equilibrium for both cases by adding diffusion into model (5.11). \(\square \)

6.2 A stepping-stone type model: reaction and migration in a circle

Fish populations migrate between regions. To study the effect of fish migration on the closed area, a “stepping-stone” type of model, which is continuous in time and discrete in state space, is developed as follows: (a) \(N\) colonies are assumed to be arranged on a circle, labeled by integers \(n=1,2,\cdots , N\) with \(f_n(t)\), \(m_n(t),\,s_n(t)\) and \(r_n(t)\) denoting the number of \(f,\,m,\,s\) and \(r\) fish in colony \(n\) at time \(t\), respectively. In particular \(n\) and \(mod(n,N)\) represent the same colony. (b) Each fish species is assumed to have a constant migration rate. Let \(\zeta _1,\zeta _2,\zeta _3\) and \(\zeta _4\) denote the migration rates for fish species \(f,\,m,\,s\) and \(r\), respectively. (c) The individuals of each species are assumed to move between adjacent colonies. Specifically, the overall migration into colony \(n\) is assumed to come from the two nearest neighbors \(n-1\) and \(n\) colonies; whereas the overall migration out of colony \(n\) is assumed to go to two nearest neighbors \(n-1\) and \(n+1\) colonies. Taking \(f_n\) as an example, the rate at which \(f_n\) increase due to the migration from nearest neighbors colony \(n-1\) and colony \(n+1\) is then \(\zeta _1 (f_{n-1}+f_{n+1})\); the rate at which \(f_n\) decreases due to the migration to colonies \(n-1\) and \(n+1\) is then \(\zeta _1 f_n+\zeta _1 f_n\), where the first term (resp. the second term) describes the migration from colony \(n\) to colony \(n-1\) (resp. colony \(n+1\)). Thus, the model with the inclusion of fish migration can be written as:

$$\begin{aligned} \dfrac{df_n}{dt}&= \dfrac{1}{2} f_n m_n \beta L_{n}-\delta f_n+\zeta _1 \left( f_{n-1}-2f_n+f_{n+1}\right) ,\nonumber \\ \dfrac{dm_n}{dt}&= \left( \dfrac{1}{2} f_n m_n + \dfrac{1}{2} r_n m_n + f_n s_n\right) \beta L_{n}-\delta m_n \nonumber \\&+ \,\zeta _2\left( m_{n-1}-2m_n+m_{n+1}\right) ,\nonumber \\ \dfrac{ds_n}{dt}&= \left( \dfrac{1}{2} r_n m_n + r_n s_n \right) \beta L_{n}-\delta s_n ++\zeta _3 \left( s_{n-1}-2s_n+s_{n+1}\right) ,\nonumber \\ \dfrac{dr_n}{dt}&= \mu -\delta r_n+\zeta _4 \left( r_{n-1}-2r_n+r_{n+1}\right) , \end{aligned}$$
(6.9)

where

$$\begin{aligned} L_{n}=1-\Big ({f_n+m_n+s_n+r_n}\Big ) \Big /K. \end{aligned}$$

Let \(\alpha =\beta K/(2 \delta ),\,\tau =\delta t,\,\nu =\mu /(\delta K)\) and \(\sigma _i=\zeta _i/\delta \) (for \(i=1,2,3,4\)). Write \(x_1^n=f_n/K,\,x_2^n=m_n/K,\,x_3^n=s_n/K\) and \(x_4^n=r_n/K\). Non-dimensionalization of (6.9) yields

$$\begin{aligned} \dfrac{dx_1^n}{d\tau }&= \alpha x_1^n x_2^n L_{n}-x_1^n+\sigma _1 \Big (x_1^{n-1}-2x_1^n+x_1^{n+1}\Big ),\nonumber \\ \dfrac{dx_2^n}{d\tau }&= \alpha \Big (x_1^n x_2^n + x_4^n x_2^n + 2 x_1^n x_3^n\Big ) L_{n}- x_2^n +\sigma _2 \Big (x_2^{n-1}-2x_2^n+x_2^{n+1}\Big ),\nonumber \\ \dfrac{dx_3^n}{d\tau }&= \alpha \Big ( x_4^n x_2^n + 2 x_4^n x_3^n \Big ) L_{n}-x_3^n +\sigma _3 \Big (x_3^{n-1}-2x_3^n+x_3^{n+1}\Big ),\nonumber \\ \dfrac{dx_4^n}{d\tau }&= \nu -x_4^n+\sigma _4 \Big (x_4^{n-1}-2x_4^n+x_4^{n+1}\Big ), \end{aligned}$$
(6.10)

where

$$\begin{aligned} L_{n}=1-\Big ({x_1^n+x_2^n+x_3^n+x_4^n}\Big ). \end{aligned}$$

If the introduction of \(r\) fish is removed, \(\mu =0\) and hence \(\nu =0\). In this case, let \(\mathbf F _n(\mathbf X )\) denote the right hand side of the system (6.10) without migration terms. Solve \(\mathbf F _n(\mathbf p )=0\). We find the equilibrium \(\mathbf p \) of each colony given by \((x^{*},x^{*},0,0)^T\).

If the system is not far away from the equilibrium, we consider small perturbations \((\delta x_1^n, \delta x_2^n, \delta x_3^n, \delta x_4^n)^T\) of the equilibrium

$$\begin{aligned} x_j^n&= x^{*}+\delta x_j^n, \quad (j=1,2),\end{aligned}$$
(6.11)
$$\begin{aligned} x_j^n&= \delta x_j^n, \quad (j=3,4). \end{aligned}$$
(6.12)

Under this linear approximation, the Eq. (6.10) can be rewritten as

$$\begin{aligned} \dfrac{d}{d\tau }\delta x_j^n&= \sum _{k=1}^{4}M_{jk}\delta x_k^n+\sigma _j \Big (\delta x_j^{n-1}-2\delta x_j^n+\delta x_j^{n+1}\Big ), \end{aligned}$$
(6.13)

for \(1\le j \le 4\). Here \(\mathbf M =(M_{jk})=D_{X_n}\mathbf F _n\Big |_\mathbf{X _n=p}\) with \(\mathbf X _n=(x_1^n,x_2^n,x_3^n,x_4^n)^T\).

To solve (6.13) in this case, one can use discrete Fourier transformation

$$\begin{aligned} \delta x_j^n = \dfrac{1}{N}\sum _{r=1}^{N} u_j^r \exp {\Big (2\pi r i \frac{n}{N}\Big )}, \end{aligned}$$
(6.14)

where

$$\begin{aligned} u_j^r = \sum _{n=1}^{N} \delta x_j^n \exp {\Big (-2\pi n i\frac{r}{N}\Big )},\quad \mathrm{{ and }}\,\, i=\sqrt{-1}. \end{aligned}$$

Let \(D_j^r=4\sigma _i\sin ^2(\omega _r)\) with \(\omega _r=\pi r/N\). Substitue (6.14) into Eq. (6.13). We find that

$$\begin{aligned} \dfrac{du_j^r}{d\tau } = \sum _{k=1}^{4}M_{jk} u_k^r-D_j^{r} u_j^r,\quad 1\le j \le 4, 1\le r \le N. \end{aligned}$$
(6.15)

Given \(1\le r\le N\), the characteristic equation of (6.15) is given by

$$\begin{aligned} \det (\lambda \mathbf I _4-(\mathbf M -\mathbf D ^r))=0, \end{aligned}$$
(6.16)

with

$$\begin{aligned} \mathbf D ^r= \left[ \begin{array}{llll} D_1^r&{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad D_2^r&{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad D_3^r&{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad D_4^r \end{array}\right] . \end{aligned}$$

Solve (6.16).

$$\begin{aligned} \lambda _1^r&= \eta -1-( {D_1^{r}}+ {D_2^{r}})/2+\sqrt{\eta ^2+\big (({D_1^{r}}- {D_2^{r}}\big )/2)^2},\nonumber \\ \lambda _2^r&= \eta -1-( {D_1^{r}}+ {D_2^{r}})/2-\sqrt{\eta ^2+(\big ({D_1^{r}}- {D_2^{r}}\big )/2)^2},\nonumber \\ \lambda _3^r&= -( {D_3^{r}}+1),\nonumber \\ \lambda _4^r&= -( {D_4^{r}}+1), \end{aligned}$$

with \(\eta = \alpha x^{*}(1-3 x^{*})\).

Compared to the continuous case in Sect. 6.1, the arguments are similar and the associated results on the existence of Turing instability are the same. So the details are omitted for the discrete case.

7 Conclusion and discussion

The analysis presented here is intended to inform details of the behavior of certain limiting mathematical systems modeling the TYC strategy for the biological control of some very specific invasive species. In this work, we study questions that haven’t been addressed in (Gutierrez and Teem 2006; Gutierrez 2005; Parshad and Gutierrez 2010). Specifically, we study the equilibrium and the stability of model (2.1).We also address the natural question of how long must the Trojan females be supplied in order to cause the species to die out. Thus, we investigate what will happen if this injection is turned off, after some time. We theoretically study this situation through bifurcation analysis. We find that the wide-type invasive population can either go extinct or recover. Moreover, extinction and recovery are essentially modulated by a parameter \(\alpha =\beta K/(2\delta )\), which is defined by the ratio of the the overall birth rate in terms of the maximal capacity of the ecosystem to two times the per capita death rate. If \(\alpha \) is below the bifurcation value, only extinction can take place; if \(\alpha \) is above the bifurcation value, both extinction and recovery can happen, and the separatrix of extinction and recovery is the stable manifold at the saddle. In particular, the basin attraction of the extinction state dramatically shrinks as \(\alpha \) increases. Moreover, we identify a theoretical condition for the eradication strategy to work. Additionally, to account for the difficulty of finding females at low levels of the population size, we also incorporate an Allee effect into the TYC model (2.1). Unlike the original model (2.1), the results for the ATYC model (4.1) show that the wild-type females need not have nearly as low population size as that of (2.1) at the optimal termination time, and the remaining sex-reversed supermales are sufficient to eradicate the wild-type females. In addition, we study the possibility of a Turing instability by adding diffusive spatial spread into model (2.1). We find that the inclusion of diffusive spatial spread does not give rise to a Turing instability, which would have suggested that the TYC eradication strategy might be only partially effective, leaving a patchy distribution of the invasive species.

We would like to point out that there are a number of interesting questions at this point, that would make for interesting future investigations. One could explore the optimal control strategy, in this context. For instance, assume that the injection rate of trojan fish, \(\mu \), is a function of time. We could ask: what’s the optimal control for \(\mu (t)\) such that the eradication strategy works and \(\int _{0}^{T} \mu (t)dt\) is minimized for a given amount of time \(T\)? It is also of interest to conduct a bifurcation analysis and consider the Allee effect and inhomogeneous diffusive spatial spread for the partial differential equation model. Here the investigations may have to resort heavily to numerical methods. Another future direction is to consider stochastic models to study the probability of extinction of an invasive species in a finite time, since the results of the deterministic model in (Parshad and Gutierrez 2010) reveal extinction of an invasive species is always possible as time goes to infinity.

All in all, we hope that our results will be of use in further developing the TYC theory. The theory, although limited to species with XY sex determination system that is capable of producing viable progeny during the sex reversal process, is a possible means to combat invasive species of this type.