Effect of electric field induced transmembrane potential on spheroidal cells: theory and experiment

Abstract

The transmembrane potential on a cell exposed to an electric field is a critical parameter for successful cell permeabilization. In this study, the effect of cell shape and orientation on the induced transmembrane potential was analyzed. The transmembrane potential was calculated on prolate and oblate spheroidal cells for various orientations with respect to the electric field direction, both numerically and analytically. Changing the orientation of the cells decreases the induced transmembrane potential from its maximum value when the longest axis of the cell is parallel to the electric field, to its minimum value when the longest axis of the cell is perpendicular to the electric field. The dependency on orientation is more pronounced for elongated cells while it is negligible for spherical cells. The part of the cell membrane where a threshold transmembrane potential is exceeded represents the area of electropermeabilization, i.e. the membrane area through which the transport of molecules is established. Therefore the surface exposed to the transmembrane potential above the threshold value was calculated. The biological relevance of these theoretical results was confirmed with experimental results of the electropermeabilization of plated Chinese hamster ovary cells, which are elongated. Theoretical and experimental results show that permeabilization is not only a function of electric field intensity and cell size but also of cell shape and orientation.

Appendix

Appendix A

In this section, the analytical solution for the induced transmembrane potential Δφ_i on a spheroidal cell is briefly discussed. Under normal physiological conditions the membrane conductance is several orders of magnitude lower than the external medium (Weaver and Chizmadzhev 1996; Kotnik et al. 1997), thus reducing the problem to solving a Laplace equation for a potential φ on a surface of a non-conductive spheroid lying in the external electrical field:

$$ \matrix{ {\Delta \phi (r,\vartheta ,\varphi ) = 0,} & {j_{\rm{n}} \mathop |\limits_S = 0} \cr } $$

(7)

where j _n is the normal component of the electric current at the surface of the spheroid, which for a non-conductive membrane is zero. This is analogous to solving a problem of the potential distribution at the surface of a dielectric spheroid (Stratton 1941). This solution can be extended to the frequency-dependent problem of a spheroid surrounded by a shell having both dielectric and conductive properties, and has been applied to cells by several authors to calculate the frequency-dependent Δφ_i (Schwartz et al. 1965; Bernhardt and Pauly 1973; Zimmermann et al. 1974; Gimsa and Wachner 2001). The solution for a DC case can be correspondingly obtained by solving the Laplace equation in the spheroidal coordinate system, which for parallel orientation has been given by Kotnik and Miklavčič (2000).

The generalized Schwan equation for an arbitrary oriented ellipsoid can be written as:

$$ \Delta \phi _{\rm{i}} = \sum\limits_{i = x,y,z} {r_i E_i } {1 \over {1 - L_i }} $$

(8)

where the r _i is the vector of the point T(x, y, z) lying at the surface of the ellipsoid and L _i are the depolarizing factors in the x, y and z directions and are dependent only on the geometrical properties of the ellipsoid. The sum of the depolarizing factors is always 1.

Analytical equations for depolarizing factors for an ellipsoid can be found in the paper by Stratton (1941). Here we shall limit ourselves only to an axially symmetrical ellipsoid where R ₁>R ₂=R ₃ for a prolate spheroid and R ₁<R ₂=R ₃ for an oblate spheroid. The depolarizing factor for the prolate spheroid along the symmetry axis is:

$$ L_z = {{1 - e^2 } \over {2e^3 }}\left[ {\log {{1 + e} \over {1 - e}} - 2e} \right],\;\;\;\;\;e = \sqrt {1 - \left( {R_2 /R_1 } \right)^2 } $$

(9)

and for the oblate spheroid is:

$$ L_z = {1 \over {e^3 }}\left[ {e - \sqrt {1 - e^2 } \arcsin e} \right],\;\;\;\;\;e = \sqrt {1 - \left( {R_1 /R_2 } \right)^2 } $$

(10)

The depolarizing factors in the other two directions can be calculated from the condition that the sum is equal to one:

$$ L_x = L_y = {1 \over 2}\left( {1 - L_z } \right) $$

(11)

If the z axis of the coordinate system is parallel to the symmetry axis of the spheroid, then the solution for the parallel and perpendicular orientations is:

$$ \matrix{ {\Delta \phi _{{\rm{i}} _\parallel} = zE{1 \over {1 - L_z }},} \hfill & {\Delta \phi _{{\rm{i}} _ \bot} = xE{1 \over {1 - L_x }}} \hfill \cr } $$

(12)

For a sphere where R ₁=R ₂=R, then L _x =L _y =L _z =1/3 and z=R cosϑ; thus from Eq. 12 we obtain:

$$\Delta \phi _{{\rm{i}} \parallel} = \Delta \phi _{{\rm{i}} \bot} = {3 \over 2}RE\cos \vartheta $$

(13)

which is the well-known Schwan equation (Eq. 1). See Table 1.

Table 1. Depolarizing factors L _x , L _y and L _z and normalized maximal induced transmembrane potential Δφ_i/ER ₁ for an oblate spheroid or Δφ_i/ER ₂ for a prolate spheroid for different shapes and orientations. For a sphere (R ₁=R ₂) the normalized induced transmembrane potential is 1.5

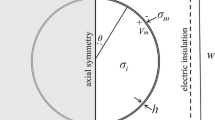
In its most general case the electric field orientation is defined by the angles α (Fig. 1c) and β:

$$ {\bf{E}} = \left( {\matrix{ {E_x } \cr {E_y } \cr {E_z } \cr } } \right) = E\left( {\matrix{ {\sin \alpha \cos \beta } \cr {\sin \alpha \sin \beta } \cr {\cos \alpha } \cr } } \right) $$

(14)

but without loss of generality we can always choose β=0 so the vector of the electric field lies in the xz plane. The point T(x, y, z) at the surface of the spheroid in the spherical coordinates can be written as:

$$ {\bf{r}} = \left( {\matrix{ x \cr y \cr z \cr } } \right) = \left| {\bf{r}} \right|\left( {\matrix{ {\sin \vartheta \cos \varphi } \cr {\sin \vartheta \sin \varphi } \cr {\cos \vartheta } \cr } } \right) $$

(15)

where the absolute value of ∣r∣ is:

$$ \left| {\bf{r}} \right| = {1 \over {\sqrt {{{\cos ^2 \vartheta } \over {R_1^2 }} + {{\sin ^2 \vartheta } \over {R_2^2 }}} }} $$

(16)

Introducing Eqs. 14, 15, 16 into Eq. 8, Δφ_i on an arbitrary oriented spheroid for an infinitely small membrane conductance can be obtained:

$$ \Delta \phi _{\rm{i}} = E{1 \over {\sqrt {{{\cos ^2 \vartheta } \over {R_1^2 }} + {{\sin ^2 \vartheta } \over {R_2^2 }}} }}\left( {\matrix{ {\sin \alpha \cos \beta } \cr {\sin \alpha \sin \beta } \cr {\cos \alpha } \cr } } \right)\left( {\matrix{ {{1 \over {1 - L_x }}\sin \vartheta \cos \varphi } \cr {{1 \over {1 - L_y }}\sin \vartheta \sin \varphi } \cr {{1 \over {1 - L_z }}\cos \vartheta } \cr } } \right) $$

(17)

For β=0 and presented in the Cartesian coordinate system, the above equation simplifies to:

$$ \Delta \phi _{\rm{i}} = E\sin \alpha {1 \over {1 - L_x }}x + E\cos \alpha {1 \over {1 - L_z }}z $$

(18)

This solution is the same as derived by Gimsa and Wachner (2001), only presented in a form that is analogous to the Schwan equation and already taking into account all simplifications that are valid for the cells. Thus from the solution for the induced potential in parallel and perpendicular orientations, one can calculate Δφ_i on an arbitrarily oriented spheroid by means of a linear combination of the two solutions. In other words, in the coordinate system of the spheroid the electric field has two components: in the x and z directions. Since the potential is a linear function, we can simply add the potential induced in the perpendicular direction and the one induced in the parallel direction.

Appendix B

For the calculation of the area where the critical transmembrane potential Δφ_c is exceeded, we have to integrate the surface on the spheroid in spheroidal coordinates τ, ϕ and σ (Korn and Korn 2000). The transformation from Cartesian coordinates to spheroidal coordinates for a prolate spheroid is defined by:

$$ \matrix{ {x^2 } \hfill & = \hfill & {\left( {R_1 ^2 - R_2 ^2 } \right)\left( {\sigma ^2 - 1} \right)\left( {1 - \tau ^2 } \right)\cos ^2 \varphi } \hfill & {\sigma > 1} \hfill \cr {y^2 } \hfill & = \hfill & {\left( {R_1 ^2 - R_2 ^2 } \right)\left( {\sigma ^2 - 1} \right)\left( {1 - \tau ^2 } \right)\sin ^2 \varphi } \hfill & {0 < \varphi < 2\pi } \hfill \cr z \hfill & = \hfill & {\sqrt {R_1 ^2 - R_2 ^2 } \sigma \tau } \hfill & { - 1 < \tau < 1} \hfill \cr } $$

(19)

and for oblate spheroid by:

$$ \matrix{ {x^2 } \hfill & = \hfill & {\left( {R_2 ^2 - R_1 ^2 } \right)\left( {\sigma ^2 + 1} \right)\left( {1 - \tau ^2 } \right)\cos ^2 \varphi } \hfill & {\sigma > 0} \hfill \cr {y^2 } \hfill & = \hfill & {\left( {R_2 ^2 - R_1 ^2 } \right)\left( {\sigma ^2 + 1} \right)\left( {1 - \tau ^2 } \right)\sin ^2 \varphi } \hfill & {0 < \varphi < 2\pi } \hfill \cr z \hfill & = \hfill & {\sqrt {R_2 ^2 - R_1 ^2 } \sigma \tau } \hfill & { - 1 < \tau < 1} \hfill \cr } $$

(20)

The surface element in spheroidal coordinates is (Korn and Korn 2000):

$$ {\rm{d}}S = \sqrt {g_{\varphi \varphi } g_{\tau \tau } } \,{\rm{d}}\varphi \,{\rm{d}}\tau $$

(21)

where g _ϕϕ and g _ττ are elements of the metric tensor in spheroidal coordinates.

The equation of the surface of the spheroid is:

$$ S = R_2 \int\limits_{\tau _1 }^{\tau _2 } {\int\limits_{\varphi _1 }^{\varphi _2 } {\sqrt {R_1 ^2 \left( {1 - \tau ^2 } \right) + R_2 ^2 \tau ^2 } {\rm{d}}\varphi \,{\rm{d}}\tau } } $$

(22)

where ϕ₁, ϕ₂, τ₁ and τ₂ are borders of integration defined by the condition that Δφ_i = Δφ_c. As already mentioned, we analyzed Δφ_i on an ellipse, obtained from the cross-section of a spheroid with the xz plane. For two points on the ellipse where Δφ_c was exceeded, an ellipse on a spheroid through these two points can also be defined, which is perpendicular to plane xz. This ellipse represents our border of integration. The border of integration where Δφ_c has been exceeded is a closed curve on an ellipsoid which is nearly an ellipse. By transforming this ellipse into spheroidal coordinates, the ϕ₁, ϕ₂, τ₁ and τ₂ values are obtained.