Skip to main content

Advertisement

SpringerLink
Log in

Performance enhancement of fin attached ice-on-coil type thermal storage tank for different fin orientations using constrained and unconstrained simulations

  • Original
  • Published:
Heat and Mass Transfer Aims and scope Submit manuscript

Abstract

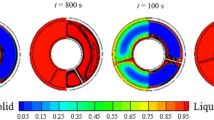
One of the drawbacks in latent thermal energy storage system is the slow charging and discharging time due to the low thermal conductivity of the phase change materials (PCM). This study numerically investigated the PCM melting process inside a finned tube to determine enhanced heat transfer performance. The influences of fin length and fin numbers were investigated. Also, two different fin orientations, a vertical and horizontal type, were examined, using two different simulation methods, constrained and unconstrained. The unconstrained simulation, which considers the density difference between the solid and liquid PCM showed approximately 40 % faster melting rate than that of constrained simulation. For a precise estimation of discharging performance, unconstrained simulation is essential. Thermal instability was found in the liquid layer below the solid PCM, which is contrary to the linear stability theory, due to the strong convection driven by heat flux from the coil wall. As the fin length increases, the area affected by the fin becomes larger, thus the discharging time becomes shorter. The discharging performance also increased as the fin number increased, but the enhancement of discharging performance by more than two fins was not discernible. The horizontal type shortened the complete melting time by approximately 10 % compared to the vertical type.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Abbreviations

a :

Wavenumber (1/m)

C :

Mushy zone constant (kg/m3 s)

c p :

Specific heat (J/kg K)

f :

Volume fraction

g :

Gravitational acceleration (m/s2)

h :

Sensible heat (J/kg)

H :

Enthalpy (J/kg)

k :

Thermal conductivity (W/m K)

l :

Length (m)

L :

Latent heat (J/kg)

p :

Pressure (Pa)

Pr:

Prandtl number ν/α

Ra :

Rayleigh number gβ(T w  − T m )l 3/να

S :

Source term

Ste :

Stefan number c p (T w  − T m )/L

t :

Time (s)

T :

Temperature (K)

u, v :

Velocity components (m/s)

x, y :

Coordinates (m)

α :

Thermal diffusivity (m2/s)

β :

Thermal expansion (1/K)

μ :

Dynamic viscosity (kg/m s)

ν :

Kinematic viscosity (m2/s)

ρ :

Density (kg/m3)

c :

Characteristic

f :

Fin

h :

Hot

H :

Horizontal

i :

Initial

l :

Liquid

m :

Melting

s :

Solid

ref :

Reference

w :

Wall

V :

Vertical

References

  1. Trp A, Lenic K, Frankovic B (2006) Analysis of the influence of operating conditions and geometric parameters on heat transfer in water-paraffin shell-and-tube latent thermal energy storage unit. Appl Therm Eng 26:1830–1839

    Article  Google Scholar 

  2. Hosseini MJ, Ranjbar AA, Sedighi K, Rahimi MA (2012) Combined experimental and computational study on the melting behavior of a medium temperature phase change storage material inside shell and tube heat exchanger. Int Commun Heat Mass 39:1416–1424

    Article  Google Scholar 

  3. Lacroix M (1993) Study of the heat transfer behavior of a latent heat thermal energy storage unit with a finned tube. Int J Heat Mass Transf 36:2083–2092

    Article  Google Scholar 

  4. Erek A, Ilken Z, Acar MA (2005) Experimental and numerical investigation of thermal energy storage with a finned tube. Int J Energ Res 29:283–301

    Article  Google Scholar 

  5. Ismail KAR, Henriquez JR, Moura LFM, Ganzarolli MM (2000) Ice formation around isothermal radial finned tubes. Energ Convers Manage 41:585–605

    Article  Google Scholar 

  6. Zhang Y, Faghri A (1996) Heat transfer enhancement in latent heat thermal energy storage system by using the internally finned tube. Int J Heat Mass 39:3165–3173

    Article  Google Scholar 

  7. Yimer B, Adami M (1997) Parametric study of phase change thermal energy storage systems for space application. Energ Convers Manag 38:253–262

    Article  Google Scholar 

  8. Liu C, Groulx D (2014) Experimental study of the phase change heat transfer inside a horizontal cylindrical latent heat energy storage system. Int J Therm Sci 82:100–110

    Article  Google Scholar 

  9. Sciacovelli A, Gagliardi F, Verda V (2015) Maximization of performance of a PCM latent heat storage system with innovative fins. Appl Energy 137:707–715

    Article  Google Scholar 

  10. Sparrow EM, Geiger GT (1986) Melting in a horizontal tube with the solid either constrained or free to fall under gravity. Int J Heat Mass Transf 29:1007–1019

    Article  Google Scholar 

  11. Hong SW, Lee YT, Chung JD (2015) Restrictions on the analytic approach of unconstrained melting inside a spherical capsule. J Mech Sci Technol 29:5035–5042

    Article  Google Scholar 

  12. Tan FL (2008) Constrained and unconstrained melting inside a sphere. Int Commun Heat Mass 35:466–475

    Article  Google Scholar 

  13. Kozak Y, Rozenfeld T, Ziskind G (2014) Close-contact in vertical annular enclosures with a non-isothermal base: theoretical modeling and application to thermal storage. Int J Heat Mass Transf 72:114–127

    Article  Google Scholar 

  14. Sharifi N, Bergman TL, Faghri A (2011) Enhancement of PCM melting in enclosures with horizontally-finned internal sufaces. Int J Heat Mass Transf 54:4182–4192

    Article  MATH  Google Scholar 

  15. Swaminathan CR, Voller VR (1992) A general enthalpy method for modeling solidification processes. Metall Mater Trans B 23:651–664

    Article  Google Scholar 

  16. Hosseinizadeh SF, Darzi AAR, Tan FL, Khodadadi JM (2013) Unconstrained melting inside a sphere. Int J Therm Sci 63:55–64

    Article  Google Scholar 

  17. Chung JD, Lee JS, Yoo H (1997) Thermal instability during the melting process in an isothermally heated horizontal cylinder. Int J Heat Mass Transf 40:3899–3907

    Article  MATH  Google Scholar 

  18. Chandrasekhar S (1961) Hydrodynamic and Hydro-magnetic stability, Dover edn. Dover Publication, New York

    MATH  Google Scholar 

  19. Sridharan P (2013) Aspect ratio effect on melting and solidification during thermal energy storage. Dissetation, University of South Florida

Download references

Acknowledgments

This research is supported by Korea Institute of Energy Technology Evaluation and Planning (KETEP) granted financial resource from the Ministry of Trade, Industry and Energy of Korea (No. 20132010101780).

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Sejong University, Seoul, 143-747, Korea

    M. H. Kim, X. Q. Duong & J. D. Chung

Authors
  1. M. H. Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. X. Q. Duong
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. D. Chung
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. D. Chung.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kim, M.H., Duong, X.Q. & Chung, J.D. Performance enhancement of fin attached ice-on-coil type thermal storage tank for different fin orientations using constrained and unconstrained simulations. Heat Mass Transfer 53, 1005–1015 (2017). https://doi.org/10.1007/s00231-016-1875-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00231-016-1875-5

Keywords

Search

Navigation