Reproducibility and sensitivity of detecting brain activity by simultaneous electroencephalography and near-infrared spectroscopy

Abstract

The aims were (1) to determine the sensitivity and reproducibility to detect the hemodynamic responses and optical neuronal signals to brain stimulation by near-infrared spectroscopy (NIRS) and evoked potentials by electroencephalography (EEG) and (2) to test the effect of novel filters on the signal-to-noise ratio. This was achieved by simultaneous NIRS and EEG measurements in 15 healthy adults during visual stimulation. Each subject was measured three times on three different days. The sensitivity of NIRS to detect hemodynamic responses was 55.2 % with novel filtering and 40 % without. The reproducibility in single subjects was low. For the EEG, the sensitivity was 86.4 % and the reproducibility 57.1 %. An optical neuronal signal was not detected, although novel filtering considerably reduced noise.

Appendix: Details of PEMAPS

Under this assumption that the heartbeat component is a Fourier series with time-variant fundamental frequency (related to the varying period length) and time-variant coefficients (related to the varying signal shape), the sampled version of the real-valued heartbeat component $x_1, x_2,\,\ldots$ is given as

$$ x_n = \hbox{Re} \left( \sum\limits_{k=1}^K A_{k,n} e^{jk\Uptheta_n} \right) $$

(1)

with coefficients ${A_{0,n} \in \mathbb{R}, A_{1,n},\,\ldots,\,A_{K,n} \in \mathbb{C}}$, phase $\Uptheta_n \in [0,2\pi]$, finite number of frequencies K and

$$ A_{k,n+1} \approx A_{k,n}, $$

(2)

$$ \Uptheta_{n+1} = (\Uptheta_n + \Upomega_n) \bmod 2\pi, $$

(3)

$$ \Upomega_{n+1} \approx \Upomega_n. $$

(4)

Equation (4) expresses the varying heart rate; (2) expresses the varying beat shape. Let the raw NIRS signal vector $\user2{y}=(y_1,\,\ldots,\,y_N)$ be a noisy, trended version of $\user2{x}=(x_1,\,\ldots,\,x_N)$ where N is the signal length. Specifically,

$$ \user2{y} = \user2{A}_{0,-} + \user2{x} + \user2{Z} $$

(5)

where $\user2{Z}=(Z_1,\,\ldots,\,Z_N)$ is discrete time white Gaussian noise, and $\user2{A}_{0,-}=(A_{0,1},\,\ldots,\,A_{0,N})$ models changes slower than the heartbeat and thus is omitted in (1). We will use the vectors $\user2{A}_{k,-} = (A_{k,1},\,\ldots,\,A_{k, N})$ for $k = 0,\,\ldots,\,K$ and decorate estimates with a hat (e.g. $\hat{C}$ is an estimate of C).

Given $\user2{y}$, the objective is to estimate the phases $\varvec{\Uptheta} \,\triangleq\, (\Uptheta_1,\,\ldots,\,\Uptheta_{N}), K$ and the coefficient vectors $\user2{A}_{1,-},\,\ldots,\,\user2{A}_{K,-}$ such that

$$ \sum\limits_{n=1}^{N} (y_n - \hat{x}_n - \hat{A}_{0,n})^2. $$

is minimal, where $\hat{x}_n$ is the reconstructed signal by applying the estimates in (1).

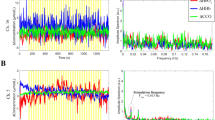
The estimation algorithm consists of several building blocks (see Fig. 3). Initially, the “A ₀ estimator” estimates the slow trend $\user2{A}_{0,-}$ by a one-time procedure similar to low-pass filtering and based on $\user2{y}$ only.

In the heartbeat component, most of the energy, apart from the noise, lies in the fundamental frequency coefficient $\user2{A}_{1,-}$. Thus, a first rough estimate of the heartbeat component is a complex sinusoid with constant complex magnitude. The “Initial A1 estimator” block makes an estimate $\tilde{A}_1$ of this magnitude such that the sinusoid has approximately the same energy as $\user2{y} - \hat{\user2{A}}_{0,-}$.

The “Phase estimator” calculates the final estimate $\hat{\varvec{\Uptheta}}$ of $\varvec{\Uptheta}$ based on estimates $\hat{\user2{A}}_{0,-}$ and $\tilde{A}_1$ and (1) with K = 1 parameterized as

$$ \begin{aligned} x_n &= \hbox{Re} \left(\tilde{A}_1 \cdot e^{j\Uptheta_n} \right) \\ &= \hbox{Re}(\tilde{A}_1)\cos(\Uptheta_n) - \hbox{Im}(\tilde{A}_1)\sin(\Uptheta_n) \\ &= \hat{\user2{A}}_1 \cdot \user2{C}_n \end{aligned} $$

(6)

with constant vector $\hat{\user2{A}}_1 = \left(\hbox{Re} (\tilde{A}_1), -\hbox{Im}(\tilde{A}_1)\right)$, state vector $\user2{C}_n = \left(\cos(\Uptheta_n), \sin(\Uptheta_n) \right)^T$ and state transition

$$ \user2{C}_n = \hbox{rot}(\hat{\Upomega}) \cdot \user2{C}_{n-1} + \user2{U}_n $$

(7)

where

$$ \hbox{rot}(\Upomega) = \left( \begin{array}{cc} \cos(\hat{\Upomega})&-\sin(\hat{\Upomega}) \\ \sin(\hat{\Upomega}) & \cos(\hat{\Upomega}) \end{array} \right) $$

is a rotation matrix, and $\hat{\Upomega}$ is an a priori estimate of $\Upomega_n$ in (4). $\hat{\Upomega}$ is derived using the formula in Trajkovic et al. (2009), section “Optical neuronal signal,” paragraph 4 and assuming a typical heart rate depending on the subject, for example H = 80 bpm for adults. Since $\hat{\Upomega}$ is fixed, despite the fact that the heart rate varies considerably depending on various factors, uncertainty, that is two-dimensional zero-mean white Gaussian noise $\user2{U}_n$, is added to the rotated state in (7). This addition of noise defines (4).

The estimate $\hat{\user2{C}}_n$ of $\user2{C}_n$ is made as

$$ \hat{\user2{C}}_n = \mathop{\hbox{arg max}}\limits_{\user2{C}_n} f(\user2{C}_n \,|\, \user2{A}_{0,-}, \tilde{A}_1, \user2{y}). $$

(8)

The function f in (8) (1) comprises (5), (6) and (7) and (2) is derived with the message passing algorithm described in Trajkovic et al. (2012), section “Method.”

Each estimate $\hat{\Uptheta}_n$ in $\hat{\varvec{\Uptheta}}$ is made as

$$ \hat{\Uptheta}_n = \arctan \frac{\hat{\user2{C}}_n(2)}{\hat{\user2{C}}_n(1)} $$

(9)

with $\hat{\user2{C}}_n(i)$ denoting the i-th entry of the vector $\hat{\user2{C}}_n$.

The “Coefficient estimator” calculates the full set of coefficient estimates $\hat{\user2{A}}_{1,-},\,\ldots,\,\hat{\user2{A}}_{K,-}$. Each estimate $\hat{A}_{k,n}$ of A _k,n is calculated based on the estimates $\hat{\user2{A}}_{k-1,-},\,\ldots,\,\hat{\user2{A}}_{0,-}, \hat{\varvec{\Uptheta}}$ and $\user2{y}$ as

$$ \hat{\user2{A}}_{k,n} = \underset{A_{k,n} \in \mathbb C}{\hbox{arg max}}\,g(A_{k,n} \vert \hat{\user2{A}}_{k-1,-},\,\ldots,\,\hat{\user2{A}}_{0,-}, \hat{\varvec{\Uptheta}}, \user2{y}) $$

(10)

for increasing k. The function g in (10) (i) comprises (1), (2) and the assumption of white Gaussian noise in (5) and (ii) is derived with the message passing algorithm described in Trajkovic (2010), section “The new coefficient estimator.”

The “Regularization” block is used to iteratively derive the number of harmonics K in (1) as described in Trajkovic et al. (2012), at the end of section “Method.”

The “Eq. (1)” block reconstructs the heartbeat component by applying the estimates $\hat{\user2{A}}_{1,-},\,\ldots,\,\hat{\user2{A}}_{K,-}$ and $\hat{\varvec{\Uptheta}}$ in (1).