Abstract
We consider generalized gradient systems with rate-independent and rate-dependent dissipation potentials. We provide a general framework for performing a vanishing-viscosity limit leading to the notion of parametrized and true Balanced-Viscosity solutions that include a precise description of the jump behavior developing in this limit. Distinguishing an elastic variable u having a viscous damping with relaxation time \(\varepsilon ^\alpha \) and an internal variable z with relaxation time \(\varepsilon \) we obtain different limits for the three cases \(\alpha \in (0,1)\), \(\alpha =1\) and \(\alpha >1\). An application to a delamination problem shows that the theory is general enough to treat nontrivial models in continuum mechanics.
Similar content being viewed by others
List of symbols | ||
|---|---|---|
\({\textbf{U}}, {\textbf{Z}}\) | State spaces | (1.1) |
\({\textbf{Q}}= {\textbf{U}}{\times }{\textbf{Z}}\) | Overall state space | |
\( {\textbf{U}}_{{\textrm{e}}}\subset {\textbf{U}}, \ {\textbf{Z}}_{{\textrm{e}}}\Subset {\textbf{Z}}\) | Energy spaces | Hypothesis 4.1 |
\({\textbf{Z}}_{{\textrm{ri}}}\supset {\textbf{Z}}\) | Space for 1-homogeneous dissipation potential | Hypothesis 4.1 |
\({{\mathcal {R}}}: {\textbf{Z}}_{{\textrm{ri}}}\rightarrow [0,\infty ) \) | 1-homogeneous dissipation potential | Hypothesis 4.2 |
\({{\mathcal {V}}}_{\textsf{u}} : {\textbf{U}}\rightarrow [0,\infty )\), \({{\mathcal {V}}}_{\textsf{z}} : {\textbf{Z}}\rightarrow [0,\infty )\) | Viscous dissipation potentials | Hypothesis 4.2 |
\({{\mathcal {V}}}_{\textsf{x}}^*: \textbf{X}^* \rightarrow [0,\infty )\), \( \textbf{X} \in \{ {\textbf{U}}, {\textbf{Z}}\}\) | Legendre–Fenchel conjugate of \({{\mathcal {V}}}_{\textsf{x}}\) for \(\textsf{x} \in \{ {\textsf{u}}, {\textsf{z}}\} \) | Definition 3.1 |
\({\mathcal {W}}_{\textsf{z}}^*: {\textbf{Z}}^* \rightarrow [0,\infty )\) | Conjugate of \({{\mathcal {R}}}{+}{{\mathcal {V}}}_{\textsf{z}}\) | (4.17) |
\({{\mathcal {V}}}_{\textsf{x}}^{\lambda }, \textsf{x} \in \{ {\textsf{u}},{\textsf{z}}\}, \lambda \in (0,\infty ) \) | Rescaled viscous dissipation potentials | (1.5a) |
\(\Psi _{\varepsilon ,\alpha } = {{\mathcal {V}}}_{\textsf{u}}^{\varepsilon ^\alpha } + {{\mathcal {R}}}+ {{\mathcal {V}}}_{\textsf{z}}^{\varepsilon }\) | Overall viscous potential | (1.7) |
\({{\mathcal {E}}}: [0,T]\times {\textbf{U}}{\times }{\textbf{Z}}\rightarrow (-\infty ,+\infty ]\) | Driving energy functional | Hypothesis 4.3 |
\(\mathcal {S}_E\), \(E>0\) | Energy sublevels | (4.8) |
\(\partial _q {{\mathcal {E}}}\) | Fréchet subdifferential of \({{\mathcal {E}}}(t,\cdot )\) | (4.10) |
\({\mathscr {S}}_{\textsf{x}}^*: [0,T]{\times }{\mathscr {D}}\rightarrow [0,\infty ] \) | Generalized slope functional for \(\textsf{x} \in \{ {\textsf{u}}, {\textsf{z}}\} \) | (4.19) |
\({\mathfrak {A}}_{\textsf{x}}^{*}(t,q), \ (t,q)\in [0,T]{\times }{\mathscr {D}}\) | Set of minimizers for the slope \( {\mathscr {S}}_{\textsf{x}}^*(t,q), \ \textsf{x} \in \{ {\textsf{u}}, {\textsf{z}}\}\) | (4.21) |
\( {\mathscr {G}}^{\alpha }[t,q], \ (t,q)\in [0,T]{\times }{\mathscr {D}}\) | Sets of positivity for the slopes at (t, q) | (5.20) |
\({\mathcal {B}}_\psi \) | B-function associated with a dissipation potential \(\psi \) | (3.1) |
\({\mathfrak {b}}_\psi \) | Vanishing-viscosity contact potential assoc. with \(\psi \) | (3.4) |
\({\mathfrak {B}}_\varepsilon ^\alpha \), \(\varepsilon \ge 0\), | Rescaled joint B-function | (3.16) |
\({\mathfrak {M}}_\varepsilon ^\alpha \), \(\varepsilon >0\), | Rescaled joint M-function | (5.1) |
\({\mathfrak {M}}_0^\alpha \) | (Limiting) rescaled joint M-function | (5.7) |
\({\mathfrak {M}}_0^{\alpha , \textrm{red}}\) | Reduced rescaled joint M-function | (5.11) |
\({\textrm{AC}}([a,b];{{\mathcal {R}}},{\textbf{Z}})\) | \({{\mathcal {R}}}\)-absolutely continuous curves from [a, b] to \({\textbf{Z}}\) | (5.18) |
\(\mathscr {A}([a,b];[0,T]{\times }{\textbf{Q}})\) | Admissible parametrized curves from [a, b] to \([0,T]{\times }{\textbf{Q}}\) | Definition 5.6 |
\( {\mathcal {A}}_{t}(q_0,q_1) \) | Admissible transition curves betw. \(q_0\) and \(q_1\) at time t | Definition 5.6 |
\(\Sigma _\alpha \) | Contact set | (5.42) |
\({\textrm{A}}_{\textsf{u}} {\textrm{C}}_{\textsf{z}} = {\textrm{A}}_{\textsf{u}} \cap {\textrm{C}}_{\textsf{z}}\) | Evolution regimes with \(\mathrm {A \in \{E,V,B\}} \text { and } \mathrm {C \in \{R,V,B\} }\) | (5.45) |
\({\textrm{Var}}_{{{\mathcal {R}}}}\) | \({{\mathcal {R}}}\)-variation | (6.2) |
\( \textrm{J}[q] \) | Jump set of a true \(\text {BV}\) solution | Definition 6.3 |
\( {\textrm{cost}}_{{\mathfrak {M}}_{0}^{\alpha }}\) | Finsler cost induced by \( {\mathfrak {M}}_{0}^{\alpha }\) | (6.6) |
\( {\textrm{Var}}_{{\mathfrak {M}}_{0}^{\alpha }} \) | Total variation induced by \({\mathfrak {M}}_{0}^{\alpha }\) | (6.8) |
1 Introduction
In this paper we address rate-independent limits of viscous evolutionary systems that are motivated by applications in solid mechanics. These systems can be described in terms of two variables \(u\in {\textbf{U}}\) and \( z\in {\textbf{Z}}\); throughout, we shall assume that the state spaces
Typically, u is the displacement, or the deformation of the body, whereas z is an internal variable specific of the phenomenon under investigation, in accordance with the theory of generalized standard materials, see [18].
1.1 Rate-Independent Systems
Under very slow loading rates, one often assumes that u satisfies a static balance law that arises as Euler–Lagrange equation from minimizing the energy functional \({{\mathcal {E}}}\) with respect to u. The evolution of z is governed by a (doubly nonlinear) subdifferential inclusion featuring the z-derivative of the energy and the viscous force in form of the subdifferential \(\partial {{\mathcal {R}}}\) of a dissipation potential \({{\mathcal {R}}}\):
If \({{\mathcal {R}}}: {\textbf{Z}}\rightarrow [0,\infty ]\) is positively homogeneous of degree 1, i.e. \({{\mathcal {R}}}(\lambda z')=\lambda {{\mathcal {R}}}(z')\) for all \(\lambda >0\), then the system (1.2) is called rate-independent, and the triple \(({\textbf{U}}{\times }{\textbf{Z}},{{\mathcal {E}}},{{\mathcal {R}}})\) is called a rate-independent system, cf. [33].
Here, \(\partial {{\mathcal {R}}}: {\textbf{Z}}\rightrightarrows {\textbf{Z}}^*\) denotes the subdifferential of convex analysis for the nonsmooth functional \({{\mathcal {R}}}\), whereas, throughout this introduction, for simplicity we will assume that the (proper) energy functional \({{\mathcal {E}}}: [0,T]{\times }{\textbf{U}}{\times }{\textbf{Z}}\rightarrow (-\infty ,\infty ]\), which is smooth with respect to time, is additionally smooth with respect to both variables u and z. System (1.2) reflects the ansatz that energy is dissipated through changes of the internal variable z only: in particular, the doubly nonlinear evolution inclusion (1.2b) balances the dissipative frictional forces from \(\partial {{\mathcal {R}}}(z')\) with the restoring force \({\textrm{D}}_z {\mathcal {E}}(t,u, z)\). Despite the assumed smoothness of \((u,z) \mapsto {\mathcal {E}}(t,u, z)\), system (1.2) is only formally written; due to the 1-homogeneity of \({{\mathcal {R}}}\), one can in general expect only \(\text {BV}\)-time regularity for z. Thus z may have jumps as a function of time and the pointwise derivative \(z'\) in the subdifferential inclusion (1.2b) need not be defined. This has motivated the development of various weak solution concepts for system (1.2).
Energetic solutions were advanced in the late ’90 s in [34, 35, 37] for abstract rate-independent systems, and in the context of phase transformations in solids. In the realm of crack propagation, an analogous notion of evolution was pioneered in [15] and later further developed in [12] with the concept of ‘quasistatic evolution’. Due to its flexibility, the energetic concept has been successfully applied to a wide scope of problems, see e.g. [33] for a survey.
1.2 The Vanishing-Viscosity Approach
However, it has been observed that the energetic notion may fail to provide a feasible description of the system behavior at jumps, in the case of a nonconvex driving energy. This fact has motivated the introduction of an alternative weak solvability concept, first suggested in [14] and based on the vanishing-viscosity regularization of the rate-independent system as a selection criterion for mechanically feasible weak solutions. In the context of system (1.2), this ‘viscous regularization’ involves a second (lower semicontinuous, convex) dissipation potential \( {{\mathcal {V}}}_{\textsf{z}}: {\textbf{Z}}\rightarrow [0,+\infty )\), with superlinear growth at infinity; to fix ideas, we may think of a quadratic potential. The vanishing-viscosity approach then consists in performing the asymptotic analysis of solutions to the rate-dependent system
as the viscosity parameter \(\varepsilon \rightarrow 0^+\). System (1.3) now features two rates: in addition to that of the external loading, scaling as \(\varepsilon ^0=1\), the internal rate of the system, set on the faster scale \(\varepsilon \), is revealed. In diverse (finite-dimensional, infinite-dimensional, and even metric) setups, cf. [14, 36, 38, 39, 42] (see also [21] and [47]), solutions to the ‘viscous system’ have been shown to converge to a different type of solution of (1.2), which we shall refer to as Balanced-Viscosity solution, featuring a better description of the jumps of the system. In parallel, the vanishing-viscosity approach has proved to be a robust method in manifold applications, ranging from plasticity (cf. e.g. [4, 13, 16]), to fracture [22, 26, 45], damage and fatigue [1, 9, 23], and to optimal control [59] to name a few.
This paper revolves around a different, but still of vanishing-viscosity type, solution notion for system (1.2). Indeed, we are going to regularize it by considering a viscous approximation of (1.2a), besides the viscous approximation (1.3b) of (1.2b). Therefore, we will address the asymptotic analysis as \(\varepsilon \rightarrow 0^+\) of the system of doubly nonlinear differential inclusions
where for \({\textsf{x}}\in \{{\textsf{u}}, {\textsf{z}}\}\) we have set that
(the functional \({{\mathcal {V}}}_{\textsf{x}}^{\infty }\) will indeed come into play later on, cf. (1.13)). Throughout we assume that \({{\mathcal {V}}}_{\textsf{x}}\) satisfies \({{\mathcal {V}}}_{\textsf{x}}(0)=0\), \(\partial {{\mathcal {V}}}_{\textsf{x}}(0)=\{0\}\), and has superlinear growth, which implies that \({{\mathcal {V}}}_{\textsf{x}}^{0}\) and \({{\mathcal {V}}}_{\textsf{x}}^{\infty }\) are indeed the Mosco limits of \({{\mathcal {V}}}_{\textsf{x}}^{\lambda }\) for \(\lambda \rightarrow 0^+\) and \(\lambda \rightarrow \infty \), respectively. We will use that the subdifferentials take the form
The parameter \(\alpha \) in (1.4a) determines which of the two variables u and z relaxes faster to equilibrium and rate-independent evolution, respectively. Hence, following the finite-dimensional work [43] we shall refer to (1.4) as a multi-rate system, with the time scale \(\varepsilon ^0=1\) of the external loading and the (possibly different) relaxation times \(\varepsilon \) and \(\varepsilon ^\alpha \) of the variables z and u.
From a broader perspective, with our analysis we aim to contribute to the investigation of coupled rate-dependent/rate-independent phenomena, a topic that has attracted some attention over the last decade. In this connection, we may mention the study of systems with a mixed rate-dependent/rate-independent character (typically, a rate-independent flow rule for the internal variable coupled with the momentum balance, with viscosity and inertia, for the displacements, and possibly with the heat equation), see the series of papers by T. Roubíček [52,53,54,55,56], among others. There, a weak solvability notion, still of energetic type, was advanced, cf. also [28, 50].
However, unlike in those contributions, in our ‘modeling’ approach the balanced interplay of rate-dependent and rate-independent behavior does not stem from coupling equations with a rate-dependent and a rate-independent character. Instead, it emerges through the asymptotic analysis as \(\varepsilon \rightarrow 0^+\) of the ‘viscous’ system (1.4), which leads to a solution of the rate-independent one (1.2) that is ‘reminiscent of viscosity’, in both variables u and z, in the description of the system behavior at jumps. This ‘full’ vanishing-viscosity approach, also involving the displacement variable u, has been already carried out for a model for fracture evolution with pre-assigned crack path in [46], as well as in the context of perfect plasticity [11, 48] and delamination [58]. With different techniques, based on an alternating minimization scheme, the emergence of viscous behavior both for the displacement and for the internal variable is demonstrated in [20] for a phase-field type fracture model.
In this mainstream, in [43] we have addressed the vanishing-viscosity analysis of (1.4) in a preliminary finite-dimensional setting, with \({\textbf{U}}= {\mathbb {R}}^n\) and \({\textbf{Z}}= {\mathbb {R}}^m\), and for a smooth energy \({{\mathcal {E}}}\in {\textrm{C}}^1([0,T]{{\times }}{\mathbb {R}}^n{{\times }}{\mathbb {R}}^m)\), with the aim of emphasizing the role of viscosity in the description of the jump behavior of the limiting rate-independent system. Even in this significantly simplified setup, the analysis in [43] conveyed how the balanced interplay of the different relaxation rates in (1.4) enters in the description of the jump dynamics of the rate-independent system. In particular, it showed that viscosity in u and viscosity z determine the jump transition path in different ways depending on whether the parameter \(\alpha \) is strictly bigger than, or equal to, or strictly smaller than 1.
The aim of this paper is to thoroughly extend the results from [43] to an infinite-dimensional and non-smooth setting, suited for the application of this vanishing-viscosity approach to models in solid mechanics. What is more, we will also broaden the analysis in [43], which is confined to the case of quadratic ‘viscous’ dissipation potentials, to a fairly general class of potentials \({{\mathcal {V}}}_{\textsf{u}}\) and \({{\mathcal {V}}}_{\textsf{z}}\).
1.3 Our Results
Throughout most of this paper, we will confine the discussion to the abstract rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) arising in the vanishing-vis-cosity limit of (1.4). The notation looks a bit extensive, but has the advantage of emphasizing the dependence of the solution concept on the energy functional \({{\mathcal {E}}}\), the three different types of dissipation \({{\mathcal {V}}}_{\textsf{u}}\), \({{\mathcal {R}}}\), and \({{\mathcal {V}}}_{\textsf{z}}\), and the parameter \(\alpha >0\). This also explains the name “Balanced-Viscosity solution” that suggests the appearance of the viscous effects by balancing the influence of \({{\mathcal {R}}}\), \({{\mathcal {V}}}_{\textsf{x}}\), and \({{\mathcal {V}}}_{\textsf{z}}\) in such a way that the energy-dissipation balance remains true. Of course, using the abbreviation “BV solution” should remind us about the fact that these solutions may not be continuous but may have jumps as functions of time.
In our opinion, in that general framework the main ideas underlying the vanishing-viscosity approach are easier to convey. Indeed, we aim to provide some possible recipes for the application of this approach to concrete rate-independent limiting processes, where of course the ‘abstract techniques’ may have to be suitably adjusted to the specific situation. For this, we will strive to work in a fairly general setup,
-
(1)
encompassing nonsmoothness of the energies \(u\mapsto {\mathcal {E}}(t,u, z)\) and \(z\mapsto {\mathcal {E}}(t,u, z)\) through the usage of suitable subdifferentials \(\partial _{\textsf{u}}{{\mathcal {E}}}:[0,T]{\times }{\textbf{U}}{\times }{\textbf{Z}}\rightrightarrows {\textbf{U}}^*\) and \(\partial _{\textsf{z}}{{\mathcal {E}}}:[0,T]{\times }{\textbf{U}}{\times }{\textbf{Z}}\rightrightarrows {\textbf{Z}}^*\) in place of the Gâteau derivatives \({\textrm{D}}_u {{\mathcal {E}}}\) and \({\textrm{D}}_z {{\mathcal {E}}}\), and
-
(2)
allowing for a wide range of ‘viscous dissipation potentials’ \({{\mathcal {V}}}_{\textsf{u}}\) and \({{\mathcal {V}}}_{\textsf{z}}\). In particular, we shall allow for a much broader class of dissipation potentials \({{\mathcal {V}}}_{\textsf{z}}\) than those considered in [42].
The first cornerstone of our vanishing-viscosity analysis is the observation that the viscous system (1.4) has the structure of a generalized gradient system (cf. [31]); indeed, it can be rewritten as
with \(q=(u,z)\in {\textbf{Q}}= {\textbf{U}}{\times }{\textbf{Z}}\) and
In turn, (1.6) can be equivalently formulated using the single energy-dissipation balance
for all \(0 \le s\le t \le T\), featuring the M-function
with the Legendre–Fenchel conjugate \(\Psi _{\varepsilon ,\alpha }^*\) of \(\Psi _{\varepsilon ,\alpha }\). This reformulation is often referred to energy-dissipation principle; the germs of this idea trace back to E. De Giorgi’s variational theory for gradient flows in [2], see also [3, Prop. 1.4.1] and [31, Thm. 3.2]. In our setup, it is based on the validity of a suitable chain rule for \({{\mathcal {E}}}\), which will be thoroughly discussed in the sequel.
From (1.8) we obtain the basic a priori estimates on a sequence \((u_\varepsilon ,z_\varepsilon )_\varepsilon \) of solutions to (1.4). However, such bounds are not enough to pass to the limit, as they do not provide sufficient compactness for the variable u. For all of our existence results we will additionally impose the \({\textrm{L}}^1\)-bound
In Sect. 4.6 we show how this condition can be derived under suitable conditions on the coupling of the u and z variables. Relying on the estimates (1.8) and (1.10), we are able to reparametrize the curves \((q_\varepsilon )_\varepsilon = (u_\varepsilon ,z_\varepsilon )_\varepsilon \) by their “dissipation arclength” \( {\textsf{s}}_\varepsilon : [0,T] \rightarrow [0, {{{\textsf {S}}}}_\varepsilon ]\) given by
Reparametrization was first advanced in [14] as a tool to capture the viscous transition paths, at jumps, in the rate-independent limit. With this aim, first of all we observe that, setting \({\textsf{t}}_\varepsilon : = {\textsf{s}}_\varepsilon ^{-1}: [0,,{{{\textsf {S}}}}_\varepsilon ]\rightarrow [0,T]\) and \({\textsf{u}}_\varepsilon : = u_\varepsilon \circ {\textsf{t}}_\varepsilon \), \({\textsf{z}}_\varepsilon : = z_\varepsilon \circ {\textsf{t}}_\varepsilon \), the rescaled curves \(({\textsf{t}}_\varepsilon , {\textsf{u}}_\varepsilon ,{\textsf{z}}_\varepsilon )_\varepsilon \) satisfy a reparametrized version of (1.8). Using the first main results of this paper presented in Theorems 5.12 and 5.15, we are able to pass to the limit in this reparametrized energy balance as \(\varepsilon \rightarrow 0^+\) and obtain a triple \(({\textsf{t}},{\textsf{q}}) = ({\textsf{t}},{\textsf{u}},{\textsf{z}}): [0,{{{\textsf {S}}}}]\rightarrow [0,T]{\times }{\textbf{U}}{\times }{\textbf{Z}}\) satisfying the energy-dissipation balance
which encodes all the information on the behavior of the limiting rate-independent system in the expression of the ‘time-space dissipation function’ \({\mathfrak {M}}_{0}^{\alpha }\), thoroughly investigated in Sect. 5.1. We shall call a triple \(({\textsf{t}},{\textsf{u}},{\textsf{z}})\) complying with (1.11) a parametrized Balanced-Viscosity (\(\text {pBV}\), for short) solution to the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\).
We highlight two main properties of this solution concept that follow from the special form of \({\mathfrak {M}}_{0}^{\alpha }\):
-
When a solution does not jump, i.e. when the function \({\textsf{t}}\) of the artificial time s, recording the (slow) external time scale, fulfills \({\textsf{t}}'(s)>0\), the term \({\mathfrak {M}}_{0}^{\alpha }({\textsf{t}},{\textsf{q}}, {\textsf{t}}',{\textsf{q}}') \) is finite if and only if \({\textsf{u}}\) is stationary and \({\textsf{z}}\) is locally stable, i.e.
$$\begin{aligned} -{\textrm{D}}_u {\mathcal {E}}({\textsf{t}}(s),{\textsf{u}}(s), {\textsf{z}}(s)) =0\;\text {in}\; {\textbf{U}}^* \;\,\text {and}\;\, -{\textrm{D}}_z {\mathcal {E}}({\textsf{t}}(s),{\textsf{u}}(s), {\textsf{z}}(s)) \in \partial {{\mathcal {R}}}(0)\;\text {in}\; {\textbf{Z}}^*. \end{aligned}$$Because of the local character of the second condition, the unfeasible jumps that may occur in ‘energetic solutions’ via their ‘global stability’ are thus avoided.
-
The function \({\mathfrak {M}}_{0}^{\alpha }\) in (1.11) comprises the contributions of the dissipation potentials \({{\mathcal {R}}}\), \({{\mathcal {V}}}_{\textsf{u}}\) and \({{\mathcal {V}}}_{\textsf{z}}\) by condensing the viscous effects into a description of the limiting jump behavior that can occur only if \({\textsf{t}}'(s)=0\), i.e. the slow external time is frozen. For example, if the dissipation potentials \({{\mathcal {V}}}_{\textsf{u}}\) and \({{\mathcal {V}}}_{\textsf{z}}\) are p-homogeneous (i.e. \({{\mathcal {V}}}_{\textsf{x}}(\lambda {\textsf{x}}')=\lambda ^p {{\mathcal {V}}}_{\textsf{x}}({\textsf{x}}')\) for \(\lambda >0\)), then for \(\alpha =1\) and \({\textsf{t}}'=0\) we have
$$\begin{aligned}&{\mathfrak {M}}_{0}^{1}({\textsf{t}},({\textsf{u}},{\textsf{z}}), 0,({\textsf{u}}',{\textsf{z}}')) = {{\mathcal {R}}}({\textsf{z}}') \nonumber \\&\quad + {\widehat{c}}_p \, \big ({{\mathcal {V}}}_{\textsf{z}} ({\textsf{z}}'){+} {{\mathcal {V}}}_{\textsf{u}} ({\textsf{u}}')\big )^{1/p} \,\big ( {{\mathcal {V}}}_{\textsf{u}}^*({-}{\textrm{D}}_u {\mathcal {E}}({\textsf{t}},{\textsf{u}}, {\textsf{z}})) {+} {\mathcal {W}}_{\textsf{z}}^*({-}{\textrm{D}}_z {\mathcal {E}}({\textsf{t}},{\textsf{u}}, {\textsf{z}})) \big )^{1{-}1/p} \end{aligned}$$(1.12)(see Example 5.3). The symmetric role of \({{\mathcal {V}}}_{\textsf{u}} \) and \({{\mathcal {V}}}_{\textsf{z}}\) in (1.12) arises because of \(\alpha =1\) and reflects the fact that, at a jump, the system may switch to a viscous regime where both dissipation mechanisms intervene in the evolution of u and z, respectively. In contrast, for \(\alpha >1\) and \(\alpha <1\), the M-function \({\mathfrak {M}}_{0}^{\alpha }\) shows the different roles of \({{\mathcal {V}}}_{\textsf{u}} \) and \({{\mathcal {V}}}_{\textsf{z}}\), cf. (5.12).
These features are even more apparent in the characterization of a suitable class of \(\text {pBV}\) solutions in terms of a system of subdifferential inclusions that has the very same structure as the original viscous system (1.4) as provided by Theorem 5.21. This result shows that a triple \(({\textsf{t}},{\textsf{u}},{\textsf{z}}): [0,{{{\textsf {S}}}}]\rightarrow [0,T] {\times }{\textbf{U}}{\times }{\textbf{Z}}\) is an enhanced \(\text {pBV}\) solution if and only if there exist measurable functions \(\lambda _{\textsf{u}}, \lambda _{\textsf{z}}:[0,{{{\textsf {S}}}}] \rightarrow [0,\infty ]\) such that for almost all \(s\in (0,{{{\textsf {S}}}})\) we have
In (1.13b) and (1.13c) we use the obvious conventions \(\frac{\infty }{1+\infty }=1\) and \(\frac{1}{1+\infty }=0\), respectively. Condition (1.13b) entails that the coefficients \(\lambda _{\textsf{u}}(s)\) and \(\lambda _{\textsf{z}}(s)\) of the ‘viscous terms’ in (1.13a) are allowed to be nonzero only when \({\textsf{t}}'(s)=0\), i.e. viscous behavior may manifest itself only at jumps happening now at a fixed time \(t_*={\textsf{t}}(s)\) for \(s\in [s_0,s_1]\). Conditions (1.13c) reveal that the onset of viscous effects in u and/or in z depends on whether u relaxes to equilibrium faster (case \(\alpha >1\)), with the same speed (case \(\alpha =1\)), or more slowly (case \(\alpha <1\)), than z relaxes to local stability. In particular, the case \(\lambda _{\textsf{x}}=\infty \) leads to a blocking of the variable \({\textsf{x}}\in \{{\textsf{u}},{\textsf{z}}\}\), i.e. \({\textsf{x}}'(s)=0\) and \(\partial {{\mathcal {V}}}_{\textsf{x}}^{\infty }(0) =\textbf{Z}^*\). These aspects will be thoroughly explored in Sects. 2 and 5.5.
Finally, in analogy with the case of the ‘single-rate’ vanishing-viscosity approach developed in [39, 42], here as well we introduce “true Balanced-Viscosity solutions” (shortly referred to as BV solutions) as the non-parametrized counterpart to \(\text {pBV}\) solutions, see Definition 6.5. These solutions are functions of the original time variable \(t\in [0,T]\) and fulfill an energy balance that again encompasses the contribution of the viscous dissipation potentials \({{\mathcal {V}}}_{\textsf{u}}\) and \({{\mathcal {V}}}_{\textsf{z}}\) to the description of energy dissipation at jump times of the solution. We are going to show that true \(\text {BV}\) solutions are related to \(\text {pBV}\) solutions in a canonical way, see Theorem 6.15. What is more, in Theorems 6.8 and 6.12 we provide general assumptions that guarantee that all pointwise-in-time limits of a family of (non-parametrized) viscous solutions \(q_{\varepsilon _k}:[0,T]\rightarrow {\textbf{Q}}\), for \({\varepsilon _k}\rightarrow 0^+\), are indeed \(\text {BV}\) solutions.
We emphasize that the definition of BV solutions is independent of the vanishing-viscosity approach. This independence guarantees that the solution concept is indeed stable under parameter variations in the way shown in [41, Thm. 4.8] for generalized gradient systems (cf. also [40, Thm. 4.2]). Otherwise, doing the limit \(\varepsilon \rightarrow 0^+\) first and then a parameter limit \(\delta \rightarrow \delta _*\) it is not possible to show that the obtained limit curve is a vanishing-viscosity limit for fixed \(\delta _*\), see Remark 6.9. In principle, our general definition of (parametrized) BV solutions for limiting rate-independent systems can be used and analyzed independently of the vanishing-viscosity approach. However, to avoid overburdening the present work we do not follow this line and restrict ourselves to situations where existence of solutions can be established exactly by these methods. After all, this is the mechanical motivation for considering such solution classes.
1.4 Application to a Model for Delamination
In Sect. 8 we show that our existence results for \(\text {pBV}\) solutions, characterized by (1.13), and (true) \(\text {BV}\) solutions apply to a rate-independent process modeling delamination between two elastic bodies in adhesive contact along a prescribed interface. For a first approach to energetic solutions for this delamination problem, we refer to [25]. A systematic approach to BV solutions for a multi-rate system involving elastoplasticity and damage is given in [10].
The vanishing-viscosity analysis for the viscously regularized delamination model poses nontrivial challenges due to the presence of various maximal monotone nonlinearities, in the displacement equation and in the flow rule for the delamination variable z, which for instance render the constraints \(z(t,x) \in [0,1]\) and the unidirectionality of the evolution. In particular, the main challenge is to obtain the a priori estimate (1.10) uniformly in \(\varepsilon \) when taking the vanishing-viscosity limit, see Proposition 8.4. For this, it is necessary to carefully regularize the viscous system. Because of the relatively weak coupling between the displacement equation and the flow rule for z, the smoothened system possesses a semilinear structure that allows us to apply the techniques developed in [30, Sec. 4.4] and [36, Sec. 2], see Sect. 8.4.
1.5 Plan of the Paper
In Sect. 2 we introduce a prototype of the coupled systems that we aim to mathematically model through the Balanced-Viscosity concept. In this simplified context, avoiding technicalities we illustrate the notion of (parametrized) \(\text {BV}\) solution and its mechanical interpretation.
Section 3 contains some auxiliary tools on that will be central for the rest of the paper. It revolves around the construction of vanishing-viscosity contact potential that will be relevant for describing the dissipative behavior of the viscously regularized system in the multi-rate case with 1, \(\varepsilon \), and \(\varepsilon ^\alpha \). In fact, it will enter into the definition of the function \({\mathfrak {M}}_{0}^{\alpha }\) in (1.11). Since in this paper we will extend the analysis of [43] to general viscous dissipation potentials, we will not be able to explicitly calculate the related vanishing-viscosity contact potential except for particular cases. Thus, a large part of Sect. 3 will focus on the derivation of general properties of contact potentials that will lay the ground for the study of the dissipation function \({\mathfrak {M}}_{0}^{\alpha }\).
In Sect. 4 we thoroughly establish the setup for our analysis, specifying the basic conditions on the spaces, on the energy functional, and on the dissipation potentials. Moreover, Theorem 4.8 recalls the existence result from [41] for the viscous system (1.4). Section 4.6 is devoted to the derivation of a priori estimates for the solutions \((u_\varepsilon ,z_\varepsilon )_\varepsilon \) to (1.4) that are uniform with respect to the parameter \(\varepsilon \).
Section 5.1 entirely revolves around the functional \({\mathfrak {M}}_{0}^{\alpha }\) that has a central role in the definition of both \(\text {pBV}\) and true \(\text {BV}\) solutions. In particular, (i) we motivate its definition as the Mosco limit of the family of the time-integrated dissipation functionals appearing in (1.8), and (ii) relying on the results from Sect. 3 we compute the limit \({\mathfrak {M}}_{0}^{\alpha }\) explicitly and investigate its properties. In the subsequent subsections we give the definition of parametrized Balanced-Viscosity solution to the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\), state our existence results in Theorem 5.12 (and Theorem 5.15 for enhanced \(\text {pBV}\) solutions), and present the characterizations of \(\text {pBV}\) solutions in terms of the subdifferential inclusions (1.13), cf. Theorem 5.21.
In Sect. 6 we introduce true \(\text {BV}\) solutions and state our existence result Theorem 6.8 (and Theorem 6.12 for enhanced BV solutions). In particular, we show that these solutions are obtained by taking the vanishing-viscosity limit in system (1.4) written in the real time variable \(t\in [0,T]\). We also gain further insight into the description of the jump dynamics provided by true \(\text {BV}\) solutions.
The proofs of the main results of Sects. 5 and 6 are carried out in Sect. 7.
Section 8 shows that our abstract setup is suitable to handle a concrete application to in solid mechanics. In particular, in Theorem 8.1 we prove the existence of enhanced parametrized and true \(\text {BV}\) solutions for a viscoelastic model with delamination along a prescribed interface.
1.6 General Notations
Throughout the paper, for a given Banach space X, we will denote its norm by \(\Vert \cdot \Vert _X\). For product spaces \(X {\times }\cdots {\times }X\), we will often (up to exceptions) simply write \(\Vert \cdot \Vert _X\) in place of \(\Vert \cdot \Vert _{X {{\times }\cdots {\times }}X}\). By  we shall denote both the duality pairing between X and \(X^*\) and the scalar product in X, if X is a Hilbert space.
we shall denote both the duality pairing between X and \(X^*\) and the scalar product in X, if X is a Hilbert space.
We shall use the symbols \(c,\,c',\, C,\,C'\), etc., whose meaning may vary even within the same line, to denote various positive constants depending only on known quantities. Furthermore, the symbols \(I_i\), \(i = 0, 1,\ldots \), will be used as place-holders for terms involved in the various estimates: we warn the reader that we will not be self-consistent with the numbering, so that, for instance, the symbol \(I_1\) will occur several times with different meanings.
2 A Prototypical Class of Coupled Systems
In this section we illustrate the notion of parametrized \(\text {BV}\) solution for a prototypical and simple class of coupled systems to which the existence and characterization results obtained in the sequel will apply. In particular, it contains a model combining linearized viscoelasticity and viscoplasticity. We shall confine the discussion to the particular case in which the ambient spaces
the viscous dissipation potentials are quadratic, namely,
with bounded linear, symmetric and positive definite operators \({\mathbb {V}}_{\textsf{x}}:{\textbf{X}}\rightarrow {\textbf{X}}^* \), and the driving energy functional is of the form

where \({\mathbb {A}}: {\textbf{U}}\rightarrow {\textbf{U}}^* \) and \({\mathbb {G}}: {\textbf{Z}}\rightarrow {\textbf{Z}}^*\) are linear, bounded and self-adjoint, \({\mathbb {B}}: {\textbf{U}}\rightarrow {\textbf{Z}}^*\) is linear and bounded, and \((f,g): [0,T]\rightarrow {\textbf{U}}^*{\times }{\textbf{Z}}^*\) are smooth time-dependent applied forces. Moreover, we assume that the block operator \(\left( {\begin{array}{c}{\mathbb {A}}\ {\mathbb {B}}^*\\ {\mathbb {B}}\ {\mathbb {G}}\end{array}}\right) \) is positive definite. Together with the 1-homogeneous potential \({{\mathcal {R}}}: {\textbf{Z}}\rightarrow [0,\infty )\) the viscous system (1.4) reads as
with \({\mathbb {V}}_{\textsf{x}}\) from (2.1b). It will be important to allow for coercivity of \({{\mathcal {R}}}\) on a Banach space \({\textbf{Z}}_{{\textrm{ri}}}\) such that \({\textbf{Z}}\subset {\textbf{Z}}_{{\textrm{ri}}}\) continuously and \({{\mathcal {R}}}(z')\ge c\Vert z'\Vert _{{\textbf{Z}}_{{\textrm{ri}}}}\) for all \(z'\in {\textbf{Z}}_{{\textrm{ri}}}\).
Example 2.1
(Linearized viscoelastoplasticity with hardening) Let the elastoplastic body occupy a bounded Lipschitz domain \(\Omega \subset {\mathbb {R}}^d\): linearized elastoplasticity is described in terms of the displacement \(u:\Omega \rightarrow {\mathbb {R}}^d\) with \(u\in {\textbf{U}}={\textrm{H}}^1_0(\Omega )\) for simplicity and in terms of the symmetric, trace-free plastic strain tensor \(z:\Omega \rightarrow {\mathbb {R}}_{{\textrm{dev}}}^{d{\times }d}:= \big \{{z\in {\mathbb {R}}_{{\textrm{sym}}}^{d{\times }d}}\, \big \vert {\, {\textrm{tr}}(z)=0}\big \}\). The driving energy functional \({{\mathcal {E}}}: [0,T]{\times }{\textbf{U}}{\times }{\textbf{Z}}\rightarrow {\mathbb {R}}\) with \({\textbf{Z}}= {\textrm{L}}^2(\Omega ; {\mathbb {R}}_{{\textrm{dev}}}^{d{\times }d})\) is defined by

with e(u) being the linearized symmetric strain tensor, \({\mathbb {C}} \in {\textrm{Lin}}({\mathbb {R}}_{\textrm{sym}}^{d{\times }d}) \) and \({\mathbb {H}}\in {\textrm{Lin}}({\mathbb {R}}_{\textrm{dev}}^{d{\times }d})\) are the positive definite and symmetric elasticity and hardening tensors, respectively, and \(f: [0,T]\rightarrow {\textrm{H}}^{-1}(\Omega ;{\mathbb {R}}^d)\) a time-dependent volume loading. The dissipation potentials are
where \(\sigma _{\textrm{yield}}>0\) is the yield stress and \({\mathbb {D}} \in {\textrm{Lin}}({\mathbb {R}}_{\textrm{sym}}^{d{\times }d})\) and \({\mathbb {V}} \in {\textrm{Lin}}({\mathbb {R}}_{\textrm{devm}}^{d{\times }d})\) are the symmetric and positive definite viscoelasticity and viscoplasticity tensors, respectively.
Hence, system (2.2) translates into
where “\({\textrm{dev}}\)” projects to the deviatoric part, namely \({\textrm{dev}}\,A = A - \frac{1}{d} ({\textrm{tr}}\!\; A)\,I\).
For the system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) from (2.1), featuring 2-positively homogeneous dissipation potentials, the time-space dissipation function \({\mathfrak {M}}_{0}^{\alpha }\) that enters into the definition of (parametrized) Balanced Viscosity solution can be explicitly computed (cf. Example 5.3 ahead). Nonetheless, here we can give an even more transparent illustration of (parametrized) \(\text {pBV}\) solutions in terms of their differential characterization (1.13). The upcoming Theorem 5.21 states that a triple \(({\textsf{t}},{\textsf{u}},{\textsf{z}})\) is an (enhanced) parametrized \(\text {BV}\) solution if and only if it solves, for almost all \(s\in (0,{{{\textsf{S}}}})\),
joint with the ‘switching conditions’ (1.13b)–(1.13c) on the measurable functions \(\lambda _{\textsf{u}}, \, \lambda _{\textsf{z}}: (0,{{{\textsf{S}}}})\rightarrow [0,\infty ]\). Here “\(\infty \mathbb V_{\textsf{z}}{{\textsf{z}}'}\,\)” has to be interpreted in the sense of \(\partial {{\mathcal {V}}}_{\textsf{z}}^{\infty }({\textsf{z}}')\), see (1.5b).
We recall that (1.13b) simply ensures that, if the system is not jumping (i.e., \({\textsf{t}}'(s)>0\)), then viscosity does not come into action, i.e. \(\lambda _{\textsf{u}}(s)=\lambda _{\textsf{z}}(s)=0\). This means that \({\textsf{u}}(s)\) is in ‘E’quilibrium with respect to \({\textsf{z}}(s)\) and the loading \(f({\textsf{t}}(s))\), whereas \({\textsf{z}}\) evolves according to the truly ‘R’ate-independent evolution \(\partial {{\mathcal {R}}}({\textsf{z}}')+{\mathbb {B}}{\textsf{u}}+ {\mathbb {G}}{\textsf{z}}\ni g\), hence we will denote this evolution regime by \({\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}}\) in Sect. 5.5.
Conditions (1.13c) differ in the three cases \(\alpha =1\), \(\alpha >1\) and \(\alpha \in (0,1)\) and indeed show how the (possibly different) relaxation rates of the variables u and z influence the system behavior at jumps, see Sect. 5.5 for a full discussion of the occurring evolution regimes.
For \(\underline{{\alpha =1}}\) the variables u and z relax with the same rate: at a jump, the system may switch to a viscous regime where the viscosity in u and in z are involved equally, since the coefficients \(\lambda _{\textsf{u}}\) and \(\lambda _{\textsf{z}}\) modulating the ‘V’iscosity terms \(\mathbb V_{\textsf{u}}{{\textsf{u}}'}\) and \({\mathbb {V}}_{\textsf{z}}{{\textsf{z}}'} \) coincide. This evolution regime will be denoted \({\textrm{V}}_{\textsf{uz}}\).
For \(\underline{{\alpha >1}}\) the switching condition (1.13c) imposes that either \(\lambda _{\textsf{z}} =\infty \) (i.e. \({\textsf{z}}'=0\)) or that \(\lambda _{\textsf{u}}=0\) (so that \({\textsf{u}}\) is at equilibrium). Indeed, since \({\textsf{u}}\) relaxes ‘V’iscously faster to equilibrium than \({\textsf{z}}\) to rate-independent evolution, \({\textsf{z}}\) is ‘B’locked until \({\textsf{u}}\) has reached the equilibrium: we call this evolution regime \({\textrm{V}}_{\textsf{u}} {\textrm{B}}_{\textsf{z}}\). After that \({\textsf{u}}\) is in ‘E’quilibrium and \({\textsf{z}}\) may have a ‘V’iscous transition with \(\lambda _{\textsf{z}}>0\), a regime denoted by \({\textrm{E}}_{\textsf{u}} {\textrm{V}}_{\textsf{z}}\). Moreover, under suitable conditions on the operators \({\mathbb {A}}\), \({\mathbb {B}}\), and \({\mathbb {G}}\) which in particular ensure that the functional \({\mathcal {E}}(t,\cdot , z)\) from (2.1c) is uniformly convex, the arguments from [43, Prop. 5.5] may be repeated for the system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) defined via (2.1). Hence, it is possible to show that the regime \({\textrm{V}}_{\textsf{u}} {\textrm{B}}_{\textsf{z}}\) can only occur once in the initial phase, while \({\textsf{u}}\) never leaves equilibrium afterwards, i.e. only \({\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}}\) and \({\textrm{E}}_{\textsf{u}} {\textrm{V}}_{\textsf{z}}\) are possible.
For \(\underline{{\alpha \in (0,1)}}\) the variable \({\textsf{z}}\) relaxes faster than \({\textsf{u}}\), which leads to the two viscous regimes: (i) \({\textrm{B}}_{\textsf{u}} {\textrm{V}}_{\textsf{z}}\) where \({\textsf{u}}\) is blocked (\(\lambda _{\textsf{u}}=\infty \)) while \({\textsf{z}}\) evolves viscously, and (ii) \({\textrm{V}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}}\) where \({\textsf{u}}\) relaxes to equilibrium while \({\textsf{z}}\) stays in locally stable states (\(\lambda _{\textsf{z}}=0\)). For \(\alpha \in (0,1)\) these two regimes and \({\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}}\) may occur more than once in the evolution of the system.
3 Some Auxiliary Tools for Dissipation Potentials
In this section we prepare a series of useful tools for handling the balanced effect of the different dissipation potentials; they will be essential for the upcoming analysis and may be interesting elsewhere.
Definition 3.1
(Primal and dual dissipation potentials) Let X be a reflexive Banach space. Then, a function \(\psi :X\rightarrow [0,\infty ]\) is called a (primal) dissipation potential, if
The dual dissipation potential \(\psi ^*:X^*\rightarrow [0,\infty ]\) is defined via Legendre–Fenchel conjugation as
Note that \(\psi ^*\) is indeed again a dissipation potential, and we have \((\psi ^*)^*=\psi \). In this section, we allow for functionals \(\psi \) taking the value \(\infty \) as well as degenerate functionals such that \(\psi (v)=0\) for \(v\ne 0\). With \(\psi \) we associate the B-function
We highlight the rescaling properties of \({\mathcal {B}}_\psi \) as
We will use that the functional \( {\mathcal {B}}_{\psi }(\cdot ,\cdot , \sigma )\) is convex for all \(\sigma \ge 0\). To see this, we consider \(\tau _0,\, \tau _1 \in (0,\infty )\), \(v_0,v_1 \in X\), and \(\theta \in [0,1]\) and set \(\tau _\theta : = (1{-}\theta )\tau _0+\theta \tau _1 >0\) and \(v_\theta : = (1{-}\theta )v_0+\theta v_1 \). With this we find that
where in \(\overset{(1)}{\le }\ \) we used the convexity of \(\psi \). We next define the functional
We shall refer to the functional \({\mathfrak {b}}_\psi \) as vanishing-viscosity contact potential associated with \(\psi \), in accordance with the terminology used in [39]. As we will see, \({\mathfrak {b}}_\psi \) will be handy for describing the interplay of vanishing viscosity and time rescaling upon taking the limit of (1.4).
3.1 Properties of Vanishing-Viscosity Contact Potentials \({\mathfrak {b}}_\psi \)
For arbitrary dissipation potentials \(\psi \), we define the rate-independent part \(\psi _{\textrm{ri}}:X \rightarrow [0,\infty ]\) via
The following results are slight variants of the results in [39, Thm. 3.7]:
Proposition 3.2
(Properties of vanishing-viscosity contact potentials) Assume that the dissipation potential \(\psi :X \rightarrow [0,\infty ]\) is superlinear, i.e.
Then, \({\mathfrak {b}}_\psi \) has the following properties:
-
(b1)
\({\mathfrak {b}}_\psi (v,\sigma )=0\) implies \(\sigma =0\) or \(v=0\). Moreover, \({\mathfrak {b}}_\psi (0,\sigma )=0\) for all \(\sigma \ge 0\).
-
(b2)
For all \(v\in X\) the function \({\mathfrak {b}}_\psi (v,\cdot ):[0,\infty ) \rightarrow [0,\infty ]\) is nondecreasing and concave. For \(v\ne 0\) and \(\sigma >0\) the infimum in the definition of \({\mathfrak {b}}_\psi \) is attained at a value \(\tau _{v,\sigma } \in (0,\infty )\). Moreover, for all \(v \ne 0 \) and \(\sigma >0\) we have \({\mathfrak {b}}_\psi (v,\sigma ) > {\mathfrak {b}}_\psi (v,0)=\psi _{\textrm{ri}}(v)\).
-
(b3)
For all \(\sigma \ge 0\) the function \({\mathfrak {b}}_\psi (\cdot ,\sigma ):X \rightarrow {[0,\infty )}\) is positively 1-homogeneous, lsc, and convex.
-
(b4)
If \(\psi = \phi +\varphi \) where \(\phi \) is 1-homogeneous, then \({\mathfrak {b}}_{\phi +\varphi }(v,\sigma )= \phi (v) + {\mathfrak {b}}_\varphi (v,\sigma )\).
-
(b5)
For all \((v,\eta )\in X{\times }X^*\) we have \( {\mathfrak {b}}_\psi (v,\psi ^*(\eta )) \ge \langle \eta ,v\rangle _X\).
Proof
The main observation is that the function \(g_{v,\sigma }: (0,\infty ) \ni \tau \mapsto \tau \psi (\frac{1}{\tau }v) + \tau \sigma \) is convex (cf. (3.3)) and takes only nonnegative values. For \(\sigma >0\) we have \(g_{v,\sigma }(\tau ) \rightarrow \infty \) for \( \tau \rightarrow \infty \), and for \(v\ne 0\) we have \(g_{v,\sigma }(\tau )\rightarrow \infty \) for \(\tau \rightarrow 0^+\) due to superlinearity of \(\psi \).
Part (b1): If \({\mathfrak {b}}_\psi (v,\sigma ) = \inf g_{v,\sigma }(\cdot )=0\), the infimum must either be realized for \(\tau \rightarrow 0^+\) or for \(\tau \rightarrow \infty \). In the first case, the value of \(\sigma \) does not matter, but the superlinearity of \(\psi \) gives \(\tau \psi (\frac{1}{\tau }v) \rightarrow \infty \), unless \(v=0\). In the second case we have \(\tau \sigma \rightarrow \infty \), unless \(\sigma =0\). The relation \({\mathfrak {b}}_\psi (0,\sigma )=0\) is obvious.
Part (b2): The first two statements follow because \({\mathfrak {b}}_\psi (v,\cdot )\) is the infimum of a family of functions that are increasing and concave in \(\sigma \). For \(v\ne 0\) and \(\sigma >0\) the minimum of \(g_{v,\sigma }(\tau )\) is achieved at a \(\tau _{v,\sigma } \in (0,\infty )\) as \(g_{v,\sigma }(\tau ) \rightarrow \infty \) on both sides (i.e., as \(\tau \rightarrow 0^+\) and \(\tau \rightarrow \infty \)). Thus, \({\mathfrak {b}}_\psi (v,\sigma )\ge {\mathfrak {b}}_\psi (v,0)+ \sigma \tau _{v,\sigma } >{\mathfrak {b}}_\psi (v,0)\) as desired. The relation \({\mathfrak {b}}_\psi (v,0) = \psi _{\textrm{ri}}(v)\) follows easily from the convexity of \(\psi \).
Part (b3): The positive 1-homogeneity \({\mathfrak {b}}_\psi (\gamma v, \sigma )=\gamma {\mathfrak {b}}_\psi (v,\sigma )\) for all \(\gamma >0\) follows by replacing \(\tau \) by \(\tau \gamma \). Convexity is obtained as follows. For fixed \(v_0,v_1\in X\), \(\theta \in (0,1)\), and \(\sigma \ge 0\), we choose \(\varepsilon >0\) and find \(\tau _0,\tau _1>0 \) such that for \(j\in \{0,1\}\) we have
Here we assumed without loss of generality \({\mathfrak {b}}_\psi (v_j,\sigma )<\infty \) since otherwise there is nothing to be shown. Now we set \(v_\theta = (1{-}\theta ) v_0 + \theta v_1 \) and \(\tau _\theta =(1{-}\theta ) \tau _0 + \theta \tau _1>0\). Using the convexity (3.3) of the functional \({\mathcal {B}}_{\psi }\left( \cdot ,\cdot ,\sigma \right) \), we obtain
with the last inequality due to (3.7). Since \(\varepsilon >0\) was arbitrary, this is the desired result.
To prove lower semicontinuity, we use the special way \({\mathfrak {b}}_\psi \) is constructed and that \(\psi \) is lsc. For all sequences \(v_j\rightarrow v_*\) and \(\sigma _j\rightarrow \sigma _*\) we have to show that
We may assume \(\alpha <\infty \) and \({\mathfrak {b}}_\psi (v_*,\sigma _*)>0\), since otherwise the desired estimate is trivial.
The case \(\sigma _*=0\) is simple, as we have
It remains to consider the case \(v_*\ne 0\) and \(\sigma _*>0\). Since \(\Vert v_j\Vert \ge \Vert v_*\Vert /2>0\) and \(\sigma _j\ge \sigma _*/2>0\) for sufficiently large j, we see that the optimal \(\tau _j=\tau _{v_j,\sigma _j}\) lie in a set \([1/M,M]\Subset (0,\infty )\). Thus, choosing a subsequence (not relabeled), we may assume \(\tau _j\rightarrow \tau _\circ \) and obtain lower semicontinuity by using \(\frac{1}{\tau _j}v_j \rightarrow \frac{1}{\tau _\circ }v_*\) as follows:
Part (b4): The formula for \({\mathfrak {b}}_{\phi +\varphi }\) follows from a direct calculation.
Part (b5): We have \(g_\tau ( v, \psi ^*(\eta )) = \tau \Big (\psi \big (\frac{1}{\tau }v\big ) + \psi ^*(\eta ) \Big ) \ge \tau \big (\langle \eta ,\frac{1}{\tau }v\rangle \big ) = \langle \eta ,v\rangle , \) and taking the infimum over \(\tau >0\) gives the result. Thus, Proposition 3.2 is proved.
\(\square \)
There is a canonical case in which \({\mathfrak {b}}_\psi \) can be given explicitly, namely the case that \({\mathfrak {b}}_\psi (v)\) only depends on the Banach-space norm \(\Vert v\Vert \). In this case we have an explicit expression for \({\mathfrak {b}}_\psi \) and the functional \( X \times X^* \ni (v,\eta ) \mapsto {\mathfrak {b}}_\psi (v,\psi ^*(\eta ))\).
Lemma 3.3
(Dissipation potentials depending on the norm) Assume that \(\psi \) is given in the form \(\psi (v)=\zeta (\Vert v\Vert )\), where \(\zeta :[0,\infty )\rightarrow [0,\infty ]\) satisfies \(\zeta (0)=0\) and is lsc, nondecreasing, convex, and superlinear. Setting \(\zeta '(0)= \lim _{h\rightarrow 0^+} \frac{1}{h} \zeta (h)\) we have the identities
Proof
The first statement is trivial for \(v=0\). For \(v\ne 0\) we can replace \(\tau \) by \(\tau \Vert v\Vert \) and obtain the desired product form with \(\Vert v\Vert \) as the first factor.
To obtain the second statement in (3.8) we first observe that \(\psi ^*(\xi )=\zeta ^*(\Vert \xi \Vert _*)\) with \(\zeta ^*(r)=\sup \left\{ \, r\rho -\zeta (\rho )\, \big | \, \rho \ge 0 \,\right\} \). As \(\zeta \) is superlinear \(\zeta ^*(r)\) is finite for all \(r\ge 0\), and \(\zeta ^*(r)=0\) for \(r\in [0,\zeta '(0)]\). Secondly, we characterize \(\kappa _\zeta \) by using the following estimate
The inequality is even an identity if the infimum is attained, which is the case of \(\frac{1}{\tau }\in \partial \zeta ^*(r)\) for some \(\tau \). Thus, we have attainment whenever \(\zeta ^*(r)>0\), whereas for \(r\in [0,\zeta '(0)]\), where \(\zeta ^*(r)=0\), we have non-attainment but find \(\kappa _\zeta (0)= \zeta '(0)\). Together we arrive at \(\kappa _\zeta (\zeta ^*(r))= \max \{\zeta '(0),r\}\) (see also [27, Sec. 2.3]), and \( {\mathfrak {b}}( v,\psi ^*(\xi ))=\Vert v\Vert \kappa _\zeta (\zeta ^*(\Vert \xi \Vert _*))\) gives the desired result. \(\square \)
The above result shows that the estimate \({\mathfrak {b}}_\psi ( v,\psi ^*(\xi )) \ge \langle \xi ,v\rangle \) in (b4) improves to
with \(c_X=1\) in certain cases, in particular in the metric approach used in [38, 51]. Moreover, also in view of [44], it is worthwhile mentioning the weaker quantitative Young estimate
and its sharp version
Clearly, if the dissipation potential \(\psi \) only depends on the norm, then it satisfies (3.11) with \({\bar{c}}_\psi =1\). In turn, it is immediate to check that (3.11) provides (3.9) with \(c_X={\bar{c}}_\psi \). Further insight on (3.10) and (3.11) can be gained from the following:
Example 3.4
In \(X={\mathbb {R}}^2\), endowed with the Euclidean norm, we consider \(\psi (v)=\frac{1}{2}v_1^2+\phi (v_2)\) with a general continuous and convex \(\phi :{\mathbb {R}}\rightarrow {[0,\infty )}\) satisfying \(\phi (0)=0\). Assuming that (3.10) holds, we find that
Subtracting \(\frac{1}{2}w^2\) from the left-hand and the right-hand side and taking the supremum over w we obtain the lower bound \(\phi ^*(\zeta ) \ge \frac{1}{2} {{\bar{c}}}_\psi ^2 \zeta ^2 - {{\bar{C}}}_\psi \). With the similar estimate for \(\psi (w) + \frac{1}{2} \zeta ^2=\psi (0,w)+ \psi ^*(\zeta ,0)\) we see that (3.10) implies the lower and upper bounds
Moreover, these bound also imply (3.10), if we replace \({{\bar{c}}}_\psi \) and \({{\bar{C}}}_\psi \) by \({{\bar{c}}}_\psi ^2\) and \(2 {{\bar{C}}}_\psi \), respectively.
Furthermore, we see that the sharper estimate (3.11) (i.e. \(\bar{C}_\psi =0\)) can only hold if \(\frac{1}{2} {{\bar{c}}}_\psi ^2 w^2 \le \psi (w) \le 1/(2{{\bar{c}}}_\psi ^2)\, w^2\). In particular, we see that the choice \(\phi (w)=|w| + \frac{1}{2} w^2\) is compatible with (3.10), but not with the sharp quantitative Young estimate (3.11).
Let us return to (3.9): as some of the following examples show, the latter estimate is not true in general, and that is why we will derive general lower bounds on the vanishing-viscosity contact potential \({\mathfrak {b}}_\psi \) in Sect. 3.3.
Example 3.5
(The function \({\mathfrak {b}}_\psi \) for some special cases) The following cases give some intuition about the vanishing-viscosity contact potential \({\mathfrak {b}}_\psi \).
-
(A)
Assume that \(\psi \) is positively p-homogeneous with \(p\in (1,\infty )\), i.e. \(\psi (\gamma v) = \gamma ^p \psi (v)\) for all \(\gamma >0\) and \(v\in X\). Then, we have
$$\begin{aligned} {\mathfrak {b}}_\psi (v,\sigma )= & {} \big (\psi (v)\big )^{1/p}\, {\hat{c}}_p\, \sigma ^{1/p'}, \quad \text {where} \nonumber \\ {\hat{c}}_p= & {} p^{1/p} (p')^{1/p'}\quad \text {and}\quad \frac{1}{p}+\frac{1}{p'} =1. \end{aligned}$$(3.12)In particular, for \(\psi (v) = \frac{1}{p} \Vert v\Vert ^p\) we find
$$\begin{aligned} {\mathfrak {b}}_\psi (v,\sigma ) = \Vert v\Vert \big (p'\sigma \big )^{1/p'} \quad \text {and}\quad {\mathfrak {b}}_\psi (v,\psi ^*(\eta )) = \Vert v\Vert \Vert \eta \Vert _*. \end{aligned}$$ -
(B)
On \(X={\mathbb {R}}^2\) consider \(\psi (v)=\frac{1}{2}(av_1^2+b v_2^2)\) with \(a,b>0\). Then,
$$\begin{aligned} {\mathfrak {b}}_\psi (v,\sigma )= & {} \big (av_1^2{+}b v_2^2\big )^{1/2} \,(2\sigma )^{1/2} \quad \text {and}\\ {\mathfrak {b}}_\psi (v,\psi ^*(\xi ))= & {} \big (av_1^2{+}b v_2^2\big )^{1/2}\left( \frac{1}{a} \xi _1^2{+}\frac{1}{b} \xi _2^2\right) ^{1/2}. \end{aligned}$$If \({\mathbb {R}}^2\) is equipped with the Euclidean norm \(\Vert \cdot \Vert \), then \( {\mathfrak {b}}_\psi (v,\psi ^*(\xi )) \ge \big (\frac{\min \{a,b\}}{\max \{a,b\}}\big )^{1/2} \Vert \xi \Vert _* \Vert v\Vert \), but estimate (3.9) fails, while \( {\mathfrak {b}}_\psi (v,\psi ^*(\xi )) \ge \langle \xi , v \rangle \) obviously holds.
-
(C)
We still look at the case \(X={\mathbb {R}}^2\) with the Euclidean norm \(\Vert v\Vert =\big (v_1^2{+} v_2^2 \big )^{1/2}\) and
$$\begin{aligned} \psi (v)=\frac{1}{2}\, v_1^2 + \frac{1}{4} \, v_2^4 \quad \text {and} \quad \psi ^*(\xi )=\frac{1}{2}\, \xi _1^2 + \frac{4}{3} \, |\xi _2|^{4/3}. \end{aligned}$$In principle, we can calculate \({\mathfrak {b}}_\psi (v_1,v_2,\sigma )\) explicitly, however, it suffices to use (A) giving
$$\begin{aligned} {\mathfrak {b}}_\psi (v_1,0,\sigma )= |v_1|(2\sigma )^{1/2} \quad \text {and} \quad {\mathfrak {b}}_\psi (0,v_2,\sigma ) = |v_2| \big (\tfrac{4}{3} \sigma \big )^{3/4}. \end{aligned}$$Inserting \(\sigma =\psi ^*(\xi _1,\xi _2)\) and inserting the “wrong directions” with \(\langle \xi , v \rangle =0\) we find
$$\begin{aligned} {\mathfrak {b}}_\psi (v_1,0, \psi ^*(\xi _1,\xi _2))&= \big (\tfrac{8}{3}\big )^{1/2} |v_1|\,|\xi _2|^{2/3} \quad \text {and}\\ {\mathfrak {b}}_\psi (0,v_2, \psi ^*(\xi _1,\xi _2))&= \big (\tfrac{2}{3}\big )^{3/4} |v_2|\,|\xi _1|^{3/2}. \end{aligned}$$Clearly, there cannot be a constant \(c_0>0\) such that \( {\mathfrak {b}}_\psi (v,\psi ^*(\xi )) \ge c_0 \Vert v\Vert \, \Vert \xi \Vert \) for all \(v,\xi \in {\mathbb {R}}^2\). Of course, the relations are compatible with (b4) in Proposition 3.2, i.e. \( {\mathfrak {b}}_\psi (v,\psi ^*(\xi )) \ge \langle \xi , v \rangle \). Using \(v=(w,0)\) and \(\xi =(0,\zeta )\) and arguing as for Example 3.4 we also see that (3.10) does not hold.
As we will see, the vanishing-viscosity contact potentials \({\mathfrak {b}}_\psi \), which were developed for the case of two-rate problems (with time scales 1 and \(\varepsilon \)) in [39], are also relevant to describe the limiting behavior of B-functions in the multi-rate case with time scales 1, \(\varepsilon \), and \(\varepsilon ^\alpha \). For this, we will use the concept of (sequential) Mosco convergence, which we recall here for a sequence of functionals \({\mathscr {F}}_n: X\rightarrow (-\infty ,+\infty ] \) defined in a Banach space \(X\).
Definition 3.6
(Mosco convergence) We say that \({\mathscr {F}}: {X} \rightarrow (-\infty ,+\infty ] \) is the Mosco limit of the functionals \(({\mathscr {F}}_n)_n\) as \(n\rightarrow \infty \), and write \( {\mathscr {F}}_n \overset{{\textrm{M}}}{\rightarrow }{\mathscr {F}}\) in X, if the following two conditions hold:
3.2 Mosco Convergence for the Joint B-Functions \({\mathfrak {B}}_\varepsilon ^\alpha \)
In view of the vanishing-viscosity analysis of (1.4), we now work with two dissipation potentials \(\psi _{\textsf{u}}:{\textbf{U}}\rightarrow [0,\infty ]\) and \(\psi _{\textsf{z}}:{\textbf{Z}}\rightarrow [0,\infty ]\), with \({\textbf{U}}\) and \({\textbf{Z}}\) the state spaces from (1.1). In Sect. 5.1, we will indeed confine the discussion to the choices \(\psi _{\textsf{u}}: = {{\mathcal {V}}}_{\textsf{u}}\) and \(\psi _{{\textsf{z}}}: = {{\mathcal {R}}}+{{\mathcal {V}}}_{\textsf{z}}\), but here we want to keep the discussion more general and in particular allow for \(\psi _{\textsf{u}}\) to have a nontrivial rate-independent part, too.
When constructing the associated B-function we have to take care of the different scalings namely \(\psi _{\textsf{u}}^{\varepsilon ^\alpha }\) and \(\psi _{\textsf{z}}^\varepsilon \) in the sense of (1.5a), i.e. \(\psi ^\lambda (v)=\frac{1}{\lambda }\psi (\lambda v)\). Indeed, since the conjugate function \((\psi ^\lambda )^*\) satisfies the simple scaling law \(( \psi ^\lambda )^*(\xi )= \frac{1}{\lambda }\psi ^*(\xi )\), the B-function \({\mathcal {B}}_{\psi ^\lambda }\) obeys the scaling relations
where we used (3.2) for the last step. Our definition of the associated B-function for the sum
will be denoted by the symbol \({\mathfrak {B}}_{\Psi _{\varepsilon ,\alpha }}\), see (3.15) below. We emphasize that we deviate from the construction set forth in (3.1), since (3.15) applies (3.14) for each component individually. Hence, we introduce
Subsequently, we will use the short-hand notation \({\mathfrak {B}}_\varepsilon ^\alpha \) in place of \({\mathfrak {B}}_{\Psi _{\varepsilon ,\alpha }}\) and extend \({\mathfrak {B}}_\varepsilon ^\alpha \) to allow for the value \(\tau =0\), defining the rescaled joint B-function \({\mathfrak {B}}_\varepsilon ^\alpha :[0,\infty ){\times }{\textbf{U}}{\times }{\textbf{Z}}{\times }[0,\infty )^2\rightarrow [0,\infty ]\) via
We highlight that \({\mathfrak {B}}_\varepsilon ^\alpha \) is relevant for the coupled system (1.4), hence the name rescaled joint B-function.
The next result shows that the Mosco limit \({\mathfrak {B}}^\alpha _0\) of the B-functions \(({\mathfrak {B}}_\varepsilon ^\alpha )_\varepsilon \) always exists and can be expressed in terms of the potentials \({\mathfrak {b}}_{\psi _{\textsf{u}}}\), \({\mathfrak {b}}_{\psi _{\textsf{z}}}\), and \({\mathfrak {b}}_{\psi _{\textsf{u}}{\oplus }\psi _{\textsf{z}}}\). We emphasize that \((\tau ,u',z')\mapsto {\mathfrak {B}}^\alpha _0(\tau ,u',z',\sigma _{\textsf{u}},\sigma _{\textsf{z}})\) is 1-homogeneous, which reflects the rate-independent character of the limiting procedure.
Proposition 3.7
(Mosco limit \({\mathfrak {B}}^\alpha _0\) of the family \({\mathfrak {B}}^\alpha _\varepsilon \)) Let \(\psi _{\textsf{u}}\) and \(\psi _{\textsf{z}}\) satisfy (3.6) and assume \(\alpha >0\). Then, the family \({({\mathfrak {B}}^\alpha _\varepsilon )}_{\varepsilon >0}\) Mosco converges to the limit \({\mathfrak {B}}^\alpha _0:[0,\infty ){\times }{\textbf{U}}{\times }{\textbf{Z}}{\times }[0,\infty )^2\rightarrow [0,\infty ]\) that is given as follows:
where \(\psi :\quad = \psi _{\textsf{u}}\oplus \psi _{\textsf{z}}:(u',z')\mapsto \psi _{\textsf{u}}(u') {+} \psi _{\textsf{z}}(z')\). Thus, the functional \({\mathfrak {B}}_{0}^{\alpha }\left( \cdot ,\cdot ,\cdot , \sigma _{\textsf{u}}, \sigma _{\textsf{z}}\right) \) is convex and 1-homogeneous for all \((\sigma _{\textsf{u}}, \sigma _{\textsf{z}}) \in [0,\infty )^2\).
Proof
\(\underline{\text {Case }\tau >0.}\) Using \(\psi _{\textsf{x}}(v)\ge \big (\psi _{\textsf{x}}\big )_{\textrm{ri}} (v)\) we have
which easily provides the desired liminf estimate. The limsup estimate follows with the constant recovery sequence \((u'_\varepsilon ,z'_\varepsilon ,\sigma _{\textsf{u}, \varepsilon },\sigma _{\textsf{z}, \varepsilon })=(u',z',\sigma _{\textsf{u}},\sigma _{\textsf{z}})\).
\(\underline{\text {Case }\tau =0\text { and }\alpha =1.}\) By definition of \({\mathfrak {b}}_\psi = {\mathfrak {b}}_{\psi _{\textsf{u}}{\oplus } \psi _{\textsf{z}}}\) we have
Hence, the liminf estimate follows from Proposition 3.2.
For the limsup estimate for \({\mathfrak {B}}_{0}^{1}\left( 0,u',z', \sigma _{\textsf{u}}, \sigma _{\textsf{z}}\right) \) we choose \(\lambda _\varepsilon \) such that \(\lambda _\varepsilon \psi (\frac{1}{\lambda _\varepsilon } (u',z')) + \lambda _\varepsilon (\sigma _{\textsf{u}}{+}\sigma _{\textsf{z}}) \rightarrow {\mathfrak {b}}_\psi ((u',z'),\sigma _{\textsf{u}}{+}\sigma _{\textsf{z}})\), where we may assume \(\lambda _\varepsilon \le 1/\sqrt{\varepsilon }\). Then, it suffices to set \(\tau _\varepsilon = \lambda _\varepsilon \varepsilon \rightarrow 0\) to conclude \({\mathfrak {B}}_{\varepsilon }^{1}\left( \tau ,u',z', \sigma _{\textsf{u}}, \sigma _{\textsf{z}}\right) \rightarrow {\mathfrak {b}}_\psi ((u',z'),\sigma _{\textsf{u}}{+}\sigma _{\textsf{z}})= {\mathfrak {B}}_{0}^{1}\left( 0,u',z', \sigma _{\textsf{u}}, \sigma _{\textsf{z}}\right) \).
\(\underline{\text {Case }\tau =0\text { and }\alpha >1.}\) For the lower bound in the liminf estimate we only need to consider the case \(\sigma _{\textsf{u}}=0\) and the case \(\sigma _{\textsf{u}}>0\) and \(z'=0\). In the latter situation we may drop the two last terms in the definition of \({\mathfrak {B}}^\alpha _\varepsilon \) and the lower bound is established by the lower semicontinuity of \({\mathfrak {b}}_{\psi _{\textsf{u}}}\). In the case \(\sigma _{\textsf{u}}=0\), we have the lower bound
and the liminf again follows by the lsc.
For the limsup estimates we use the recovery sequence \((\tau _\varepsilon ,u',z',\sigma _{\textsf{u}},\sigma _{\textsf{z}})\) converging strongly with \(\tau _\varepsilon \rightarrow 0\), as in the previous case. For \(\sigma =0\) we choose \(\tau _\varepsilon =\lambda _\varepsilon \varepsilon \) where \(\lambda _\varepsilon \) realizes the infimum in \({\mathfrak {b}}_{\psi _{\textsf{z}}}(z',\sigma _{\textsf{z}})\). In the case \(\sigma _{\textsf{u}}>0\) and \(z'=0\) we choose \(\tau _\varepsilon = {\hat{\lambda }}_\varepsilon \varepsilon ^\alpha \), where \({\hat{\lambda }}_\varepsilon \) realizes the infimum in \( {\mathfrak {b}}_{\psi _{\textsf{u}}}(u',\sigma )\). In the remaining case, which has \(\sigma >0\), we may choose \(\tau _\varepsilon =\varepsilon \).
\(\underline{\text {Case }\tau =0\text { and }\alpha <1.}\) This case is similar to the case \(\alpha >1\) if we interchange the role of \(u'\) and \(z'\). Thus, Proposition 3.7 is proved. \(\square \)
3.3 Lower Bounds for the B-Function \({\mathfrak {B}}_\varepsilon ^\alpha \)
In the subsequent convergence analysis for the vanishing-viscosity limit we will need \(\varepsilon \)-uniform a priori bounds for the time derivatives of the solutions \(q_\varepsilon =(u_\varepsilon ,z_\varepsilon )\). They are derived by lower bounds for the B-functions, however, we have already observed in Example 3.5 that the simple lower bound \({\mathfrak {b}}_\psi (v,\psi ^*(\xi ))\ge \Vert \xi \Vert _*\Vert v\Vert \) in (3.9) cannot be expected. The following result provides suitable surrogates of such estimate. They will play a crucial role in the vanishing-viscosity analysis, specifically in controlling \(\Vert z'\Vert \) along jump paths, see Lemma 5.4. For this it will be important that the function \(\varkappa \) occurring in (3.17) is strictly increasing, which implies \(\varkappa (\sigma )>0\) for \(\sigma >0\).
Lemma 3.8
(Lower bound on \({\mathfrak {B}}^\alpha _\varepsilon \)) Let \(\psi _{\textsf{u}}\) and \(\psi _{\textsf{z}}\) satisfy (3.6) and let \({\mathfrak {B}}^\alpha _\varepsilon \) be given as in (3.16). Then, there exists a continuous, convex, nondecreasing, and superlinear function \(\varphi : [0,\infty )\rightarrow [0,\infty )\) such that
where \(\varkappa \in {\textrm{C}}([0,\infty );[0,\infty ))\) is given by \(\varkappa (\sigma )= (\varphi ^*)^{-1}(\sigma )\), is concave, and strictly increasing with \(\varkappa (0)=0\) and \(\varkappa (\sigma )\rightarrow \infty \) for \(\sigma \rightarrow \infty \). We additionally have
Proof
\(\underline{\textit{Step 1: Construction of}\,\varphi .}\) Since \(\psi _{\textsf{u}}\) and \(\psi _{\textsf{z}}\) are superlinear, for each \(K\ge 0\) there exists \(S_K\ge 0\) such that
Hence, the estimates in (3.17a) hold for the nonnegative, convex function \(\varphi \) given by
From \(\varphi (0)=0\) and non-negativity we conclude that \(\varphi \) is nondecreasing. Moreover, it is superlinear by construction.
\(\underline{\textit{Step 2: Lower bound on }{\mathfrak {b}}_{\psi _{\textsf{x}}}.}\) In the definition of \({\mathfrak {b}}_\psi \) the dependence on \(\psi \) is monotone (because of \(\tau >0\)) so that \(\psi _1\le \psi _2\) implies \({\mathfrak {b}}_{\psi _1} \le {\mathfrak {b}}_{\psi _2}\). Setting \({\widetilde{\varphi }}(v)=\varphi (\Vert v\Vert )\) we obtain \({\mathfrak {b}}_{\psi _{\textsf{x}}}\ge {\mathfrak {b}}_{{\widetilde{\varphi }}}\), and using Lemma 3.3 and the definition of \(\varkappa \) yields
\(\underline{\textit{Step 3: Lower bound on }{\mathfrak {B}}^\alpha _\varepsilon .}\) The definitions of \({\mathfrak {B}}^\alpha _\varepsilon \) in (3.15b) and of \({\mathfrak {b}}_\psi \) give, for \(\varepsilon >0\),
where Step 2 was invoked for the last estimate. This proves (3.17b).
Estimate (3.17d) follows from the simple observation that, because of \(\alpha =1\), the rescaled B-function \({\mathfrak {B}}^1_\varepsilon \) only depends \(\sigma _{\textsf{u}} {+}\sigma _{\textsf{z}}\), such that each of \(\sigma _{\textsf{u}}\) and \(\sigma _{\textsf{z}}\) can be replaced by their arithmetic mean.
For \(\alpha \ge 1\) and \(\varepsilon \in (0,1]\), we have \(\tau /{\varepsilon ^\alpha } \ge \tau /\varepsilon \) so that
This shows estimate (3.17e), and (3.17c) follows similarly.
All estimates remain true for \(\varepsilon =0\) because \({\mathfrak {B}}^\alpha _0\) is the Mosco limit of \({\mathfrak {B}}^\alpha _\varepsilon \). \(\square \)
4 Setup and Existence for the Viscous System
In Sect. 4.1 we will introduce our basic conditions on the ambient spaces, the energy, and the dissipation potentials, collected in Hypotheses 4.1, 4.2, 4.3, and 4.5, which will be assumed throughout the paper. Let us mention in advance that we will often omit to explicitly recall these assumptions in the various intermediate statements, with the exception of our main results in Theorems 5.12, 5.15, 6.8, and 6.12.
Then, in Sect. 4.4 we will address the existence of solutions to the viscous system (1.4). Its main result, Theorem 4.8, shows that, under two additional conditions on the driving energy functional, the existence result from [41, Thm. 2.2] can be applied to deduce the existence of solutions for the doubly nonlinear system (1.4). It will be crucial to our analysis that we are able to show that these solutions satisfy the \((\Psi ,\Psi ^*)\) energy-dissipation balance (1.8).
4.1 Function Spaces
Here we state our standing assumptions on the function spaces for the energy functionals and for the dissipation potentials.
Hypothesis 4.1
(Function spaces) In addition to conditions (1.1) on the ambient spaces \({\textbf{U}}\) and \({\textbf{Z}}\), our (coercivity) conditions on the energy \({{\mathcal {E}}}\) will involve two other reflexive spaces \({\textbf{U}}_{{\textrm{e}}}\) and \({\textbf{Z}}_{{\textrm{e}}}\), such that
Furthermore, the 1-homogeneous dissipation potential \({{\mathcal {R}}}\), defined on \({\textbf{Z}}\), will be in fact coercive with respect to the norm of a (separable) space \({\textbf{Z}}_{{\textrm{ri}}}\) (where the subscript \({\textrm{ri}}\) accordingly refers to rate-independence), such that
The subscript \({\textrm{e}}\) in the notation \({\textbf{U}}_{{\textrm{e}}}\), \({\textbf{Z}}_{{\textrm{e}}}\) refers to the fact that the latter are ‘energy spaces’ relating to \({{\mathcal {E}}}\); see Hypothesis 4.3 later on.
We refer to (4.9) for some examples of relevant ambient spaces. In what follows, we will often use the notation
4.2 Assumption on the Dissipation Potentials
We will develop the general theory under the condition that the viscous dissipation potentials \({{\mathcal {V}}}_{\textsf{u}}\) and \({{\mathcal {V}}}_{\textsf{z}}\) as well as the 1-homogeneous potential \({{\mathcal {R}}}\) take only finite values in \([0,\infty )\) and are thus continuous. Recall that \({{\mathcal {V}}}_{\textsf{x}}^*\) is the Legendre–Fenchel conjugate of \({{\mathcal {V}}}_{\textsf{x}}\), see Definition 3.1.
Hypothesis 4.2
(Conditions on \({{\mathcal {V}}}_{\textsf{u}}\), \({{\mathcal {V}}}_{\textsf{z}}\), \({{\mathcal {R}}}\)) Let \({{\mathcal {V}}}_{\textsf{u}}: {\textbf{U}}\rightarrow [0,\infty )\) and \({{\mathcal {V}}}_{\textsf{z}}: {\textbf{Z}}\rightarrow [0,\infty )\) be dissipation potentials with the following additional conditions:
Let \({{\mathcal {R}}}: {\textbf{Z}}\rightarrow [0,\infty ]\) be a 1-homogeneous dissipation potential, i.e.
that is additionally \({\textbf{Z}}\)-bounded and \({\textbf{Z}}_{{\textrm{ri}}}\)-coercive, i.e.
Due to the superlinear growth of \({{\mathcal {V}}}_{\textsf{x}}\) and \({{\mathcal {V}}}_{\textsf{x}}^*\), \({\textsf{x}}\in \{ {\textsf{u}}, {\textsf{z}}\}, \) these potentials are also bounded on bounded sets (as lower bounds imply upper bounds for the Legendre dual). By convexity and boundedness we then obtain Lipschitz continuity on all bounded sets. Likewise, \({{\mathcal {R}}}\) is continuous. Indeed, restricting our analysis to the case in which \({{\mathcal {R}}}\) takes only finite values in \([0,\infty )\) excludes the direct application of our results to systems modeling unidirectional processes in solids such as damage or delamination. In those cases the existence theory (both for the rate-dependent, ‘viscous’ system and for \(\text {BV}\) solutions of the rate-independent process) relies on additional estimates not considered here, see e.g. [24]. Nevertheless, a broad class of models is still described by continuous dissipation functionals. For instance, the coercivity and growth conditions (4.3b) are compatible with the following example of dissipation potential, in the ambient space \({\textbf{Z}}={\textrm{L}}^2(\Omega )\) and with \({\textbf{Z}}_{{\textrm{ri}}}={\textrm{L}}^1(\Omega )\) (with \(\Omega \subset {\mathbb {R}}^d\) a bounded domain and \(\delta _+,\delta _->0\)):
Dissipation potentials with this structure occur, for instance, in models for damage or delamination allowing for possible healing, cf. e.g. [33, Sec. 5.2.7] and Sect. 8.
Subsequently, \(\partial {{\mathcal {R}}}: {\textbf{Z}}\rightrightarrows {\textbf{Z}}^*\) will denote the convex subdifferential \({{\mathcal {R}}}\). By the 1-homogeneity (4.3a) we have

As a consequence of (4.3b), we have
4.3 Assumptions on the Energy \({{\mathcal {E}}}\)
We now collect our basic requirements on the energy functional \({{\mathcal {E}}}: [0,T]{\times }{\textbf{U}}{\times } {\textbf{Z}}\rightarrow (-\infty ,\infty ]\). With slight abuse of notation, we will often write \({{\mathcal {E}}}(t,q) \) in place of \( {\mathcal {E}}(t,u, z)\), in accordance with (4.1). Recall the embeddings \({\textbf{U}}_{{\textrm{e}}}\subset {\textbf{U}}\) and \({\textbf{Z}}_{{\textrm{e}}}\Subset {\textbf{Z}}\subset {\textbf{Z}}_{{\textrm{ri}}}\) and the choice \({\textbf{Q}}= {\textbf{U}}{\times }{\textbf{Z}}\).
Hypothesis 4.3
(Lower semicontinuity, coercivity, time differentiability of \({{\mathcal {E}}}\)) The energy functional \({{\mathcal {E}}}: [0,T]{\times }{\textbf{U}}{\times }{\textbf{Z}}\rightarrow (-\infty ,\infty ]\) has the proper domain \({\textrm{dom}}({{\mathcal {E}}}) = [0,T]{\times }{\mathscr {D}}\) with \({\mathscr {D}}\subset {\textbf{U}}_{{\textrm{e}}}{\times }{\textbf{Z}}_{{\textrm{e}}}\). Moreover, we require that
and \({{\mathcal {E}}}\) is bounded from below:
We set \({\mathfrak {E}}( q):= \sup _{t\in [0,T]} {\mathcal {E}}(t,q) \) and require that
Finally, we require that \(t \mapsto {\mathcal {E}}(t,q)\) is differentiable for all \(q\in {\mathscr {D}}\) satisfying the power-control estimate
Concerning our conditions on \({\textrm{dom}}({{\mathcal {E}}})\), the crucial requirement is that \({\textrm{dom}}({{\mathcal {E}}}(t,\cdot )) \equiv {\mathscr {D}}\) is independent of time. Let us introduce the energy sublevels
Applying Grönwall’s lemma we deduce from (4.7d) that
Hence, \({{\mathcal {E}}}(t,q) \le E\) for some \(t\in [0,T]\) and \(E>0\) guarantees \(q\in {\mathcal {S}}_{E'}\) with \(E' = {\textrm{e}}^{C_\# T} \, E \). Finally, observe that (4.7c) implies the separate coercivity properties of the functionals \({\mathfrak {E}}(\cdot ,z)\) and \({\mathfrak {E}}( u,\cdot )\), perturbed by the norm \(\Vert \cdot \Vert _{\textbf{U}}\) and \(\Vert \cdot \Vert _{{\textbf{Z}}_{{\textrm{ri}}}}\), respectively.
Since we are only requiring that \({\textbf{U}}_{{\textrm{e}}}\subset {\textbf{U}}\) continuously, our analysis allows for the following two cases: (i) the energy \({\mathcal {E}}(t,\cdot , z)\) and the dissipation potential \({{\mathcal {V}}}_{\textsf{u}}\) have sublevels bounded in the same space and (ii) the energy \({\mathcal {E}}(t,\cdot , z)\) has sublevels compact in the space \({\textbf{U}}\) of the dissipation \({{\mathcal {V}}}_{\textsf{u}}\). To fix ideas, typical examples for the pairs \(({\textbf{U}},{\textbf{U}}_{{\textrm{e}}})\) and the triples \(({\textbf{Z}}_{{\textrm{e}}}, {\textbf{Z}},{\textbf{Z}}_{{\textrm{ri}}})\) are
As mentioned in the introduction, in our analysis we aim to allow for nonsmoothness of the energy functional \(q=(u,z)\mapsto {\mathcal {E}}(t,q)\). Accordingly, we will use the Fréchet subdifferential of \({{\mathcal {E}}}\) with respect to the variable q, i.e. the multivalued operator \(\partial _{\textsf{q}}{{\mathcal {E}}}: [0,T] {\times }{\textbf{Q}}\rightrightarrows {\textbf{Q}}^*\) defined for \((t,q)\in [0,T]{\times }{\mathscr {D}}\) via

with domain \({\textrm{dom}}(\partial _{\textsf{q}}{{\mathcal {E}}}): = \left\{ \, (t,q) \in [0,T] {\times }{\mathscr {D}}\, \big | \, \partial _{\textsf{q}}{{\mathcal {E}}}(t,q) \ne \varnothing \,\right\} \).
Thus, our aim is to solve the subdifferential inclusion
where the scaled dissipation potential \(\Psi _{\varepsilon ,\alpha } \) is defined in (1.7).
Remark 4.4
(Partial Fréchet subdifferentials) Observe that
where \(\partial _{\textsf{u}}{{\mathcal {E}}}(t,q)\subset {\textbf{U}}^*\) and \(\partial _{\textsf{z}}{{\mathcal {E}}}(t,q)\subset {\textbf{Z}}^*\) are the ‘partial’ Fréchet subdifferentials of \({{\mathcal {E}}}\) with respect to the variables u and z, which are defined as Fréchet subdifferentials of \({\mathcal {E}}(t,\cdot , z):{\textbf{U}}\rightarrow {\mathbb {R}}\) and \({\mathcal {E}}(t,u, \cdot ):{\textbf{Z}}\rightarrow {\mathbb {R}}\), respectively. However, equality in (4.12) is false, in general, e.g. for \({\textbf{U}}={\textbf{Z}}={\mathbb {R}}\) and \({{\mathcal {E}}}(t,u,z)=|u{-}z|\).
In view of the inclusion (4.12), any curve \(t \mapsto q(t)=(u(t),z(t))\) solving (4.11) also solves the system
Nonetheless, let us stress that the ‘reference viscous system’ for the subsequent discussion will be the one with the smaller solution set, namely (4.11) or (4.18a) below.
The existence result from [41] can be applied provided that \({{\mathcal {E}}}\) fulfills two further conditions, stated in the following Hypotheses 4.5 and 4.7.
Hypothesis 4.5
(Closedness of \((\partial _q{{\mathcal {E}}},\partial _t{{\mathcal {E}}})\) on sublevels) For all sequences \(\big ((t_n,q_n, \xi _n) \big )_{n\in {\mathbb {N}}} \) in the space \([0,T] {\times }{\textbf{Q}}{\times }{\textbf{Q}}^*\) with \(t_n\rightarrow t\), \(q_n \rightharpoonup q \) in \({\textbf{Q}}\), \(\xi _n \rightharpoonup \xi \) in \({\textbf{Q}}^*\), \(\sup _n {\mathfrak {E}}(q_n) < \infty \), and \(\xi _n\in \partial _q {{\mathcal {E}}}(t, q_n)\), we have
Remark 4.6
For cases in which the energy space \({\textbf{U}}_{{\textrm{e}}}\) is compactly embedded into \({\textbf{U}}\), the sequences \((q_n)_n\) fulfilling the conditions of Hypothesis 4.5 converge strongly in \({\textbf{Q}}\) in view of the coercivity (4.7c). Therefore, in such cases Hypothesis 4.5 turns out to be a closedness condition on the graph of \(\partial _q {{\mathcal {E}}}\) with respect to the strong-weak topology of \({\textbf{Q}}{\times }{\textbf{Q}}^*\). When, instead, \({\textbf{U}}_{{\textrm{e}}}\) is only continuously embedded in \({\textbf{U}}\) (cf. Example 2.1 and (i) in (4.9)), the closedness requirement is in fact with respect to the weak-weak topology of \({\textbf{Q}}\). Then, the dominating term in the driving energy functionals needs to be quadratic, like in semilinear equations.
We also mention that, in contrast to what we did in [41] (cf. (2.E\(_5\)) therein), here in Hypothesis 4.5 we omit the requirement of energy convergence \( {\mathcal {E}}(t_n,q_n) \rightarrow {\mathcal {E}}(t,q) \) along the sequence \((t_n,q_n,\xi _n)_n\). In fact, that additional property was not strictly needed in the proof of the existence result [41, Thm. 2.2], to which we will resort later on to conclude the existence of solutions for our viscous system (4.11). Rather, in [41] the energy-convergence requirement was encompassed in the closedness assumption in order to pave the way for a weakening of the chain-rule condition, cf. the discussion in [41, Rmk. 4.6]. Such a weakening is outside the scope of this paper.
Our final condition on \({{\mathcal {E}}}\) is an abstract chain rule that has a twofold role: First, it is a crucial ingredient in the proof of Theorem 4.8, and secondly, it ensures the validity of the energy-dissipation balance (4.18). The latter will be the starting point in the derivation of our a priori estimates uniformly with respect to the viscosity parameter \(\varepsilon \). We refer to Proposition A.1 in Appendix A for a discussion of conditions on \({{\mathcal {E}}}\) yielding the validity of Hypothesis 4.7.
Hypothesis 4.7
(Chain rule) For every absolutely continuous curve \(q\in {\textrm{AC}}([0,T]; {\textbf{Q}})\) and all measurable selections \(\xi : (0,T) \rightarrow {\textbf{Q}}^*\) with \(\xi (t)\in \partial _q {{\mathcal {E}}}(t, {q(t)})\) for a.a. \(t\in (0,T)\),
we have the following two properties:

4.4 An Existence Result for the Viscous Problem
We are now in the position to state our existence result for the viscous system (4.11). It is based on the \((\Psi ,\Psi ^*)\)-formulation of the energy-dissipation balance (cf. (1.8) for the case \(q\mapsto {{\mathcal {E}}}(t,q)\) is smooth), which we now apply to (4.11) using the Fréchet subdifferential \(\partial _{\textsf{q}}{{\mathcal {E}}}(t,q)\) and the scaled dissipation potential \(\Psi _{\varepsilon ,\alpha }\) defined in (1.7). The Legendre–Fenchel conjugate is given by
It can be straightforwardly checked that the infimum in the definition of \({{\mathcal {W}}}^*_{\textsf{z}}\) is attained.
Theorem 4.8
(Existence of viscous solutions) Assume Hypotheses 4.2, 4.3, 4.5, and 4.7. Then, for every \(\varepsilon \in (0,1]\) and \(q_0 = (u_0,z_0)\in {\mathscr {D}}\) there exist a curve \(q=(u,z) \in {\textrm{AC}}([0,T];{\textbf{Q}})\) and a function \(\xi =(\mu ,\zeta ) \in {\textrm{L}}^1(0,T;{\textbf{U}}^* {\times }{\textbf{Z}}^*)\) fulfilling the initial condition \(q(0) = q_0\) and solving the generalized gradient system (4.11) in the sense that for a.a. \(r\in (0,T)\)
Moreover, for \(0\le s < t \le T\), these functions satisfy the energy-dissipation balance
where \({{\mathcal {V}}}_{\textsf{x}}^{\lambda }\) is defined in (1.5a).
Proof
Since we are in the simple setting of [41, Sec. 2], where the dissipation potential \(\Psi _{\varepsilon ,\alpha }\) does not depend on the state q, we can appeal to [41, Thm. 2.2]. Thus, it suffices to check the assumptions (2.\(\Psi _1\))–(2.\(\Psi _3\)), (E\(_0\)), and (2.E\(_1\))–(2.E\(_4\)) therein. Our Hypothesis 4.2 clearly implies (2.\(\Psi _1\)) and (2.\(\Psi _2\)). Hypothesis 4.3 implies the assumptions (E\(_0\)) via (4.7a) and (4.7b), and assumption (2.E\(_1\)) follows via (4.7c) and Hypothesis 4.2. Assumption (2.E\(_2\)) follows from Hypothesis 4.5 via [41, Prop. 4.2]. Assumption (2.E\(_3\)) equals (4.7d) in Hypothesis 4.3. Finally, leaving out the energy-convergence requirement assumption (2.E\(_5\)) follows from Hypothesis 4.5.
Thus, all assumptions are satisfied except for (2.\(\Psi _3\)) and (2.E\(_4\)). Concerning (2.\(\Psi _3\)), we observe that this technical condition was used for the proof of [41, Thm. 2.2] only in one place, namely in the proof of Lemma 6.1 there. In [5, Thm. 3.2.3] or in [32] it is shown that Lemma 6.1, which is also called “De Giorgi’s lemma”, is also valid if the condition [41, Eqn. (2.\(\Psi _3\))] is replaced by the condition that the underlying space Banach space \({\textbf{Q}}\) is reflexive, but this is true by our Hypothesis 4.1. As for the chain rule [41, (2.E\(_4\))], a close perusal of the proof of [41] shows that our Hypothesis 4.7 can replace it, allowing us to conclude the existence statement. \(\square \)
Remark 4.9
(Energy-dissipation inequality) The analysis from [41] in fact reveals that, under the chain rule in Hypothesis 4.7, a curve \(q\in {\textrm{AC}}([0,T];{\textbf{Q}})\) fulfills (4.18a) if and only if the pair \((q,\xi )\) satisfies the energy-dissipation balance (4.18b) which, again by the chain rule, is in turn equivalent to the upper energy-dissipation estimate \(\le \). This characterization of the viscous system will prove handy for the analysis of the delamination system from Sect. 8.
4.5 Properties of the Generalized Slopes
For the further analysis it is convenient to introduce the generalized slope functionals \({\mathscr {S}}_{\textsf{x}}^*: [0,T]{\times }{\mathscr {D}}\rightarrow [0,\infty ]\), \({\textsf{x}} \in \{{\textsf{u}}, {\textsf{z}}\}\) via
where the infimum over the empty set is always \(+\infty \). These functionals play the same key role as (the square of) the metric slope for metric gradient systems, hence from now on we shall refer to \({\mathscr {S}}_{\textsf{u}}^*\) and \({\mathscr {S}}_{\textsf{z}}^*\) as generalized slopes. Clearly, energy balance (4.18b) entails the validity of the following energy-dissipation estimate featuring the slopes \({\mathscr {S}}_{\textsf{u}}^*\) and \({\mathscr {S}}_{\textsf{z}}^*\):
Note that (4.20) is weaker than (4.18b), but it has the advantage that the selections \(\xi =(\mu ,\zeta )\) in (4.18a) are no longer needed. Moreover, (4.20) will be still strong enough to handle the limit passage \(\varepsilon \rightarrow 0^+\). For this, we will assume that the infima in (4.19) are attained. We set
In fact, it can be checked (e.g. by resorting to [41, Prop. 4.2]), that \({\textrm{dom}}(\partial _q {{\mathcal {E}}}(t,\cdot ))\) is dense in \({\mathscr {D}}\).
Hypothesis 4.10
(Attainment and lower semicontinuity) For all \((t,q) \in {\textrm{dom}} (\partial _q {{\mathcal {E}}})\) the infima in (4.19) are attained, namely
where \({\mathcal {W}}_{\textsf{z}}^*\) is defined in (4.17). Furthermore, for all sequences \((t_n,q_n)_n\subset [0,T] {\times }{\textbf{Q}}\) with \(t_n\rightarrow t\), \(q_n \rightharpoonup q\) in \({\textbf{Q}}\), and \(\sup _{n\in {\mathbb {N}}} {\mathfrak {E}}(q_n) \le C<\infty \) there holds
We are going to show in Lemma 4.11 below that a sufficient condition for Hypothesis 4.10 is that (4.12) improves to an equality, namely
Observe that (4.23) does hold if, for instance, \({{\mathcal {E}}}\) is of the form
Lemma 4.11
Assume Hypotheses 4.2, 4.3, 4.5, as well as (4.23). Then,
for all \((t,q) \in [0,T]{\times }{\textrm{dom}}(\partial _q {{\mathcal {E}}}) \), and properties (4.21) and (4.22) hold.
Proof
Obviously, for \((t,q)\in {\textrm{dom}}(\partial _q {{\mathcal {E}}})\) we have (4.24) as a consequence of (4.23). We will just check the attainment (4.21) and the lower semicontinuity (4.22) for \({\mathscr {S}}_{\textsf{z}}^*\), as the properties for \({\mathscr {S}}_{\textsf{u}}^*\) follow by the same arguments.
Suppose that \((t_n,q_n) \rightharpoonup (t,q)\) and \(\liminf _{n\rightarrow \infty } {\mathscr {S}}_{\textsf{z}}^*(t_n,q_n) <\infty \). Using (4.24), up to a subsequence, there exist \((\zeta _n)_n \subset {\textbf{Z}}^*\) with \(\zeta _n \in \partial _{\textsf{z}}{{\mathcal {E}}}(t_n,q_n) \) and \((\sigma _n)_n \subset \partial {{\mathcal {R}}}(0) \subset {\textbf{Z}}^*\) for all n with
It follows from (4.2) that the sequence \((\sigma _n{+}\zeta _n)_n\) is bounded in \({\textbf{Z}}^*\). Since, in view of (4.6), \((\sigma _n)_n\) is bounded in \({\textbf{Z}}^*\), \((\zeta _n)_n\) turns out to be bounded in \({\textbf{Z}}^*\), too. Then, up to a subsequence we have \(\sigma _n\rightharpoonup \sigma \) in \({\textbf{Z}}^*\) and \(\zeta _n\rightharpoonup \zeta \) in \({\textbf{Z}}^*\). Since \(\partial {{\mathcal {R}}}(0)\) is sequentially weakly closed in \({\textbf{Z}}^*\), we find \(\sigma \in \partial {{\mathcal {R}}}(0)\). By Hypothesis 4.5 we also have \(\zeta \in \partial _{\textsf{z}}{{\mathcal {E}}}(t,q) \), hence
which is the desired lsc (4.22) for \({\mathscr {S}}_{\textsf{z}}^*\).
With similar arguments we deduce the attainment (4.21). \(\square \)
In the above proof we have used in an essential way that \(\partial {{\mathcal {R}}}(0)\) is bounded in \({\textbf{Z}}^*\) by our assumption (4.3b). Without this property, the argument still goes through provided that, given a sequence \((q_n)_n\subset {\textbf{Q}}\) as in Hypothesis 4.10, all sequences \((\zeta _n)_n\) with \(\zeta _n\in {\mathfrak {A}}_{\textsf{z}}^{*}(t_n,q_n)\) for all \(n\in {\mathbb {N}}\) happen to be bounded in \({\textbf{U}}^* {\times }{\textbf{Z}}^*\), which can be, of course, an additional property of the subdifferential \(\partial _{\textsf{z}} {{\mathcal {E}}}\).
Throughout the rest of this paper, we will always tacitly assume the validity of Hypotheses 4.1, 4.2, 4.3, 4.5, 4.7, and 4.10 and omit any explicit mentioning of them in most of the upcoming results (with the exception of our main existence theorems).
4.6 A Priori Estimates for the Viscous Solutions
Let \((q_\varepsilon )_\varepsilon \) be a family of solutions to the viscously regularized systems (1.4) in the stricter sense of (4.18), which includes the energy-dissipation balance (4.18b). By Theorem 4.8 the existence of solutions \(q_\varepsilon =(u_\varepsilon ,z_\varepsilon )\) is guaranteed, and in this subsection we discuss some a priori estimates on \((u_\varepsilon ,z_\varepsilon )_\varepsilon \) that are uniform with respect to the parameter \(\varepsilon \) and that form the core of our vanishing-viscosity analysis.
The starting point is the energy-dissipation estimate (4.20) that follows directly from (4.18b). Recalling the constant \(C_\#\) from (4.7d) in Hypothesis 4.3 and \(c_{{\mathcal {R}}}\) in Hypothesis 4.2, we see that the following basic a priori estimates are valid under the sole assumptions of Hypotheses 4.2 and 4.3.
Lemma 4.12
(Basic a priori estimates) For all \(\varepsilon >0\) and all solutions \(q_\varepsilon =(u_\varepsilon ,z_\varepsilon ):[0,T] \rightarrow {\textbf{Q}}={\textbf{U}}{\times }{\textbf{Z}}\) of (4.18) with \({{\mathcal {E}}}(0,q_\varepsilon (0))< \infty \) we have the a priori estimates
whence, in particular,
Proof
The proof follows as in the purely rate-independent case treated in [29, Cor 3.3]. We start from (4.18b) and drop the nonnegative dissipation to obtain
where we used (4.7d). Thus, Grönwall’s estimate gives (4.25b), and from this we find that
and (4.25a) is established as well, as \({{\mathcal {E}}}(T,q_\varepsilon (T))\ge C_0>0\) by (4.7b).
Since \({{\mathcal {V}}}_{\textsf{x}}\) and \({\mathscr {S}}_{\textsf{x}}^*\) are nonnegative, assumption (4.3b) leads to the first estimate in (4.26). The last assertion follows from (4.25b) and applying (4.7d) once again. \(\square \)
Clearly, (4.26) provides a uniform bound on the total variation of the solution component \(z_\varepsilon \) in the space \({\textbf{Z}}_{{\textrm{ri}}}\). A similar bound cannot be expected for the components \(u_\varepsilon \), unless we add further assumptions. To see the problem consider \({\textbf{U}}= {\mathbb {R}}^2\) and the ordinary differential equation
with \(\lambda \ge 0\). Note that \(\varphi \) is uniformly coercive for all \(\lambda \ge 0\). However, the equation is linear for \(|u|\le 1\) and has an exact periodic solution of the form
as long as \(|U(t)|\le 1\), i.e. \(a^2\le \lambda ^2{+}\omega ^2\varepsilon ^{2\alpha }\). In this case, the derivatives satisfy the following \({\textrm{L}}^1\)-estimates:
For \(\lambda >0\) we thus obtain a bound on \(\Vert u'_\varepsilon \Vert _{{\textrm{L}}^1(0,T)}\) from a bound on \(\Vert z'_\varepsilon \Vert _{{\textrm{L}}^1(0,T)}\) as in (4.26). However, in the case \(\lambda =0\) the value \(\Vert u'_\varepsilon \Vert _{{\textrm{L}}^1(0,T)}\) may blow up while \(\Vert z'_\varepsilon \Vert _{{\textrm{L}}^1(0,T)}\) remains bounded (or even tends to 0) and \(a^2 \le \omega ^2\varepsilon ^{2\alpha }\), e.g. choosing \(\omega =\varepsilon ^{-\alpha /2}\) and \(a=\varepsilon ^{2\alpha /\alpha }\).
In the main part of this subsection, we provide sufficient conditions for the validity of a uniform bound on \(\Vert u'_\varepsilon \Vert _{{\textrm{L}}^1(0,T;{\textbf{U}})} \). In the spirit of the above ODE example we assume that \(u \mapsto {\mathcal {E}}(t,u,z)\) is uniformly convex (i.e. \(\lambda >0\)) and that \(z \mapsto {\textrm{D}}_u{\mathcal {E}}(t,u,z)\) is Lipschitz. Moreover, we need to assume that \({{\mathcal {V}}}_{\textsf{u}}\) is quadratic. More precisely, we have to confine the discussion to a special setup given by conditions (4.27) and (4.28).
-
(1)
The dissipation potential \({{\mathcal {V}}}_{\textsf{u}} \) is quadratic:
$$\begin{aligned} {\textbf{U}}\text { is a Hilbert space and }{{\mathcal {V}}}_{\textsf{u}}(v): = \frac{1}{2}\Vert v \Vert _{{\textbf{U}}}^2= \frac{1}{2}\langle {\mathbb {V}}_{\textsf{u}}v,v\rangle . \end{aligned}$$(4.27)there \({\mathbb {V}}_{\textsf{u}}:{\textbf{U}}\rightarrow {\textbf{U}}^*\) is Riesz’ norm isomorphism;
-
(2)
The energy functional \({{\mathcal {E}}}\) has domain \({\mathscr {D}}= {\mathscr {D}}_{\textsf{u}} {\times }{\mathscr {D}}_{\textsf{z}}\) and admits the decomposition
$$\begin{aligned}&{\mathcal {E}}(t,u, z) = {{\mathcal {E}}}_1(u) + {{\mathcal {E}}}_2(t,u,z) \quad \text {with} \end{aligned}$$(4.28a)$$\begin{aligned}&\exists \,\Lambda >0: {{\mathcal {E}}}_1 \text { is }\Lambda \text {-convex}, \end{aligned}$$(4.28b)$$\begin{aligned}&\forall \, (t,z ) \in [0,T]{\times }{\mathscr {D}}_{\textsf{z}}: u\mapsto {{\mathcal {E}}}_2(t,u,z) \text { is Fr}\acute{\textrm{e}}\text {chet differentiable on } {\mathscr {D}}_{\textsf{u}}, \end{aligned}$$(4.28c)$$\begin{aligned}&\exists \, C_{\textsf{u}}\in (0,\Lambda ) \ \forall \, E>0 \ \exists \, C_E>0 \ \forall \, t_1, t_2 \in [0,T] \ \forall \, (u_1,z_1), (u_2,z_2) \in {\mathcal {S}}_{E} : \nonumber \\&\quad \Vert {\textrm{D}}_{\textsf{u}}{{\mathcal {E}}}_2(t_1,u_1,z_1){-} {\textrm{D}}_{\textsf{u}}{{\mathcal {E}}}_2(t_2,u_2,z_2)\Vert _{{\textbf{U}}^*} \nonumber \\&\quad \le C_E \left( |t_1{-}t_2| + \Vert z_1{-}z_2\Vert _{{\textbf{Z}}_{{\textrm{ri}}}} \right) + C_{\textsf{u}}\Vert u_1{-}u_2\Vert _{\textbf{U}}, \end{aligned}$$(4.28d)where \({\mathcal {S}}_{E}\) denotes the sublevel of \({\mathfrak {E}}\), cf. (4.8).
Hence, the possibly nonsmooth, but uniformly convex functional \({{\mathcal {E}}}_1\) is perturbed by the smooth, but possibly nonconvex, functional \(u\mapsto {{\mathcal {E}}}_2 (t,u,z)\). However, by \(C_{\textsf{u}}<\Lambda \) the mapping \(u\mapsto {{\mathcal {E}}}(t,u,z)\) is still uniformly convex. We emphasize that in this context, the norm of the space \({\textbf{Z}}_{{\textrm{ri}}}\) features in (4.28d) and controls the coupling of z into the equation for u.
Unfortunately condition (4.28) is rather restrictive, because in concrete examples the driving energy functional features a coupling between the variables u and z that is more complex. Nevertheless the desired a priori estimate derived in Proposition 4.13 may still be valid. Indeed, for our delamination model examined in Sect. 8 we establish the corresponding estimate via an ad hoc approach for the specific system.
The proof of the next results follow the technique for the a priori estimate developed in [30, Prop. 4.17]. We emphasize that the two additional assumptions (4.27) and (4.28) yield that the solution \(u_\varepsilon \) for \({\mathbb {V}}_{\textsf{u}}u' + \partial {{\mathcal {E}}}_1(u) + {\textrm{D}}{{\mathcal {E}}}_1(t,u,z_\varepsilon (t)) \ni 0\) is unique as long as \(z_\varepsilon \) is kept fixed, since it is a classical Hilbert-space gradient flow for a time-dependent, convex functional.
Proposition 4.13
(\({\textrm{L}}^1\) bound on \(u'_\varepsilon \)) In addition to Hypotheses 4.2 and 4.3 assume (4.27) and (4.28) and consider initial conditions \((q_\varepsilon ^0)_\varepsilon \) such that
where \(\partial ^0_{\textsf{u}}{{\mathcal {E}}}(0,q_\varepsilon ^0)\subset {\textbf{U}}^*\) denotes the unique element of minimal norm in \(\partial _{\textsf{u}}{{\mathcal {E}}}(0,q_\varepsilon ^0)\subset {\textbf{U}}^*\). Then, there exists a constant \(C>0\) such that for all \(\varepsilon \in (0,1)\) all solutions \(q_\varepsilon = (u_\varepsilon , z_\varepsilon )\) of system (4.18) with \(q_\varepsilon (0)=q_\varepsilon ^0\) satisfy

Proof
By Lemma 4.12 all curves \(q_\varepsilon :[0,T] \rightarrow {\textbf{Q}}\) lie in \({{\mathcal {S}}}_E=\left\{ \, q\in {\textbf{Q}}\, \big | \, {\mathfrak {E}}(q)\le E \,\right\} \) for \(E=\mathrm e^{2C_\# T} C_{\textrm{init}}\). Throughout the rest of this proof we drop the subscripts \(\varepsilon \) at \(q_\varepsilon =(u_\varepsilon ,z_\varepsilon )\), but keep all constants explicitly to emphasize that they do not depend on \(\varepsilon \).
We write the equation for u in the form \(0=\varepsilon ^\alpha {\mathbb {V}}_{\textsf{u}}u'(t)+ \mu (t) \) with \(\mu (t)\in \partial _{\textsf{u}}{{\mathcal {E}}}(t,u(t),z(t))\). For small \(h>0\) and \(t\in [0,T{-}h]\) we find
where we have used that the selection \(\mu (t) \in \partial _{\textsf{u}}{{\mathcal {E}}}(t,u(t),z(t))\) is given by \(\mu (t) = \mu _1(t)+\mu _2(t)\), with \(\mu _1(t) \in \partial _{\textsf{u}}{{\mathcal {E}}}_1(u(t))\) and \(\mu _2(t) = {\textrm{D}}_{\textsf{u}}{{\mathcal {E}}}_2(t,u(t),z(t))\), and we have also used the place-holder \({\widetilde{\mu }}_{2,h}(t) = {\textrm{D}}_{\textsf{u}}{{\mathcal {E}}}_2(t,u(t{+} h),z(t))\). Now, by the \(\Lambda \)-convexity of \({{\mathcal {E}}}_1\) we have that

In turn, (4.28d) yields
All in all, setting \(\kappa = \Lambda - C_{\textsf{u}}\) we conclude that
where \(\varrho _h(t):= \Vert u(t{+}h){-}u(t)\Vert _{\textbf{U}}\). Choosing \(\delta >0\) and setting \(\nu _h(t):=\varrho _h(t)^2{+}\delta \) yields
Integrating this inequality in time we arrive at
Taking the limit \(\delta \rightarrow 0^+\), dividing by \(h>0\), and using \(\Vert z(t{+}h){-}z(t)\Vert _{{\textbf{Z}}_{{\textrm{ri}}}}\le \int _t^{t+h} \Vert z'(s)\Vert _{{\textbf{Z}}_{{\textrm{ri}}}} \,\,\!{\textrm{d}}s\) gives
Since the equation for u is a Hilbert-space gradient flow we can apply [7, Thm. 3.1], which shows that \(\frac{1}{h}(u(h){-}u(0)) \rightarrow \partial ^0_{\textsf{u}}{{\mathcal {E}}}(0,u(0),z(0))\) for \(h\rightarrow 0^+\). Thus, taking the limit \(h\rightarrow 0^+\) we find
which is the desired result, upon recalling \(\kappa = \Lambda - C_{\textsf{u}}\). \(\square \)
The above result is valid for all solutions of the viscous system (4.18), but it relies on the rather strong assumptions (4.27) and (4.28). While the uniform convexity of \(u \mapsto {\mathcal {E}}(t,u, z)\) in (4.28) seems to be fundamental (see however Remark 4.14 below), it is expected that the rather strong assumption that \({{\mathcal {V}}}_{\textsf{u}} \) is the square of a Hilbert space norm, cf. (4.27), can be relaxed, but then the solution \(u_\varepsilon \) may no longer be uniquely determined for fixed \(z_\varepsilon \). In that case it may be helpful to restrict the analysis to specific solution classes satisfying better a priori estimates, e.g. to minimizing movements obtained via time-incremental minimization problems as in [42, Thm. 3.23] or to solutions obtained as limit of Galerkin approximations as in [36, Def. 4.3 & Thm. 4.13]. We also refer to our delamination model in Sect. 8 for a derivation of the additional a priori estimate (4.29) in a more difficult case.
Remark 4.14
Condition (4.28b) has played a key role in proving an a priori estimate for \(\int _0^T \Vert u_\varepsilon '(t)\Vert _{\textbf{U}}\,\,\!{\textrm{d}}t \), cf. (4.31) where the modulus of convexity \(\Lambda \) explicitly appears. Nonetheless, it could be expected that, relaxing the uniform convexity of \(u \mapsto {\mathcal {E}}(t,u, z)\) to a strict convexity condition might still be useful. Although it could no longer be instrumental in proving a \(\text {BV}\) bound for the curves \(u_\varepsilon \), strict convexity would indeed ensure that the inclusion \( \partial _{\textsf{u}}{{\mathcal {E}}}(t,u,z) \ni 0 \) has a unique solution \(u=U(t,z)\). This would prevent oscillations for the sequence \((u_\varepsilon )_\varepsilon \) upon taking the vanishing-viscosity limit.
We refrain from working out this generalization as, then, we would have to be much more careful in obtaining the chain rule necessary for our exact energy-dissipation balance.
5 Parametrized Balanced-Viscosity Solutions
In this section we will give the definition of Balanced-Viscosity solution to the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) in a parametrized version. For this, we study instead of the viscous solutions \(q_\varepsilon :[0,T] \rightarrow {\textbf{Q}}\) suitable reparametrizations \(({\textsf{t}}_\varepsilon ,{\textsf{q}}_\varepsilon ):[0,{{{\textsf {S}}}}_\varepsilon ] \rightarrow [0,T]{\times }{\textbf{Q}}\), i.e., \({\textsf{q}}_\varepsilon (s)=q_\varepsilon ({\textsf{t}}_\varepsilon (s))\), see Sect. 5.1. While quite general reparametrizations are possible, we will perform the vanishing-viscosity limit \(\varepsilon \rightarrow 0^+\) for the one given in terms of the energy-dissipation arclength \(s={\textsf{s}}_\varepsilon (t)\) defined in terms of the rescaled joint M-function \({\mathfrak {M}}_{\varepsilon }^{\alpha }\) arising from the rescaled joint B-function \( {\mathfrak {B}}^\alpha _\varepsilon \), see (5.2). The \(\Gamma \)-limit \({\mathfrak {M}}_{0}^{\alpha }\) of \({\mathfrak {M}}_{\varepsilon }^{\alpha }\), which is called the limiting rescaled joint M-function, will then be used, to introduce the concept of admissible parametrized curves, see Definition 5.6 in Sect. 5.2. This is the basis of our notion of for parametrized Balanced-Viscosity (\(\text {pBV}\)) solutions, defined in Sect. 5.3. Theorem 5.12 states our main existence result for \(\text {pBV}\) solutions, which is based on the convergence in the vanishing-viscosity limit \(\varepsilon \rightarrow 0^+\). However, we emphasize that the notion of ‘\(\text {pBV}\) solutions’ is independent of the limiting procedure. Finally, in Sect. 5.5 we provide a characterization of (enhanced) \(\text {pBV}\) solutions showing that they are indeed solutions of the time-rescaled generalized gradient system (1.13).
5.1 Reparametrization and Rescaled Joint M-Functions
This subsection revolves around the concept and the properties of the limiting rescaled joint M-function \({\mathfrak {M}}_{0}^{\alpha }\) that will be introduced in the Definition 5.1. First, we will prove that \({\mathfrak {M}}_{0}^{\alpha }\) is the \(\Gamma \)-limit of the family of M-functions \(({\mathfrak {M}}_{\varepsilon }^{\alpha })_\varepsilon \) that appear naturally in the reparametrized version of the energy-dissipation estimate (4.20) and that are given by a composition of the rescaled joint B-function \({\mathfrak {B}}_\varepsilon ^\alpha \) and the slopes \({\mathscr {S}}_{\textsf{x}}^*\). Namely, the M-functions are defined by
where \( {\mathfrak {B}}_\varepsilon ^\alpha \) is the rescaled joint B-function from (3.16) associated with the dissipation potentials \(\psi _{\textsf{u}}= {{\mathcal {V}}}_{\textsf{u}}\) and \(\psi _{{\textsf{z}}} ={{\mathcal {R}}}{+} {{\mathcal {V}}}_{\textsf{z}}\).
The basis for the construction of parametrized BV solutions is the reparametrization of the the viscous solutions \(q_\varepsilon :[0,T]\rightarrow {\textbf{Q}}\) in the form \({\textsf{q}}_\varepsilon (s)=q_\varepsilon ({\textsf{t}}_\varepsilon (s))\) such that the behavior of the function \(({\textsf{t}}_\varepsilon ,{\textsf{q}}_\varepsilon ):[0,{{{\textsf{S}}}}_\varepsilon ]\rightarrow [0,T]{\times }{\textbf{Q}}\) is advantageous. In particular, the formation of jumps in \(q_\varepsilon \) with \(\Vert q'_\varepsilon (t)\Vert \approx 1/\varepsilon \) can be modeled by a plateau-like behavior of \({\textsf{t}}_\varepsilon \) with \({\textsf{t}}'_\varepsilon (s)\approx \varepsilon \) and a soft transition of \({\textsf{q}}_\varepsilon \) with \(\Vert {\textsf{q}}'_\varepsilon (s)\Vert \approx 1\). The first usage of such reparametrizations for the vanishing-viscosity limit goes back to [14], but here we stay close to [42, Sec. 4.1] in using an ‘energy-based time reparametrization’. Hence, for a family \((q_\varepsilon )_\varepsilon =(u_\varepsilon , z_\varepsilon )_\varepsilon \) of solutions to (1.4) for which the estimates from Lemma 4.12 hold, as well as the additional a priori estimate (4.29) on \(\int _0^T\Vert u'_\varepsilon \Vert _{\textbf{U}}\,\,\!{\textrm{d}}t\), we reparametrize the functions \(q_\varepsilon \) using the energy-dissipation arclength \({\textsf{s}}_\varepsilon : [0,T]\rightarrow [0,{{{\textsf {S}}}}_\varepsilon ]\) with \({{{\textsf {S}}}}_\varepsilon := {\textsf{s}}_\varepsilon (T)\) (cf. [42, (4.3)]) defined by
such that estimates (4.25) and (4.29) yield that \(\sup _{\varepsilon >0} {{{\textsf {S}}}}_\varepsilon \le C\). Below we consider the reparametrized curves \(({\textsf{t}}_\varepsilon , {\textsf{q}}_\varepsilon ): [0,{{{\textsf {S}}}}_\varepsilon ] \rightarrow [0,T]{\times }{\textbf{Q}}\) defined by \({\textsf{t}}_\varepsilon : = {\textsf{s}}_\varepsilon ^{-1}\), \({\textsf{q}}_\varepsilon : = q_\varepsilon \circ {\textsf{t}}_\varepsilon \) and show in Sect. 5.3 that they have an absolutely continuous limit \(({\textsf{t}},{\textsf{q}})\), up to choosing a subsequence.
We first remark that the quantities involved in the definition of \({\textsf{s}}_\varepsilon \) rewrite as
With this, the energy-dissipation estimate (4.20) can be rewritten in terms of the parametrized curves \(({\textsf{t}}_\varepsilon , {\textsf{q}}_\varepsilon ) \) in the form (for all \(0\le s_1< s_2 \le {{{\textsf {S}}}}_\varepsilon \))
Moreover, the definition of \({\textsf{s}}_\varepsilon \) in (5.2) is equivalent to the normalization condition
Of course, the reparametrized solutions \({\textsf{q}}_\varepsilon \) inherit the energy estimate (4.26), namely,
The a priori estimates (5.5) and (5.6) for the reparametrized curves \(({\textsf{t}}_\varepsilon ,{\textsf{q}}_\varepsilon )_\varepsilon \) will be strong enough to ensure their convergence along a subsequence, as \(\varepsilon \rightarrow 0^+\), to a curve \(({\textsf{t}},{\textsf{q}}): [0,{{{\textsf {S}}}}]\rightarrow [0,T]{\times }{\textbf{Q}}\), with \({{{\textsf {S}}}}= \lim _{\varepsilon \rightarrow 0^+}{{{\textsf {S}}}}_\varepsilon \). The basic properties of \(({\textsf{t}},{\textsf{q}})\) are fixed in the concept of admissible parametrized curve, see Definition 5.6.
For studying the limit \(\varepsilon \rightarrow 0^+\), we need to bring into play the limiting rescaled joint M-function \( {\mathfrak {M}}_{0}^{\alpha }\).
Definition 5.1
We define \( {\mathfrak {M}}_{0}^{\alpha }: [0,T]{\times }{\mathscr {D}}{\times }[0,\infty ) {\times }{\textbf{Q}}\rightarrow [0,\infty ] \) via
where \({\mathfrak {B}}_0^\alpha \) is defined in Proposition 3.7 and \(\overline{{\textrm{dom}}(\partial _{\textsf{q}}{{\mathcal {E}}})}^{{\textrm{w,S}}} \) is the weak closure of \( {\textrm{dom}}(\partial _{\textsf{q}}{{\mathcal {E}}})\) confined to energy sublevels:
It follows from Proposition 3.7 that
Relying on Proposition 3.7 and Hypothesis 4.10, we are ready to prove the following \(\Gamma \)-convergence result, which straightforwardly gives that \( {\mathfrak {M}}_{0}^{\alpha }\) is (sequentially) lower semicontinuous with respect to the weak topology of \({\mathbb {R}}{\times }{\textbf{Q}}{\times }{\mathbb {R}}{\times }{\textbf{Q}}\) along sequences with bounded energy.
Proposition 5.2
(Weak \(\Gamma \)-convergence of M-functions) The limiting M-function \({\mathfrak {M}}_{0}^{\alpha }: [0,T]{\times }{\mathscr {D}}{\times }[0,\infty ) {\times }{\textbf{Q}}\rightarrow [0,\infty ]\) is the \(\Gamma \)-limit of the M-functions \(({\mathfrak {M}}_{\varepsilon }^{\alpha })_\varepsilon \), with respect to the weak topology, along sequences with bounded energy, namely the following assertions hold:
-
(a)
\(\Gamma \)-\(\liminf \) estimate:
$$\begin{aligned}&\Big ((t_\varepsilon ,q_\varepsilon ,{t_\varepsilon '}, q_\varepsilon ')\rightharpoonup (t,q,t', q') \text { in } {\mathbb {R}}{\times }{\textbf{Q}}{\times }{\mathbb {R}}{\times }{\textbf{Q}}\text { as } \varepsilon \rightarrow 0^+ \ \text { with } \sup _{\varepsilon >0} {\mathfrak {E}}(q_\varepsilon )< \infty \Big )\nonumber \\&\quad \Longrightarrow \quad {\mathfrak {M}}_{0}^{\alpha }(t,q, t',q') \le \liminf _{\varepsilon \rightarrow 0^+} {\mathfrak {M}}_{\varepsilon }^{\alpha }(t_\varepsilon ,q_\varepsilon , t_\varepsilon ',q_\varepsilon '); \end{aligned}$$(5.10a) -
(b)
\(\Gamma \)-\(\limsup \) estimate:
$$\begin{aligned}&\forall \, (t,q,t',q') \in [0,T]{\times }{\mathscr {D}}{\times }[0,\infty ) {\times }{\textbf{Q}}\ \exists \, (t_\varepsilon ,q_\varepsilon ,t_\varepsilon ',q_\varepsilon ')_\varepsilon \text { such that }\nonumber \\&\quad \;\ \text {(i)} \quad (t_\varepsilon ,q_\varepsilon , t_\varepsilon ', q_\varepsilon ') \rightharpoonup (t,q,t',q') \text { in } {\mathbb {R}}{\times }{\textbf{Q}}{\times }{\mathbb {R}}{\times }{\textbf{Q}}\text { as } \varepsilon \rightarrow 0^+,\nonumber \\&\quad \ \text {(ii)} \quad \sup \nolimits _{\varepsilon >0} {\mathfrak {E}}(q_\varepsilon ) < \infty , \text { and }\nonumber \\&\quad \text {(iii)} \quad {\mathfrak {M}}_{0}^{\alpha }(t,q, t',q') \ge \limsup \nolimits _{\varepsilon \rightarrow 0^+} {\mathfrak {M}}_{\varepsilon }^{\alpha }(t_\varepsilon ,q_\varepsilon , t_\varepsilon ',q_\varepsilon '). \end{aligned}$$(5.10b)
Proof
Concerning (a), let \( (t_\varepsilon ,q_\varepsilon ,{t_\varepsilon '}, q_\varepsilon ')_\varepsilon \) be a sequence as in (5.10a). Of course we can suppose that \(\liminf _{\varepsilon \rightarrow 0^+} {\mathfrak {M}}_{\varepsilon }^{\alpha }(t_\varepsilon ,q_\varepsilon , t_\varepsilon ',q_\varepsilon ')<\infty \), and thus that \(\sup _\varepsilon {\mathfrak {M}}_{\varepsilon }^{\alpha }(t_\varepsilon ,q_\varepsilon , t_\varepsilon ',q_\varepsilon ')<\infty \). Then, there exists \({{\bar{\varepsilon }}}>0\) such that for all \(\varepsilon \in (0,{{\bar{\varepsilon }}})\) there holds \(t_\varepsilon ' > 0\), the Fréchet subdifferential \(\partial _{\textsf{q}}{{\mathcal {E}}}(t_\varepsilon ,q_\varepsilon ) \) is non-empty, and \({\mathfrak {M}}_{\varepsilon }^{\alpha }(t_\varepsilon ,q_\varepsilon , t_\varepsilon ',q_\varepsilon ') = {\mathfrak {B}}_\varepsilon ^\alpha (t_\varepsilon ', u_\varepsilon ',z_\varepsilon ', {\mathscr {S}}_{\textsf{u}}^*(t_\varepsilon ,q_\varepsilon ), {\mathscr {S}}_{\textsf{z}}^*(t_\varepsilon ,q_\varepsilon )) \). In order to apply Proposition 3.7 we now need to discuss the boundedness of the slopes \( ({\mathscr {S}}_{\textsf{u}}^*(t_\varepsilon ,q_\varepsilon ))_\varepsilon \), \(({\mathscr {S}}_{\textsf{z}}^*(t_\varepsilon ,q_\varepsilon ))_\varepsilon \). Indeed, If \(t'>0\), then \(t_\varepsilon '\ge c>0\) for all \(\varepsilon \in (0,{{\bar{\varepsilon }}})\) (up to choosing a smaller \({{\bar{\varepsilon }}}\)), so that, by the definition (3.14) of \({\mathfrak {B}}_\varepsilon ^\alpha \) we infer that \( {\mathscr {S}}_{\textsf{u}}^*(t_\varepsilon ,q_\varepsilon ) \le C \varepsilon ^\alpha \) and \( {\mathscr {S}}_{\textsf{z}}^*(t_\varepsilon ,q_\varepsilon ) \le C \varepsilon \) for all \(\varepsilon \in (0,{{\bar{\varepsilon }}})\). In the case \(t'=0\), suppose e.g. that \(\liminf _{\varepsilon \rightarrow 0}{\mathscr {S}}_{\textsf{u}}^*(t_\varepsilon ,q_\varepsilon )=\infty \) while \(\liminf _{\varepsilon \rightarrow 0}{\mathscr {S}}_{\textsf{z}}^*(t_\varepsilon ,q_\varepsilon )<\infty \). Then, from the coercivity estimate (3.17b) we deduce (up to extracting a not relabeled subsequence) that \(u_\varepsilon '\rightarrow 0\). Thus,
with the latter estimate due to Proposition 3.7, Hypothesis 4.10, and the monotonicity of \({\mathfrak {B}}^\alpha _0(\tau ,q',\sigma _{\textsf{u}},\sigma _{\textsf{z}})\) in \(\sigma _{\textsf{u}}\) and \(\sigma _{\textsf{z}}\). We may argue similarly in the case \(\liminf _{\varepsilon \rightarrow 0}{\mathscr {S}}_{\textsf{u}}^*(t_\varepsilon ,q_\varepsilon )< \infty \) and \(\liminf _{\varepsilon \rightarrow 0}{\mathscr {S}}_{\textsf{z}}^*(t_\varepsilon ,q_\varepsilon )=\infty \) and when both limits are finite.
The \(\Gamma \)-\(\limsup \) estimate (b) is trivial for all \( (t,q,t',q') \in [0,T]{\times }{\mathscr {D}}{\times }[0,\infty ) {\times }{\textbf{Q}}\) with \({\mathfrak {M}}_{0}^{\alpha }(t,q, t',q')=\infty \). If \({\mathfrak {M}}_{0}^{\alpha }(t,q, t',q') = {\mathfrak {B}}_0^\alpha (t',u',z',{\mathscr {S}}_{\textsf{u}}^*(t,q), {\mathscr {S}}_{\textsf{z}}^*(t,q))<\infty \), then the \(\limsup \) estimate immediately follows via the constant recovery sequence \((t_\varepsilon , q_\varepsilon , t_\varepsilon ', q_\varepsilon ') \equiv (t,q,t',q')\) with the same arguments as in the proof of Proposition 3.7. Let us now suppose that \((t',q')=(0,0) \) and that \( (t,q)~\text {lies}~ \text {in} \overline{{\textrm{dom}}(\partial _{\textsf{q}}{{\mathcal {E}}})}^{{\textrm{w,S}}} {{\setminus }} {\textrm{dom}}(\partial _{\textsf{q}}{{\mathcal {E}}})\), so that \({\mathfrak {M}}_{0}^{\alpha }(t,q, t',q') =0\). We observe that there exists a sequence \((t_n,q_n)_n \subset {\textrm{dom}}(\partial _{\textsf{q}}{{\mathcal {E}}})\) with \((t_n,q_n) \rightharpoonup (t,q)\) and \(\sup _{n} {\mathfrak {E}}(q_n)<\infty \). We will show that for every null sequence \((\varepsilon _k)_{k\in {\mathbb {N}}}\) there exists a recovery sequence for (t, q, 0, 0). For this, we first fix \(n\in {\mathbb {N}}\) and associate with \((t_n,q_n, 0, 0)\) the recovery sequence \((t_{\varepsilon _k,n}, q_{\varepsilon _k,n}, t_{\varepsilon _k,n}', q_{\varepsilon _k,n}') = (t_n,q_n,t_{\varepsilon _k,n}', 0)\), where we choose \( t'_{\varepsilon _k,n}>0\) such that
Setting \(n=k\) we obtain the sequence \(({\tilde{t}}_{\varepsilon _k}, {\tilde{q}}_{\varepsilon _k}, {\tilde{t}}_{\varepsilon _k}', {\tilde{q}}_{\varepsilon _k}')= (t_k,q_k, t'_{\varepsilon _k,k}, 0) \rightharpoonup (t,q,0,0)\), which gives (i). We also have \(\sup _{k\in {\mathbb {N}}}{\mathfrak {E}}( {\tilde{q}}_{\varepsilon _k})\le \sup _{n\in {\mathbb {N}}} {\mathfrak {E}}( q_n) <\infty \), which gives (ii). Moreover, because of \( {\tilde{t}}_{\varepsilon _k}'> 0\) and \({{\tilde{q}}}'_{\varepsilon _k}=0\) we have
Thus, condition (iii) in (5.10b) holds as well. With this, Proposition 5.2 is established. \(\square \)
For later use we also introduce the ‘reduced’ rescaled joint M-function
We observe that the dissipation potentials \(\psi _{\textsf{u}}: = {{\mathcal {V}}}_{\textsf{u}}\) and \(\psi _{{\textsf{z}}}: ={{\mathcal {R}}}{+} {{\mathcal {V}}}_{\textsf{z}}\) have rate-independent parts null and equal to \({{\mathcal {R}}}\), respectively, and that \({\mathfrak {b}}_{\psi _{{\textsf{z}}}} = {{\mathcal {R}}}+ {\mathfrak {b}}_{{{\mathcal {V}}}_{\textsf{z}}}\) thanks to (4.2b). Thus, from (5.7) and Proposition 3.7 we infer that the following representation formula for \( {\mathfrak {M}}_{0}^{\alpha ,{\textrm{red}}}\) holds:
for \(\partial _{\textsf{q}}{{\mathcal {E}}}(t,q) = \varnothing \) we have
The expressions in (5.12) reflect the fact that \({\mathfrak {M}}_{\varepsilon }^{\alpha }\) only depends on the three cases given by \(\alpha \in (0,1)\), \(\alpha =1\), or \(\alpha >1\).
We emphasize that \( {\mathfrak {M}}_{0}^{\alpha ,{\textrm{red}}}\) depends on \({{\mathcal {R}}}\) as well, namely through \({\mathscr {S}}_{\textsf{z}}^*\) which is defined via \({\mathcal {W}}_{\textsf{z}}^*\). In particular, for \(t'>0\) finiteness of \( {\mathfrak {M}}_{0}^{\alpha ,{\textrm{red}}}(t,q, t',q')\) enforces that \(0={\mathscr {S}}_{\textsf{u}}^*(t,q) = {\mathscr {S}}_{\textsf{z}}^*(t,q) \) and hence, taking into account Hypothesis 4.10,
In the specific cases of the dissipation potentials \({{\mathcal {V}}}_{\textsf{u}}\) and \({{\mathcal {V}}}_{\textsf{z}}\) considered in Example 3.5, we even have the explicit expression of the respective contact potentials \({\mathfrak {b}}_{{{\mathcal {V}}}_{\textsf{u}}}\) and \({\mathfrak {b}}_{{{\mathcal {V}}}_{\textsf{z}}}\), and thus of the (reduced) rescaled joint M-function \({\mathfrak {M}}_{0}^{\alpha ,{\textrm{red}}}\). In particular, let us revisit the p-homogeneous case:
Example 5.3
(The p-homogeneous case) Suppose that the dissipation potentials \({{\mathcal {V}}}_{\textsf{u}}\) and \({{\mathcal {V}}}_{\textsf{z}}\) are positively p-homogeneous with the same \(p\in (1,\infty )\). Then, combining (3.12) with (5.12) we conclude that for \(t'=0\) and \(\partial _{\textsf{q}}{{\mathcal {E}}}(t,q) \ne \varnothing \) we have (where \({\hat{c}}_p = p^{1/p} (p')^{1/p'}\))
The M-functions \( {\mathfrak {M}}_{\varepsilon }^{\alpha }\) enjoy suitable coercivity properties that will play a key role in the compactness arguments for proving the existence of \(\text {BV}\) solutions. These estimates are direct consequences of the the lower bounds on \({\mathfrak {B}}^\alpha _\varepsilon \) derived in Lemma 3.8 and the definition of \({\mathfrak {M}}_{\varepsilon }^{\alpha }\). The importance here is the uniformity in \(\varepsilon \in [0,1]\).
We also emphasize that we are stating a result that is focusing on \(z'\) and ignoring \(u'\), which reflects the fact that we always assume the bound on \(\Vert u'_\varepsilon \Vert _{{\textrm{L}}^1(0,T;{\textbf{U}})}\) whereas for \(z'_\varepsilon \) we only have a bound in \({\textrm{L}}^1(0,T;{\textbf{Z}}_{{\textrm{ri}}})\), but we need the derivative \({\textsf{z}}'(s)\in {\textbf{Z}}\) at least in points where \({\mathscr {S}}_{\textsf{z}}^*({\textsf{t}}(s),{\textsf{q}}(s))>0\).
Lemma 5.4
The following estimates hold for all \(c>0\) and \(\varepsilon \in [0,1]\) with \(\varkappa \) from Lemma 3.8:
The proof of (5.15a) and (5.15b) follows directly from the definition of \({\mathfrak {M}}_{\varepsilon }^{\alpha }\) and the corresponding estimates (3.17b) and (3.17e) for \({\mathfrak {B}}^\alpha _\varepsilon \) in Lemma 3.8, respectively.
The following result is an immediate consequence of the definition of \({\mathfrak {M}}_{\varepsilon }^{\alpha }\) and of Proposition 3.2(b5), if we recall the definitions of \({\mathfrak {A}}_{\textsf{x}}^{*,0}\) from (4.21).
Lemma 5.5
For all \(\alpha >0\) and all \(\varepsilon \in [0,1]\) we have that

for all \((t,q,t',q') \in [0,T]{\times }{\textbf{Q}}{\times }[0,\infty ) {\times }{\textbf{Q}}\) and all \(\xi = (\mu ,\zeta ) \in {\mathfrak {A}}_{\textsf{u}}^{*}(t,q), \, \zeta \in {\mathfrak {A}}_{\textsf{z}}^{*}(t,q)\).
5.2 Admissible Parametrized Curves
The concept of admissible parametrized curve is tailored in such a way that it is able to describe limiting curves \(({\textsf{t}},{\textsf{q}}):[a,b]\rightarrow [0,T]{\times }{\textbf{Q}}\) of a family of parametrized viscous curves \(({\textsf{t}}_\varepsilon ,{\textsf{q}}_\varepsilon )_{\varepsilon }\) satisfying
Since Proposition 5.2 guarantees that \({\mathfrak {M}}_{0}^{\alpha }\) is the \(\Gamma \)-limit of \({\mathfrak {M}}_{\varepsilon }^{\alpha }\) it seems natural that such curves can be characterized by the condition
However, this expression is not well-defined, since we are not able to define the derivatives \({\textsf{q}}'(s)=({\textsf{u}}'(s),{\textsf{z}}'(s))\) almost everywhere. This is due to the fact that \({{\mathcal {R}}}\) is coercive only with respect to the \({\textbf{Z}}_{{\textrm{ri}}}\)-norm. Hence, (5.17) just gives that z is absolutely continuous with values in (the possibly non-reflexive space) \({\textbf{Z}}_{{\textrm{ri}}}\): in particular, z needs not be differentiable with respect to time.
To reformulate (5.17) in a proper way, we take advantage of the special form of \({\mathfrak {M}}^{\alpha ,{\textrm{red}}}_0\) given in (5.12) by observing that \({\textsf{z}}'(s)\) is only needed on the special sets \({\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\) to be defined below. Hence, condition (5.17) can be replaced by (5.21) in Definition 5.6 ahead, where the pointwise derivative \(z'\) is replaced by a scalar surrogate, cf. (5.19) below, whose definition involves the dissipation potential \({{\mathcal {R}}}\) and generalizes the concept of metric derivative from the theory of gradient flows in metric spaces [3].
-
(1)
We say that a curve \(z: [a,b]\rightarrow {\textbf{Z}}\) is \({{\mathcal {R}}}\)-absolutely continuous if there exists a nonnegative function \(m \in {\textrm{L}}^1(a,b)\) such that
$$\begin{aligned} {{\mathcal {R}}}( z(s_2) {-} z(s_1) ) \le \int _{s_1}^{s_2} m(s) \,\,\!{\textrm{d}}s \quad \text {for every}\quad a\le s_1\le s_2 \le b, \end{aligned}$$(5.18)and we denote by \({\textrm{AC}}([a,b];{\textbf{Z}},{{\mathcal {R}}})\) the space of \({{\mathcal {R}}}\)-absolutely continuous curves.
-
(2)
For a curve \(z \in {\textrm{AC}}([a,b];{\textbf{Z}},{{\mathcal {R}}})\) we set
$$\begin{aligned} {{\mathcal {R}}}[z'](s): = \lim _{h\rightarrow 0} {{\mathcal {R}}}\Big ( \frac{1}{h} \big ( z(s{+}h)- z(s)\big ) \Big ) \quad \text {for a.a. }\, s \in (a,b). \end{aligned}$$(5.19)
The notation \( {\textrm{AC}}([a,b];{\textbf{Z}},{{\mathcal {R}}})\) encodes the fact that, while the curves z take values in \({\textbf{Z}}\), their absolute continuity depends on the dissipation potential \({{\mathcal {R}}}\) which only controls the weaker norm \(\Vert \cdot \Vert _{{\textbf{Z}}_{{\textrm{ri}}}}\). We are now in a position to give our definition of admissible parametrized curve, which adapts [42, Def. 4.1] to the present multi-rate system. We recall that the slope functions \({\mathscr {S}}_{\textsf{x}}^*\) are lsc according to Hypothesis 4.10. Hence, along continuous curves \(({\textsf{t}},{\textsf{q}}):[a,b]\rightarrow [0,T]{\times }{\textbf{Q}}\) the following sets are relatively open:
The difference between the cases \(\alpha > 1\) and \(\alpha \in (0,1)\) in the definition of the set \( {\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\) is commented after the following definition.
Definition 5.6
(\({{\mathscr {A}}([a,b];[0,T]{\times }{\textbf{Q}})}\)) A curve \(({\textsf{t}},{\textsf{q}}) =: [a,b] \rightarrow [0,T]{\times }{\textbf{Q}}\) with q = (u, z) is called an admissible parametrized curve if
-
(1)
\({\textsf{t}}\) is non-decreasing, \(({\textsf{t}},{\textsf{u}})\in \textrm{AC}([a,b];\mathbb {R}\times \textbf{U}),\,\textsf{z} \in \textrm{AC}([a,b];\,{{\textbf{Z}}}_\textrm{ri},{{\mathcal {R}}})\);
-
(2)
\({\mathscr {S}}_{\textsf{u}}^*({\textsf{t}},{\textsf{q}}) = 0\) and \({\mathscr {S}}_{\textsf{z}}^*({\textsf{t}},{\textsf{q}}) = 0\) on the set \(\left\{ \, s \in (a,b) \, \big | \, {\textsf{t}}'(s) >0 \,\right\} \);
-
(3)
\({\textsf{z}}\) is locally \({\textbf{Z}}\)-absolutely continuous on the open set \( {\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\), and \({\textsf{t}}\) is constant on every connected component of \({\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\);
-
(4)
\( \sup _{s\in [a,b]}{\mathfrak {E}}({\textsf{q}}(s)) \le E\) for some \(E>0\);
-
(5)
It holds that
$$\begin{aligned} \int _{a}^{b} {{\mathcal {R}}}[{\textsf{z}}'](s) \,\,\!{\textrm{d}}s + \int _{{\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]} {\mathfrak {M}}_{0}^{\alpha ,{\textrm{red}}}({\textsf{t}}(s),{\textsf{u}}(s),{\textsf{z}}(s),0,{\textsf{u}}' (s),{\textsf{z}}' (s)) \,\,\!{\textrm{d}}s <\infty . \end{aligned}$$(5.21)
We will denote by \({\mathscr {A}}([a,b];[0,T]{\times }{\textbf{Q}})\) the collection of all admissible parametrized curves from [a, b] to \([0,T]{\times }{\textbf{Q}}\). Furthermore, we say that \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}}([a,b];[0,T]{\times }{\textbf{Q}})\) is
-
non-degenerate, if
$$\begin{aligned} {\textsf{t}}'(s) + {{\mathcal {R}}}[{\textsf{z}}'](s) + \Vert {\textsf{u}}'(s)\Vert _{\textbf{U}}>0 \quad \text {for a.a.}\; s\in (a,b); \end{aligned}$$(5.22) -
surjective, if \({\textsf{t}}(a) =0\) and \({\textsf{t}}(b)=T\).
Finally, in the case in which the function \({\textsf{t}}\), defined on the canonical interval [0, 1], is constant with \({\textsf{t}}(s) \equiv t\) for some \(t\in [0,T]\), we call \({\textsf{q}}\) an admissible transition curve between \(q_0:=q(0)\) and \(q_1: = q(1)\) at time t, and we will use the notation
The requirement that \({\textsf{z}}\) has to be locally \({\textbf{Z}}\)-absolutely continuous on the set \({\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\), and the different definition of \({\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\) in the cases \(\alpha \ge 1\) and \(\alpha \in (0,1)\), are clearly motivated by properties (5.15) (which, in turn, derive from Lemma 3.8). Indeed, in the case \(\alpha \in (0,1)\), in view of (5.15a), once \({\mathfrak {M}}_{0}^{\alpha }({\textsf{t}},{\textsf{q}}, {\textsf{t}}',{\textsf{q}}')\) is estimated and \({\mathscr {S}}_{\textsf{z}}^*({\textsf{t}},{\textsf{q}})\) is strictly positive, then \({\mathfrak {M}}_{0}^{\alpha }({\textsf{t}},{\textsf{q}}, {\textsf{t}}',{\textsf{q}}')\) provides a control on \(\Vert {\textsf{z}}'\Vert _{{\textbf{Z}}}\). Because of this, parametrized curves are required to be absolutely continuous on the set \({\mathscr {S}}_{\textsf{z}}^*({\textsf{t}},{\textsf{q}})>0\). In the case \(\alpha \ge 1\), in view of estimate (5.15b), the z-component of admissible parametrized curves is expected to be absolutely continuous on the larger set where \({\mathscr {S}}_{\textsf{u}}^*({\textsf{t}},{\textsf{q}})+{\mathscr {S}}_{\textsf{z}}^*({\textsf{t}},{\textsf{q}})>0\).
Hence, on the one hand, in (5.21) we integrate only over the set \({\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\), because it is in \({\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\) where the pointwise derivative \({\textsf{z}}' \in {\textbf{Z}}\) exists, which makes the term \({\mathfrak {M}}_{0}^{\alpha ,{\textrm{red}}}({\textsf{t}}(s),{\textsf{q}}(s), 0,{\textsf{q}}'(s) )\) well defined. On the other hand, the specific form of \({\mathfrak {M}}_{0}^{\alpha ,{\textrm{red}}}\) in (5.12) and the fact that \({\mathfrak {b}}_\psi (v,0)=0\) for all v show that \(\textsf{z}' \in {\textbf{Z}}\) is only needed on the set \({\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\).
Remark 5.7
In principle, for admissible parametrized curves \(({\textsf{t}},{\textsf{u}},{\textsf{z}})\), it would be sufficient that \({\textsf{u}}\) is locally absolutely continuous on \({\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\), only, and that \({\textsf{u}}:[a,b] \rightarrow {\textbf{U}}\) is continuous. Nonetheless, for the sake of simplicity we prefer not to weaken Definition 5.6 in this direction.
Hereafter, along an admissible parametrized curve \(({\textsf{t}},{\textsf{q}})\) we shall use the notation
with \( {{\mathcal {R}}}[{\textsf{z}}'] \) from (5.19) and \({\varvec{1}}_{{\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]}\) the indicator function of the set \({\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\). Let us stress that the above notation makes sense only along an admissible curve. If the admissible curve \(({\textsf{t}},{\textsf{q}})\) has the additional property \({\textsf{z}}\in {\textrm{AC}}([a,b];{\textbf{Z}})\) and thus \({\textsf{z}}'(s)\) is well defined as an element of \({\textbf{Z}}\) for almost all \(s\in (a,b)\), then \( {{\mathcal {R}}}[z'](s)= {{\mathcal {R}}}(z'(s)) \) a.e. in (a, b). Hence, for an admissible curve with \({\textsf{z}}\in {\textrm{AC}}([a,b];{\textbf{Z}})\) we have \( {\mathfrak {M}}_0^\alpha [{\textsf{t}},{\textsf{q}},{\textsf{t}}',{\textsf{q}}'] (s) = {\mathfrak {M}}_0^\alpha ({\textsf{t}}(s),{\textsf{q}}(s),{\textsf{t}}'(s),{\textsf{q}}'(s)) \ \text {for a.a. }s \in (a,b). \)
5.3 Definition of Parametrized Balanced-Viscosity Solutions
We are now in a position to precisely define parametrized Balanced-Viscosity (\(\text {pBV}\)) solutions to the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\), see Definition 5.10. At the core of this concept there lies a (parametrized) chain-rule inequality, cf. Hypothesis 5.8 that will be imposed as an additional property of the rate-independent system, while Proposition 5.17 will provide sufficient conditions for the validity of Hypothesis 5.8.
We will also introduce an enhanced version of the \(\text {pBV}\) concept, in which we additionally require z to be absolutely continuous with values in \({\textbf{Z}}\). In [42, Sec. 4.2] this notion had been already introduced, using a different terminology that might create slight confusion in the present multi-rate context and has thus been changed here. We believe the enhanced concept to be significant as well because, for some examples (cf. e.g. the applications discussed in Sect. 8), the vanishing-viscosity analysis will directly lead to enhanced BV solutions.
The definition of \(\text {pBV}\) solutions relies on the validity of the following assumption on the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\):
Hypothesis 5.8
(Chain rule along admissible parametrized curves) For every admissible parametrized curve \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}} ([a,b];[0,T]{\times }{\textbf{Q}})\)
Remark 5.9
In general, the chain-rule inequality (5.24) along a given admissible parametrized curve \(({\textsf{t}},{\textsf{q}})\) does not follow from the chain rule of Hypothesis 4.7, because for these curves the pointwise derivative \({\textsf{z}}'\) exists as an element in \({\textbf{Z}}\) only on the set \({\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\) from (5.20). That is why, Proposition 5.17 provides a sufficient condition under which Hypothesis 4.7 ensures the validity of Hypothesis 5.8, albeit restricted to admissible curves satisfying additionally \({\textsf{z}}\in {\textrm{AC}}([a,b];{\textbf{Z}})\).
We are now ready to introduce the exact notion of \(\text {pBV}\) solutions.
Definition 5.10
(\(\text {pBV}\) and enhanced \(\text {pBV}\) solutions) Assume Hypotheses 4.1, 4.2, 4.3, 4.5, and 4.10, and let the system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) satisfy Hypothesis 5.8. We call a curve \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}} ([a,b];[0,T]{\times }{\textbf{Q}})\) a parametrized Balanced-Viscosity (\(\text {pBV}\)) solution to the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) if \(({\textsf{t}},{\textsf{q}})\) satisfies the parametrized energy-dissipation balance
for every \( a \le s_1 \le s_2\le b\), where \({\mathfrak {M}}_0^\alpha \) is defined in (5.23).
A \(\text {pBV}\) solution \(({\textsf{t}},{\textsf{q}})=({\textsf{t}},{\textsf{u}},{\textsf{z}})\) is called enhanced \(\text {pBV}\) solution, if additionally \({\textsf{z}}\in {\textrm{AC}}([a,b];{\textbf{Z}})\).
For an enhanced \(\text {pBV}\) solution \(({\textsf{t}},{\textsf{q}})\) we have \({\textsf{q}}\in {\textrm{AC}}([a,b];{\textbf{Q}})\), since \({\textsf{q}}\in {\mathscr {A}} ([a,b];[0,T]{\times }{\textbf{Q}})\) already implies \({\textsf{u}}\in {\textrm{AC}}([a,b];{\textbf{U}})\). As a consequence of the chain-rule inequality (5.24) from Hypothesis 5.8, we have the following characterization:
Lemma 5.11
(Characterization of \(\text {pBV}\) solutions) Let Hypothesis 5.8 hold additionally. Then for an admissible parametrized curve \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}} ([a,b];[0,T]{\times }{\textbf{Q}})\), the following three properties are equivalent:
-
(1)
\(({\textsf{t}},{\textsf{q}}) \) is a \(\text {pBV}\) solution of the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\);
-
(2)
\(({\textsf{t}},{\textsf{q}}) \) fulfills the upper energy estimate \(\le \) in (5.25) on for \(s_1=a\) and \(s_2=b\);
-
(3)
\(({\textsf{t}},{\textsf{q}}) \) fulfills the pointwise identity for a.a. \(s\in (a,b)\)
$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}s} {\mathcal {E}}({\textsf{t}}(s),{\textsf{q}}(s)) - \partial _t {\mathcal {E}}({\textsf{t}}(s),{\textsf{q}}(s)) {\textsf{t}}'(s) =- {\mathfrak {M}}_0^\alpha [{\textsf{t}},{\textsf{q}},{\textsf{t}}',{\textsf{q}}'](s) . \end{aligned}$$(5.26)
The proof is a simple adaptation of the arguments for [39, Prop. 5.3] and [42, Cor 3.5] and is thus omitted.
5.4 Existence Results for \(\text {pBV}\) Solutions
Our first main result states that any family \(({\textsf{t}}_\varepsilon ,{\textsf{u}}_\varepsilon ,{\textsf{z}}_\varepsilon )_\varepsilon \) obtained by suitably rescaling (cf. Remark 5.16 ahead) a family of solutions to the viscous system (1.4), and satisfying the key a priori estimate (5.29), converges along a subsequence, as \(\varepsilon \rightarrow 0^+\), to a parametrized solution of the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\). We stress that, a bound for the first three terms in (5.29) easily follows by reparametrizing the basic energy estimates for the viscous solutions \((u_\varepsilon ,z_\varepsilon )\), cf. Lemma 4.12. A bound for the fourth term \(\Vert {\textsf{u}}_\varepsilon '\Vert _{{\textbf{U}}}\) is obtained by reparametrizing the non-trivial bound
which we will assume for all our existence results. In fact, (5.27) can be proved under additional conditions on the coupling between the variables u and z, see Proposition 4.13 for an abstract approach and Proposition 8.4 for the concrete application to a delamination model.
Theorem 5.12
(Existence of \(\text {pBV}\) solutions) Under Hypotheses 4.1, 4.2, 4.3, 4.5,4.10, and 5.8, let \((q_{\varepsilon _k})_k = (u_{\varepsilon _k}, z_{\varepsilon _k})_k \subset {\textrm{AC}}([0,T]; {\textbf{Q}})\) be a sequence of solutions to the generalized viscous gradient system (1.4) with \((\varepsilon _k)_k \subset (0,\infty )\) a null sequence. Suppose that
for some \(q_0=(u_0,z_0) \in {\mathscr {D}}\). Let \({\textsf{t}}_{\varepsilon _k}: [0,{{{\textsf{S}}}}]\rightarrow [0,T]\) be non-decreasing surjective time-rescalings such that \({\textsf{q}}_{\varepsilon _k} = ({\textsf{u}}_{\varepsilon _k},{\textsf{z}}_{\varepsilon _k})\) defined via \({\textsf{q}}_{\varepsilon _k}(s)=q_{\varepsilon _k}({\textsf{t}}_{\varepsilon _k}(s))\) satisfies the crucial bound
Then, there exist a (not relabeled) subsequence and a curve \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}}([0,{{{\textsf{S}}}}]; [0,T]{\times }{\textbf{Q}})\) such that
-
(1)
$$\begin{aligned}&{\textsf{t}}\in {\textrm{C}}_{{\textrm{lip}}}^0 ([0,{{{\textsf{S}}}}]; [0,T]), \quad {\textsf{q}}= ({\textsf{u}},{\textsf{z}}) \in {\textrm{C}}_{{\textrm{weak}}}^0([0,{{{\textsf{S}}}}]; {\textbf{U}}_{{\textrm{e}}}{\times }{\textbf{Z}}_{{\textrm{e}}}),\nonumber \\&{\textsf{u}}\in {\textrm{C}}_{{\textrm{lip}}}^0 ([0,{{{\textsf{S}}}}];{\textbf{U}}), \quad {\textsf{z}}\in {\textrm{C}}_{{\textrm{lip}}}^0 ([0,{{{\textsf{S}}}}];{\textbf{Z}}_{{\textrm{ri}}}) \cap {\textrm{C}}^0([0,{{{\textsf{S}}}}];{\textbf{Z}}); \end{aligned}$$(5.30)
-
(2)
the following convergences hold as \(k\rightarrow \infty \)
$$\begin{aligned}&{\textsf{t}}_{\varepsilon _k} \rightarrow {\textsf{t}}\text { in } {\textrm{C}}^0([0,{{{\textsf{S}}}}]), \end{aligned}$$(5.31a)$$\begin{aligned} \quad&{\textsf{u}}_{\varepsilon _k}\overset{*}{\rightharpoonup }{\textsf{u}}\text { in } W^{1,\infty } (0,{{{\textsf{S}}}};{\textbf{U}}),{} & {} {\textsf{z}}_{\varepsilon _k}\rightarrow {\textsf{z}}\text { in } {\textrm{C}}^0 ([0,{{{\textsf{S}}}}];{\textbf{Z}}), \end{aligned}$$(5.31b)$$\begin{aligned}&{\textsf{u}}_{\varepsilon _k}(s) \rightharpoonup {\textsf{u}}(s) \text { in } {\textbf{U}}_{{\textrm{e}}}\ \text {and}{} & {} {\textsf{z}}_{\varepsilon _k}(s) \rightharpoonup {\textsf{z}}(s) \text { in } {\textbf{Z}}_{{\textrm{e}}}\qquad \text { for all } s \in [0,{{{\textsf{S}}}}]; \quad \end{aligned}$$(5.31c) -
(3)
\(({\textsf{t}},{\textsf{q}})\) fulfills the upper energy-dissipation estimate \( \le \) in (5.25) on \([0,{{{\textsf{S}}}}]\), hence \(({\textsf{t}},{\textsf{q}})\) is a \(\text {pBV}\) solution to the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\).
Moreover, \(({\textsf{t}},{\textsf{u}},{\textsf{z}})\) is surjective and there hold the additional convergences
for all \(0\le s_1\le s_2 \le {{{\textsf{S}}}}\).
We postpone the proof of Theorem 5.12 to Sect. 7.2, but point out here that the core of the limit passage in the parametrized energy-dissipation estimate (5.4), leading to (5.25), lies in the following straightforward consequence of Ioffe’s theorem [19] (see also [60, Thm. 21]). A ‘metric version’ of Proposition 5.13 below was proved in [38, Lemma 3.1].
Proposition 5.13
Let \({\textbf{S}}\) be a weakly closed subset of \({\textbf{Q}}\), and let \(({\mathscr {M}}_\varepsilon )_{\varepsilon }, \, {\mathscr {M}}_0: {\mathbb {R}}{\times }{\textbf{S}}{\times }{\mathbb {R}}{\times }{\textbf{Q}}\rightarrow [0,\infty ]\) be measurable and weakly lower semicontinuous functionals fulfilling the \(\Gamma \)-\(\liminf \) estimate
Suppose that, for \(\varepsilon \ge 0\), the functional \({\mathscr {M}}_\varepsilon (t,q,\cdot ,\cdot )\) is convex for every \((t,q) \in {\mathbb {R}}{\times }{\textbf{S}}\). Let \(({\textsf{t}}_\varepsilon , {\textsf{q}}_\varepsilon ), \, ({\textsf{t}},{\textsf{q}}) \in {\textrm{AC}}([a,b]; {\mathbb {R}}{\times }{\textbf{S}})\) fulfill
Then,
Proof
It is sufficient to introduce the functional \(\bar{{\mathscr {M}}}:{\mathbb {R}}{\times }{\textbf{S}}{\times }{\mathbb {R}}{\times }{\textbf{Q}}{\times }[0,\infty ] \rightarrow [0,\infty ]\) defined by
and to observe that \({\mathscr {M}}\) is lower semicontinuous with respect to the weak topology of \({\mathbb {R}}{\times }{\textbf{S}}{\times }{\mathbb {R}}{\times }{\textbf{Q}}{\times }[0,\infty ]\) and convex for every \((t,q) \in {\mathbb {R}}{\times }{\textbf{Q}}\) and \(\varepsilon \ge 0\). Then, by Ioffe’s theorem we conclude that
i.e., (5.35) is established. \(\square \)
Remark 5.14
Theorem 5.12 does not guarantee that the \(\text {pBV}\) solution is non-degenerate even if the quantity in (5.29) has a uniform positive lower bound. Nonetheless, any (possibly degenerate) solution \(({\textsf{t}},{\textsf{q}})\) can be reparametrized to a non-degenerate one \(({\widetilde{{\textsf{t}}}},{\widetilde{{\textsf{q}}}}): [0,{\widetilde{{{{\textsf{S}}}}}}]\rightarrow [0,T]{\times }{\textbf{Q}}\), fulfilling
For this, we proceed as in [14] and associate with \(({\textsf{t}},{\textsf{q}})\) the rescaling function \({\widetilde{\sigma }}\) defined by \({\widetilde{\sigma }}(s) = \int _0^s ( {\textsf{t}}'(r) {+} {{\mathcal {R}}}[{\textsf{z}}'](r) {+} \Vert {\textsf{u}}'(r)\Vert _{\textbf{U}}) \,\,\!{\textrm{d}}r \) and set \({\widetilde{{{{\textsf{S}}}}}} = \sigma ({{{\textsf{S}}}})\). We then define \(({\widetilde{{\textsf{t}}}}(\sigma ),{\widetilde{{\textsf{q}}}}(\sigma )): = ({\textsf{t}}(s),{\textsf{q}}(s)) \) for \(\sigma = {\widetilde{\sigma }}(s)\). The very same calculations as in [30, Lem. 4.12] (or based on the reparametrization result [3, Lem. 1.1.4]), yield (5.36).
Our next result, whose proof is omitted (cf. also Remark 5.16), addresses the existence of enhanced \(\text {pBV}\) solutions which, again, is obtained under the crucial assumption of the \({\textrm{L}}^1\)-bound (5.27).
Theorem 5.15
(Existence of enhanced \(\text {pBV}\) solutions) Assume Hypotheses 4.1, 4.2, 4.3, 4.5, 4.10, and 5.8. Suppose that there exist rescaled solutions \(({\textsf{t}}_{\varepsilon _k},{\textsf{q}}_{\varepsilon _k})_k\) to the viscous system (1.4)\(_{\varepsilon _k}\) such that, in addition to (5.29), there also holds the estimate
Then, up to a (not relabeled) subsequence the curves \(({\textsf{t}}_{\varepsilon _k},{\textsf{q}}_{\varepsilon _k})_k\) converge to an admissible parametrized curve \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}}([0,{{{\textsf{S}}}}]; [0,T]{\times }{\textbf{Q}})\) such that (5.30), (5.31), (5.32) hold and additionally \( {\textsf{z}}\in {\textrm{C}}_{{\textrm{lip}}}^0 ([0,{{{\textsf{S}}}}];{\textbf{Z}})\), i.e., \(({\textsf{t}},{\textsf{q}})\) is an enhanced \(\text {pBV}\) solution to the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\).
Remark 5.16
In the statement of Theorem 5.12, the reparametrization \(t={\textsf{t}}_{\varepsilon _k}(s)\) yielding the rescaled solutions \({\textsf{q}}_{\varepsilon _k}\) can be chosen arbitrarily, provided it guarantees the Lipschitz bound (5.29). Under Hypotheses 4.1, 4.2 and 4.3, all viscous solutions \((u_{\varepsilon _k},z_{\varepsilon _k})\) satisfy the uniform bound \(\Vert z'_{\varepsilon _k}\Vert _{{\textrm{L}}^1(0,T;{\textbf{Z}}_{{\textrm{ri}}})}\le C\), see (4.26). If, additionally \(\Vert u'_{\varepsilon _k}\Vert _{{\textrm{L}}^1(0,T;{\textbf{Z}}_{{\textrm{ri}}})}\le C\) holds (for instance, under the additional conditions (4.27) and (4.28), which guarantee estimate (4.29) in Corollary 4.13), then a reparametrization yielding (5.29) is easily obtained, for instance, by using the energy-dissipation arclength in (5.2).
Similarly, under the stronger a priori estimate
one easily obtains rescaled solutions satisfying the stronger Lipschitz bound (5.37). Hence, one gains enhanced compactness information for the sequence \(({\textsf{z}}_{\varepsilon _k})_k\), and the proof of Theorem 5.12 immediately yields a proof of Theorem 5.15.
We conclude this section with some sufficient conditions for the validity of (a stronger form of) the parametrized chain rule in Hypothesis 5.8. It will be derived as a consequence of the non-parametrized chain rule in Hypothesis 4.7.
Proposition 5.17
(Sufficient conditions for parametrized chain rule) Assume that Hypothesis 4.7 holds and that the vanishing-viscosity contact potentials associated with \({{\mathcal {V}}}_{\textsf{u}}\) and \({{\mathcal {V}}}_{\textsf{z}}\) satisfy
for \({\textsf{x}}\in \{ {\textsf{u}},{\textsf{z}}\}\) and \({\textbf{X}}\in \{ {\textbf{U}},{\textbf{Z}}\}\) (see the discussion around (3.9)).
Then, the parametrized chain rule (5.24) holds along all admissible curves \( ({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}} ([a,b];[0,T]{\times }{\textbf{Q}})\) with \({\textsf{q}}\in {\textrm{AC}}([a,b];{\textbf{Q}})\). In particular, we have

for all measurable selections \( (a,b) \ni s \mapsto (\mu (s),\zeta (s) ) \in {\textbf{U}}^*{\times }{\textbf{Z}}^*\) satisfying for almost all \(s\in (a,b)\) \( (\mu (s),\zeta (s) ) \in {\mathfrak {A}}_{\textsf{u}}^{*}({\textsf{t}}(s),{\textsf{q}}(s)) {\times }{\mathfrak {A}}_{\textsf{z}}^{*}({\textsf{t}}(s),{\textsf{q}}(s)) \).
The proof will be carried out in Appendix A.
5.5 Differential Characterization of Enhanced \(\text {pBV}\) Solutions
The main result of this section is Theorem 5.21, which provides a further characterization of enhanced \(\text {pBV}\) solutions in terms of solutions of a system of subdifferential inclusions, see (5.48). This differential form has the very same structure as the viscous system (4.13), except that the small parameters \(\varepsilon ^\alpha \) and \(\varepsilon \) multiplying the viscous terms are replaced by coefficients \(\lambda _{\textsf{u}}\) and \(\lambda _{\textsf{z}}\) satisfying the switching conditions (5.49c). For this, we use the optimality in the energy-dissipation balance.
In Lemma 5.5 we have established the estimate

which is valid for all \((t,q,t',q') \in [0,T]{\times }{\textbf{Q}}{\times }[0,\infty ) {\times }{\textbf{Q}}\) and which is a generalization of the classical Young–Fenchel inequality  . With the first result of this section we will show that, in analogy to the characterization of generalized gradient-flow equations via the energy-dissipation principle, we are able to characterize \(\text {pBV}\) solutions via the optimality condition that estimate (5.41) holds as an equality. Thus, we define the contact set \(\Sigma _\alpha \) (cf. [41, Def. 3.6]) via
. With the first result of this section we will show that, in analogy to the characterization of generalized gradient-flow equations via the energy-dissipation principle, we are able to characterize \(\text {pBV}\) solutions via the optimality condition that estimate (5.41) holds as an equality. Thus, we define the contact set \(\Sigma _\alpha \) (cf. [41, Def. 3.6]) via

Proposition 5.18 below makes the relation between enhanced \(\text {pBV}\) solutions and the contact set \( \Sigma _\alpha \) rigorous. We emphasize here that we need to exploit the stronger version (5.40) of the parametrized chain rule from Hypothesis 5.8, in addition to Hypotheses 4.1, 4.2, 4.3, 4.5, and 4.10, always tacitly assumed. Recall that a sufficient condition for such a chain rule is provided by Proposition 5.17.
Proposition 5.18
(Enhanced \(\text {pBV}\) solutions lie in \(\Sigma _\alpha \)) Suppose that the parametrized chain rule (5.40) holds along all admissible curves \( ({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}} ([a,b];[0,T]{\times }{\textbf{Q}})\) with \({\textsf{q}}\in {\textrm{AC}}([a,b];{\textbf{Q}})\). Then, a curve \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}} ([a,b];[0,T]{\times }{\textbf{Q}})\) is an enhanced \(\text {pBV}\) solution of \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) if and only if \({\textsf{q}}\in {\textrm{AC}}([a,b];{\textbf{Q}})\) and \(({\textsf{t}},{\textsf{q}},{\textsf{t}}',{\textsf{q}}')\in \Sigma _\alpha \) a.e. in (a, b).
Proof
Let us consider an admissible parametrized curve \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}} ([a,b];[0,T]{\times }{\textbf{Q}})\) with \({\textsf{q}}\in {\textrm{AC}}([a,b];{\textbf{Q}})\). By the characterization provided in Lemma 5.11, \(({\textsf{t}},{\textsf{q}})\) is a \(\text {pBV}\) solution if and only if \( - {\mathfrak {M}}_0^\alpha ({\textsf{t}},{\textsf{q}},{\textsf{t}}',{\textsf{q}}') = \frac{{\textrm{d}}}{{\textrm{d}}s} {\mathcal {E}}({\textsf{t}},{\textsf{q}})- \partial _t {\mathcal {E}}({\textsf{t}},{\textsf{q}}) {\textsf{t}}' \) almost everywhere in (a, b). Combining this with the chain-rule inequality (5.40) we in fact conclude that

for all measurable selections \( \xi =(\mu ,\zeta ): (a,b) \rightarrow {\mathfrak {A}}_{\textsf{u}}^{*}({\textsf{t}}(s),{\textsf{q}}(s)) {\times }{\mathfrak {A}}_{\textsf{z}}^{*}({\textsf{t}}(s),{\textsf{q}}(s)) \), hence \(({\textsf{t}},{\textsf{q}},{\textsf{t}}',{\textsf{q}}')\in \Sigma _\alpha \) a.e. in (a, b). The converse implication follows by the same argument. \(\square \)
The final step in relating enhanced \(\text {pBV}\) solutions to the solutions of the sub-differential system (5.48) is obtained by analyzing the structure of \(\Sigma _\alpha \). For this, we exploit the exact form of \({\mathfrak {M}}_{0}^{\alpha }\) and use the definition of the set \({\mathfrak {A}}_{\textsf{x}}^{*}(t,q) \) in terms of the Fréchet subdifferential \(\partial _{\textsf{x}}{{\mathcal {E}}}(t,q)\), \({\textsf{x}}\in \{{\textsf{u}}, {\textsf{z}}\}\). To formulate this properly, we recall the definition of the rescaled viscosity potentials \({{\mathcal {V}}}_{\textsf{x}}^{\lambda }\) and their subdifferentials \(\partial {{\mathcal {V}}}_{\textsf{x}}^{\lambda }\) from (1.5) for \(\lambda \in [0,\infty ]\). In particular, we have

Observe that, thanks to (4.2b) we have \(\partial {{\mathcal {V}}}_{\textsf{x}} (0) = \{ 0 \}\) for \({\textsf{x}}\in \{{\textsf{u}},{\textsf{z}}\}\).
We now consider the system of subdifferential inclusions for the quadruple \((t,q,t',q')= (t,u,z, t',u',z')\) including the two parameters \(\lambda _{\textsf{u}}, \lambda _{\textsf{z}} \in [0,\infty ]\):



Here we use the usual convention \(\infty /(1{+}\infty )=1\) and emphasize that, at this stage, system (5.44) is not to be understood as a system of subdifferential inclusions. Instead, \((t',q')\in [0,\infty ){\times } {\textbf{Q}}\) are treated as independent variables. With this we are able to introduce the following subsets of \([0,T]{\times }{\textbf{Q}}{\times }[0,\infty ) {\times }{\textbf{Q}}\), called evolution regimes, thus providing a basis for the informal discussion at the end of Sect. 2:
The letters \({\textrm{E}}, \, {\textrm{R}},\, {\textrm{V}},\, {\textrm{B}} \), stand for Equilibrated, Rate-independent, Viscous, and Blocked, respectively. We will discuss the meaning of the names of the evolution regimes below. It will be efficient to use the notation
nonetheless, note that the set \( {\textrm{V}}_{\textsf{uz}} \) is different from (indeed, strictly contained in) \({\textrm{V}}_{\textsf{u}} {\textrm{V}}_{\textsf{z}} \). We also remark that any set involving ‘V’ of ‘B’ is necessarily restricted to the subspace with \(t'=0\) because of (5.44c). With this, we are now in a position to state our result for the contact sets \(\Sigma _\alpha \), under the additional condition (4.23) on the product form of the Fréchet subdifferential \(\partial _q{{\mathcal {E}}}\). Proposition 5.19 below will be proven in Sect. 7.3.
Proposition 5.19
(\(\Sigma _\alpha \) and evolution regimes) If, in addition, the Fréchet subdifferential \(\partial _q {{\mathcal {E}}}\) has the product structure (4.23), then we have the following inclusions for the contact set \( \Sigma _\alpha \):
where in all cases the three sets on the right-hand side are disjoint.
Remark 5.20
In the characterization of (enhanced) \(\text {pBV}\) solution provided by Proposition 5.18, the contact condition  holds for all
holds for all  . Hence, it seems possible to define a smaller contact set \({\widetilde{\Sigma }}_\alpha \) by replacing “\(\exists \)” in (5.42) by “\(\forall \)”. Because of \({\widetilde{\Sigma }}_\alpha \subset \Sigma _\alpha \) inclusions (5.46) would remain true. However, using our larger set \(\Sigma _\alpha \) is sufficient to deduce that \(\text {pBV}\) solutions satisfy the system of subdifferential inclusions (5.48) ahead.
. Hence, it seems possible to define a smaller contact set \({\widetilde{\Sigma }}_\alpha \) by replacing “\(\exists \)” in (5.42) by “\(\forall \)”. Because of \({\widetilde{\Sigma }}_\alpha \subset \Sigma _\alpha \) inclusions (5.46) would remain true. However, using our larger set \(\Sigma _\alpha \) is sufficient to deduce that \(\text {pBV}\) solutions satisfy the system of subdifferential inclusions (5.48) ahead.
The different evolution regimes characterized by the right-hand sides in (5.46) can be visualized by considering the three real parameters \((t',\lambda _{\textsf{u}}, \lambda _{\textsf{z}})\in [0,\infty ){\times } [0,\infty ]^2\), since the rate-independent regimes \({\textrm{E}}_{\textsf{u}}\) and \({\textrm{R}}_{\textsf{z}}\) are given by \(\lambda _{\textsf{u}}=0\) and \(\lambda _{\textsf{z}}=0\) respectively. Similarly, the viscous regimes \({\textrm{V}}_{\textsf{x}}\), \({\textsf{x}} \in \{ {\textsf{u}}, {\textsf{z}}\}\), are defined via \(\lambda _{\textsf{x}}\in (0,\infty )\), and the blocking regime \({\textrm{B}}_{\textsf{x}}\) is determined by \(\lambda _{\textsf{x}}=\infty \). The sets on the right-hand sides in (5.46) are then defined in terms of the switching conditions
The corresponding sets in the \((t',\lambda _{\textsf{u}},\lambda _{\textsf{z}})\) space are depicted in Fig. 1.
The switching conditions and the different regimes are displayed in the space for \((t',\lambda _{\textsf{u}},\lambda _{\textsf{z}}) \in [0,\infty ]^3\). For \({\textsf{t}}'>0\) the different admissible regimes depend on \({\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}}={\textrm{E}}_{\textsf{u}} \cap {\textrm{R}}_{\textsf{z}}\). For \({\textsf{t}}'=0\) the different admissible regimes depend on \(\alpha >0\): for \(\alpha >1\) one has \({\textrm{E}}_{\textsf{u}} \cup {\textrm{B}}_{\textsf{z}}\), for \(\alpha =1\) one has \({\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}} \cup {\textrm{V}}_{\textsf{uz}}\cup {\textrm{B}}_{\textsf{u}} {\textrm{B}}_{\textsf{z}}\) , and for \(\alpha \in (0,1)\) one has \({\textrm{V}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}} \cup {\textrm{B}}_{\textsf{u}}\)
The inclusions (5.46) that relate the contact sets to the different evolution regimes \({\textrm{A}}_{\textsf{u}} {\textrm{C}}_{\textsf{z}}\) have a clear and immediate interpretation in terms of the evolutionary behavior of an enhanced \(\text {pBV}\) solution \(({\textsf{t}}, {\textsf{q}})\):
-
\({\textrm{E}}_{\textsf{u}}\) encodes the regime where \(u={\textsf{u}}(s)\) stays in equilibria, which may depend on s. Indeed, inserting \(\lambda _{\textsf{u}}(s)=0\) in (5.44a) leads to the equilibrium condition \(0 \in \partial _{\textsf{u}}{{\mathcal {E}}}({\textsf{t}}(s),{\textsf{q}}(s))\). This means that \({\textsf{u}}(s)\) follows \({\textsf{z}}(s)\) that may evolve rate-independently when \(t'>0\), and may follow a viscous jump path, or may be blocked, when \({\textsf{t}}'(s)=0\).
-
\({\textrm{R}}_{\textsf{z}}\) denotes the rate-independent evolution for \({\textsf{z}}(s)\), where \(\lambda _{\textsf{z}}(s)=0\). The component \({\textsf{u}}(s)\) either follows staying in equilibria, evolves viscously, or is blocked.
-
In the case \(t'>0\) only the rate-independent regime \({\textrm{E}}_{\textsf{u}}{\textrm{R}}_{\textsf{z}}\) is admissible. This is the regime with \(\lambda _{\textsf{u}}=\lambda _{\textsf{z}}=0\) where the viscous dissipation potentials \({{\mathcal {V}}}_{\textsf{u}}\) and \({{\mathcal {V}}}_{\textsf{z}}\) do not come into action.
-
In the regime \({\textrm{V}}_{\textsf{x}}\), the variable \({\textsf{x}}(s)\) evolves viscously with \(\lambda _{\textsf{x}}(s)\in (0,\infty )\), and necessarily \({\textsf{t}}'(s)=0\).
-
\({\textrm{V}}_{\textsf{uz}}\) is the special case occurring only for \(\alpha =1\), where \(\lambda _{\textsf{u}}(s)=\lambda _{\textsf{z}}(s)\in (0,\infty )\), i.e. both components have a synchronous viscous phase.
-
The blocked regime \({\textrm{B}}_{\textsf{x}}\), occurring when \({\textsf{t}}'(s)=0\), encodes the situation that \(\lambda _{\textsf{x}}(s)=\infty \), which means that on the given time scale the viscosity is so strong that the \({\textsf{x}}\)-component cannot move, i.e. it is blocked with \({\textsf{x}}'(s)=0\).
-
\({\textrm{B}}_{\textsf{uz}} = {\textrm{B}}_{\textsf{u}} {\textrm{B}}_{\textsf{z}}\) means that both components are blocked, namely \({\textsf{q}}'(s)=0\). This can occur, for instance, if we set \(({\textsf{t}}(s), {\textsf{q}}(s))=(t_*,q_*)\) for \(s\in (s_1,s_2)\). Then, \(\lambda _{\textsf{u}}(s)=\lambda _{\textsf{z}}(s)=\infty \) still gives a trivial, constant solution. Such a behavior may occur after taking a limit like \(\varepsilon \rightarrow 0^+\), but of course the interval can be cut out by defining a \(\text {pBV}\) solution on \([0,{{{\textsf{S}}}}{-}s_2{+}s_1]\).
We are now in a position to prove a characterization of enhanced \(\text {pBV}\) solutions in terms of the following system of subdifferential inclusions
where the balanced interplay of viscous and rate-independent behavior in the equations for u and z, respectively, is determined by the (arclength-dependent) parameters \(\lambda _{\textsf{u}}(s)\) or \(\lambda _{\textsf{z}}(s)\). We emphasize that the so-called switching conditions for \(t'\ge 0\) and \(\lambda _{\textsf{u}}, \,\lambda _{\textsf{z}} \in [0,\infty ]\), cf. (5.49c) below, are different for the three cases \(\alpha >1\), \(\alpha =1\), and \(\alpha \in (0,1)\).
Theorem 5.21
(Differential characterization of enhanced \(\text {pBV}\) solutions) Assume Hypotheses 4.1, 4.2, 4.3, 4.5, and 4.10 and let the parametrized chain rule (5.40) hold. In addition, suppose that the Fréchet subdifferential \(\partial _q {{\mathcal {E}}}\) has the product structure from (4.23). Let \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}}([0,{{{\textsf{S}}}}];[0,T]{\times }{\textbf{Q}})\) be an admissible parametrized curve with \({\textsf{q}}\in {\textrm{AC}}([0,{{{\textsf{S}}}}];{\textbf{Q}})\).
-
(1)
If \(({\textsf{t}},{\textsf{q}}):(0,{{{\textsf{S}}}})\rightarrow {\textbf{Q}}\) is a enhanced \(\text {pBV}\) solution of \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\), then there exist measurable functions \((\lambda _{\textsf{u}},\lambda _{\textsf{z}}): (0,{{{\textsf{S}}}})\rightarrow [0,\infty ]^2 \) and \(\xi =(\mu ,\zeta ): (0,{{{\textsf{S}}}})\rightarrow {\textbf{U}}^*{\times }{\textbf{Z}}^*\) with
$$\begin{aligned} \mu (s) \in \partial _{\textsf{u}}{{\mathcal {E}}}({\textsf{t}}(s),{\textsf{u}}(s), {\textsf{z}}(s)) \; \text {and} \; \zeta (s) \in \partial _{\textsf{z}}{{\mathcal {E}}}({\textsf{t}}(s),{\textsf{u}}(s), {\textsf{z}}(s)) \quad \text {for a.a. }\, s \in (0,{{{\textsf{S}}}}) \end{aligned}$$(5.49a)satisfying for almost all \(s\in (0,{{{\textsf{S}}}})\) the subdifferential inclusions
$$\begin{aligned} \begin{aligned}&-\mu (s) \in \partial {{\mathcal {V}}}_{\textsf{u}}^{\lambda _{\textsf{u}}(s)} ( {\textsf{u}}'(s))\qquad \qquad \qquad \qquad \text {in}\; {\textbf{U}}^*,\\&- \zeta (s) \in \partial {{\mathcal {R}}}({\textsf{z}}'(s)) + \partial {{\mathcal {V}}}_{\textsf{z}}^{\lambda _{\textsf{z}}(s)} ( {\textsf{z}}'(s)) \quad \text {in}\; {\textbf{Z}}^*, \end{aligned} \end{aligned}$$(5.49b)and the switching conditions
$$\begin{aligned} {\textsf{t}}'(s)\,\frac{\lambda _{\textsf{u}}(s)}{1{+}\lambda _{\textsf{u}}(s) } = 0 = {\textsf{t}}'(s) \frac{\lambda _{\textsf{z}}(s)}{1{+}\lambda _{\textsf{z}}(s)} \quad \text {and} \quad {\left\{ \begin{array}{ll} \lambda _{\textsf{u}}(s)\frac{1}{1{+}\lambda _{\textsf{z}}(s)} =0 &{} \text {for}\;\alpha >1,\\ \lambda _{\textsf{u}}(s) = \lambda _{\textsf{z}}(s)&{} \text {for}\;\alpha =1,\\ \frac{1}{1{+}\lambda _{\textsf{u}}(s)}\lambda _{\textsf{z}}(s)=0&{} \text {for}\; \alpha \in (0,1). \end{array}\right. } \end{aligned}$$(5.49c) -
(2)
Conversely, if there exist measurable functions \((\lambda _{\textsf{u}},\lambda _{\textsf{z}}): (0,{{{\textsf{S}}}})\rightarrow [0,\infty ]^2 \) and \(\xi =(\mu ,\zeta ): (0,{{{\textsf{S}}}})\rightarrow {\textbf{U}}^*{\times }{\textbf{Z}}^*\) satisfying (5.49) and, in addition,
$$\begin{aligned}{} & {} \sup _{s \in (0,{{\mathsf{{S}}}})} |{{\mathcal {E}}}({\textsf{t}}(s),{\textsf{q}}(s))|<\infty , \quad \text {and} \quad \nonumber \\{} & {} \quad \int _0^{{{\mathsf{{S}}}}} \!\big ( \Vert \mu (s)\Vert _{{\textbf{U}}^*} \Vert {\textsf{u}}'(s)\Vert _{{\textbf{U}}} {+} \Vert \zeta (s)\Vert _{{\textbf{Z}}^*} \Vert {\textsf{z}}'(s)\Vert _{{\textbf{Z}}} \big ) \,\,\!{\textrm{d}}s <\infty , \end{aligned}$$(5.50)then \(({\textsf{t}},{\textsf{q}})\) is an enhanced \(\text {pBV}\) solution.
Proof
Part (1) basically follows from combining the characterization of enhanced \(\text {pBV}\) solutions from Proposition 5.18 in terms of the contact set, with Proposition 5.19. Only the measurability of the coefficients \(\lambda _{\textsf{u}},\, \lambda _{\textsf{z}}: [0,{{{\textsf{S}}}}]\rightarrow [0,\infty ] \) and of the selections \(\xi =(\mu ,\zeta ):(0,{{{\textsf{S}}}}) \rightarrow {\textbf{U}}^* {\times }{\textbf{Z}}^*\) deserves some discussion that is postponed to Appendix B.
Let us now carry out the proof of Part (2). After cutting out possible intervals where \(({\textsf{t}},{\textsf{q}})\) may be constant (i.e. in the blocking regime \({\textrm{B}}_{\textsf{u}} {\textrm{B}}_{\textsf{z}}\)), we may suppose that the admissible parametrized curve \(({\textsf{t}},{\textsf{q}})\) fulfills the non-degeneracy condition (5.22). In what follows, we will use the short-hand notation
for \({\mathrm {A \in \{E,V,B\}}} \) and \( {\mathrm {C \in \{R,V,B\}} }\). We will discuss at length the case \(\alpha >1\); the very same arguments yield the thesis also in the cases \(\alpha =1\) and \(\alpha \in (0,1)\). It follows from the switching conditions (5.49c) that the integral  decomposes as \(I= I_1+I_2+I_3\) with
decomposes as \(I= I_1+I_2+I_3\) with

where we use that the three regimes \( {\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}}\), \( {\textrm{E}}_{\textsf{u}}{\textrm{V}}_{\textsf{z}}\), and \({\textrm{B}}_{\textsf{z}}\) are disjoint. Now, on \((0,{{{\textsf{S}}}}) \cap {\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}}\) we have that \(\mu (s) \equiv 0\), while \(\zeta (s) \in \partial {{\mathcal {R}}}({\textsf{z}}'(s))\), so that
where we used (5.11) and (5.12), taking into account \({\mathscr {S}}_{\textsf{u}}^*({\textsf{t}}(s),{\textsf{q}}(s)) = {\mathscr {S}}_{\textsf{z}}^*({\textsf{t}}(s),{\textsf{q}}(s)) \equiv 0\) on \((0,{{{\textsf{S}}}}) \cap {\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}}\). On \((0,{{{\textsf{S}}}}) \cap {\textrm{E}}_{\textsf{u}}{\textrm{V}}_{\textsf{z}}\) we have \({\mathscr {S}}_{\textsf{u}}^*({\textsf{t}}(s),{\textsf{q}}(s)) \equiv 0\) and the z-equation in (5.48) holds with \(\lambda _{\textsf{z}}(s)>0\), so that

where (1) follows from (5.49b)via Fenchel-Moreau conjugation, (2) is a consequence of the definition of \({\mathscr {S}}_{\textsf{z}}^*({\textsf{t}},{\textsf{q}})\), (3) is due to the definition of \( {\mathfrak {b}}_{{{\mathcal {V}}}_{\textsf{z}}}\), and (4) again ensues from (5.11) and (5.12). Finally, with the very same arguments we find that
Combining the above estimates with (5.52) and with the chain-rule (4.16) (which applies thanks to (5.50)), we ultimately conclude that

namely \(({\textsf{t}},{\textsf{q}})\) fulfills the upper energy-dissipation estimate. Therefore, by Lemma 5.11 we conclude that \(({\textsf{t}},{\textsf{q}})\) is an (enhanced) \(\text {pBV}\) solution. \(\square \)
6 True Balanced-Viscosity Solutions
This section is devoted to the the concept of true Balanced-Viscosity (\(\text {BV}\)) solutions, i.e. solutions defined on the original time interval [0, T] instead via the artificial arc length \(s \in [0,{{{\textsf{S}}}}]\). This concept will be introduced in Sect. 6.1 in Definition 6.5. The central ingredient in this notion is a Finsler-type transition cost that measures the energy dissipated at jumps of the curve (u, z), see Definition 6.2. In Sect. 6.2 we will gain further insight into the fine properties of true \(\text {BV}\) solutions, while Sect. 6.3 states our two existence results, Theorems 6.8 and 6.12, in which \(\text {BV}\) solutions to the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) are obtained by taking the vanishing-viscosity limit of system (1.4) in the real process time, without reparametrization. Section 6.4 addresses the non-parametrized counterpart of enhanced \(\text {pBV}\) solutions called enhanced \(\text {BV}\) solutions, and Sect. 6.5 provides how parametrized and true \(\text {BV}\) solutions are related.
We start with some notations for functions having well-defined jumps.
Notation 6.1
(Weakly regulated functions) Given a Banach space \({\textbf{B}}\), we denote by
the space of (everywhere defined) weakly regulated functions on [0, T] with values in \({\textbf{B}}\), where we use \({f}(0^-):= f(0)\) and \({f}(T^+): = f(T)\). The symbol \(\textrm{BV}([0,T];{\textbf{B}})\) denotes the space of everywhere defined functions of bounded \({\textbf{B}}\)-variation such that \(\textrm{BV}([0,T];{\textbf{B}}) \subset {\textrm{R}}_{\textrm{w}}([0,T];{\textbf{B}})\) with continuous embedding.
Note that for \(f \in {\textrm{R}}_{\textrm{w}}([0,T];{\textbf{B}})\) the three values \(f(t^-)\), f(t), \(f(t^+)\) may all be different for \(t\in (0,T)\), and that distinguishing these values will be crucial for our notion of \(\text {BV}\) solutions.
For a given \(z\in \textrm{BV}([0,T];{\textbf{Z}}_{{\textrm{ri}}})\) we also introduce the \({{\mathcal {R}}}\)-variation
for \( [a,b]\subset [0,T]\), and we observe that
We mention in advance that true \(\text {BV}\) solutions are curves \(q=(u,z)\), with \(u\in \textrm{BV}([0,T];{\textbf{U}})\) and \(z\in {\textrm{R}}_{\textrm{w}}([0,T];{\textbf{Z}}) \cap \textrm{BV}([0,T];{\textbf{Z}}_{{\textrm{ri}}})\). For such \(q=(u,z)\) we introduce the jump set
we record that \( {\textrm{J}}[q]\) consists of at most countably many points. Note that for \( {\textrm{J}}[z]\) the left and the right limits are considered with respect to the norm topology of \({\textbf{Z}}\). For later use, we finally observe that
which can be easily checked exploiting the (compact) embeddings \({\textbf{Z}}_{{\textrm{e}}}\Subset {\textbf{Z}}\subset {\textbf{Z}}_{{\textrm{ri}}}\). Note that in \(\textrm{BV}([0,T]; {\textbf{Z}}_{{\textrm{ri}}})\) the left and right limits \(z(t^\pm )\) are strong limits in \({\textbf{Z}}_{{\textrm{ri}}}\), while in \({\textrm{R}}_{\textrm{w}}([0,T];{\textbf{Z}}_{{\textrm{e}}})\) they are weak limits in \({\textbf{Z}}_{{\textrm{e}}}\).
6.1 Definition of True \(\text {BV}\) Solution
The (possibly asymmetric) Finsler cost function is obtained by minimizing an ‘infinitesimal cost’, depending on the fixed process time \(t\in [0,T]\) and defined in terms of the rescaled joint M-function \( {\mathfrak {M}}_{0}^{\alpha }\), along admissible transition curves \({\textsf{q}}: [0,1] \rightarrow {\textbf{Q}}\). From now on, for better clarity we will denote a generic transition curve by  in place of \({\textsf{q}}\).
in place of \({\textsf{q}}\).
Definition 6.2
(Admissible transition curves, Finsler cost) For given \(t\in [0,T]\) and \(q_0=(u_0,z_0), q_1=(u_1,z_1) \in {\textbf{U}}{\times }{\textbf{Z}}\), we define the Finsler cost induced by \({\mathfrak {M}}_{0}^{\alpha }\) by

with the short-hand notation \({\mathfrak {M}}_{0}^{\alpha }[\cdot ,\cdot ,\cdot ,\cdot ]\) from (5.23) and \({\mathcal {A}}_{t}(q_0,q_1)\) the set of all admissible transition curves at time t between \(q_0\) and \(q_1\), see Definition 5.6.
Thanks to the 1-positive homogeneity of the functional  , we observe that it is not restrictive to suppose that all transition curves are defined on [0, 1].
, we observe that it is not restrictive to suppose that all transition curves are defined on [0, 1].
We are now ready to define a new variation called the \({\mathfrak {M}}_{0}^{\alpha }\)-total variation of a curve \(q=(u,z):[0,T]\rightarrow {\textbf{Q}}\). It consists, cf. (6.8) below, of the \({{\mathcal {R}}}\)-variation of z as defined in (6.2) plus extra contributions at jump points \(t_*\in {\textrm{J}}(q)\) that may arise through rate-independent or viscous transition costs between \({q}(t_*^-)\), \(q(t_*)\), and \({q}(t_*^+)\). These extra contributions are given by the Finsler cost (6.6), from which the \({{\mathcal {R}}}\)-variation is subtracted to avoid that it is counted twice in the \({\mathfrak {M}}_{0}^{\alpha }\)-variation. The resulting terms are positive because we always have \({\textrm{cost}}_{{\mathfrak {M}}_{0}^{\alpha }}(t;(u_0,z_0),(u_1,z_1)) \ge {{\mathcal {R}}}(z_1{-}z_0)\) since \( {\mathfrak {M}}_{0}^{\alpha }[t,q,0,q'] \ge {{\mathcal {R}}}(z')\) (using \({\mathfrak {M}}_{0}^{\alpha ,{\textrm{red}}}(t,q, 0,q')\ge 0\)).
Definition 6.3
(\({\mathfrak {M}}_{0}^{\alpha }\)-variations) Let \(q =(u,z):[0,T] \rightarrow {\textbf{Q}}\) with \(u \in \textrm{BV}([0,T];{\textbf{U}}) \) and \(z\in {\textrm{R}}_{\textrm{w}}([0,T];{\textbf{Z}}){\cap } \) \( \textrm{BV}([0,T];{\textbf{Z}}_{{\textrm{ri}}}) \) be a curve with \(\sup _{t\in [0,T]} {\mathfrak {E}}(q(t)) \le E <\infty \) and jump set \({\textrm{J}}[q]\). For closed subintervals \([a,b]\subset [0,T]\) we define
-
(1)
the extra Viscous Jump Variation of q induced by \({\mathfrak {M}}_{0}^{\alpha }\) on [a, b] via
$$\begin{aligned} {\textrm{eVJV}}_{{\mathfrak {M}}_{0}^{\alpha }}(q;[a,b])&:= \big ( {\textrm{cost}}_{{\mathfrak {M}}_{0}^{\alpha }}(a;q(a),{q}(a^+)) -{{\mathcal {R}}}({z}(a^+){-} z(a))\big )\nonumber \nonumber \\&\quad + \!\! \sum _{t \in {\textrm{J}}[q]\cap (a,b)} \!\! \big ({\textrm{cost}}_{{\mathfrak {M}}_{0}^{\alpha }}(t;{q}(t^-),q(t)) -{{\mathcal {R}}}(z(t){-} {z}(t^-)) \nonumber \\&\qquad \qquad \qquad \quad +{\textrm{cost}}_{{\mathfrak {M}}_{0}^{\alpha }}(t;q(t) ,{q}(t^+) ) -{{\mathcal {R}}}({z}(t^+){-} z(t))\big )\nonumber \\&\quad + \big ({\textrm{cost}}_{{\mathfrak {M}}_{0}^{\alpha }}(b;{q}(b^-),q(b)) -{{\mathcal {R}}}(z(b){-} {z}(b^-))\big ) ; \end{aligned}$$(6.7) -
(2)
the \({\mathfrak {M}}_{0}^{\alpha }\)-total variation
$$\begin{aligned} {\textrm{Var}}_{{\mathfrak {M}}_{0}^{\alpha }}(q;[a,b]): = {\textrm{Var}}_{{{\mathcal {R}}}}(z;[a,b]) + {\textrm{eVJV}}_{{\mathfrak {M}}_{0}^{\alpha }}(q;[a,b]). \end{aligned}$$(6.8)
Indeed, in the above definition we could drop the condition that \(z\in {\textrm{R}}_{\textrm{w}}([0,T];{\textbf{Z}})\), since the conditions \(\sup _{t\in [0,T]} {\mathfrak {E}}(q(t)) \le E <\infty \) and \( z \in \textrm{BV}([0,T];{\textbf{Z}}_{{\textrm{ri}}}) \) even ensure that \(z\in {\textrm{R}}_{\textrm{w}}([0,T];{\textbf{Z}}_{{\textrm{e}}})\), cf. (6.5). In what follows, we will thus omit that requirement whenever it is redundant. With slight abuse of notation, here we will use the symbol \( {\textrm{Var}}_{{\mathfrak {M}}_{0}^{\alpha }}\) for the \({\mathfrak {M}}_{0}^{\alpha }\)-total variation, although this is not a standard form of total variation, cf. [39, Rem. 3.5].
Just as for its parametrized counterpart, our definition of (true) \(\text {BV}\) solutions will rely on a suitable chain-rule requirement, enhancing Hypothesis 4.7 to curves \(q=(u,z)\) having just a \({\textrm{BV}}\)-time regularity. For consistency, we will formulate this \({\textrm{BV}}\)-chain rule as a hypothesis.
Hypothesis 6.4
(Chain rule in BV) For every curve \(q=(u,z):[0,T]\rightarrow {\textbf{Q}}\) with \(u \in \textrm{BV}([0,T];{\textbf{U}})\) and \(z \in {\textrm{R}}([0,T];{\textbf{Z}}) {\cap }\) \( \textrm{BV}([0,T];{\textbf{Z}}_{{\textrm{ri}}})\) and satisfying
the following chain-rule estimate holds, for all closed subset \([t_0,t_1] \subset [0,T]\):
In Lemma A.2 in Appendix A we to show that the parametrized chain rule from Hypothesis 5.8 also guarantees the validity of Hypothesis 6.4. Hence, subsequently we will directly assume Hypothesis 5.8.
Let us now give our definition of \(\text {BV}\) solutions \(q:[0,T]\rightarrow {\textbf{U}}{\times }{\textbf{Z}}\), i.e. \(\text {BV}\) solutions without parametrization. We sometimes use the word ‘true \(\text {BV}\) solution’ to distinguish \(\text {BV}\) solutions from ‘parametrized \(\text {BV}\) solutions’, hence there is no difference between \(\text {BV}\) solutions and true \(\text {BV}\) solutions. Definition 6.5 below is a natural extension of the concept of \(\text {BV}\) solutions introduced in [42, Def. 3.10], now taking care of the equilibrium condition (6.10a) for u corresponding to the regime \({\textrm{E}}_{\textsf{u}}\), the local stability condition (6.10b) for z corresponding to the regime \({\textrm{R}}_{\textsf{z}}\), and an energy-dissipation balance (6.10c). Hence, all jump behavior is compressed into the definition of the Finsler cost \({\textrm{cost}}_{{\mathfrak {M}}_{0}^{\alpha }}\), the total \({\mathfrak {M}}_{0}^{\alpha }\)-variation, and the validity of the energy-dissipation balance.
Definition 6.5
(True \(\text {BV}\) solutions) Let the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) fulfill Hypothesis 6.4. A curve \(q=(u,z):[0,T]\rightarrow {\textbf{Q}}\) is called a true Balanced-Viscosity solution to \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) if satisfies the following conditions:
-
\(u \in {\textrm{BV}}([0,T];{\textbf{U}})\) and \(z \in \textrm{BV}([0,T];{\textbf{Z}}_{{\textrm{ri}}}) \);
-
the stationary equation
$$\begin{aligned} {\mathscr {S}}_{\textsf{u}}^*(t,q(t))=0 \quad \text {for all}\; t \in [0,T]{\setminus } {\textrm{J}}[q]; \end{aligned}$$(6.10a) -
the local stability condition
$$\begin{aligned} {\mathscr {S}}_{\textsf{z}}^*(t,q(t))=0 \quad \text {for all}\; t \in [0,T]{\setminus } {\textrm{J}}[q]; \end{aligned}$$(6.10b) -
the energy-dissipation balance
$$\begin{aligned}&{\mathcal {E}}(t,q(t)) + {\textrm{Var}}_{{\mathfrak {M}}_{0}^{\alpha }}(q;[s,t]) \nonumber \\&\quad = {\mathcal {E}}(s,q(s)) + \int _s^t \partial _t {\mathcal {E}}(r,q(r)) \,\,\!{\textrm{d}}r \quad \text {for}\; 0\le s\le t \le T. \end{aligned}$$(6.10c)
Again, observe that for any Balanced-Viscosity solution one in fact has \(z\in {\textrm{R}}_{\textrm{w}}([0,T];{\textbf{Z}}_{{\textrm{e}}})\).
We postpone to Sect. 6.4 a result comparing parametrized and true \(\text {BV}\) solutions. With the exception of our existence results Theorems 6.8 and 6.12, in the following statements we will omit to explicitly recall the assumptions of Sect. 4; we will only invoke the chain rule from Hypothesis 5.8.
6.2 Characterization and Fine Properties of \(\text {BV}\) Solutions
In the same way as for their parametrized version, thanks to the chain rule (6.9) we have a characterization of \(\text {BV}\) solutions in terms of the upper energy estimate \(\le \) in (4.18), on the whole interval [0, T]. We also have a second characterization in terms of a simple energy-dissipation balance like for energetic solutions as in [12, 29, 33, 34], combined with jump conditions that balance the different dissipation mechanics that may be active at a jump point. The proof of Proposition 6.6 follows, with minimal changes, from the arguments for [42, Cor. 3.14, Thm. 3.15], to which the reader is referred.
Proposition 6.6
Let the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) fulfill Hypothesis 5.8. For a curve \(q=(u,z) \in \textrm{BV}([0,T];{\textbf{U}}) {\times }\textrm{BV}([0,T];{\textbf{Z}}_{{\textrm{ri}}}) \) fulfilling the stationary equation (6.10a) and the local stability (6.10b), the following three assertions are equivalent:
-
(1)
q is a true \(\textrm{BV}\) solution of system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\);
-
(2)
q fulfills
$$\begin{aligned} {\mathcal {E}}(T,q(T)) + {\textrm{Var}}_{{\mathfrak {M}}_{0}^{\alpha }}(q;[0,T]) \le {\mathcal {E}}(0,q(0)) + \int _0^T \partial _t {\mathcal {E}}(r,q(r)) \,\,\!{\textrm{d}}r;\nonumber \\ \end{aligned}$$(6.11) -
(3)
q fulfills the \({{\mathcal {R}}}\)-energy-dissipation inequality
$$\begin{aligned} {\mathcal {E}}(t,q(t)) + {\textrm{Var}}_{{{\mathcal {R}}}}(q;[s,t]) \le {\mathcal {E}}(s,q(s)) + \int _s^t \partial _t {\mathcal {E}}(r,q(r)) \,\,\!{\textrm{d}}r \end{aligned}$$(6.12)with \({\textrm{Var}}_{{\mathcal {R}}}\) from (6.2), and the jump conditions at every \(t\in {\textrm{J}}[q]:\)
$$\begin{aligned} {\mathcal {E}}(t,{q}(t^-)) - {\mathcal {E}}(t,q(t))&= {\textrm{cost}}_{{\mathfrak {M}}_{0}^{\alpha }}(t;{q}(t^-),q(t)),\nonumber \\ {\mathcal {E}}(t,q(t)) - {\mathcal {E}}(t,{q}(t^+))&= {\textrm{cost}}_{{\mathfrak {M}}_{0}^{\alpha }}(t;q(t),{q}(t^+)). \end{aligned}$$(6.13)
Conditions (6.13) provide a fine description of the behavior of \(\text {BV}\) solutions (u, z) at jumps. However, the \(\inf \) in the definition of \({\textrm{cost}}_{{\mathfrak {M}}_{0}^{\alpha }}\) need not be attained, as the functional \({\mathfrak {M}}_{0}^{\alpha }\) does not control the norm of the space where we look for the \(\vartheta _{\textsf{u}}\)-component of admissible transition curves. Nonetheless, in certain situations (cf. the proof of Theorem 6.15 below) the existence of transitions attaining the optimal cost will play a key role. In fact, it will be sufficient to require the existence of these curves in cases in which the Finsler cost equals the energy release, which happens at the jump points of a true \(\text {BV}\) solution as in (6.13). That is why, hereafter we will refer to such transitions as optimal jump transitions, a notion that will be made precise in Definition 6.7. Therein we restrict to transition curves, defined on [0, 1], connecting points \(q_-=(u_-,z_-)\) and \(q_+=(u_+,z_+)\) such that the u-components \(u_-\) and \(u_+\) are at equilibrium, and the z-components \(z_-\) and \(z_+\) are locally stable.
Definition 6.7
Given \(t\in [0,T]\) and \(q_-=(u_-,z_-), \, q_+=(u_+,z_+) \in {\textbf{Q}}\) fulfilling \({\mathscr {S}}_{\textsf{u}}^*(t,q_\pm ) = {\mathscr {S}}_{\textsf{z}}^*(t,q_\pm )=0\), we call an admissible curve  an optimal transition between \(q_-\) and \( q_+ \) at time t if it fulfills
an optimal transition between \(q_-\) and \( q_+ \) at time t if it fulfills

Furthermore, we say that  is of
is of
-
sliding type if
 for all \(r\in [0,1]\);
for all \(r\in [0,1]\); -
viscous type if
 for all \(r\in (0,1)\).
for all \(r\in (0,1)\).
Observe that an optimal transition of viscous type can be governed by viscosity either in u, or in z, or in both variables. With the very same argument as for the proof of [42, Prop. 3.19], to which we refer for all details, we can also show that every optimal transition can be decomposed in a canonical way into an (at most) countable collection of sliding and viscous transitions. We also refer to [47, Sec. 2.3] for the concept of so-called two-speed solutions, which are defined in terms of slow rate-independent parts connected by jumps which are themselves a concatenation of at most countable ‘jump resolution maps’.
6.3 Existence of \(\text {BV}\) Solutions
A most interesting feature of \(\text {BV}\) solutions, already observed in [42], is that it is possible to prove their existence by directly taking the vanishing-viscosity limit of the viscous system (4.11), without reparametrization. In the following result, we adopt a slightly different viewpoint and in fact prove that every limit point q (in the sense of pointwise weak convergence) of a sequence of viscous solutions \((q_{\varepsilon _k})_k = (u_{\varepsilon _k},z_{\varepsilon _k})_k\), starting from well-prepared initial data and such that the \(\textrm{BV}([0,T];{\textbf{U}})\)-norm of \((u_{\varepsilon _k})_k\) is a priori bounded (cf. (6.15) below), is in fact a true \(\text {BV}\) solution. In fact, the existence of limit points can be proved, based on the energy estimates from Lemma 4.12 and on (6.15), via a standard compactness argument and the Helly Theorem.
The statement of Theorem 6.8 below mirrors that of Theorem 5.12:
-
First, in the same way as with (5.32) for parametrized solutions, with (6.17b)–(6.17c) ahead we are stating the convergence of the left-hand side terms in the viscous energy-dissipation estimate (4.20)—in particular, (6.17c) ensures the convergence for \(\varepsilon _k \rightarrow 0^+\) of
$$\begin{aligned}&\int _s^t {\mathfrak {M}}_{{\varepsilon _k}}^{\alpha }(r,q_{\varepsilon _k}(r), 1,q_{\varepsilon _k}'(r)) \,\,\!{\textrm{d}}r \nonumber \\&= \int _s^t \left( {{\mathcal {V}}}_{\textsf{u}}^{\varepsilon _k^\alpha }( u_{\varepsilon _k}'(r)) {+} {{\mathcal {R}}}(z_{\varepsilon _k}'(r)) {+} {{\mathcal {V}}}_{\textsf{z}}^{{\varepsilon _k}}( z_{\varepsilon _k}'(r))\right. \nonumber \\&\qquad \qquad \left. + \frac{{\mathscr {S}}_{\textsf{u}}^*(r,q_{\varepsilon _k}(r))}{{\varepsilon _k}^\alpha } {+} \frac{{\mathscr {S}}_{\textsf{z}}^*(r,q_{\varepsilon _k}(r))}{{\varepsilon _k}}\right) \,\,\!{\textrm{d}}r \end{aligned}$$(6.14)to the corresponding terms in the energy-dissipation balance (6.10c). We emphasize here that, for (6.17c) to hold it is crucial that the definition of the total variation functional \({\textrm{Var}}_{{\mathfrak {M}}_{0}^{\alpha }}\), in the general closed subinterval \([s,t] \subset [0,T]\), takes into account the appropriate contributions at the jump points. In particular, we point out that, by (6.7), also the jumps occurring at the extrema s and t are taken into account exactly, in the sense that \({\textrm{cost}}_{{\mathfrak {M}}_{0}^{\alpha }}(s;q(s),q(s^+))=\lim _{\sigma \rightarrow s^+} \lim _{\varepsilon _k\rightarrow 0} \int _0^\sigma {\mathfrak {M}}_{\varepsilon _k}^{\alpha }(\cdot ) \,\,\!{\textrm{d}}r \).
-
Secondly, (6.15) corresponds exactly to the \({\textrm{L}}^1\)-a priori estimate for \(\Vert u_{{\varepsilon _k}}'\Vert _{{\textbf{U}}} \) in (5.27), and to estimate (4.29) established in Proposition 4.13. Sufficient conditions for this estimate have been discussed in Sect. 4.6; alternatively, in concrete examples this estimate could be verified by direct calculations.
Theorem 6.8
(Convergence to \(\text {BV}\) solutions) Let the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) fulfill Hypotheses 4.1, 4.2, 4.3, 4.5, 4.10, and 5.8. For any null sequence \((\varepsilon _k)_k\) let \((q_{\varepsilon _k})_k = (u_{\varepsilon _k},z_{\varepsilon _k})_k \subset {\textrm{AC}}([0,T]; {\textbf{Q}})\) be a sequence of solutions to the generalized gradient system (4.11), such that convergences (5.28) to a pair \((u_0,z_0)\in {\mathscr {D}}\) hold at the initial time \(t=0\), and such that, in addition,
Let \(q:[0,T] \rightarrow {\textbf{Q}}\) be such that, along a not relabeled subsequence, there holds as \(k\rightarrow \infty \)
(every sequence in the above conditions possesses at least one limit point in the sense of (6.16)). Then,
-
(1)
\(q=(u,z) \in \textrm{BV}([0,T];{\textbf{U}}) {\times }\textrm{BV} ([0,T];{\textbf{Z}}_{{\textrm{ri}}})\), and q is a true \(\text {BV}\) solution to the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\);
-
(2)
there hold the additional convergences as \(k\rightarrow \infty \)
$$\begin{aligned}&u_{\varepsilon _k}(t)\rightharpoonup u(t)\;\text {in}\; {\textbf{U}}_{{\textrm{e}}}, \quad z_{\varepsilon _k}(t)\rightharpoonup z(t)\;\text {in}\; {\textbf{Z}}_{{\textrm{e}}}\quad \text {for all}\; t \in [0,\,\,\,T], \end{aligned}$$(6.17a)$$\begin{aligned}&\qquad \qquad \qquad \qquad {\mathcal {E}}(t,q_{\varepsilon _k}(t)) \rightarrow {\mathcal {E}}(t,q(t)) \quad \text {for all}\; t \in [0,T], \end{aligned}$$(6.17b)$$\begin{aligned}&\lim _{k\rightarrow \infty } \int _s^t {\mathfrak {M}}_{{\varepsilon _k}}^{\alpha }(r,q_{\varepsilon _k}(r), 1,q_{\varepsilon _k}'(r)) \,\,\!{\textrm{d}}r = {\textrm{Var}}_{{\mathfrak {M}}_{0}^{\alpha }}(q;[s,t]) \quad \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \text {for all}\;0\le s \le t \le T. \end{aligned}$$(6.17c)
The proof will be carried out in Sect. 7.2.
Remark 6.9
(Vanishing-viscosity approximation versus \(\text {BV}\) solutions) We emphasize that the concept of \(\text {BV}\) solutions enjoys better closedness properties than defining solutions simply as all the limiting points in the vanishing-viscosity approximation. Such solutions are called ‘approximable’ in [30] and there, in Examples 2.5 and 2.6, it is shown in a simple model with \({\textbf{Z}}={\mathbb {R}}\) that there are more \(\text {BV}\) solutions than approximable solutions. It is also made apparent that, for systems with \(\delta \)-dependent energy \({{\mathcal {E}}}_\delta \), approximable solutions \(q^\delta :[0,T]\rightarrow {\mathbb {R}}\) may have a limit \(q^{\delta _*} \) for \(\delta \rightarrow \delta _*\) that is no longer an approximable solution, but \(q^{\delta _*}\) is still a \(\text {BV}\) solution. Thus, \(\text {BV}\) solutions seem to have better stability properties, see e.g. [41, Thm. 4.8].
Remark 6.10
(Existence of \(\text {BV}\) solutions by time discretization) Another interesting feature of true \(\text {BV}\) solutions is that they can be obtained as limits of discrete solutions of the time-incremental scheme
with \(\Psi _{\varepsilon ,\alpha }\) from (1.7), as the viscosity parameter \(\varepsilon \) and the time-step \(\tau \) jointly tend to 0. (Of course, fixing \(\varepsilon >0\) and letting \(\tau \rightarrow 0^+\) in (6.18) gives rise to solutions \(q_\varepsilon :[0,T]\rightarrow {\textbf{Q}}\) of the generalized gradient system (1.6)). This alternative construction of \(\text {BV}\) solutions in the joint discrete-to-continuous and vanishing-viscosity limit of the time-incremental scheme for viscous solutions was carefully explored in [39, Thm. 4.10] and [42, Thm. 3.12]. Following these lines it is possible to show convergence to \(\text {BV}\) solutions along (a subsequence of) any sequence \((\tau _k,\varepsilon _k)\) as long as \(\tau _k\) tends to 0 faster than the time scales in our system, i.e.
To avoid overburdening of the exposition here we refrain from giving a precise convergence statement, but refer to [42, Thm. 3.12], which can adapted to our setup using condition (6.19). The same applies to the convergence of time-discrete solutions to enhanced \(\text {BV}\) solutions introduced below.
6.4 Enhanced \(\text {BV}\) Solutions
This solution concept is to be compared with the notion introduced in [42, Def. 3.21] and, of course, with enhanced \(\text {pBV}\) solutions. In particular, recall that for an enhanced \(\text {pBV}\) solution \(({\textsf{t}},{\textsf{q}}) = ({\textsf{t}}, {\textsf{u}},{\textsf{z}})\) we required the additional regularity \({\textsf{z}}\in {\textrm{AC}}([0,{{{\textsf{S}}}}];{\textbf{Z}})\). Accordingly, an enhanced \(\text {BV}\) solution \(q=(u,z)\) is required to fulfill \(z\in \textrm{BV}([0,T];{\textbf{Z}})\). Moreover, enhanced \(\text {BV}\) solutions enjoy the additional regularity property that at all jump points the left and right limits are connected by optimal transitions with finite length in \({\textbf{U}}{{\times }}{\textbf{Z}}\), such that the total length of the connecting paths \(\vartheta =(\vartheta _{\textsf{u}},\vartheta _{\textsf{z}})\) is finite. In contrast, for general \(\text {BV}\) solutions it is only required that length of the \(\vartheta _{\textsf{u}}\)-component of an optimal jump transition is finite in \({\textbf{U}}\).
Definition 6.11
(Enhanced \(\text {BV}\) solutions) A curve \(q:(u,z):[0,T]\rightarrow {\textbf{Q}}\) is called an enhanced \(\text {BV}\) solution of \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\), if it is a \(\text {BV}\) solution and it satisfies the following additional properties:
-
(i)
\(q\in \textrm{BV}([0,T];{\textbf{Q}}) \);
-
(ii)
for all \(t \in {\textrm{J}}[q]\) there exists an optimal jump transition \(\vartheta ^t = (\vartheta _{\textsf{u}}^t,\vartheta _{\textsf{z}}^t) \in {\mathcal {A}}_{t}({q}(t^-),{q}(t^+)) \) such that \(\vartheta ^t \in {\textrm{AC}}([0,1];{\textbf{Q}})\) and \(q(t)=\vartheta ^t({{\hat{r}}}_t)\) for some \({{\hat{r}}}_t \in [0,1]\);
-
(iii)
\(\sum \limits _{t\in {\textrm{J}}[q]} \int _0^1 \Vert (\vartheta ^t)'(r)\Vert _{{\textbf{Q}}} \,\,\!{\textrm{d}}r = \sum \limits _{t\in {\textrm{J}}[q]} \int _0^1 \left( \Vert (\vartheta _{\textsf{u}}^t)'(r)\Vert _{{\textbf{U}}} {+} \Vert (\vartheta _{\textsf{z}}^t)'(r)\Vert _{{\textbf{Z}}} \right) \,\,\!{\textrm{d}}r <\infty \).
Our existence result for enhanced \(\text {BV}\) solutions can be again proved by our vanishing-viscosity approach without reparametrizing the trajectories, by taking the vanishing-viscosity limit of viscous solutions that satisfy an additional estimate on \(\sup _{k \in {\mathbb {N}}} \Vert z_{\varepsilon _k}\Vert _{\textrm{BV}([0,T];{\textbf{Z}})} \).
Theorem 6.12
(Convergence of viscous solutions to enhanced \(\text {BV}\) solutions) Assume Hypotheses 4.1, 4.2, 4.3, 4.5, 4.10, and 5.8. Let \((q_{\varepsilon _k})_k \subset {\textrm{AC}}([0,T]; {\textbf{Q}})\) be a sequence of solutions to the generalized gradient system (1.4) such that convergences (5.28) hold at \(t=0\), as well as
Let \(q:[0,T]\rightarrow {\textbf{Q}}\) be a limit point for \((q_{\varepsilon _k})_k\) in the sense of (6.16). Then, q is an enhanced \(\text {BV}\) solution of \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\), and the additional convergences (6.17) hold.
Since the proof of Theorem 6.12 follows from combining the argument for Theorem 6.8 with that developed for [42, Thm. 3.22], it is omitted.
6.5 Comparing \(\text {pBV}\) and True \(\text {BV}\) Solutions
In this final subsection we explore the relations between parametrized and true \(\text {BV}\) solutions, also in the enhanced case. Indeed, there is a very natural transition between parametrized and true \(\text {BV}\) solutions. The converse passage will be obtained by ‘filling the graph’ of a true \(\text {BV}\) solution at its jump points, by means of an optimal jump transition, under the additional assumption that it exists. This condition is codified in the following
Hypothesis 6.13
For every \(t\in [0,T]\) and \(q^-, q^+\in {\textbf{Q}}\) such that \({\mathscr {S}}_{\textsf{u}}^*(t,q_\pm ) = {\mathscr {S}}_{\textsf{z}}^*(t,q_\pm )=0\) and
there exists an optimal jump transition  .
.
Remark 6.14
Let us emphasize that Hypothesis 6.13 plays no role in proving the existence of \(\text {BV}\) solutions. It only serves the purpose of showing that a true \(\text {BV}\) solution gives rise to a parametrized one. In this connection, let us mention in advance that, in the statement of Theorem 6.15, Hypothesis 6.13 will not be required for relating enhanced \(\text {BV}\) solutions to their parametrized analogues, as the definition of enhanced \(\text {BV}\) solutions already encompasses the information that optimal jump transitions exist.
We are now ready to state the following relations between true and parametrized \(\text {BV}\) solutions.
Theorem 6.15
(\(\text {pBV}\) versus true \(\text {BV}\) solutions) Let \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) fulfill Hypothesis 5.8. Then the following statements are true:
-
(1)
If \(({\textsf{t}},{\textsf{q}}):[0,{{\mathsf{{S}}}}]\rightarrow [0,T]{\times }{\textbf{Q}}\) is a non-degenerate \(\text {pBV}\) solution of \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) with \({\textsf{t}}(0)=0\) and \({\textsf{t}}({{\mathsf{{S}}}})=T\), then every \(q:[0,T]\rightarrow {\textbf{Q}}\) satisfying
$$\begin{aligned} q(t) \in \left\{ \, {\textsf{q}}(s) \, \big | \, {\textsf{t}}(s)=t \,\right\} \end{aligned}$$(6.21)is a (true) \(\text {BV}\) solution that enjoys, moreover, the following property: for every \(t\in {\textrm{J}}[q]\) there exists an optimal jump transition
 such that
such that  for some \({{\hat{r}}} \in [0,1]\). Furthermore, there holds $$\begin{aligned} {\textrm{Var}}_{{\mathfrak {M}}_{0}^{\alpha }}(q;[t_0,t_1]) = \int _{{\textsf{s}}(t_0)}^{{\textsf{s}}(t_1)} {\mathfrak {M}}_{0}^{\alpha }[{\textsf{t}}, {\textsf{q}}, {\textsf{t}}', {\textsf{q}}'](s) \,\,\!{\textrm{d}}s \quad \text {for all}\; 0 \le t_0\le t_1\le T. \end{aligned}$$(6.22)
for some \({{\hat{r}}} \in [0,1]\). Furthermore, there holds $$\begin{aligned} {\textrm{Var}}_{{\mathfrak {M}}_{0}^{\alpha }}(q;[t_0,t_1]) = \int _{{\textsf{s}}(t_0)}^{{\textsf{s}}(t_1)} {\mathfrak {M}}_{0}^{\alpha }[{\textsf{t}}, {\textsf{q}}, {\textsf{t}}', {\textsf{q}}'](s) \,\,\!{\textrm{d}}s \quad \text {for all}\; 0 \le t_0\le t_1\le T. \end{aligned}$$(6.22) -
(2)
Conversely, assume additionally Hypothesis 6.13. Then, for every \(\text {BV}\) solution \(q:[0,T]\rightarrow {\textbf{Q}}\), there exists a non-degenerate, surjective \(\text {pBV}\) solution \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}}([0,{{{\textsf {S}}}}];[0,T]{\times }{\textbf{Q}})\) such that (6.21) and (6.22) hold.
-
(3)
If \(({\textsf{t}},{\textsf{q}}):[0,{{{\textsf {S}}}}]\rightarrow [0,T]{\times }{\textbf{Q}}\) is a (non-degenerate) enhanced \(\text {pBV}\) solution with \({\textsf{t}}(0)=0\) and \({\textsf{t}}({{{\textsf {S}}}})=T\), then every \(q:[0,T]\rightarrow {\textbf{Q}}\) given by (6.21) is an enhanced \(\text {BV}\) solution, and (6.22) holds.
-
(4)
Conversely, for any enhanced \(\text {BV}\) solution \(q:[0,T]\rightarrow {\textbf{Q}}\), there exists a (non-degenerate, surjective) enhanced \(\text {pBV}\) solution \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}}([0,{{{\textsf {S}}}}];[0,T]{\times }{\textbf{Q}})\) such that (6.21) and (6.22) hold.
Remark 6.16
(Greater generality of true \(\text {BV}\) solutions) Theorem 6.15 seems to suggest that true \(\text {BV}\) solutions are more general than their parametrized analogues. Indeed, while, under the standing assumptions of Sect. 4, parametrized solutions always give rise to true \(\text {BV}\) ones, the converse passage is possible under the additional Hypothesis 6.13. Hence, the set of true \(\text {BV}\) solutions is apparently bigger.
To emphasize this, we have chosen to prove that any limit curve q for a sequence \((q_{{\varepsilon _k}})_k\) of (non-parametrized) viscous solutions is a true \(\text {BV}\) solution, as stated in Theorem 6.8, by resorting to Theorem 5.12 for parametrized solutions. Namely, in Sect. 7.2 we will use that the graphs of a sequence \((q_{{\varepsilon _k}})_k\) of viscous solutions are contained in the image sets of their parametrized counterparts \(({\textsf{t}}_{{\varepsilon _k}}, {\textsf{q}}_{{\varepsilon _k}})_k\) and apply Theorem 5.12 to the latter curves, guaranteeing their convergence to a \(\text {pBV}\) solution \(({\textsf{t}},{\textsf{q}})\). We will then proceed to showing that q and \(({\textsf{t}},{\textsf{q}})\) are related by (6.21) and thus conclude, by Theorem 6.15(1), that q is a true \(\text {BV}\) solution.
Proof
\(\underline{\textit{Step 1: From }\text {pBV}\textit{ to }\text {BV}\textit{ solutions.}}\) First, we show that, given a \(\text {pBV}\) solution \(({\textsf{t}},{\textsf{q}}) = ({\textsf{t}},{\textsf{u}},{\textsf{z}})\), formula (6.21) defines a curve \(q=(u,z) \in \textrm{BV}([0,T];{\textbf{U}}) {\times }({\textrm{R}}_{\textrm{w}}([0,T];{\textbf{Z}}){\cap } \textrm{BV}([0,T];{\textbf{Z}}_{{\textrm{ri}}}))\). Indeed, let \({\textsf{s}}:[0,T]\rightarrow [0,\mathsf {{{{\textsf {S}}}}}] \) be any inverse of \({\textsf{t}}\), with jump set \( {\textrm{J}}[{\textsf{s}}]\). It can be easily checked that, since \(({\textsf{t}},{\textsf{q}}) = ({\textsf{t}},{\textsf{u}},{\textsf{z}}) \) is non-degenerate,
If for \(t\in {\textrm{J}}[{\textsf{s}}]\) we have \(q(t) = {\textsf{q}}(s_*)\) for some \(s_*\in [{{\textsf{s}}}(t^-), {{\textsf{s}}}(t^+)]\), then defining \({\textsf{s}}(t): = s_*\) gives the identity
From this, we deduce \(u\in \textrm{BV}([0,T];{\textbf{U}})\) and \(z\in \textrm{BV}([0,T];{\textbf{Z}}_{{\textrm{ri}}})\). Moreover, since \(\sup _{t\in [0,T]} {\mathfrak {E}}(q(t))\le E\) for some \(E>0\) and the functional \({\mathfrak {E}}+ \Vert \cdot \Vert _{\textbf{U}}+ \Vert \cdot \Vert _{{\textbf{Z}}_{{\textrm{ri}}}} \) has sublevels bounded in \({\textbf{U}}_{{\textrm{e}}}{\times }{\textbf{Z}}_{{\textrm{e}}}\), we also have \(z\in {\textrm{R}}_{\textrm{w}}([0,T];{\textbf{Z}}_{{\textrm{e}}})\) thanks to (6.5).
From (6.23) we easily deduce that
Furthermore, we mimic the argument from the proof of [42, Prop. 4.7] and observe that for every \(t\in {\textrm{J}}[q]\) the curve \({\textsf{q}}= ({\textsf{u}},{\textsf{z}}): [{{\textsf{s}}}(t^-), {{\textsf{s}}}(t^+)] \rightarrow {\textbf{U}}{\times }{\textbf{Z}}\), reparametrized in such a way that it is defined on the interval [0, 1], is an admissible transition curve between \( {q}(t^-)\) and \({q}(t^+)\). Hence,
Combining this with (6.24) we conclude that
for all \([t_0,t_1]\subset [0,T]\). Ultimately, we infer that q fulfills the energy-dissipation estimate (6.11).
In order to show that q complies with the stationary equation (6.10a) and the local stability condition (6.10b), we argue in the following way. Recalling the definition of the sets \(\mathsf {{\mathscr {G}}}^\alpha \) from (5.20), we introduce
Observe that the set \( {\mathscr {H}}^\alpha [q]\) is dense in [0, T]. Indeed, its complement \([0,T]{{\setminus }} {\mathscr {H}}^\alpha [q] = {\textsf{t}}({\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}])\) has null Lebesgue measure, since \({\textsf{t}}\) is constant on each connected component of the open set \({\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\). Therefore, by the lower semicontinuity properties of \({\mathscr {S}}_{\textsf{u}}^*\) and \({\mathscr {S}}_{\textsf{z}}^*\) ensured by Hypothesis 4.10, in the case \(\alpha \ge 1\) we immediately conclude (6.10a) and (6.10b). For \(\alpha \in (0,1)\), the above argument only yields (6.10b), and for the validity of (6.10a), we observe that for any \(t\notin {\textrm{J}}[q] \), then
Then, since \({\mathscr {S}}_{\textsf{u}}^*({\textsf{t}},{\textsf{q}}) \equiv 0\) on the set \(\{ s \in (0,{{{\textsf {S}}}}): {\textsf{t}}'(s) >0 \} \) as prescribed by Definition 5.6, we conclude that \({\mathscr {S}}_{\textsf{u}}^*(t,q(t))=0\).
Since q complies with (6.10a), (6.10b), and (6.11), by Proposition 6.6 we conclude that it is a true \(\text {BV}\) solution. In order to conclude (6.22), we observe that, for all \(0\le t_0\le t_1\le T\) and \( s_0\le s_1 \in [0,{{{\textsf{S}}}}]\) such that \({\textsf{t}}(s_i) = t_i\) for \(i\in \{0,1\}\), there holds
It is immediate to see that the above arguments also yield an enhanced \(\text {BV}\) solution from any enhanced \(\text {pBV}\) solution. Hence, assertions (1) and (3) are proved.
\(\underline{\textit{Step 2: From }\text {BV}\textit{ to }\text {pBV}\textit{ solutions.}}\) First of all, we show that, under the additional Hypothesis 6.13, with any true \(\text {BV}\) solution \(q\in \textrm{BV}([0,T];{\textbf{U}}) {\times }\textrm{BV}([0,T];{\textbf{Z}}_{{\textrm{ri}}})\) we can associate a curve \(({\textsf{t}},{\textsf{q}}) = ({\textsf{t}},{\textsf{u}},{\textsf{z}}) \in {\mathscr {A}}([0,{{{\textsf {S}}}}];[0, T]{\times }{\textbf{Q}})\) which is non-degenerate, surjective, satisfies (6.12) and
Indeed, along the lines of [42, Prop. 4.7] we introduce the parametrization \({\textsf{s}}\), defined on [0, T] by

We set \(I:= \cup _{m\in M} I_m\) with \(I_m = ({\textsf{s}}(t_{m}^-), {\textsf{s}}(t_{m}^+) )\). Hence, we define \(({\textsf{t}},{\textsf{q}}) = ({\textsf{t}},{\textsf{u}},{\textsf{z}})\) on \([0,{{{\textsf{S}}}}]{\setminus } I\) by \( {\textsf{t}}: = {\textsf{s}}^{-1}: [0,{{{\textsf{S}}}}]{{\setminus }} I \rightarrow [0,T] \) and \( {\textsf{q}}: = q {\circ } {\textsf{t}}\). In order to extend \({\textsf{t}}\) and \({\textsf{q}}\) to I, we need to use the fact that, by Hypothesis 6.13, for every \(m \in M\) there exists an optimal jump transition jump transition  , defined on the canonical interval [0, 1] and such that
, defined on the canonical interval [0, 1] and such that  for some \({{\hat{r}}}_m \in [0,1]\). We may then define \({\textsf{t}}\) and \({\textsf{q}}\) on \(I = \cup _{m\in M} I_m\) by
for some \({{\hat{r}}}_m \in [0,1]\). We may then define \({\textsf{t}}\) and \({\textsf{q}}\) on \(I = \cup _{m\in M} I_m\) by

It can be easily checked that \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}}([0,{{{\textsf {S}}}}]; [0,T]{\times }{\textbf{Q}})\). By construction, the curves q and \(({\textsf{t}},{\textsf{q}})\) satisfy (6.21). Furthermore, recalling (6.24) and the fact that  , it is not difficult to check that (6.27) holds. Therefore, since q is a \(\text {BV}\) solution, we infer that \(({\textsf{t}},{\textsf{q}}) \) is a \(\text {pBV}\) solution, and we obtain (6.22) by repeating the argument in (6.26).
, it is not difficult to check that (6.27) holds. Therefore, since q is a \(\text {BV}\) solution, we infer that \(({\textsf{t}},{\textsf{q}}) \) is a \(\text {pBV}\) solution, and we obtain (6.22) by repeating the argument in (6.26).
This argument also allows us to prove that any enhanced \(\text {BV}\) solution gives rise to an enhanced \(\text {pBV}\) solution. Hence, the proof of Theorem 6.15 is finished. \(\square \)
7 Proof of Our Major Results
This section focuses on the proofs of our main existence results for \(\text {pBV}\) and true \(\text {BV}\) solutions, i.e. Theorems 5.12 and 6.8. They will be carried out in Sects. 7.1 and 7.2, respectively. Moreover, Sect. 7.3 provides the proof of Proposition 5.19.
Throughout this section and, in particular, in the statement of the various auxiliary results, we will always tacitly assume the validity of Hypotheses 4.1, 4.2, 4.3, 4.5, 4.10, and of the parametrized chain rule from Hypotheses 5.8: recall that, by Lemma A.2 it implies the \(\text {BV}\)-chain rule (6.4).
7.1 Proof of Theorem 5.12
Our first result lays the ground for the vanishing-viscosity analysis of Theorem 5.12 by settling the compactness properties of a sequence of parametrized curves enjoying the a priori estimates (5.29). We have chosen to extrapolate such properties from the proof of Theorem 5.12, since we believe them to be of independent interest.
Prior to stating Proposition 7.1, let us specify the meaning of the third convergence in (7.2b) below. Indeed, the sequence \(({\textsf{u}}_k)_k\) is contained in a closed ball \({\overline{B}}_R \subset {\textbf{U}}\) by virtue of estimate (7.1) (cf. Hypothesis 4.7). Now, since \({\textbf{U}}\) is reflexive and separable, it is possible to introduce a distance \(d_{{\textrm{weak}}}\) inducing the weak topology on \({\overline{B}}_R\). Hence, convergence in \({\textrm{C}}^0 ([0,{{{\textsf{S}}}}]; {\textbf{U}}_{{\textrm{weak}}})\) means convergence in \({\textrm{C}}^0 ([0,{{{\textsf{S}}}}]; ({\textbf{U}}, d_{{\textrm{weak}}}))\).
Proposition 7.1
Let \(({\textsf{t}}_k, {\textsf{q}}_k)_k \subset {\textrm{AC}}([ 0,{{{\textsf{S}}}}]; [0,T]{\times }{\textbf{Q}})\), with \({\textsf{t}}_k\) non-decreasing and \({\textsf{q}}_k = ({\textsf{u}}_k, {\textsf{z}}_k)\), enjoy the following bounds, along a null sequence \((\varepsilon _k)_k\):
Then, there exist an admissible parametrized curve \(({\textsf{t}}, {\textsf{q}}) \in {\mathscr {A}} ([0,{{{\textsf{S}}}}]; [0,T]{\times }{\textbf{Q}})\) with \(\mathsf {q=(u,z)}\),
and a (not relabeled) subsequence such that the following convergences hold as \(k\rightarrow \infty \):
Proof
We split the proof in three steps.
\(\underline{\textit{Step 1. Compactness:}}\) From (7.1) we infer the following compactness information.
-
(1.A)
By the Ascoli–Arzelà Theorem, there exists a non-decreasing \({\textsf{t}}\in W^{1,\infty }(0,{{{\textsf {S}}}})\) such that \({\textsf{t}}_k\rightarrow {\textsf{t}}\) uniformly in \([0,{{{\textsf {S}}}}]\) and weakly\(^*\) in \( W^{1,\infty }(0,{{{\textsf {S}}}})\).
-
(1.B)
Since the sequence \(({\textsf{u}}_k)_k\) is bounded in \(W^{1,\infty }(0,{{{\textsf {S}}}};{\textbf{U}})\) we conclude that there exists \( {\textsf{u}}\) with the regularity from (7.2a) such that, along a not relabeled subsequence, the second convergence in (7.2b) holds for \(({\textsf{u}}_k)_k\). The convergence in \({\textrm{C}}^0([0,{{{\textsf{S}}}}];{\textbf{U}}_{{\textrm{weak}}})\) follows from an Ascoli–Arzelà type theorem, see e.g. [3, Prop. 3.3.1]).
-
(1.C)
From \(\sup _{s\in [0,{{{\textsf {S}}}}]} {\mathfrak {E}}({\textsf{q}}_k(s)) \le C\) we deduce that there exists a ball
$$\begin{aligned} {\overline{B}}_M^{{\textbf{Z}}_{{\textrm{e}}}}\subset {\textbf{Z}}_{{\textrm{e}}}\Subset {\textbf{Z}}\text { such that }{\textsf{z}}_k(s) \in {\overline{B}}_M^{{\textbf{Z}}_{{\textrm{e}}}}\;\text {for all}\;s\in [0,{{{\textsf {S}}}}]\;\text {and }\;k\in {\mathbb {N}}. \end{aligned}$$(7.3a)Using \({\textbf{Z}}_{{\textrm{e}}}\Subset {\textbf{Z}}\subset {\textbf{Z}}_{{\textrm{ri}}}\) and the coercivity (4.3b) of \({{\mathcal {R}}}\), Ehrling’s lemma gives that
$$\begin{aligned} \forall \, \omega>0 \ \exists \, C_\omega >0 \ \forall \, z\in {\overline{B}}_M^{{\textbf{Z}}_{{\textrm{e}}}}: \quad \Vert z\Vert _{{\textbf{Z}}} \le \omega +C_\omega {{\mathcal {R}}}(z). \end{aligned}$$Hence, defining \(\Omega _M(r): = \inf _{\omega >0} ( \omega {+}C_\omega r)\) and noting that \(\Omega _M(\lambda r) \le \lambda \Omega _M(r)\) for all \(\lambda \ge 1\), we find
$$\begin{aligned} \Vert {\textsf{z}}_k(s_1) {-} {\textsf{z}}_k(s_2) \Vert _{{\textbf{Z}}}\le & {} \Omega _M({{\mathcal {R}}}({\textsf{z}}_k(s_1) {-} {\textsf{z}}_k(s_2) )) \nonumber \\\le & {} C_* \Omega _M(|s_1{-}s_2|)\;\text {for all}\; 0 \le s_1\le s_2 \le {{{\textsf {S}}}}, \end{aligned}$$(7.3b)where the last estimate follows from the bound for \({{\mathcal {R}}}({\textsf{z}}'_k)\) in (7.1). We combine the compactness information provided by (7.3a) with the equicontinuity estimate (7.3b) and again apply, [3, Prop. 3.3.1] to deduce that there exists \({\textsf{z}}\in {\textrm{C}}^0([0,{{{\textsf {S}}}}];{\textbf{Z}})\) such that, along a not relabeled subsequence, \(({\textsf{z}}_k)_k\) converges to \({\textsf{z}}\) in the sense of (7.2b).
Let us denote by \({\textsf{q}}\) the curve \( ({\textsf{u}}, {\textsf{z}})\).
\(\underline{\textit{Step 2. }{\textsf{q}}\textit{ is an admissible parametrized curve:}}\) Combining the previously found convergences with the first estimate in (7.1), we obtain \( \sup _{s\in [0,{{{\textsf {S}}}}]} {\mathfrak {E}}({\textsf{q}}(s)) \le C\). Using the second estimate in (7.1) and (4.3b) we have \(\Vert {\textsf{z}}(s_2){-}{\textsf{z}}(s_1)\Vert _{{\textbf{Z}}_{{\textrm{ri}}}} \le C_*|s_2{-}s_1|/c_{{\mathcal {R}}}\). With (7.3b) we also infer that \({\textsf{z}}\in {\textrm{C}}_{{\textrm{lip}}}^0([0,{{{\textsf{S}}}}]; {\textbf{Z}}_{{\textrm{ri}}})\).
We will now show that \({\textsf{z}}\) is locally absolutely continuous in the set \( {\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\) from (5.20). Let us first examine the case \(\alpha \in (0,1)\). Since the function \(s\mapsto {\mathscr {S}}_{\textsf{z}}^*({\textsf{t}}(s),{\textsf{q}}(s))\) is lower semicontinuous thanks to Hypothesis 4.10, for every \([\varsigma ,\beta ] \subset {\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}] \) there exists \( c>0\) such that \({\mathscr {S}}_{\textsf{z}}^*({\textsf{t}}(s),{\textsf{q}}(s)) \ge c\) for all \(s\in [\varsigma ,\beta ]\). This estimate bears two consequences:
-
(1)
Exploiting the uniform convergence of \({\textsf{z}}_k\) to \({\textsf{z}}\) and again relying on Hypothesis 4.10,
$$\begin{aligned} \exists \, {{\bar{k}}} \in {\mathbb {N}}\ \forall \, k \ge {{\bar{k}}} \, \ \forall \, s \in [\varsigma ,\beta ]: ~{\mathscr {S}}_{\textsf{z}}^*({\textsf{t}}_k(s),{\textsf{q}}_k(s)) \ge \frac{c}{2}. \end{aligned}$$(7.4)This implies that, for \(k\ge {{\bar{k}}}\), the sets \( {\mathscr {G}}^{\alpha }[{\textsf{t}}_k,{\textsf{q}}_k] = \{ s: {\mathscr {S}}_{\textsf{z}}^*({\textsf{t}}_k(s),{\textsf{q}}_k(s))>0 \} \) contain the interval \([\varsigma ,\beta ]\).
-
(2)
Since, by (7.1), \(C_* \ge {\mathfrak {M}}_{{\varepsilon _k}}^{\alpha ,{\textrm{red}}}({\textsf{t}}_k(s),{\textsf{q}}_k(s), {\textsf{t}}_k'(s),{\textsf{q}}_k'(s)) \) for almost all \(s\in (\varsigma ,\beta )\), we are in a position to apply estimate (5.15a) from Lemma 5.4 and deduce that
$$\begin{aligned} \exists \, {{\overline{C}}}>0 \ \exists \, {{\bar{k}}} \in {\mathbb {N}}\ \forall \, k \ge {{\bar{k}}} \ \text {for a.a. }s \in (\varsigma ,\beta ):~ \Vert {\textsf{z}}_k'(s)\Vert _{{\textbf{Z}}} \le {\overline{C}}. \end{aligned}$$(7.5)
The discussion of the case \(\alpha \ge 1\) follows the very same lines: for every \([\varsigma ,\beta ] \subset {\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\) we find \({\tilde{c}}>0\) and \({{\tilde{k}}} \in {\mathbb {N}}\) such that for every \(k \ge {{\tilde{k}}}\) we have \( {\mathscr {S}}_{\textsf{u}}^*({\textsf{t}}_k(s),{\textsf{q}}_k(s)) {+} {\mathscr {S}}_{\textsf{z}}^*({\textsf{t}}_k(s),{\textsf{q}}_k(s)) \ge \frac{{\tilde{c}}}{2}\) for every \(s\in [\varsigma ,\beta ]\). Then, estimate (7.5) follows from (5.15b) in Lemma 5.4.
All in all, for all \(\alpha >0\) the curves \({\textsf{z}}_k\) are uniformly \({\textbf{Z}}\)-Lipschitz on \([\varsigma ,\beta ]\). This entails that \({\textsf{z}}\) is ultimately \({\textbf{Z}}\)-Lipschitz on any subinterval \([s_1,s_2] \subset {\mathscr {G}}^{\alpha }[{\textsf{t}},{\textsf{q}}]\), and reflexivity of \({\textbf{Z}}\) gives us
\(\underline{\textit{Step 3. Proof of (7.2c):}}\) In order to conclude that \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}} ([0,{{{\textsf{S}}}}]; [0,T]{\times }{\textbf{Q}})\), it remains to show that it fulfills property (5.21), which will be a consequence of (7.2c). By the lower semicontinuity we have
with \( \overset{(1)}{=}\ \) and \(\overset{(2)}{=}\ \) due to (6.3). Furthermore, we have
Here, \( \overset{(3)}{\ge }\ \) follows from Proposition 5.13, applied to the functionals \( {\mathfrak {M}}_{{\varepsilon _k}}^{\alpha ,{\textrm{red}}}\) and \({\mathfrak {M}}_{0}^{\alpha ,{\textrm{red}}}\), which we consider restricted to the (weakly closed, by assumption (4.7a)) energy sublevel \({\textbf{S}}= \{ q \in {\textbf{Q}}: {\mathfrak {E}}(q) \le C\}\). Combining (7.7) and (7.8), we infer (7.2c) and thus conclude the proof of Proposition 7.1. \(\square \)
We are now in the position to conclude the
Proof of Theorem 5.12
Let \(({\textsf{t}}_{\varepsilon _k},{\textsf{q}}_{\varepsilon _k})_k \) be a sequence of rescaled viscous trajectories satisfying (5.29). We apply Proposition 7.1 and conclude that there exist a limit parametrized curve \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}}([0,{{{\textsf{S}}}}];[0,T]{\times }{\textbf{Q}})\), fulfilling (5.30), and a (not relabeled) subsequence along which convergences (5.31) hold.
We now show that the curves \(({\textsf{t}},{\textsf{q}}) \) fulfill the upper energy-dissipation estimate \(\le \) in (5.25) by passing to the limit as \({\varepsilon _k}\rightarrow 0^+\) in (5.4) for \(s_1=0\) and \(s_2= s\in (0,{{{\textsf{S}}}}]\). The key lower semicontinuity estimate
follows from (7.2c) in Proposition 7.1. Convergences (5.31), the lower semicontinuity (4.7b) of \({{\mathcal {E}}}\), and the continuity (4.14) of \(\partial _t {{\mathcal {E}}}\) give for all \(s\in [0,{{{\textsf{S}}}}]\) that
For the last convergence we use \({\textsf{t}}'_k \overset{*}{\rightharpoonup }{\textsf{t}}'\) in \({\textrm{L}}^\infty (0,{{{\textsf{S}}}})\) and \(|\partial _t {\mathcal {E}}({\textsf{t}}_{\varepsilon _k}(\sigma ),{\textsf{q}}_{\varepsilon _k}(\sigma )) | \le C_\# {\mathcal {E}}({\textsf{t}}_{\varepsilon _k}(\sigma ),{\textsf{q}}_{\varepsilon _k}(\sigma )) \le C\) by (4.7d) and (4.26), which together with (4.14) gives \(\partial _t {\mathcal {E}}({\textsf{t}}_{\varepsilon _k},{\textsf{q}}_{\varepsilon _k}) \rightarrow \partial _t {\mathcal {E}}({\textsf{t}},{\textsf{q}}) \) strongly in \({\textrm{L}}^2(0,{{{\textsf{S}}}})\).
Taking into account the convergence of the initial energies guaranteed by (5.28), we complete the limit passage in (5.4). Thanks to Lemma 5.11, the validity of the upper energy-dissipation estimate in (5.25) ensures that \(({\textsf{t}},{\textsf{q}}) = ({\textsf{t}},{\textsf{u}},{\textsf{z}})\) is a \(\text {pBV}\) solution.
The enhanced convergences (5.32a) and (5.32b) are a by-product of this limiting procedure. Although the argument is standard, we recap it for the reader’s convenience and later use, and introduce the following place-holders for every \(s\in [0,{{{\textsf{S}}}}]\):
Hence, the parametrized energy-dissipation estimate (5.4) rephrases as \( E_{{\varepsilon _k}}^s +M^s_{\varepsilon _k}\le E_{{\varepsilon _k}}^0+ P^s_{\varepsilon _k}\), and the limiting energy-dissipation balance rewrites as \( E_{0}^s +M_0 = E_{0}^0 + P^s_0 \). So far, we have shown that
Since we have \(\liminf _{k\rightarrow \infty } E_{{\varepsilon _k}}^s \ge E_0^s\) and \(\liminf _{k\rightarrow \infty } M^s_{\varepsilon _k}\ge M^s_0\), we thus conclude that \(\liminf _{k\rightarrow \infty } E_{{\varepsilon _k}}^s = E_0^s\) and \(\lim _{k\rightarrow \infty }M^s_{\varepsilon _k}= M^s_0\) for all \(s\in [0,{{{\textsf{S}}}}]\), which means (5.32). Thus, Theorem 5.12 is established. \(\square \)
7.2 Proof of Theorem 6.8
Proof
We split the argument in three steps.
\(\underline{\textit{Step 1. Construction of a suitable }\text {pBV}\textit{ solution.}}\) Let \((q_{{\varepsilon _k}})_k\), q be as in the statement of Theorem 6.8. Lemma 4.12 ensures the validity of the basic energy estimates (4.25) and (4.26) for the sequence \((q_k)_k = (u_{{\varepsilon _k}},z_{\varepsilon _k})_k\). The additional estimate for \((u_{\varepsilon _k})_k\) in \(\textrm{BV}([0,T];{\textbf{U}}) \) is assumed in (6.15), such that the arc-length functions \({\textsf{s}}_{{\varepsilon _k}}\) from (5.2) fulfill \(\sup _{k\in {\mathbb {N}}} {\textsf{s}}_{\varepsilon _k}(T) \le C\). We reparametrize the curves \(q_{\varepsilon _k}\) by means of the rescaling functions \({\textsf{t}}_{\varepsilon _k}: = {\textsf{s}}_{\varepsilon _k}^{-1}\) by setting \({\textsf{q}}_{\varepsilon _k}: = q_{\varepsilon _k}{\circ } {\textsf{t}}_{\varepsilon _k}\). Without loss of generality we may suppose that \(({\textsf{t}}_{\varepsilon _k},{\textsf{q}}_{\varepsilon _k})\) is surjective and defined on a fixed interval \([0,{{{\textsf{S}}}}]\).
Now, for the sequence \(({\textsf{t}}_{\varepsilon _k}, {\textsf{q}}_{\varepsilon _k})_k\) the a priori estimate (5.29) holds. Hence, we are in a position to apply Theorem 5.12 to the curves \(({\textsf{t}}_{\varepsilon _k},{\textsf{q}}_{\varepsilon _k})_k\) and we conclude that \(({\textsf{t}}_{\varepsilon _k},{\textsf{q}}_{\varepsilon _k})_k\) convergence along a (not relabeled) subsequence to a \(\text {pBV}\) solution \(({\textsf{t}},{\textsf{q}}): [0,{{{\textsf{S}}}}]\rightarrow [0,T]{\times }{\textbf{Q}}\). In what follows, we will prove that q is related to the parametrized curve \(({\textsf{t}},{\textsf{q}})\) via (6.21).
\(\underline{\textit{Step 2. Every limit point }q\textit{ is a true }\text {BV}\textit{ solution:}}\) We first prove that
For this we fix \(t_*\in [0,T]\) and choose \(s_k\in [0,{{{\textsf{S}}}}]\) such that \({\textsf{t}}_{\varepsilon _k}(s_k)=t_*\). After choosing a (not relabeled) subsequence we may assume \(s_k\rightarrow s_*\). As \(({\textsf{t}}_{\varepsilon _k},{\textsf{q}}_{\varepsilon _k})_k\) converges uniformly to \(({\textsf{t}},{\textsf{q}})\) in \({\textrm{C}}^0([0,{{{\textsf{S}}}}];{\mathbb {R}}{\times }{\textbf{Q}}_{\textrm{weak}})\) we obtain
However, by construction we have
where the last convergence is the assumption in (6.16). Hence we conclude \({\textsf{t}}(s_*)=t_*\) and \({\textsf{q}}(s_*)=q(t_*)\) which is the desired relation (7.11).
Thanks to (7.11), we can apply Theorem 6.15(1), which ensures that q is a true \(\text {BV}\) solution.
\(\underline{\textit{Step 3. Proof of convergences (6.17):}}\) Since \((q_{\varepsilon _k})_k\) is bounded in \({\textrm{L}}^\infty (0,T;{\textbf{U}}_{{\textrm{e}}}{\times }{\textbf{Z}}_{{\textrm{e}}})\) by estimate (4.26) and Hypothesis 4.3, the pointwise weak convergence in \({\textbf{Q}}\) improves to convergences (6.17a). Next, we observe that for every \( 0 \le s_0 \le s_1 \le {{{\textsf {S}}}}\) there holds
with (1) due to (5.32b) and (2) due to (6.22). Hence, (6.17c) follows.
Finally, the lower semicontinuity of \({{\mathcal {E}}}\), the continuity (4.14) of \(\partial _t {{\mathcal {E}}}\), give that
Hence, with similar arguments as in the proof of Theorem 5.12 (cf. the end of Sect. 7.1), we conclude, for all \(t \in [0, T]\), the identity
and (6.17b) ensues from the previously obtained (6.17c). This finishes the proof of Theorem 6.8. \(\square \)
7.3 Proof of Proposition 5.19
Our task is to show inclusions (5.46) for the contact sets \(\Sigma _\alpha \) and the flow regimes \({\textrm{A}}_{\textsf{u}} {\textrm{C}}_{\textsf{z}}\) for the three different cases for \(\alpha \). We rely on the explicit form of \({\mathfrak {M}}_{0}^{\alpha }={{\mathcal {R}}}+{\mathfrak {M}}_{0}^{\alpha ,{\textrm{red}}}\) from (5.12).
Proof of Proposition 5.19
\(\underline{\textit{Step 1: The case }t'>0.}\) We start by showing that for all \(\alpha >0\) we have
Indeed, in the case \(t'>0\) we have \({\mathfrak {M}}_{0}^{\alpha }(t,q,t',q') <\infty \) if and only if \({\mathscr {S}}_{\textsf{u}}^*(t,q) ={\mathscr {S}}_{\textsf{z}}^*(t,q) =0\) and then \({\mathfrak {M}}_{0}^{\alpha }(t,q,t',q') = {{\mathcal {R}}}(z')\). From the former we obtain that, in fact, every \((\mu ,\zeta )\in {\mathfrak {A}}_{\textsf{u}}^{*}(t,q) {\times } {\mathfrak {A}}_{\textsf{z}}^{*}(t,q)\) satisfies \(\mu =0\) and \(-\zeta \in \partial {{\mathcal {R}}}(0)\). From the contact condition  and the 1-homogeneity of \({{\mathcal {R}}}\) we infer that \(-\zeta \in \partial {{\mathcal {R}}}(z')\), see (4.5). Taking into account that \({\mathfrak {A}}_{\textsf{x}}^{*}(t,q) \subset \partial _{\textsf{x}}{{\mathcal {E}}}(t,q)\) for \({\textsf{x}} \in \{{\textsf{u}}, {\textsf{z}}\}\), we ultimately infer
and the 1-homogeneity of \({{\mathcal {R}}}\) we infer that \(-\zeta \in \partial {{\mathcal {R}}}(z')\), see (4.5). Taking into account that \({\mathfrak {A}}_{\textsf{x}}^{*}(t,q) \subset \partial _{\textsf{x}}{{\mathcal {E}}}(t,q)\) for \({\textsf{x}} \in \{{\textsf{u}}, {\textsf{z}}\}\), we ultimately infer
namely system (5.44) holds with \(\lambda _{\textsf{u}} = \lambda _{\textsf{z}} =0\), i.e. \((t,q,t',q') \in {\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}} \). Hence, we have shown \(\Sigma _\alpha ^{>0} \subset {\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}}\). In fact, reverting the arguments the opposite inclusion holds as well.
\(\underline{\textit{Step 2. The case }t'=0.}\) We define \(\Sigma _\alpha ^0:= \left\{ \, (t,q,t',q')\in \Sigma _{\alpha }\, \big | \, t'=0 \,\right\} \) and treat the three cases \(\alpha =1\), \(\alpha >1\), and \(\alpha \in (0,1)\), separately.
\(\underline{\textit{Step 2.A. }t'=0\textit{ and }\alpha =1.}\) We want to show the inclusion
From (5.12) we have \({\mathfrak {M}}_{0}^{\alpha }(t,q,0,q')={{\mathcal {R}}}(z')+{\mathfrak {b}}_{{{\mathcal {V}}}_{\textsf{u}} \oplus {{\mathcal {V}}}_{\textsf{z}}}(q',{\mathscr {S}}_{\textsf{u}}^*(t,q){+}{\mathscr {S}}_{\textsf{z}}^*(t,q))\). Hence, for \({\mathscr {S}}_{\textsf{u}}^*(t,q){+}{\mathscr {S}}_{\textsf{z}}^*(t,q)=0\) we argue as in Step 1 and obtain \((t,q,0,q')\in {\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}} \cap \{t'=0\}\).
We may now suppose that \({\mathscr {S}}_{\textsf{u}}^*(t,q) {+} {\mathscr {S}}_{\textsf{z}}^*(t,q)>0\) and \(q'=(u',z')=0\). Clearly, the contact condition  holds for all \((\mu ,\zeta ) \in {\mathfrak {A}}_{\textsf{u}}^{*}(t,q) {\times } {\mathfrak {A}}_{\textsf{z}}^{*}(t,q)\). However, \({\mathscr {S}}_{\textsf{u}}^*(t,q) {+} {\mathscr {S}}_{\textsf{z}}^*(t,q)>0\) gives \(\big (\{0\}{\times }\partial {{\mathcal {R}}}(0) \big )\cap \partial _{\textsf{q}}{{\mathcal {E}}}(t,q) = \varnothing \), and because of \( {\mathfrak {A}}_{\textsf{u}}^{*}(t,q) {\times } {\mathfrak {A}}_{\textsf{z}}^{*}(t,q) \subset \partial _{\textsf{q}}{{\mathcal {E}}}(t,q)\) we conclude that (t, q, 0, (0, 0)) fulfills system (5.44) with \(\lambda _{\textsf{u}} = \lambda _{\textsf{z}} =\infty \). Hence, \((t,q,0,q')=(t,q,0,0) \in {\textrm{B}}_{\textsf{u}} {\textrm{B}}_{\textsf{z}}\) as desired.
holds for all \((\mu ,\zeta ) \in {\mathfrak {A}}_{\textsf{u}}^{*}(t,q) {\times } {\mathfrak {A}}_{\textsf{z}}^{*}(t,q)\). However, \({\mathscr {S}}_{\textsf{u}}^*(t,q) {+} {\mathscr {S}}_{\textsf{z}}^*(t,q)>0\) gives \(\big (\{0\}{\times }\partial {{\mathcal {R}}}(0) \big )\cap \partial _{\textsf{q}}{{\mathcal {E}}}(t,q) = \varnothing \), and because of \( {\mathfrak {A}}_{\textsf{u}}^{*}(t,q) {\times } {\mathfrak {A}}_{\textsf{z}}^{*}(t,q) \subset \partial _{\textsf{q}}{{\mathcal {E}}}(t,q)\) we conclude that (t, q, 0, (0, 0)) fulfills system (5.44) with \(\lambda _{\textsf{u}} = \lambda _{\textsf{z}} =\infty \). Hence, \((t,q,0,q')=(t,q,0,0) \in {\textrm{B}}_{\textsf{u}} {\textrm{B}}_{\textsf{z}}\) as desired.
Suppose now \( {{\mathcal {V}}}_{\textsf{z}} (z') {+} {{\mathcal {V}}}_{\textsf{u}} (u')>0\) in addition to \({\mathscr {S}}_{\textsf{u}}^*(t,q) {+} {\mathscr {S}}_{\textsf{z}}^*(t,q)>0\). According to Proposition 3.2(b2) there exists \(\ell = \ell (t,q,q')>0\) with
Now, \((t,q,0,q') \in \Sigma ^0_1\) means that there exists \((\mu ,\zeta ) \in {\mathfrak {A}}_{\textsf{u}}^{*}(t,q) {\times } {\mathfrak {A}}_{\textsf{z}}^{*}(t,q)\) fulfilling the contact condition

Moreover, the definition of \({\mathfrak {A}}_{\textsf{x}}^{*}(t,q)\) gives \({\mathscr {S}}_{\textsf{u}}^*(t,q)={{\mathcal {V}}}_{\textsf{u}}^*({-}\mu )\) and \({\mathscr {S}}_{\textsf{z}}^*(t,q)={\mathcal {W}}_{\textsf{z}}^*({-}\zeta )\). Together with the definition of \(\ell \) we find the identity

Since \({{\mathcal {V}}}_{\textsf{u}}^*\oplus {\mathcal {W}}_{\textsf{z}}^*\) is is the Legendre–Fenchel dual of \({{\mathcal {V}}}_{\textsf{u}} \oplus ({{\mathcal {R}}}{+}{{\mathcal {V}}}_{\textsf{z}})\) we conclude
From this we see that \((t,q,0,q')\) system (5.44) holds with \(\lambda _{\textsf{u}} = \lambda _{\textsf{z}} = 1/\ell \in (0,\infty )\), i.e. we have \((t,q,0,q') \in {\textrm{V}}_{\textsf{uz}}\), and the inclusion (7.13) is established.
\(\underline{\textit{Step 2.B. }t'=0\textit{ and }\alpha >1.}\) Let us now examine the case \(\alpha >1\) and prove that
Using the explicit expression for \({\mathfrak {M}}_{0}^{\alpha ,{\textrm{red}}}(t,q, 0,q')\) in (5.12), we see that \({\mathfrak {M}}_{0}^{\alpha }(t,q, 0,q') < \infty \) implies that either (i) \({\mathscr {S}}_{\textsf{u}}^*(t,q)=0\) or (ii) \(\big ({\mathscr {S}}_{\textsf{u}}^*(t,q)>0\) and \(z'=0\big )\).
In case (i), which means \({\textrm{E}}_{\textsf{u}}\), the contact condition reads

If \({\mathscr {S}}_{\textsf{z}}^*(t,q)=0\), we have \({\mathfrak {b}}_{\psi _{\textsf{z}}}(z', {\mathscr {S}}_{\textsf{z}}^*(t,q))=0\) and infer  . Moreover, \({\mathscr {S}}_{\textsf{z}}^*(t,q)=0\) implies \(\zeta \in {\mathfrak {A}}_{\textsf{z}}^{*}(t,q)=\partial {{\mathcal {R}}}(0)\), and we conclude \(\partial {{\mathcal {R}}}(z') + \zeta \ni 0\) by (4.5). Hence, we can choose \(\lambda _{\textsf{z}}=0\) in (5.44b) and obtain \((t,q,0,q')\in {\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}}\).
. Moreover, \({\mathscr {S}}_{\textsf{z}}^*(t,q)=0\) implies \(\zeta \in {\mathfrak {A}}_{\textsf{z}}^{*}(t,q)=\partial {{\mathcal {R}}}(0)\), and we conclude \(\partial {{\mathcal {R}}}(z') + \zeta \ni 0\) by (4.5). Hence, we can choose \(\lambda _{\textsf{z}}=0\) in (5.44b) and obtain \((t,q,0,q')\in {\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}}\).
If \(z'=0\) holds but not \({\mathscr {S}}_{\textsf{z}}^*(t,q)>0\), then (5.44b) holds for \(\lambda _{\textsf{z}}=\infty \) and \((t,q,0,q')\in {\textrm{B}}_{\textsf{z}}\).
Finally, if \(z'\ne 0\) and \({\mathscr {S}}_{\textsf{z}}^*(t,q)>0\), then the very same discussion as in the last part of Step 2.A provides \(\lambda _{\textsf{z}} \in (0,\infty )\) such that \( \partial {{\mathcal {R}}}(z') + \partial {{\mathcal {V}}}_{\textsf{z}}^{ \lambda _{\textsf{z}}} (z') + \partial _{\textsf{z}}{{\mathcal {E}}}(t,q) \ni 0 \), which means \((t,q,0,q')\in {\textrm{E}}_{\textsf{u}} {\textrm{V}}_{\textsf{z}}\).
The discussion of the case (ii) with \({\mathscr {S}}_{\textsf{u}}^*(t,q)>0\) and \(z'=0\) proceeds along the same lines, relying on the contact condition

For \(u' \ne 0\) we find \(\lambda _{\textsf{u}}\in (0,\infty )\) with \(\partial {{\mathcal {V}}}_{\textsf{u}}^{\lambda _{\textsf{u}}}(u') + \mu \ni 0\), which gives \((t,q,0,q')\in {\textrm{V}}_{\textsf{u}} {\textrm{B}}_{\textsf{z}}\). For \(u'=0\) we can choose \(\lambda _{\textsf{u}}=\infty \) such that \(\partial {{\mathcal {V}}}_{\textsf{u}}^{\infty }(0) + \mu ={\textbf{U}}^*+\mu \ni 0\). Hence (5.44) holds with \(\lambda _{\textsf{z}}=\infty \) and \(\lambda _{\textsf{u}}\in (0,\infty ]\), i.e. \((t,q,0,q')\in {\textrm{B}}_{\textsf{z}}\).
Thus, in both cases, (i) and (ii), we conclude (7.14), and Step 2.B is completed.
\(\underline{\textit{Step 2.C. }t'=0\textit{ and }\alpha \in (0,1).}\) This case works similarly as the case \(\alpha >1\) in Step 2.B, but with the roles of u and z interchanged, where \({\textrm{E}}_{\textsf{u}}\) is interchanged with \({\textrm{R}}_{\textsf{z}}\). Thus, in analogy to (7.13) we obtain \(\Sigma ^0_\alpha \subset \big ({\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}} \cap \{t'=0\}\big ) \cup {\textrm{V}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}} \cup {\textrm{B}}_{\textsf{u}} \).
This concludes the proof of Proposition 5.19. \(\square \)
8 Application to a Model for Delamination
In this section we discuss the application of our vanishing-viscosity analysis techniques to a PDE system modeling adhesive contact. A previous vanishing-viscosity (and vanishing-inertia, in the momentum balance) analysis was carried out for a delamination model in [58] where, however, an energy balance only featuring defect measures, in place of contributions describing the dissipation of energy at jumps, was obtained in the null-viscosity limit.
After introducing the viscous model and discussing its structure as a generalized gradient system in Sect. 8.1, we are going to state the existence of enhanced \(\text {BV}\) and parametrized solutions to the corresponding rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) in Theorem 8.1. This result will be proved throughout Sects. 8.2–8.5 by showing that the ‘abstract’ Theorems 5.15 and 6.12 apply.
As we will emphasize later on, our analysis crucially relies on the fact that, in the delamination system, the coupling between the displacements and the delamination parameter only occurs through lower order terms.
8.1 The ‘Viscous’ System for Delamination
We consider two bodies located in two bounded Lipschitz domains \(\Omega ^\pm \subset {\mathbb {R}}^3\) and adhering along a prescribed interface \(\Gamma _{{\textrm{C}}}\), on which some adhesive substance is present. We denote that part of \(\Omega ^\pm \) that coincides with \(\Gamma _{{\textrm{C}}}\) by \(\Gamma _\pm \), see Fig. 2, thus being able to talk about one-sided boundary conditions. In what follows, for simplicity we will assume that \(\Gamma _{{\textrm{C}}}\) is a ‘flat’ interface, i.e., \( \Gamma _{{\textrm{C}}}\) is contained in a plane, so that, in particular, \({\mathscr {H}}^{2}(\Gamma _{{\textrm{C}}}) ={\mathscr {L}}^{2}(\Gamma _{{\textrm{C}}}) >0\). While the generalization to a smooth curved interface is standard, this restriction will allow us to avoid resorting to Laplace–Beltrami operators in the flow rule for the delamination parameter.
The state variables in the model are indeed the displacement \(u: \Omega \rightarrow {\mathbb {R}}^3\), with \(\Omega : = \Omega ^+ \cup \Omega ^- \), and the delamination variable \(z: \Gamma _{{\textrm{C}}}\rightarrow [0,1]\), representing the fraction of fully effective molecular links in the bonding. Therefore, \(z(t,x) =1\) (\(z(t,x)=0\), respectively) means that the bonding is fully intact (completely broken) at a given time instant \(t\in [0,T]\) and in a given material point \(x\in \Gamma \). We denote by \(n^\pm \) the outer unit normal of \(\Omega ^\pm \) restricted to \(\Gamma _\pm \) and by \(\llbracket u \rrbracket \) the jump of u across \(\Gamma _{{\textrm{C}}}\), namely \(\llbracket u \rrbracket = u|_{\Gamma _+} - u|_{\Gamma _-}\), but now defined as function on \(\Gamma _{{\textrm{C}}}\).
For simplicity, we impose homogeneous Dirichlet boundary conditions \(u=0\) on the Dirichlet part \(\Gamma _{{\textrm{D}}}\) of the boundary \(\partial \Omega \), with \({\mathscr {H}}^2(\Gamma _{{\textrm{D}}})>0\). We consider a given applied traction f on the Neumann part \(\Gamma _{{\textrm{N}}}=\partial \Omega {{\setminus }} (\Gamma _{{\textrm{D}}}{\cup } \Gamma _{{\textrm{C}}}) \).
All in all, we address the following rate-dependent PDE system
where \(\dot{u}\) and \(\dot{z}\) stand for the partial time derivatives of u and z. Here, F is a volume force, \({\mathbb {D}},\, {\mathbb {C}}\in \text {Lin}({\mathbb {R}}^{d {\times }d}_{\textrm{sym}} ) \) the positive definite and symmetric viscosity and elasticity tensors, \(\nu \) the exterior unit normal to \(\partial (\Omega ^+ {\cup } \Gamma _{{\textrm{C}}}{\cup } \Omega ^-)\), and \({\textrm{R}}\) is given by
Hence, healing of the broken molecular links is disfavored, but not totally blocked. Giving up unidirectionality allows for a more straightforward application of our abstract results. Nonetheless, we expect that, at the price of some further technicalities our techniques could be adapted to deal with unidirectionality by means of additional estimates (like for instance in the application of \(\text {BV}\) solutions to unidirectional damage developed in [23]).
The term \(\gamma (z)\partial \psi (\llbracket u \rrbracket )\), with \(\gamma \) and \(\psi \) nonnegative functions (we may think of \(\gamma (z) = \max \{ z, 0\}\)) and \(\psi \) convex, in (8.1d) derives from the contribution \(\gamma (z) \psi (\llbracket u \rrbracket )\) to the surface energy, cf. (8.6d) ahead, which penalizes the constraint \(z\llbracket u \rrbracket =0\) a.e. on \(\Gamma _{{\textrm{C}}}\), typical of brittle delamination models. Indeed, to our knowledge, existence results for brittle models are available only in the case of a rate-independent evolution for z, cf. e.g. [49, 57]. In fact, (8.1) is rather a model for contact with adhesion and will be accordingly referred to in this way. Our assumptions on the constitutive functions \(\gamma \), \(\psi \) and \(\beta \), and on the multivalued operator \({{\tilde{\phi }}}\) (indeed, on the mapping \(z\mapsto {{\tilde{\phi }}}(z) -z\)), will be specified in (8.5) ahead.
We define the operators \({{\textbf { C}}},{{\textbf { D}}}: {\textrm{H}}^1(\Omega ;{\mathbb {R}}^3)\rightarrow {\textrm{H}}^1(\Omega ;{\mathbb {R}}^3)^*\) via

while we denote by \({\varvec{J}}:\mathrm {\textrm{H}}^1(\Omega ;{\mathbb {R}}^3)\rightarrow {\textrm{L}}^4(\Gamma _{{\textrm{C}}};{\mathbb {R}}^3); \; u\mapsto \llbracket u \rrbracket \) the jump operator, by \(\Vert {\varvec{J}}\Vert \) its operator norm, and by \({\varvec{J}}^*\) its adjoint. We denote by \({{\textbf { A}}}\) the Laplacian with homogeneous Neumann boundary conditions

In particular, we have  . Finally, we denote by \(\ell _u: (0,T)\rightarrow {\textbf{U}}^*\) the functional encompassing the volume and surface forces F and f, namely
. Finally, we denote by \(\ell _u: (0,T)\rightarrow {\textbf{U}}^*\) the functional encompassing the volume and surface forces F and f, namely

Throughout, we will assume that
Hence, system (8.1) takes the form
almost everywhere in (0, T). In (8.4), \({\widehat{\beta }}\) a primitive for \(\beta \) and \(\widehat{\phi }\) a primitive for the multivalued operator \(z \mapsto {{\tilde{\phi }}}(z)-z\).
8.1.1 Structure as a (Generalized) Gradient System
First of all, let us specify our assumptions on the constitutive functions \({{\widehat{\beta }}}\), \(\gamma \), \({{\widehat{\phi }}}\), and \(\psi \):
Hence, \(\partial \gamma \) and \(\partial \psi \) in (8.4) are convex analysis subdifferentials, while \(\partial \widehat{\phi }:{\mathbb {R}}\rightrightarrows {\mathbb {R}}\) is the Fréchet subdifferential of \(\widehat{\phi }\).
To fix ideas, prototypical choices for \({{\widehat{\beta }}}\), \(\gamma \), \({{\widehat{\phi }}}\), and \(\psi \) would be:
-
(i)
\({{\widehat{\beta }}}\) the Yosida regularization of the indicator function of the cone \(C = \{ v \in {\mathbb {R}}^3: v \cdot n^+ \le 0 \} \) (cf. also Remark 8.3);
-
(ii)
\(\gamma (z) = \max \{ z,0\}\);
-
(iii)
\({{\widehat{\phi }}}\) encompassing the indicator function \(I_{[0,1]}\), which ensures \(z \in [0,1]\);
-
(iv)
\(\psi (\llbracket u \rrbracket ) = \tfrac{k}{2} |\llbracket u \rrbracket |^2\) with \(k>0\).
Observe that (8.4) falls into the class of gradient systems (4.11), with the ambient spaces
where \({\textrm{H}}_{\Gamma _{{\textrm{D}}}}^1(\Omega ;{\mathbb {R}}^3)\) the space of \({\textrm{H}}^1\)-functions on \(\Omega \) fulfilling a homogeneous Dirichlet boundary condition on \(\Gamma _{{\textrm{D}}}\). By Korn’s inequality, the quadratic form associated with the operator \({{\textbf { D}}}\) induces on \({\textbf{U}}\) a norm equivalent to the \(\mathrm {\textrm{H}}^1\)-norm; hereafter, we will in fact use that

The 1-homogeneous dissipation potential \({{\mathcal {R}}}: {\textbf{Z}}\rightarrow [0,\infty )\) is defined by
The viscous dissipation potentials \({{\mathcal {V}}}_{\textsf{u}} : {\textbf{U}}\rightarrow [0,\infty )\) and \({{\mathcal {V}}}_{\textsf{z}} : {\textbf{U}}\rightarrow [0,\infty )\) are

The driving energy functional \({{\mathcal {E}}}: [0,T]{\times }{\textbf{U}}{\times }{\textbf{Z}}\rightarrow (\infty ,+\infty ]\) is given by

and \(\infty \) otherwise.
As we will see in Proposition 8.2, under the conditions on \({{\widehat{\beta }}}\), \(\gamma \), \({{\widehat{\phi }}}\), and \(\psi \) specified in (8.5), \({{\mathcal {E}}}\) complies with the coercivity conditions from Hypothesis 4.3 with the spaces
and its Fréchet subdifferential \(\partial _q {{\mathcal {E}}}: [0,T] {\times }{\textbf{U}}{\times }{\textbf{Z}}\rightrightarrows {\textbf{U}}^* {\times }{\textbf{Z}}^*\) is given by
(indeed, observe that, by the growth properties of \(\gamma \) and \(\psi \), the term \( \omega \psi (\llbracket u \rrbracket ) \) is in \({\textrm{L}}^2(\Gamma _{{\textrm{C}}})\) for any selection \(\omega \in \partial \gamma \)). In particular, here we have used that the Fréchet subdifferential of the (\(({-}\Lambda _\phi )\)-convex) functional \({{\mathcal {F}}}: {\textbf{Z}}\rightarrow [0,\infty ]\)

is given by
We also point out for later use that \(\partial _{\textsf{q}}{{\mathcal {E}}}\) fulfills the structure condition (4.23), i.e. \( \partial _{\textsf{q}}{{\mathcal {E}}}(t,u, z) =\partial _{\textsf{u}}{{\mathcal {E}}}(t,u, z) {\times }\partial _{\textsf{z}}{{\mathcal {E}}}(t,u, z) \) for every \((t,u,z) \in [0,T]{\times }{\textbf{U}}{\times }{\textbf{Z}}\).
8.1.2 Existence for the Viscous System
As we will check in Proposition 8.2 ahead, our general existence result, Theorem 4.8, applies to the viscous delamination system. Hence, for every pair of initial data \((u_0,z_0) \in {\textrm{H}}_{\Gamma _{{\textrm{D}}}}^1(\Omega ;{\mathbb {R}}^3) {\times }{\textrm{H}}^1(\Gamma _{{\textrm{C}}})\) there exists a solution
to the Cauchy problem for system (8.4).
8.2 The Vanishing-Viscosity Limit
We will now address the vanishing-viscosity limit as \(\varepsilon \rightarrow 0^+\) of system (8.4). Our main result states the convergence of (a selected family of) viscous solutions to an enhanced \(\text {BV}\) solution to the system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) defined by (8.6), in fact enjoying the additional regularity \(z\in \text {BV}([0,T];{\textbf{Z}}_{{\textrm{e}}})\) (with \({\textbf{Z}}_{{\textrm{e}}}= \mathrm {\textrm{H}}^1(\Gamma _{{\textrm{C}}})\)). Analogously, we also obtain the existence of parametrized \(\text {BV}\) solutions, to which Theorem 5.21 applies, providing a characterization in terms of system (8.15) ahead.
In fact, we will be able to obtain solutions to the viscous system (8.4) enjoying estimates, uniform with respect to the viscosity parameter, suitable for the vanishing-viscosity analysis, only by performing calculations on a version of system (8.4) in which the functions \({{\widehat{\beta }}}\), \(\gamma \), \({{\widehat{\phi }}}\), and \(\psi \) are suitably smoothened, cf. (8.18). That is why, in Theorem 8.1 below will state:
-
(i)
the existence of qualified viscous solutions to (the Cauchy problem for) (8.4), where by ‘qualified’ we mean enjoying estimates (8.13) below;
-
(ii)
their convergence (up to a subsequence) to an enhanced \(\text {BV}\) solution (we mention that, since the viscous dissipation potentials from (8.6c) are both 2-homogeneous, the formulas in (5.11) and (5.14) yield an explicit representation formula for the functional \({\mathfrak {M}}_{0}^{\alpha }\) involved in the definition of \(\text {BV}\) solution);
-
(iii)
the convergence of reparametrized (qualified) viscous solutions to an enhanced \(\text {pBV}\) solution for which the differential characterization from Theorem 5.21 holds.
For simplicity, in Theorem 8.1 we shall not consider a sequence of initial data \((u_0^\varepsilon ,z_0^\varepsilon )_{\varepsilon }\) but confine the statement to the case of fixed data \((u_0,z_0)\). We will impose that \((u_0,z_0)\) fulfill the additional ‘compatibility condition’ (8.11).
Theorem 8.1
Assume conditions (8.3) and (8.5). Let \((u_0,z_0) \in {\textbf{U}}\times {\textbf{Z}}_{{\textrm{e}}}\) fulfill
Then, there exists a family
solving the Cauchy problem for the viscous delamination system (8.10) with the initial data \((u_0,z_0)\), and enjoying the following estimate
Moreover, for any null sequence \((\varepsilon _k)_k\) the sequence \((u_{\varepsilon _k},z_{\varepsilon _k})_k \) admits a (not relabeled) subsequence, and there exists a pair
such that
-
(1)
the following convergences hold as \(k\rightarrow \infty \)
$$\begin{aligned} u_{\varepsilon _k}(t) \rightharpoonup u(t)\;\text {in}\; {\textrm{H}}_{\Gamma _{{\textrm{D}}}}^1(\Omega ;{\mathbb {R}}^3), \quad z_{\varepsilon _k}(t) \rightharpoonup z(t)\;\text {in}\; {\textrm{H}}^1(\Gamma _{{\textrm{C}}}) \quad \text {for all}\; t \in [0,T];\nonumber \\ \end{aligned}$$(8.14) -
(2)
(u, z) is an enhanced \(\text {BV}\) solution to the delamination system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) from (8.6).
Finally, reparametrizing the sequence \((u_{\varepsilon _k},z_{\varepsilon _k})_k \) in such a way that the rescaled curves \(({\textsf{t}}_{\varepsilon _k}, {\textsf{u}}_{\varepsilon _k}, {\textsf{z}}_{\varepsilon _k})_k\) enjoy estimates (5.29) and (5.37), up to a subsequence we have convergence of \(({\textsf{t}}_{\varepsilon _k}, {\textsf{u}}_{\varepsilon _k}, {\textsf{z}}_{\varepsilon _k})_k\), in the sense of (5.31), to an enhanced \(\text {pBV}\) solution \(({\textsf{t}},{\textsf{u}},{\textsf{z}}): [0,{{{\textsf {S}}}}] \rightarrow [0,T]{\times }{\textrm{H}}_{\Gamma _{{\textrm{D}}}}^1(\Omega ;{\mathbb {R}}^3){\times }{\textrm{H}}^1(\Gamma _{{\textrm{C}}})\) for which the differential characterization from Theorem 5.21 holds. Namely, there exist measurable functions \(\lambda _{\textsf{u}},\, \lambda _{\textsf{z}}: (0,{{{\textsf{S}}}})\rightarrow [0,\infty ] \) satisfying for almost all \(s\in (0,{{{\textsf{S}}}})\) the switching conditions (5.49c) and the subdifferential inclusions
(with convention (5.43) in the case \(\lambda _{\textsf{x}}(s) = \infty \)).
Proof
It is sufficient to check that the system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) from (8.6) complies with the assumptions of Theorems 5.15, 5.21, and 6.12, and that there exist ‘qualified’ viscous solutions enjoying estimates (8.13). More precisely,
-
(1)
In Proposition 8.2 ahead we will check that the rate-independent delamination system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) complies with Hypotheses 4.1, 4.2, 4.3, 4.5, 4.10, and 5.8 (in fact, the parametrized chain rule (5.40) holds).
-
(2)
We will obtain the existence of viscous solutions enjoying estimates (8.13) by working on a smoothened version of system (8.4), introduced in Sect. 8.4 ahead. Therein, we will obtain estimates for the solutions to the regularized viscous system uniform with respect to the regularization parameter. Hence, with Proposition 8.5 in Sect. 8.5 we will conclude the existence of ‘qualified’ solutions for which (8.13) holds, and thereby conclude the proof of Theorem 8.1.
\(\square \)
In what follows, we will most often use the place-holders \({\textbf{U}}\), \({\textbf{Z}}\),... (cf. (8.6a) and (8.7)) for the involved function spaces.
8.3 Properties of the Rate-Independent System for Delamination
This section is centered around Proposition 8.2 below, in which we check the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) from (8.6). complies with the ‘abstract’ Hypotheses from Sect. 4. In particular, from the following result we gather that Theorem 4.8 is applicable, yielding the existence of solutions as in (8.10) to the viscous delamination system.
Proposition 8.2
Assume (8.3) and (8.5). Then, the delamination system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) from (8.6) fulfills Hypotheses 4.1, 4.2, 4.3, 4.5, 4.10, and 5.8.
Proof
The proof consists of three steps.
\(\underline{\textit{Step 1. Hypotheses 4.1, 4.2, 4.3, and 4.10:}}\) The validity of Hypothesis 4.1, 4.2, and 4.3 is obvious. A straightforward calculation shows that the Fréchet subdifferential of \({{\mathcal {E}}}\) is given by (8.8), so that the structure condition \(\partial _{\textsf{q}}{{\mathcal {E}}}(t,q) = \partial _{\textsf{u}}{{\mathcal {E}}}(t,q) {\times }\partial _{\textsf{z}}{{\mathcal {E}}}(t,q)\) holds at every \(q=(u,z) \in {\textbf{U}}\times {\textbf{Z}}\). Therefore, by Lemma 4.11, Hypothesis 4.10 will be ensured by the validity of Hypothesis 4.5, which we now check.
\(\underline{\textit{Step 2. Hypothesis 4.5:}}\) Let \((t_n)_n \subset [0,T]\) and \((u_n,z_n)_n\subset {\textbf{U}}{\times }{\textbf{Z}}\) be in the conditions of Hypothesis 4.5, and let \((\mu _n,\zeta _n)_n\), with \(\mu _n \in \partial _{\textsf{u}}{{\mathcal {E}}}(t_n,u_n, z_n) \) and \(\zeta _n \in \partial _{\textsf{z}}{{\mathcal {E}}}(t_n,u_n, z_n) \), fulfill \(\mu _n \rightharpoonup \mu \) in \({\textbf{U}}^*\) and \(\zeta _n\rightharpoonup \zeta \) in \({\textbf{Z}}^*\). Hence,
We observe that, by Sobolev embeddings and trace theorems, from the convergences \(u_n\rightharpoonup u \) in \({\textbf{U}}_{{\textrm{e}}}\) and \(z_n\rightharpoonup z\) in \({\textbf{Z}}_{{\textrm{e}}}\) we infer that \(\llbracket u_n \rrbracket \rightarrow \llbracket u \rrbracket \) in \({\textrm{L}}^{q}(\Gamma _{{\textrm{C}}};{\mathbb {R}}^3)\) for all \(1\le q<4\), and \(z_n\rightarrow z \) in \({\textrm{L}}^p(\Gamma _{{\textrm{C}}})\) for all \(1\le p<\infty \). Furthermore, since \(0 \le z_n \le 1 \) a.e. on \(\Gamma _{{\textrm{C}}}\), we even have \(z_n\overset{*}{\rightharpoonup }z\) in \({\textrm{L}}^\infty (\Gamma _{{\textrm{C}}})\). Since \(\gamma \) is Lipschitz, we gather that \(\gamma (z_n) \rightarrow \gamma (z)\) in \({\textrm{L}}^p(\Gamma _{{\textrm{C}}})\) for all \(1\le p<\infty \), too. By the growth properties of \(\psi \), we have that the sequence \((\varrho _n)_n\) with \(\varrho _n \in \partial \psi (\llbracket u_n \rrbracket )\) a.e. in \(\Gamma _{{\textrm{C}}}\) is bounded in \({\textrm{L}}^4(\Gamma _{{\textrm{C}}})\) and thus, up to a subsequence, it weakly converges in \({\textrm{L}}^4(\Gamma _{{\textrm{C}}})\) to some \(\varrho \). By the strong-weak closedness of the graph of \(\partial \psi \) (or, rather, of the maximal monotone operator that \(\partial \psi : {\mathbb {R}}^3 \rightrightarrows {\mathbb {R}}^3\) induces on \({\textrm{L}}^{2}(\Gamma _{{\textrm{C}}})\)), we have that \(\varrho \in \partial \psi (\llbracket u \rrbracket )\) a.e. in \(\Gamma _{{\textrm{C}}}\). Moreover, we find that \(\gamma (z_n)\varrho _n \rightharpoonup \gamma (z) \varrho \), for instance in \({\textrm{L}}^2(\Gamma _{{\textrm{C}}})\). Since \(\beta \) is Lipschitz, we also have \(\beta (\llbracket u_n \rrbracket )\rightarrow \beta (\llbracket u \rrbracket )\) in \({\textrm{L}}^{q}(\Gamma _{{\textrm{C}}};{\mathbb {R}}^3)\) for all \( 1\le q<4\). Also taking into account that \(\ell _u \in {\textrm{C}}^1([0,T];{\textbf{U}}^*)\), we then conclude the weak limit \(\mu \) of the sequence \((\mu _n)_n\) belongs to \(\partial _{\textsf{u}}{{\mathcal {E}}}(t,q)\).
Let us now discuss the weak \({\textbf{Z}}\)-limit \(\zeta \) of the sequence \((\zeta _n)_n\). First of all, from the Lipschitz continuity of \(\gamma \) we gather that the sequence \((\omega _n)_n\) is bounded in \({\textrm{L}}^\infty (\Gamma _{{\textrm{C}}})\). Hence, \( (\omega _n \psi (\llbracket u_n \rrbracket ) )_n\) is bounded in \({\textrm{L}}^2(\Gamma _{{\textrm{C}}})\) and, a fortiori, we gather that also the terms \( ({{\textbf { A}}}z_n + \phi _n)_n\) are bounded in \({\textrm{L}}^2(\Gamma _{{\textrm{C}}})\). By the strong-weak closedness of the graph of (the operator induced by) \(\partial \gamma \) (on \({\textrm{L}}^2(\Gamma _{{\textrm{C}}})\)), we infer that \(\omega \in \partial \gamma (z)\) a.e. in \(\Gamma _{{\textrm{C}}}\). Since \(\psi \) has at most quadratic growth, from \(\llbracket u_n \rrbracket \rightarrow \llbracket u \rrbracket \) in \({\textrm{L}}^{q}(\Gamma _{{\textrm{C}}};{\mathbb {R}}^3)\) for all \(1\le q<4\) we obtain that \(\psi (\llbracket u_n \rrbracket )\rightarrow \psi (\llbracket u \rrbracket )\) in \({\textrm{L}}^{q/2}(\Gamma _{{\textrm{C}}};{\mathbb {R}}^3)\) via the dominated convergence theorem. All in all, we have that \(\omega _n \psi (\llbracket u_n \rrbracket ) \rightharpoonup \omega \psi (\llbracket u \rrbracket ) \in \psi (\llbracket u \rrbracket ) \partial \gamma (z)\) in \({\textrm{L}}^2(\Gamma _{{\textrm{C}}})\).
In turn, also taking into account that the sequence \(({{\textbf { A}}}z_n)_n\) is itself bounded in \({\textrm{H}}^1(\Gamma _{{\textrm{C}}})^*\), it is immediate to check that there exists \(\phi \in {\textrm{H}}^1(\Gamma _{{\textrm{C}}})^*\) such that \({{\textbf { A}}}z_n + \phi _n\rightharpoonup {{\textbf { A}}}z + \phi \) in \({\textrm{L}}^2(\Gamma _{{\textrm{C}}})\). Since the functional \({{\mathcal {F}}}\) from (8.9) \({{\mathcal {F}}}\) is also \(({-\Lambda _\phi })\)-convex, its Fréchet subdifferential has a strongly-weakly closed graph in \({\textrm{L}}^2(\Gamma _{{\textrm{C}}}) {\times }{\textrm{L}}^2(\Gamma _{{\textrm{C}}})\), and we thus infer that \(\phi \in \partial \widehat{\phi }(z) \) a.e. in \(\Gamma _{{\textrm{C}}}\). All in all, we conclude that that \(\zeta \in \partial _{\textsf{z}}{{\mathcal {E}}}(t,q)\). This concludes the proof of Hypothesis 4.5.
\(\underline{\textit{Step 3. Hypothesis 5.8:}}\) Let us now turn to the parametrized chain rule from Hypothesis 5.8. Since the viscous dissipation potentials are 2-homogeneous, the associated vanishing-viscosity contact potentials are given by (3.12) (cf. Example 3.5) so that, in particular, the coercivity condition (5.39) holds, and Proposition 5.17 is applicable. Therefore, Hypothesis 5.8 follows from the chain rule of Hypothesis 4.7. The latter chain-rule property can be verified by resorting to Proposition A.1 ahead. Hence, we need to show \({{\mathcal {E}}}\) complies with condition (A.1), which states that the Fréchet subdifferential \(\partial _q {{\mathcal {E}}}\) can be characterized by a global inequality akin to that defining the convex analysis subdifferential: for every \(E>0\), and energy sublevel \({\mathcal {S}}_{E}\), there exists an upper semicontinuous function \(\varpi ^E: [0,T]{\times }{\mathcal {S}}_{E} {\times }{\mathcal {S}}_{E}\rightarrow [0,\infty ]\), with \(\varpi ^E(t,q,q) =0 \) for every \(t \in [0,T]\) and \( q \in {\mathcal {S}}_{E}\), such that

In order to check (8.16), we will resort to a decomposition for the energy functional from (8.6d) as
with \({{\mathcal {F}}}\) from (8.9),

while, for later convenience, we encompass the surface term \(\int _{\Gamma _{{\textrm{C}}}} {\widehat{\beta }}(\llbracket u \rrbracket ) \,\,\!{\textrm{d}}x\) in the coupling energy
Now, \({{\mathcal {E}}}_{{\textrm{elast}}}(t,\cdot )\) is convex while \({{\mathcal {F}}}\) is \((-\Lambda _\phi )\)-convex. Hence, they both comply with (8.16). Hence, it is sufficient to check its validity for \({{\mathcal {E}}}_{{\textrm{coupl}}}\), and indeed for its second contribution, only, since \(\widehat{\beta }\) is also convex. Indeed, for every \({{\hat{u}}}, \, u \in {\textbf{U}}\) and \({{\hat{z}}},\, z \in {\textbf{Z}}\) and for all selections \(\Gamma _{{\textrm{C}}}\ni x \mapsto \varrho (x) \in \partial \psi (\llbracket u(x) \rrbracket )\) and \( \Gamma _{{\textrm{C}}}\ni x \mapsto \omega (x) \in \partial \gamma (z(x)) \) there holds
where (1) & (2) follow from the convexity of \(\gamma \) and \(\psi \), respectively, whereas (3) is due to the 1-Lipschitz continuity of \(\gamma \). Then, estimate (8.16) follows with the function \(\varpi _t^E({{\hat{q}}}, q): = \Vert \psi (\llbracket {{\hat{u}}} \rrbracket ){-}\psi (\llbracket u \rrbracket )\Vert _{{\textrm{L}}^2(\Gamma _{{\textrm{C}}})}\). We have thus checked the validity of (8.16) and, a fortiori, of Hypothesis 5.8. This concludes the proof. \(\square \)
Remark 8.3
The Lipschitz continuity of \(\beta \) has played a key role in the proof that \({{\mathcal {E}}}\) complies with the closedness condition from Hypothesis 4.5. In fact, we could allow for a nonsmooth \({{\widehat{\beta }}}\), but with a suitable polynomial growth condition, that would still ensure that the maximal monotone operator induced by \(\beta = \partial \widehat{\beta }\) on \({\textrm{L}}^2(\Gamma _{{\textrm{C}}})\) is strongly-weakly closed. However, it would not be possible to check Hypothesis 4.5 in the case \(\beta \) is an unbounded maximal monotone operator, such as the subdifferential of an indicator function. That is why, we are not in a position to encompass in our analysis the non-interpenetration constraint between the two bodies \(\Omega ^+\) and \(\Omega ^-\).
8.4 A Priori Estimates for the Smooth Semilinear System
In this section we address a version of the viscous system (8.4) in which the functions \({{\widehat{\beta }}}\), \(\gamma \), \({{\widehat{\phi }}}\), and \(\psi \), complying with (8.5), are also smoothened. Namely, we will additionally suppose that they fulfill
These conditions will allow us to rigorously perform, on the solutions to system (8.4), calculations that will ultimately lead to bounds, uniform with respect to viscosity parameter, suitable for our vanishing-viscosity analysis. Such estimates will however only depend on the constants occurring in (8.5), and not on those in (8.18). For these calculations we will crucially make use of the semilinear structure of this regularized system and of the fact that the coupling between the displacement equation and the flow rule for the delamination parameter is weak enough to allow us to treat those equations separately.
As already mentioned, for all \(\varepsilon \in (0,1)\) and all initial data \((u_0,z_0)\in {\textbf{U}}{\times }{\textbf{Z}}_{{\textrm{e}}}\) system (8.4) admits finite-energy solutions \((u_\varepsilon ,z_\varepsilon )\) with the standard time regularity (8.10). We now aim to derive higher order estimates as well, and to show that these estimates are independent of \(\varepsilon \). We will make them as explicit as possible. Let us mention in advance that one crucial argument involves the interpolation between the different norms for the time derivative \(\dot{z}\), namely
Indeed, (8.19) follows by combining the lower bound \({{\mathcal {R}}}(v)\ge c_R\Vert v\Vert _{{\textrm{L}}^1}\) with the classical Gagliardo-Nirenberg interpolation \(\Vert v\Vert _{{\textrm{L}}^2}^2 \le C \Vert v\Vert _{{\textrm{L}}^1} \Vert v\Vert _\mathrm{{\textrm{H}}^1}\). This will allows us to exploit the \(\varepsilon \)-independent dissipation estimate \(\int _0^T {{\mathcal {R}}}(\dot{z}_\varepsilon )\,\,\!{\textrm{d}}t \le C\).
\(\underline{\textit{Step 1. Basic energy and dissipation estimates:}}\) The simple energy-dissipation estimate stemming from the energy balance (4.18b) (cf. Lemma 4.12), together with \(\ell _u \in {\textrm{C}}^1([0,T;{\textbf{U}}^*)\) implies that for all \(E_0\) there exists \(C^{E_0}_1>0\) such that all solutions \((u_\varepsilon ,z_\varepsilon )\) of (8.4) with \({{\mathcal {E}}}(0,u_\varepsilon (0),z_\varepsilon (0)\le E_0\) satisfy the basic energy estimates
As a consequence of this a priori bound, of the fact that \({\varvec{J}}: {\textbf{U}}\rightarrow {\textrm{L}}^4(\Gamma _{{\textrm{C}}};{\mathbb {R}}^3)\) is a bounded operator, and of upper estimates on \(\psi \) via the constants \(C_\psi \) and \(C^{(1)}_\psi \), we find another constant \(C^{E_0}_2\) such that all solutions \((u_\varepsilon ,z_\varepsilon )\) of (8.4) with \({{\mathcal {E}}}(0,u_\varepsilon (0),z_\varepsilon (0))\le E_0\) satisfy
Estimate (8.21b) will in fact only be used for gaining enhanced regularity of the viscous solutions \((u_\varepsilon ,z_\varepsilon )\), and not for the vanishing-viscosity analysis.
\(\underline{\textit{Step 2. Estimate for }\dot{u}_\varepsilon :}\) Because of the smoothness of \(\widehat{\beta }\) and \(\psi \), the displacement equation (8.4a) for \(u_\varepsilon \) is a semilinear equation with a smooth nonlinearity, if we consider \(z_\varepsilon \in \mathrm {\textrm{H}}^1(0,T;{\textbf{Z}})\) as given datum. Thus, we can use the classical technique of difference quotients to show that \(u_\varepsilon \in \mathrm {\textrm{H}}^2(0,T;{\textbf{U}})\) provided that \(\dot{u}_\varepsilon (0)= \varepsilon ^{-\alpha }{{\textbf { D}}}^{-1}\big ({{\textbf { C}}}u(0)+{\varvec{J}}^*(\cdots )-\ell _u(0)\big ) \in {\textbf{U}}\). Hence, it is possible to differentiate (8.4a) with respect to time, which yields
We can test (8.22) by \(\dot{u}_\varepsilon \in \mathrm {\textrm{H}}^1(0,T;{\textbf{U}})\) and obtain
Here the last duality product in the first line is nonnegative, because \(a\mapsto \widehat{\beta }(a) + \gamma (z)\psi (a)\) is convex. The last duality product can be estimated using (8.21a). Defining \({\varvec{\theta }}^\varepsilon _{\textbf{U}}\), \({\varvec{\theta }}^\varepsilon _{\textbf{Z}}\), and \(\lambda _{{\textbf{U}}^*}\) via
we have established the estimate
where we have also used that \(\gamma \) is 1-Lipschitz continuous, and \( C_\mathrm{{\textrm{H}}^1,{\textrm{L}}^4} \) denotes the constant associated with the continuous embedding \({\textbf{U}}\subset {\textrm{L}}^4(\Gamma _{{\textrm{C}}};{\mathbb {R}}^3)\). Using \(\frac{{\textrm{d}}}{{\textrm{d}}t}({\varvec{\theta }}^\varepsilon _{\textbf{U}})^2= 2 {\varvec{\theta }}^\varepsilon _{\textbf{U}}\,{\dot{{\varvec{\theta }}}}^\varepsilon _{\textbf{U}}\) we can divide by \( {\varvec{\theta }}^\varepsilon _{\textbf{U}}\ge 0\) and obtain
Let us mention that the above estimate could be rigorously obtained by replacing \( {\varvec{\theta }}^\varepsilon _{\textbf{U}}\) by \(\sqrt{ ({\varvec{\theta }}^\varepsilon _{\textbf{U}})^2 +\delta }\), which satisfies the same estimate, and then letting \(\delta \downarrow 0\), cf. [30, Sec. 4.4].
\(\underline{\textit{Step 3. Uniqueness and higher regularity of }\dot{z}_\varepsilon :}\) We first observe that given \(u_\varepsilon \in \mathrm {\textrm{H}}^1([0,T];{\textbf{U}})\) and \(z_0\) there is a unique solution \(z_\varepsilon \) for (8.4b). Indeed, assuming that \(z_1\) and \(z_2\) are solutions (with \(\varrho _j \in \partial {\textrm{R}}(\dot{z}_j))\) we set \(w=z_1{-}z_2\) and test the difference of the two equations by \(\dot{w}=\dot{z}_1{-}\dot{z}_2\), which yields

where we have set \(G(u,z)=\widehat{\phi }'(z) + \gamma '(z)\psi (\llbracket u \rrbracket )\). By our strengthened assumptions (8.18) and Gagliardo-Nirenberg interpolation we have
By using the monotonicity of \(\partial {\textrm{R}}\), the first term in (8.24) is nonnegative. Using  we obtain
we obtain
Canceling the terms \(\varepsilon \Vert \dot{w}\Vert _{\textbf{Z}}^2\) and using \(\Vert w\Vert _{\textbf{Z}}\le \Vert w\Vert _{{\textbf{Z}}_{{\textrm{e}}}}\) provides the estimate
We emphasize that this uniqueness result is special and relies strongly on the semilinear structure of the flow rule for z under the strengthened assumption (8.18). It is indeed thanks to (8.18) that \(G(u,\cdot ):{\textbf{Z}}_{{\textrm{e}}}\rightarrow {\textbf{Z}}^*\) is globally Lipschitz, and in fact the constant \(C_G\) in (8.25) does depend on \( C^{(1)}_\psi \).
This uniqueness is central to derive higher regularity as it is now possible to use suitable regularizations such as Galerkin approximations or replacing the nonsmooth function \({\textrm{R}}\) by a smoothed version \({\textrm{R}}_\delta \). We do not go into detail here, but refer to [36] and [30, Sec. 4.4]. In particular, our problem fits exactly into the abstract setting of [36, Sec. 3] with \(H={\textbf{Z}}={\textrm{L}}^2(\Gamma _{{\textrm{C}}})\), \({\mathcal {B}}={{\textbf { A}}}\), and \(\Phi (t,z)= \int _\Omega \big (\widehat{\phi }(z)+ \gamma (z) \psi (\llbracket u(t) \rrbracket \big ) \,\,\!{\textrm{d}}x\).
Thus, under the additional condition \({{\textbf { A}}}z_0\in {\textbf{Z}}\) (or \(z_0\in \mathrm {\textrm{H}}^2(\Gamma _{{\textrm{C}}})\)), the unique solution \(z_\varepsilon \) with \(z_\varepsilon (0)=z_0\) satisfies the following higher regularity properties:
Of course, at this stage we have no control over the dependence on \(\varepsilon \) of the corresponding norms.
\(\underline{\textit{Step 4. Identities not involving}\,{\textrm{R}}:}\) Surprisingly, there are two identities for the solution \(z_\varepsilon \) that are completely independent of \({\textrm{R}}\), i.e. they look like energy estimates for a semilinear parabolic problem:


We refer to [30, Eqn. (95) and Lem. 4.16] for a rigorous derivation based on the smoothness established in (8.26). Relations (8.27) can be formally derived from equation (8.4b) by forgetting the nonsmooth term \(\partial {\textrm{R}}\), then differentiating the whole equation with respect to t, and finally testing with \(\dot{z}_\varepsilon \) or \(\ddot{z}_\varepsilon \) respectively. Indeed, (8.27b) will not be used below any more, but its relevance is obvious by comparison with (8.24) and for deriving the (\(\varepsilon \)-dependent) a priori estimate for \(\sqrt{t\,}\,\ddot{z}_\varepsilon \) (via Galerkin approximations).
It is the identity (8.27a) that will be crucial for deriving \(\varepsilon \)-independent a priori estimates. It origin can formally understood by looking at general smooth p-homogeneous dissipation potentials \({\varvec{\Psi }}\) (i.e. fulfilling \({\varvec{\Psi }}(\gamma v)=\gamma ^p{\varvec{\Psi }}(v)\) for all v and \(\gamma >0\)). Then, Euler’s formula gives \(\langle {\textrm{D}}{\varvec{\Psi }}(v),v\rangle = p {\varvec{\Psi }}(v) \), and we find the identity
The quadratic case \(p=2\) was applied above several times. Of course, in the case \(p=1\) the potential \({{\mathcal {R}}}\) is nonsmooth. Hence, the proof in [30, Lem. 4.16] is different and uses simple arguments based on the characterization of \(\partial {{\mathcal {R}}}\) in the 1-homogeneous case.
\(\underline{\textit{Step 5. }{\textrm{L}}^1\textit{ estimates for }{\varvec{\theta }}^\varepsilon _{\textbf{U}}, {\varvec{\theta }}^\varepsilon _{\textbf{Z}},\textit{ and }{\varvec{\theta }}^\varepsilon _{{\textbf{Z}}_{{\textrm{e}}}}:}\) In (8.27a) the coupling term \( \langle {\textrm{D}}_z{\textrm{D}}_u \Phi (u_\varepsilon ,z_\varepsilon )\dot{u}_\varepsilon , \dot{z}_\varepsilon \rangle \) can be estimated via the weaker assumption (8.5), namely

where we exploited the 1-Lipschitz continuity of \(\gamma \) and (8.21a). Introducing the short-hand notation \({\varvec{\theta }}^\varepsilon _{{\textbf{Z}}_{{\textrm{e}}}}\) via  and exploiting the \(\Lambda _\phi \)-convexity of \(\widehat{\phi }\) and the convexity of \(\gamma \), identity (8.27a) yields
and exploiting the \(\Lambda _\phi \)-convexity of \(\widehat{\phi }\) and the convexity of \(\gamma \), identity (8.27a) yields
For the first term on the right-hand side we can now exploit the interpolation (8.19) and after division by \({\varvec{\theta }}^\varepsilon _{\textbf{Z}}\ge 0\) (recall \({\varvec{\theta }}^\varepsilon _{\textbf{Z}}\le {\varvec{\theta }}^\varepsilon _{{\textbf{Z}}_{{\textrm{e}}}}\)) we arrive, together with (8.23), at the differential estimates
We emphasize that all the appearing coefficients, except for the leading factors \(\varepsilon ^\alpha \) and \(\varepsilon \), are independent of \(\varepsilon \in (0,1)\) and indeed depend only on \(C_\psi \). From the first equation we obtain via the constants-of-variation formula (or Grönwall’s lemma) the estimate
Because of \(\Vert K_\varepsilon \Vert _{{\textrm{L}}^1} = \int _0^\infty K_\varepsilon (t)\,\,\!{\textrm{d}}t =1/c_{{{\textbf { C}}}}\) the \({\textrm{L}}^1\)-convolution estimate leads to
Applying the Cauchy–Schwarz inequality to the last integral and integrating (8.28b) over [0, T] we obtain the estimates
From this it is easy to show that there exists a constant \(C_*\), which only depends on \(C_3 =C_\psi C^{E_0}_2 C_\mathrm{{\textrm{H}}^1,{\textrm{L}}^4} \Vert {\varvec{J}}\Vert \), \(c_{{{\textbf { C}}}}\), \(C_\text {GN}\), and \(\Lambda _\phi \), such that \(I_{\textbf{U}}{+}I_{{\textbf{Z}}_{{\textrm{e}}}}\) can be estimated by \(C_*\big (\varepsilon ^\alpha {\varvec{\theta }}^\varepsilon _{\textbf{U}}(0) + \varepsilon {\varvec{\theta }}^\varepsilon _{\textbf{Z}}(0) +\int _0^T\lambda _{{\textbf{U}}^*}\,\,\!{\textrm{d}}t +I_R\big ) \). We are thus able to prove the crucial \({\textrm{L}}^1\)-bound.
Proposition 8.4
(Rate-independent a priori estimate in the semilinear case) Assume (8.3) and (8.5). Additionally, let \({{\widehat{\beta }}}\), \(\gamma \), \({{\widehat{\phi }}}\), and \(\psi \) satisfy (8.18) and let the initial data \((u_0,z_0) \in {\textbf{U}}\times {\textbf{Z}}_{{\textrm{e}}}\) comply with (8.11). Then, there exists a constant \(C_*>0\), only depending on the initial data and on the constants \(\Lambda _\phi \) and \(C_\psi \) from (8.5), such that the unique solution \((u_\varepsilon ,z_\varepsilon )\) of (8.4) satisfies the a priori estimate
8.5 Existence and a Priori Estimates in the General Case
We now return to the setup of Sects. 8.1 and 8.2, in which the constitutive functions \(\widehat{\beta }\), \(\gamma \), \(\widehat{\phi }\), and \(\psi \) only comply with (8.5). We exhibit approximations of \(\widehat{\beta }\), \(\gamma \), \(\widehat{\phi }\), and \(\psi \) that also satisfy (8.18). For this, we will resort to the following general construction.
Smoothening the Yosida Approximation. Following, e.g., the lines of [17, Sec. 3], for a given convex function \({\widehat{\chi }}: {\mathbb {R}}^d \rightarrow [0,\infty ]\) with subdifferential \(\chi = \partial \widehat{\chi }: {\mathbb {R}}^d \rightrightarrows {\mathbb {R}}^d\), and for a fixed \(\delta \in (0,1)\), we define
where \( \chi _\delta ^{{\textrm{Y}}} \) is the Yosida regularization of the maximal monotone operator \(\chi \) (we refer to, e.g., [7]) and
Thus, \(\chi ^\delta \in {\textrm{C}}^\infty ({\mathbb {R}}^d)\) and it has been shown in [17] that
Taking into account the properties of the Yosida regularization we deduce that
Furthermore, \(\chi ^\delta \) admits a convex potential \({{\widehat{\chi }}}^\delta \) satisfying, as a consequence of (8.31a), (below \(\widehat{\chi }_\delta ^{{\textrm{Y}}}\) denotes the Yosida approximation of \(\widehat{\chi }\)):

Finally, the following analogue of Minty’s trick holds: given \(O \subset {\mathbb {R}}^m\), a sequence \((v_\delta )_\delta \), and limits \(v,\, \chi \in {\textrm{L}}^2 (O;{\mathbb {R}}^d)\) such that \(v_\delta \rightharpoonup v\) and \(\chi ^\delta (v_\delta ) \rightharpoonup \eta \) in \( {\textrm{L}}^2 (O;{\mathbb {R}}^d)\), then
We apply this construction to \(\gamma \), obtaining a smooth approximation \(\gamma ^\delta \). The definition of \(\widehat{\beta }^\delta \) clearly simplifies, since we have already required that \(\widehat{\beta }\in {\textrm{C}}^1({\mathbb {R}})\) with \(\beta \) Lipschitz. As for \(\phi \), we define
with \(f^\delta \) the smoothened Yosida approximation of the convex function \(z\mapsto f(z)= \widehat{\phi }(z) +\frac{\Lambda _\phi }{2}z^2 \). It follows from (8.31a) that \(\widehat{\beta }^\delta \), \(\gamma ^\delta \) and \( \phi ^\delta \) comply with (8.18).
The Construction of \(\psi ^\delta \). In smoothening \(\psi \) we also have to take care of the linear growth constraint encompassed in (8.18). Hence, we construct \(\psi ^\delta \) in two steps:
\(\underline{\textit{Step 1. Inf-convolution}}\) We define \(\psi _\delta ^{{\textrm{ic}}}: {\mathbb {R}}^3 \rightarrow [0,\infty )\) via inf-convolution with the smooth function \(h:{\mathbb {R}}^3 \rightarrow [0,\infty )\), \(h(a): = \sqrt{1{+}|a|^2}-1\) by setting
It turns out that \(\psi _\delta ^{{\textrm{ic}}}\) is convex, of class \({\textrm{C}}^1\), and since \(h(0)=0\) we have that

Since h is even, we also have \(\psi _\delta ^{{\textrm{ic}}}(a) = \inf _{x\in {\mathbb {R}}^3} \{ \tfrac{1}{\delta }h(x)+\psi (a{-}x)\}\). Hence, recalling that \(\psi (0)=0\) we find that

so that, in particular, \(\psi _\delta ^{{\textrm{ic}}}\) has linear growth. Finally, let \(a_\delta \in \mathop {{\textrm{Argmin}}}\limits _{x\in {\mathbb {R}}^3} {\{\tfrac{1}{\delta }h(x{-}a)+\psi (x)\} }\). Then, \(\tfrac{1}{\delta }h(a_\delta {-}a) \le \psi _\delta ^{{\textrm{ic}}} \le \psi (a)\), so that \(\lim _{\delta \rightarrow 0^+}h(a_\delta {-}a) =0\), hence \(|a_\delta {-}a| = \sqrt{(h(a_\delta {-}a){+}1)^2{-}1} \longrightarrow 0\) as \(\delta \rightarrow 0^+\). All in all, we conclude that
\(\underline{\textit{Step 2. Smoothening}}\) We then define \(\psi ^\delta \in {\textrm{C}}^\infty ({\mathbb {R}}^3; {\mathbb {R}})\) via
Clearly, \(\psi ^\delta \) is also convex. Combining (8.31c) and (8.33a), (8.33b), and (8.33c) we gather that
Thus, \(\psi ^\delta \) has also linear growth. Taking into account that it is convex, from (8.35a) we easily deduce that
(where we have again used the notation \( |\partial \psi ^\circ (a)| = \inf \{ |\eta | : \eta \in \partial \psi (a)\})\). Finally,
The delamination system (8.4) featuring \(\widehat{\beta }^\delta \), \(\gamma ^\delta \), \(\widehat{\phi }^\delta \) and \(\psi ^\delta \) obviously has a gradient structure in the ambient spaces (8.6a), with the dissipation potentials from (8.6b) and (8.6c), and with the driving energy (cf. (8.17))
with \( {{\mathcal {E}}}_{{\textrm{elast}}}\) from (8.17), and


which indeed Mosco converges as \(\delta \rightarrow 0^+\), with respect to the topology of \({\textbf{U}}{\times }{\textbf{Z}}\), to the energy functional \({{\mathcal {E}}}\) from (8.6d). We will pass to the limit, as \(\delta \rightarrow 0^+\), in the corresponding energy-dissipation balance (4.18b) to prove that the solutions \((u^\varepsilon _\delta ,z^\varepsilon _\delta )_\delta \) to the regularized delamination system converge to a solution of the original system (8.4), satisfying the basic energy estimate (8.20) as well as the rate-independent a priori estimate (8.29).
Proposition 8.5
(Existence of viscous solutions with improved estimates) Under assumptions (8.5) for \(\widehat{\beta }\), \(\psi \), \(\gamma \), and \(\widehat{\phi }\) and the compatibility conditions (8.11) on the initial data \((u_0,z_0)\), there exists a constant \(C_*>0\) such that for all \(\varepsilon >0\) there exists a solution \((u_\varepsilon ,z_\varepsilon ) \in {\textrm{H}}^1(0,T;{\textbf{U}}){\times }{\textrm{H}}^1(0,T;{\textbf{Z}}_{{\textrm{e}}})\) satisfying the energy estimate (8.20) with \(C_1^{E_0}=C_*\), as well as the improved estimate

Proof
Let \((\delta _k)_k\) be a null sequence and, for \(\varepsilon >0\) fixed, let \((q^\varepsilon _{\delta _k})_k\) be the corresponding sequence of solutions to the regularized system (8.4); from now on, we will simply write \((q_k)_k\). Our starting point is the energy-dissipation balance
with
Relying on the energy estimate (8.20) and on well known compactness results, we infer that there exists \(q_\varepsilon = (u_\varepsilon ,z_\varepsilon ) \) such that, along a not relabeled subsequence,
It also follows from estimate (4.25a) in Lemma 4.12 that there exist \(\mu _\varepsilon \) and \(\zeta _\varepsilon \) such that, up to a further subsequence,
In order to identify the weak limit \(\zeta _\varepsilon (t)\) as an element of \(\partial _{\textsf{z}}{{\mathcal {E}}}(t,u_\varepsilon (t), z_\varepsilon (t))\) for almost all \(t\in (0,T)\), we observe that, by (8.31b), \(|(\gamma ^{{\delta _k}})'(z_k ) | \le \delta + |\partial \gamma ^o(z_k) | \le \delta +1\), taking into account that \(\gamma (z) = \max \{ z,0\}\). Therefore,
with (1) due to (8.35a) and (2) to (8.5). Since \((u_k)_k\) is bounded in \({\textrm{L}}^\infty (0,T;{\textrm{H}}^1(\Omega ;{\mathbb {R}}^3))\), we immediately deduce that \(((\gamma ^{{\delta _k}})'(z_k ) \psi ^\delta (\llbracket u_k \rrbracket ) )_k\) is bounded in \({\textrm{L}}^\infty (0,T;{\textrm{L}}^2(\Gamma _{{\textrm{C}}}))\). A standard argument based on the fact that \(z\mapsto \phi ^{\delta _k}(z)+\Lambda _\phi z\) is a non-decreasing function then yields a separate estimate in \({\textrm{L}}^2(0,T;{\textrm{L}}^2(\Gamma _{{\textrm{C}}}))\) for both \(({{\textbf { A}}}z_k)_k\) and \(( \phi ^{{\delta _k}}(z_k))_k\) so that, up to a subsequence, \(\phi ^{{\delta _k}}(z_k) \rightharpoonup \phi \) in \({\textrm{L}}^2(0,T;{\textrm{L}}^2(\Gamma _{{\textrm{C}}}))\) for some \(\phi \). Combining this with the fact that \(z_k\rightarrow z_\varepsilon \) in \({\textrm{L}}^2(0,T;{\textrm{L}}^2(\Gamma _{{\textrm{C}}}))\) we immediately conclude by (8.31d) that \(\phi \in \partial \widehat{\phi }(z_\varepsilon )\) a.e. in \((0,T){\times }\Gamma _{{\textrm{C}}}\). With the same arguments we find that \((\gamma ^{{\delta _k}})'(z_k )\overset{*}{\rightharpoonup }\omega \) in \({\textrm{L}}^\infty ((0,T){\times }\Gamma _{{\textrm{C}}})\) with \(\omega \in \partial \gamma (z_\varepsilon )\) a.e. in \((0,T){\times }\Gamma _{{\textrm{C}}}\). Finally, again applying (8.35a) to estimate \(| \psi ^\delta (\llbracket u_k \rrbracket )| \) and taking into account that \(\llbracket u_k \rrbracket \rightarrow \llbracket u \rrbracket \) strongly in \({\textrm{L}}^\infty (0,T;{\textrm{L}}^q(\Gamma _{{\textrm{C}}}))\) for every \(1\le q<4\), with the dominated convergence theorem we conclude that \(\psi ^\delta (\llbracket u_k \rrbracket )\rightarrow \psi (\llbracket u_\varepsilon \rrbracket )\), for instance, in \({\textrm{L}}^{3/2}((0,T){\times }\Gamma _{{\textrm{C}}})\). All in all, we find that \((\gamma ^{{\delta _k}})'(z_k ) \psi ^\delta (\llbracket u_k \rrbracket ) \rightharpoonup \omega \psi (\llbracket u_\varepsilon \rrbracket )\) in \({\textrm{L}}^{3/2}((0,T){\times }\Gamma _{{\textrm{C}}})\). We have thus proved that
and thus \(\zeta _\varepsilon (t) \in \partial _{\textsf{z}}{{\mathcal {E}}}(t,u_\varepsilon (t), z_\varepsilon (t))\).
The identification of \(\mu _\varepsilon \) as an element of \(\partial _{\textsf{u}}{{\mathcal {E}}}(\cdot ,u_\varepsilon (\cdot ), z_\varepsilon (\cdot ))\) first of all follows from observing that, by (8.39), \( {{\textbf { C}}}u_k \overset{*}{\rightharpoonup }{{\textbf { C}}}u\) in \({\textrm{L}}^\infty (0,T;{\textbf{U}}^*)\). Moreover, with similar arguments as in the above lines, based on properties (8.31), we find that \(\gamma ^{{\delta _k}}(z_k) \rightarrow \gamma (z_\varepsilon )\) in \({\textrm{L}}^q((0,T){\times }\Gamma _{{\textrm{C}}})\) for all \(1\le q<\infty \) and, recalling that \(\beta \) is Lipschitz, that there exists \({\widetilde{\beta }} \in {\textrm{L}}^\infty (0,T;{\textrm{L}}^4(\Gamma _{{\textrm{C}}}))\) such that \(\beta ^{\delta _k}(\llbracket u_k \rrbracket ) \rightharpoonup \widetilde{\beta }\) in \( {\textrm{L}}^\infty (0,T;{\textrm{L}}^4(\Gamma _{{\textrm{C}}}))\). Finally, taking into account (8.35b) and the fact that \(\psi \) has quadratic growth we conclude that there exists \(\varrho \in {\textrm{L}}^\infty (0,T;{\textrm{L}}^4(\Gamma _{{\textrm{C}}}))\) such that \({\textrm{D}}\psi ^{\delta _k}(\llbracket u_k \rrbracket ) \overset{*}{\rightharpoonup }\varrho \) in \({\textrm{L}}^\infty (0,T;{\textrm{L}}^4(\Gamma _{{\textrm{C}}}))\). All in all, we find that
and it remains to show that \(\eta = {\varvec{J}}^*(\beta (\llbracket u \rrbracket )+\gamma (z) {\textrm{D}}\psi (\llbracket u \rrbracket ) )\). For this, we observe that the functionals \({\mathcal {J}}^{\delta _k}: {\textrm{L}}^2(0,T; {\textbf{U}}{{\times }}{\textbf{Z}}) \rightarrow {\mathbb {R}}\) defined by \( {\mathcal {J}}^{\delta _k} (u,z): = \int _0^T \mathcal {}\int _{\Gamma _{{\textrm{C}}}} \big (\widehat{\beta }^{\delta _k}(\llbracket u \rrbracket )+\gamma ^{\delta _k}(z) \psi ^{\delta _k}(\llbracket u \rrbracket )\big ) \,\,\!{\textrm{d}}x \,\,\!{\textrm{d}}t, \) clearly fulfilling
enjoy the following property:
Hence, we need to prove that
This follows from testing the u-equation (8.4a) at the level \(\delta _k\) by \(u_k\), taking the limit as \(k\rightarrow \infty \), and using that, by the convergence arguments in the above lines, the quadruple \((u,z,{{\tilde{\beta }}},\varrho )\) fulfills the limit equation \( 0 = \varepsilon ^\alpha {{\textbf { D}}}\dot{u}_\varepsilon + {{\textbf { C}}}u_\varepsilon + +{\varvec{J}}^*({{\tilde{\beta }}}{+}\gamma (z_\varepsilon ) \varrho ) - \ell _u \) in \({\textbf{U}}^*\) a.e. in (0, T). All in all, we conclude that \( {\varvec{J}}^*({{\tilde{\beta }}} {+} \gamma (z_\varepsilon ) \varrho )\) \(\in {\varvec{J}}^*(\beta (z_\varepsilon ){+} \gamma (z_\varepsilon ) \partial \psi (\llbracket u_\varepsilon \rrbracket ))\), so that
Therefore, passing to the limit as \(k\rightarrow \infty \) in (4.18b) we infer that the quadruple \((u_\varepsilon ,z_\varepsilon , \mu _\varepsilon , \zeta _\varepsilon )\) fulfills \(( \mu _\varepsilon (t), \zeta _\varepsilon (t)) \in \partial _{\textsf{q}}{{\mathcal {E}}}(t,q_\varepsilon (t))\) for almost all \(t\in (0,T)\), joint with the energy-dissipation upper estimate in (4.18b). Now, by Proposition 8.2 the energy functional \({{\mathcal {E}}}\) from (8.6d) complies with the chain rule of Hypothesis 4.7. Hence, by Remark 4.9 the validity of the energy-dissipation upper estimate is sufficient to conclude that \((u_\varepsilon ,z_\varepsilon )\) solve the Cauchy problem for the delamination system (8.4).
By lower semicontinuity arguments, the a priori estimate (8.29) is inherited by \((u_\varepsilon ,z_\varepsilon )\). This concludes the proof of Proposition 8.5 and, ultimately, of Theorem 8.1. \(\square \)
Data Availability Statement
Data sharing is not applicable to this article as no data sets were generated or analyzed during the current study.
References
Alessi, R., Crismale, V., Orlando, G.: Fatigue effects in elastic materials with variational damage models: a vanishing viscosity approach. J. Nonlinear Sci. 29(3), 1041–1094, 2019
Ambrosio, L.: Minimizing movements. Rend. Accad. Naz. Sci. XL Mem. Mat. Appl. (5) 19, 1773–1799, 1995
Ambrosio, L., Gigli, N., Savaré, G.: Gradient Flows in Metric Spaces and in the Space of Probability Measures, 2nd edn. Lectures in Mathematics ETH Zürich. Birkhäuser Verlag, Basel (2008)
Babadjian, J.-F., Francfort, G., Mora, M.: Quasistatic evolution in non-associative plasticity—the cap model. SIAM J. Math. Anal. 44, 245–292, 2012
Bacho, A.: On the nonsmooth analysis of doubly nonlinear evolution inclusions of first and second order with applications, Ph.D. thesis, Technische Universität Berlin (2021). https://doi.org/10.14279/depositonce-12327
Bogachev, V.I.: Measure Theory, vol. I, II. Springer-Verlag, Berlin (2007)
Brézis, H.: Opérateurs maximaux monotones et semi-groupes de contractions dans les espaces de Hilbert. North-Holland Publishing Co., Amsterdam (1973)
Castaing, C., Valadier, M.: Convex analysis and measurable multifunctions, vol. 580. Lectures Notes in Mathematics. Springer, Berlin (1977)
Crismale, V., Lazzaroni, G.: Viscous approximation of quasistatic evolutions for a coupled elastoplastic-damage model. Calc. Var. Partial Differ. Equ. 55(1), 17, 54, 2016
Crismale, V., Rossi, R.: Balanced viscosity solutions to a rate-independent coupled elasto-plastic damage system. SIAM J. Math. Anal. 53(3), 3420–3492, 2021
Dal Maso, G., Scala, R.: Quasistatic evolution in perfect plasticity as limit of dynamic processes. J. Dyn. Differ. Equ. 26, 915–954, 2014
Dal Maso, G., Toader, R.: A model for the quasi-static growth of brittle fractures: existence and approximation results. Arch. Ration. Mech. Anal. 162(2), 101–135, 2002
Dal Maso, G., DeSimone, A., Solombrino, F.: Quasistatic evolution for cam-clay plasticity: a weak formulation via viscoplastic regularization and time rescaling. Calc. Var. Partial Differ. Equ. 40, 125–181, 2011
Efendiev, M., Mielke, A.: On the rate-independent limit of systems with dry friction and small viscosity. J. Convex Anal. 13(1), 151–167, 2006
Francfort, G.A., Marigo, J.-J.: Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 46(8), 1319–1342, 1998
Francfort, G., Stefanelli, U.: Quasistatic evolution for the Armstrong–Frederick hardening-plasticity model. Appl. Math. Res. Express 2, 297–344, 2013
Gilardi, G., Rocca, E.: Convergence of phase field to phase relaxation models governed by an entropy equation with memory. Math. Methods Appl. Sci. 29(18), 2149–2179, 2006
Halphen, B., Nguyen, Q.: Sur les matériaux standards généralisés. J. Mécanique 14, 39–63, 1975
Ioffe, A.D.: On lower semicontinuity of integral functionals. I. SIAM J. Control Optim. 15(4), 521–538, 1977
Knees, D., Negri, M.: Convergence of alternate minimization schemes for phase-field fracture and damage. Math. Models Methods Appl. Sci. 27(9), 1743–1794, 2017
Knees, D., Zanini, C.: Existence of parameterized \(BV\)-solutions for rate-independent systems with discontinuous loads. Discr. Contin. Dyn. Syst. Ser. S 14(1), 121–149, 2021
Knees, D., Mielke, A., Zanini, C.: On the inviscid limit of a model for crack propagation. Math. Models Methods Appl. Sci. 18(9), 1529–1569, 2008
Knees, D., Rossi, R., Zanini, C.: A vanishing viscosity approach to a rate-independent damage model. Math. Models Methods Appl. Sci. 23(4), 565–616, 2013
Knees, D., Rossi, R., Zanini, C.: Balanced viscosity solutions to a rate-independent system for damage. Eur. J. Appl. Math. 30(1), 117–175, 2019
Kočvara, M., Mielke, A., Roubíček, T.: A rate-independent approach to the delamination problem. Math. Mech. Solids 11, 423–447, 2006
Lazzaroni, G., Toader, R.: A model for crack propagation based on viscous approximation. Math. Models Methods Appl. Sci. 21(10), 2019–2047, 2011
Liero, M., Mielke, A., Savaré, G.: Optimal entropy-transport problems and a new Hellinger–Kantorovich distance between positive measures. Invent. Math. 211, 969–1117, 2018
Maggiani, G.B., Mora, M.G.: A dynamic evolution model for perfectly plastic plates. Math. Models Methods Appl. Sci. 26(10), 1825–1864, 2016
Mielke, A.: Evolution in rate-independent systems (Ch.6). In: Dafermos, C., Feireisl, E. (eds.) Handbook of Differential Equations, Evolutionary Equations, vol. 2, pp. 461–559. Elsevier B.V, Amsterdam (2005)
Mielke, A.: Differential, energetic, and metric formulations for rate-independent processes. In: Ambrosio, L., Savaré, G. (eds.) Nonlinear PDE’s and Applications, vol. 2028, pp. 87–170. Lect. Notes Math. Springer (C.I.M.E. Summer School, Cetraro, Italy 2008), Berlin (2011)
Mielke, A.: On evolutionary \(\Gamma \)-convergence for gradient systems (Ch. 3). In: Muntean, A., Rademacher, J., Zagaris, A. (eds.) Macroscopic and Large Scale Phenomena: Coarse Graining, Mean Field Limits and Ergodicity, vol. 3, pp. 187–249. Lecture Notes in Applied Math. Mechanics. Springer, Berlin (2016)
Mielke, A., Rossi, R.: On De Giorgi’s lemma for variational interpolants. In preparation (2023)
Mielke, A., Roubíček, T.: Rate-Independent Systems. Theory and Application, vol. 193. Applied Mathematical Sciences. Springer, New York (2015)
Mielke, A., Theil, F.: A mathematical model for rate-independent phase transformations with hysteresis. In: Alber, H.-D., Balean, R., Farwig, R. (eds.) Proceedings of the Workshop on “Models of Continuum Mechanics in Analysis and Engineering” (Aachen), pp. 117–129. Shaker-Verlag (1999)
Mielke, A., Theil, F.: On rate-independent hysteresis models. NoDEA Nonlinear Differ. Equ. Appl. 11(2), 151–189, 2004
Mielke, A., Zelik, S.: On the vanishing-viscosity limit in parabolic systems with rate-independent dissipation terms. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 13(1), 67–135, 2014
Mielke, A., Theil, F., Levitas, V.I.: A variational formulation of rate-independent phase transformations using an extremum principle. Arch. Ration. Mech. Anal. 162(2), 137–177, 2002
Mielke, A., Rossi, R., Savaré, G.: Modeling solutions with jumps for rate-independent systems on metric spaces. Discr. Contin. Dyn. Syst. Ser. A 25(2), 585–615, 2009
Mielke, A., Rossi, R., Savaré, G.: BV solutions and viscosity approximations of rate-independent systems. ESAIM Control Optim. Calc. Var. 18(1), 36–80, 2012
Mielke, A., Rossi, R., Savaré, G.: Variational convergence of gradient flows and rate-independent evolutions in metric spaces. Milan J. Math. 80(2), 381–410, 2012
Mielke, A., Rossi, R., Savaré, G.: Nonsmooth analysis of doubly nonlinear evolution equations. Calc. Var. Partial Differ. Equ. 46(1–2), 253–310, 2013
Mielke, A., Rossi, R., Savaré, G.: Balanced viscosity (BV) solutions to infinite-dimensional rate-independent systems. J. Eur. Math. Soc. (JEMS) 18(9), 2107–2165, 2016
Mielke, A., Rossi, R., Savaré, G.: Balanced-viscosity solutions for multi-rate systems. J. Phys. Conf. Ser. 727, 010210, 2016
Mielke, A., Rossi, R., Stephan, A.: On time-splitting methods for gradient flows with two dissipation mechanisms. In preparation (2023)
Negri, M.: Quasi-static rate-independent evolutions: characterization, existence, approximation and application to fracture mechanics. ESAIM Control Optim. Calc. Var. 20(4), 983–1008, 2014
Racca, S.: A viscosity-driven crack evolution. Adv. Calc. Var. 5(4), 433–483, 2012
Rindler, F., Schwarzacher, S., Velázquez, J.L.: Two-speed solutions to non-convex rate-independent systems. Arch. Ration. Mech. Anal. 239, 1667–1731, 2021
Rossi, R.: From visco to perfect plasticity in thermoviscoelastic materials. Z. Angew. Math. Mech. 98(7), 1123–1189, 2018
Rossi, R., Thomas, M.: From an adhesive to a brittle delamination model in thermo-visco-elasticity. ESAIM Control Optim. Calc. Var. 21, 1–59, 2015
Rossi, R., Thomas, M.: Coupling rate-independent and rate-dependent processes: existence results. SIAM J. Math. Anal. 49(2), 1419–1494, 2017
Rossi, R., Mielke, A., Savaré, G.: A metric approach to a class of doubly nonlinear evolution equations and applications. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 7(1), 97–169, 2008
Roubíček, T.: Rate-independent processes in viscous solids at small strains. Math. Methods Appl. Sci. 32(7), 825–862, 2009
Roubíček, T.: Thermodynamics of rate-independent processes in viscous solids at small strains. SIAM J. Math. Anal. 42(1), 256–297, 2010
Roubíček, T.: Thermodynamics of perfect plasticity. Discr. Contin. Dyn. Syst. Ser. S 6(1), 193–214, 2013
Roubíček, T.: Adhesive contact of visco-elastic bodies and defect measures arising by vanishing viscosity. SIAM J. Math. Anal. 45(1), 101–126, 2013
Roubíček, T., Tomassetti, G.: Thermomechanics of damageable materials under diffusion: modelling and analysis. Z. Angew. Math. Phys. 66(6), 3535–3572, 2015
Roubíček, T., Scardia, L., Zanini, C.: Quasistatic delamination problem. Contin. Mech. Thermodyn. 21(3), 223–235, 2009
Scala, R.: Limit of viscous dynamic processes in delamination as the viscosity and inertia vanish. ESAIM Control Optim. Calc. Var. 23(2), 593–625, 2017
Stefanelli, U., Wachsmuth, D., Wachsmuth, G.: Optimal control of a rate-independent evolution equation via viscous regularization. Discr. Contin. Dyn. Syst. Ser. S 10(6), 1467–1485, 2017
Valadier, M.: Young measures. In: Methods of Nonconvex Analysis. CIME Lectures held in Varenna 1989. Springer Lect. Notes Math., vol. 1446, pp. 152–188. Springer, Berlin (1990)
Acknowledgements
A.M. was partially supported by Deutsche Forschungsgemeinschaft (DFG) via the Priority Program SPP 2256 “Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials” (project No. 441470105), subproject Mi 459/9-1 Analysis for thermo-mechanical models with internal variables. The authors are grateful to Giuseppe Savaré for helpful and stimulating discussions. The authors are also indebted to an anonymous referee for very carefully reading the paper, as well as for several constructive and insightful suggestions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by G. Dal Maso.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Alexander Mielke was partially supported by DFG within SPP 2256 (No. 441470105) under Grant Mi 459/9-1.
Appendices
Appendix A: Chain Rules
In this section we first of all provide a sufficient condition for the chain-rule Hypothesis 4.7 (and, in fact, for the closedness Hypothesis 4.5 as well). More precisely, we will show that its validity is guaranteed by a sort of uniform subdifferentiability property of the energy \({{\mathcal {E}}}\) on its sublevels, cf. (A.1) below, which we borrow from [41]; as already observed in the proof of Proposition 8.2, (A.1) for instance holds for \(\lambda \)-convex functionals. The proof of the following result combines the argument for [41, Prop. 2.4] with results from [3].
Proposition A.1
Let \({{\mathcal {E}}}: [0,T]\times {\textbf{Q}} \rightarrow (-\infty , +\infty ] \) comply with Hypothesis 4.3. Assume that for every \(E>0\) there exists a modulus of subdifferentiability \(\varpi ^E: [0,T]{\times }{\mathcal {S}}_{E} {\times }{\mathcal {S}}_{E} \rightarrow [0,\infty )\) such that for all \(t\in [0,T]:\)

Then, \({{\mathcal {E}}}\) complies with Hypothesis 4.7.
Proof
In order to show Hypothesis 4.7, let \(q\in {\textrm{AC}}([0,T];{\textbf{Q}})\) and \(\xi \in {\textrm{L}}^1(0,T;{\textbf{Q}}^*)\) fulfill (4.15), and let \(E>0\) be such that \(q(t) \in {\mathcal {S}}_{E}\) for all \(t\in [0,T]\). Preliminarily, let us suppose that \({{\mathcal {E}}}\) is independent of time, i.e. \({{\mathcal {E}}}(t,q) = {\overline{{{\mathcal {E}}}}}(q)\) (with a modulus of subdifferentiability \(\varpi ^E (t,\cdot ,\cdot ) = \varpi ^E(\cdot ,\cdot )\)), and let us prove the absolute continuity of \([0,T] \ni t \mapsto {\overline{{{\mathcal {E}}}}}(q(t))\). For this, as in [41] we resort to [3, Lemma 1.1.4] and reparametrize q to a 1-Lipschitz curve \({{\tilde{q}}}: [0,L]\rightarrow {\textbf{Q}}\), with \(L = \int _0^T \Vert q'(t)\Vert _{{\textbf{Q}}} \,\,\!{\textrm{d}}t\), \({{\tilde{q}}}: = q \circ {{\tilde{t}}}\), and \({{\tilde{t}}}: [0,L]\rightarrow [0,T]\) the left-continuous, increasing map
Let us set \({{\tilde{\xi }}}(s):= \xi ({{\tilde{t}}}(s))\). Then, it follows from (4.15) and a version of the change of variables formula (cf., e.g., [6, Thm. 5.8.30]), that
whence \({{\tilde{\xi }}} \in {\textrm{L}}^1(0,L)\). Hence, we are in a position to repeat the very same arguments from the proof of [41, Prop. 2.4]. Namely, relying on the validity of (A.1) we obtain that

for all \(0\le s_1\le s_2 \le L\). Exchanging the role of \(s_1\) and \(s_2\) and exploiting the 1-Lipschitz continuity of \({{\tilde{q}}}\) leads to
From the above estimate the absolute continuity of the function \([0,L]\ni s\mapsto {\overline{{{\mathcal {E}}}}} ({\tilde{q}}(s))\) follows by repeating the very same arguments as in the proof of [3, Thm. 1.2.5]. Again changing variables in the integral we infer that \([0,T]\ni t \mapsto {\overline{{{\mathcal {E}}}}}(q(t))\) is absolutely continuous.
In the general case, let us first of all check the absolute continuity of \([0,T]\ni t \mapsto {\mathcal {E}}(t,q(t))\), namely that for every \(\varepsilon >0\) there exists \(\delta >0\) such that for every collection of pairwise disjoint intervals \((a_i,b_i) \subset (0,T)\), \(i=1,\ldots , M\), there holds
In order to obtain the above estimate, we use that
and estimate the first term via (4.7d), so that
Hence, we choose \(\delta _1 =\frac{\varepsilon }{2C_1E}\) and get \(\sum _{i=1}^{M}|{\mathcal {E}}(b_i,q(b_i)){-} {\mathcal {E}}(a_i,q(a_i))|<\tfrac{\varepsilon }{2} \). As for the second term in (A.3), we rely on the absolute continuity of \({\overline{{{\mathcal {E}}}}}(q): = {\mathcal {E}}(a_i,q)\). We thus conclude (A.2). Finally, to show the chain-rule formula (4.16), we fix a point \(t\in (0,T)\) in which \(q'(t)\) and \(\frac{{\textrm{d}}}{{\textrm{d}}t}{\mathcal {E}}(t,q(t))\) exist, and derive from (A.1) that

We now divide the above estimate by \(h>0\) and take the limit as \(h\rightarrow 0^+\). Now, recall that \(q(t) \in {\mathcal {S}}_{E}\) for all \(t\in [0,T]\). Therefore, thanks to Hypothesis 4.5 the function \([0,T]{\times }[0,T]\ni (r,s) \mapsto \partial _t {\mathcal {E}}(r,q(s))\) is uniformly continuous, with a modulus of continuity \(\omega : [0,T]\times [0,T]\rightarrow [0,\infty )\), so that
Taking into account that \(\lim _{h\rightarrow 0^+ } \tfrac{1}{h} \int _t^{t+h} \partial _t {\mathcal {E}}(r,q(r)) \,\,\!{\textrm{d}}r = \partial _t {\mathcal {E}}(t,q(t))\), (A.4) thus leads to the estimate \(\ge \) in (4.16). The converse inequality follows by dividing (A.4) by \(h<0\) and taking the limit as \(h \rightarrow 0^-\). This concludes the proof. \(\square \)
Let us now carry out the proof of Proposition 5.17, which shows the validity of the parametrized chain rule from Hypothesis 5.8 if Hypothesis 4.7 holds and, in addition, the vanishing-viscosity contact potentials associated with \({{\mathcal {V}}}_{\textsf{u}}\) and \({{\mathcal {V}}}_{\textsf{z}}\) satisfy the coercivity property (5.39).
Proof of Proposition 5.17
Preliminarily, we observe that, if the vanishing-viscosity contact potentials \({\mathfrak {b}}_{{{\mathcal {V}}}_{\textsf{u}}}\) and \({\mathfrak {b}}_{{{\mathcal {V}}}_{\textsf{z}}}\) satisfy (5.39), then the ‘reduced’ rescaled joint M-function \({\mathfrak {M}}_{0}^{\alpha ,{\textrm{red}}}\) enjoys the following coercivity property:
Clearly, the above estimate trivially holds if \(t'>0\), as then \({\mathscr {S}}_{\textsf{u}}^*(t,q) = {\mathscr {S}}_{\textsf{z}}^*(t,q)=0\), so that \( {\mathfrak {A}}_{\textsf{u}}^{*}(t,q)= \{0\}\) and every \( \zeta \in {\mathfrak {A}}_{\textsf{z}}^{*}(t,q)\) fulfills \(-\zeta \in \partial {{\mathcal {R}}}(0)\). To show it for \(t'=0\), we will separately discuss the cases \(\alpha >1\) (the arguments for \(\alpha \in (0,1)\) are indeed specular) and \(\alpha =1\). In the case \(\alpha >1\), we have that, if \({\mathscr {S}}_{\textsf{u}}^*(t,q)=0\), then by (5.12) we have
for all \( \zeta \in {\mathfrak {A}}_{\textsf{z}}^{*}(t,q)\) and all \(\sigma \in \partial {{\mathcal {R}}}(0)\) with \( {\mathcal {W}}_{\textsf{z}}^*(\zeta ) = {{\mathcal {V}}}_{\textsf{z}}^*(\zeta {-}\sigma )\), where (1) follows from (5.39). Analogously, if \({\mathscr {S}}_{\textsf{u}}^*(t,q)>0\), then \({\mathfrak {M}}_{0}^{\alpha ,{\textrm{red}}}(t,q, t',q') = {\mathfrak {b}}_{{{\mathcal {V}}}_{\textsf{u}}} (u',{\mathscr {S}}_{\textsf{u}}^*(t,q)) \) and we have the analogous estimate. If \(\alpha =1\), then by (5.12) and again (3.9) we have
for all \( \mu \), \(\zeta \), and \(\sigma \) as in (A.5).
Let us now consider an admissible curve \( ({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}} ([a,b];[0,T]{\times }{\textbf{Q}})\) such that, in addition, \({\textsf{z}}\in {\textrm{AC}}([a,b];{\textbf{Z}})\). Hence, \({\mathfrak {M}}_0^\alpha [{\textsf{t}},{\textsf{q}},{\textsf{t}}',{\textsf{q}}'] = {\mathfrak {M}}_0^\alpha ({\textsf{t}},{\textsf{q}},{\textsf{t}}',{\textsf{q}}') \) a.e. in (a, b). Then, (5.21) yields that \( {\mathfrak {M}}_0^\alpha ({\textsf{t}},{\textsf{q}},{\textsf{t}}',{\textsf{q}}') \in {\textrm{L}}^1(a,b)\). Let us now choose measurable selections \((a,b) \ni s \mapsto \mu (s) \in {\mathfrak {A}}_{\textsf{u}}^{*}({\textsf{t}}(s),{\textsf{q}}(s)) \), \((a,b) \ni s \mapsto \zeta (s) \in {\mathfrak {A}}_{\textsf{z}}^{*}({\textsf{t}}(s),{\textsf{q}}(s)) \), and \((a,b) \ni s \mapsto \sigma (s) \in \partial {{\mathcal {R}}}(0)\) such that
Hence, we have \( \int _a^b \left( \Vert \mu (s) \Vert _{{\textbf{U}}^*} \Vert {\textsf{u}}'(s)\Vert _{\textbf{U}}{+} \Vert \zeta (s) {+}\sigma (s)\Vert _{{\textbf{Z}}^*} \Vert {\textsf{z}}'(s)\Vert _{\textbf{Z}}\right) \,\,\!{\textrm{d}}s <\infty \), and using \(\int _a^b \Vert \sigma (s)\Vert _{{\textbf{Z}}^*} \Vert {\textsf{z}}'(s)\Vert _{\textbf{Z}}\,\,\!{\textrm{d}}s \) \(\le C_{{\mathcal {R}}}\int _a^b \Vert {\textsf{z}}'(s)\Vert _{\textbf{Z}}\,\,\!{\textrm{d}}s <\infty \) by (4.6), we ultimately deduce that
We are thus in a position to apply the chain rule from Hypothesis 4.7 and conclude that \(s\mapsto {\mathcal {E}}({\textsf{t}}(s),{\textsf{q}}(s))\) is absolutely continuous and that

Then, the chain-rule estimate (5.40) follows from observing that the right-hand side in the above formula estimates \(- {\mathfrak {M}}_0^\alpha ({\textsf{t}},{\textsf{q}},{\textsf{t}}',{\textsf{q}}') \) from above thanks to Lemma 5.5. This concludes the proof. \(\square \)
We conclude this section with a result relating parametrized chain rule from Hypothesis 5.8 to that in Hypothesis 6.4.
Lemma A.2
If the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\) satisfies the chain rule of Hypothesis 5.8, then it also satisfies Hypothesis 6.4.
Proof
Consider a curve \(q \in {\textrm{BV}}([0,T];{\textbf{U}}) {\times }({\textrm{R}}([0,T];{\textbf{Z}}) {\cap } \textrm{BV}([0,T];{\textbf{Z}}_{{\textrm{ri}}}) )\) fulfilling the stationary equation (6.10a) and the local stability (6.10b), and let us fix \([t_0,t_1] \subset [0,T]\). As in Theorem 6.15(2), we associate with q a parametrized curve \(({\textsf{t}},{\textsf{q}}) = ({\textsf{t}},{\textsf{u}},{\textsf{z}}) \in {\mathscr {A}} ([{{{\textsf{S}}}}_0,{{{\textsf{S}}}}_1]; [t_0,t_1]{\times }{\textbf{Q}})\) such that (6.27) holds on the interval \([t_0,t_1]\). The parametrized chain-rule inequality (5.24) reads for a.a. \(s\in ({{{\textsf{S}}}}_0,{{{\textsf{S}}}}_1) \)
Integrating on the interval \( ({{{\textsf{S}}}}_0,{{{\textsf{S}}}}_1)\) and using (6.27), we conclude the desired chain-rule inequality (6.9). With this, Lemma A.2 is proved. \(\square \)
Appendix B: Measurability in Theorem 5.21
To prove the statement in Theorem 5.21 concerning the existence of measurable selections \( \xi =(\mu ,\zeta ): (0,{{{\textsf{S}}}}) \rightarrow {\textbf{U}}^* {\times }{\textbf{Z}}^*\) and \((\lambda _{\textsf{u}},\lambda _{\textsf{z}}): (0,{{{\textsf{S}}}})\rightarrow [0,\infty ]^2 \) satisfying (5.49), we will resort to the following generalization of Filippov’s Selection Theorem, proved in [33, Prop. B.1.2].
Proposition B.1
Let \((O,{\mathfrak {O}}, \mu )\) be a \(\sigma \)-finite complete measure space and X a complete separable metric space. Let \(F: O \rightrightarrows X\) be a measurable set-valued mapping with closed non-empty images, \({{let\,\,graph}}(F): = \{ (s,x):x \in F(s)\} \) be its graph, and let \({\mathfrak {G}}\) be the \(\sigma \)-algebra given by the restriction of \({\mathfrak {O}}\times {\mathfrak {B}}(X)\) (with \({\mathfrak {B}}(X)\) the Borel \(\sigma \)-algebra on X) to \({\textrm{graph}}(F)\). Let \(g: {\textrm{graph}}(F) \rightarrow {\mathbb {R}}\) be a \({\mathfrak {G}}\)-measurable mapping such that
Then, there exists a measurable selection \(f: O \rightarrow X \) of F such that \( g(s,f(s)) =0 \) for all \(s\in O\).
For the construction of the parameters \(\lambda _{\textsf{u}}\) and \(\lambda _{\textsf{z}}\) introduce the sets \(\Lambda _{\textsf{x}}(v,\sigma )\) via
with \({\textsf{x}} \in \{{\textsf{u}},{\textsf{z}}\}\) and \( {\textbf{X}} \in \{{\textbf{U}}, {\textbf{Z}}\}\). Recall that Proposition 3.2 guarantees that \(\Lambda _{\textsf{x}}(v,\sigma ) \ne \varnothing \) for all \(\sigma >0\). Analogously, for \(q'=(u',z')\) we will use the notation
A close perusal of the proof of Proposition 5.19 then reveals that, for a given \( (t,q,t',q') \in \Sigma _\alpha \) with \(\alpha \ne 1\),
for \( {\textsf{x}}\in \{ {\textsf{u}}, {\textsf{z}}\}\) and \( x' \in \{ u', z'\} \). Analogously, in the case \(\alpha =1\), we have that \((t,q,t',q') \in \Sigma _1 \cap {\textrm{V}}_{\textsf{uz}}\) if and only if (5.44) holds with \(\lambda \in \Lambda _{\textsf{uz}}(q',{\mathscr {S}}_{\textsf{u}}^*(t,q){+} {\mathscr {S}}_{\textsf{z}}^*(t,q)) \).
We are now in a position to the missing part of the proof of Theorem 5.21.
Proof of Part (1) of Theorem 5.21
Let \(({\textsf{t}},{\textsf{q}}) \in {\mathscr {A}}([0,{{{\textsf{S}}}}];[0,T]{\times }{\textbf{Q}})\) be an enhanced \(\text {pBV}\) solution of the rate-independent system \(({\textbf{U}}{\times } {\textbf{Z}},{{\mathcal {E}}},{{\mathcal {V}}}_{{\textsf{u}}}^{\varepsilon ^\alpha } \!{+}{{\mathcal {R}}}{+}{{\mathcal {V}}}_{{\textsf{z}}}^{\varepsilon })_{\varepsilon \downarrow 0}\). We will now prove the existence of measurable \(\lambda _{\textsf{u}},\, \lambda _{\textsf{z}}: (0,{{{\textsf{S}}}})\rightarrow [0,\infty ] \), and \( \mu : (0,{{{\textsf{S}}}}) \rightarrow {\textbf{U}}^*\) and \(\zeta : (0,{{{\textsf{S}}}}) \rightarrow {\textbf{Z}}^*\) satisfying (5.49) in the case \(\alpha >1\); with similar arguments one can obtain the analogous statement for \(\alpha =1\) and \(\alpha \in (0,1)\). To avoid trivial situations, we also suppose that \(({\textsf{t}},{\textsf{q}})\) is non-degenerate.
\(\underline{\textit{Step 1: Existence of measurable }\lambda _{\textsf{u}},\lambda _{\textsf{z}}: (0,{{{\textsf{S}}}})\rightarrow [0,\infty ].}\) Proposition 5.18 shows that \(({\textsf{t}}(s),{\textsf{q}}(s),{\textsf{t}}'(s),{\textsf{q}}'(s)) \) belongs to the contact set \( \Sigma _\alpha \) for a.a. \(s\in (0,{{{\textsf{S}}}})\) and that, in turn, \(\Sigma _\alpha \subset {\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}} \cup {\textrm{E}}_{\textsf{u}} {\textrm{V}}_{\textsf{z}} \cup {\textrm{B}}_{\textsf{z}}\). Recalling the short-hand notation (5.51), we introduce the short-hand \(((0,{{{\textsf{S}}}}) \cap {\textrm{B}}_{\textsf{z}})^\circ \) for the set \(\{({\textsf{t}},{\textsf{q}},{\textsf{t}}',{\textsf{q}}') \in {\textrm{B}}_{\textsf{z}} \text { and } {\mathscr {S}}_{\textsf{u}}^*({\textsf{t}},{\textsf{q}}) >0\}\). Since for \(\alpha >1\) we have \({\textsf{t}}'\equiv 0\) and \({\textsf{z}}'\equiv 0\) on \(((0,{{{\textsf{S}}}}) \cap {\textrm{B}}_{\textsf{z}})^\circ \) and since \(({\textsf{t}},{\textsf{q}})\) is non-degenerate, we have \({\textsf{u}}' \ne 0\) on \(((0,{{{\textsf{S}}}}) \cap {\textrm{B}}_{\textsf{z}})^\circ \). Therefore, thanks to Proposition 3.2, the set \( \Lambda _{\textsf{u}}({\textsf{u}}'(s),{\mathscr {S}}_{\textsf{u}}^*({\textsf{t}}(s),{\textsf{q}}(s))) = \mathop {{\textrm{Argmin}}}_{\lambda >0} {{\mathcal {B}}_{{{\mathcal {V}}}_{\textsf{u}}}\left( \tfrac{1}{\lambda },{\textsf{u}}'(s),{\mathscr {S}}_{\textsf{u}}^*({\textsf{t}}(s),{\textsf{q}}(s))\right) } \) is non-empty for every \(s\in ((0,{{{\textsf{S}}}}) \cap {\textrm{B}}_{\textsf{z}})^\circ \). We consider the multi-valued mapping \(\Gamma _{\textsf{u}}: ((0,{{{\textsf{S}}}}) \cap {\textrm{B}}_{\textsf{z}})^\circ \rightrightarrows [0,\infty )\) defined by \(\Gamma _{\textsf{u}}(s): = \Lambda _{\textsf{u}}({\textsf{u}}'(s),{\mathscr {S}}_{\textsf{u}}^*({\textsf{t}}(s),{\textsf{q}}(s)))\) and observe that its graph is a Borel subset of \((0,\infty )^2\). Indeed, \(\Gamma _{\textsf{u}}\) is given by the composition of the upper semicontinuous multi-valued mapping \(\Lambda _{{\textsf{u}}}\), with the Borel function \({\textsf{u}}'\) and the lower semicontinuous function \({\mathscr {S}}_{\textsf{u}}^*({\textsf{t}},{\textsf{q}})\).
Hence, we are in a position to apply the von Neumann-Aumann selection theorem (cf. [8, Thm. III.22]) to \(\Gamma _{\textsf{u}}\) and conclude that
Let N be the negligible subset of \((0,{{{\textsf{S}}}})\) on which either \({\textsf{t}}'\) or \({\textsf{q}}'\) do not exist, or \(({\textsf{t}},{\textsf{q}},{\textsf{t}}',{\textsf{q}}') \notin \Sigma _\alpha \): since \(\Sigma _\alpha \subset {\textrm{E}}_{\textsf{u}} {\textrm{R}}_{\textsf{z}} \cup {\textrm{E}}_{\textsf{u}} {\textrm{V}}_{\textsf{z}} \cup {\textrm{B}}_{\textsf{z}}\), we have that

Hence, we define \(\lambda _{\textsf{u}}\) on \((0,{{{\textsf{S}}}}){{\setminus }} N\) by
Analogously, we define \(\lambda _{\textsf{z}}\) on \((0,{{{\textsf{S}}}}) {{\setminus }} N\) by
Here, \(\widetilde{\lambda }_{{\textsf{z}}}: (0,{{{\textsf{S}}}})\cap {\textrm{E}}_{\textsf{u}}{\textrm{V}}_{\textsf{z}} \rightarrow (0,+\infty )\) is a measurable selection with \(\widetilde{\lambda }_{{\textsf{z}}}(s) \text {~lying in}\Lambda _{\textsf{z}}({\textsf{z}}'(s),{\mathscr {S}}_{\textsf{z}}^*({\textsf{t}}(s),{\textsf{q}}(s)))\), whose existence is again guaranteed by [8, Thm. III.22].
Clearly, \(\lambda _{\textsf{u}}\) and \(\lambda _{\textsf{z}}\) satisfy the switching conditions (5.49c). Also taking into account (B.2), we conclude that \(({\textsf{t}},{\textsf{q}})\) solve the subdifferential system (5.48) with \(\lambda _{\textsf{u}}\) and \(\lambda _{\textsf{z}}\).
\(\underline{\textit{Step 2: existence of measurable } \xi =(\mu ,\zeta ): (0,{{{\textsf{S}}}}) \rightarrow {\textbf{U}}^* {\times }{\textbf{Z}}^*.}\) We aim to apply Filippov’s theorem, in the form of Proposition B.1, with \(O = (0,{{{\textsf{S}}}}){{\setminus }} N\), \(X = {\textbf{U}}^* {\times }{\textbf{Z}}^*\), and the multi-valued mapping
Observe that F is measurable, with (non-empty) closed images thanks to Hypothesis 4.5. We now consider the mapping \(g: {\textrm{graph}}(F) \rightarrow {\mathbb {R}}\) given by

It turns out that, also in view of the discussion developed in Step 1, g is measurable. Furthermore, for every \(s\in (0,{{{\textsf{S}}}})\) the functional \(g(s,\cdot ,\cdot )\) is continuous thanks to the continuity of \({{\mathcal {R}}}\) and \({{\mathcal {V}}}_{\textsf{x}}\) and \({{\mathcal {V}}}_{\textsf{x}}^*\), \({\textsf{x}}\in \{{\textsf{u}}, {\textsf{z}}\}\). Finally, the first of conditions (B.1) holds since, by Step 1, \(({\textsf{t}},{\textsf{q}})\) solve the subdifferential system (5.48) with \(\lambda _{\textsf{u}}\) and \(\lambda _{\textsf{z}}\), which exactly means that for every \(s\in (0,{{{\textsf{S}}}}) {{\setminus }} N\) there exist \((\mu _s, \zeta _s) \in \partial _{\textsf{q}}{{\mathcal {E}}}({\textsf{t}}(s),{\textsf{q}}(s)) \) such that \(g(s,\mu _s,\zeta _s) = 0\). Hence, we are in a position to apply Proposition B.1, thus concluding that there exists a measurable selection \((0,{{{\textsf{S}}}}) {{\setminus }} N \ni s\mapsto (\mu (s),\zeta (s)) \in F(s)\) such that \( g(s,\mu (s),\zeta (s))\equiv 0\,. \) This yields the desired selection as stated in (5.49a). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mielke, A., Rossi, R. Balanced-Viscosity Solutions to Infinite-Dimensional Multi-Rate Systems. Arch Rational Mech Anal 247, 53 (2023). https://doi.org/10.1007/s00205-023-01855-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00205-023-01855-y




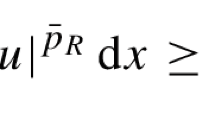

 for all
for all  for all
for all  such that
such that  for some
for some 