Skip to main content
SpringerLink
Log in

A new non-archimedean metric on persistent homology

  • Original paper
  • Published:
Computational Statistics Aims and scope Submit manuscript

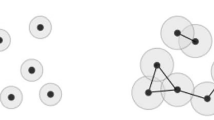
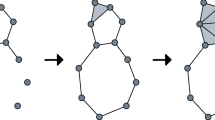
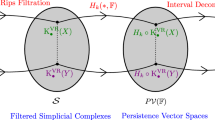
Abstract

In this article, we define a new non-archimedean metric structure, called cophenetic metric, on persistent homology classes of all degrees. We then show that zeroth persistent homology together with the cophenetic metric and hierarchical clustering algorithms with a number of different metrics do deliver statistically verifiable commensurate topological information based on experimental results we obtained on different datasets. We also observe that the resulting clusters coming from cophenetic distance do shine in terms of different evaluation measures such as silhouette score and the Rand index. Moreover, since the cophenetic metric is defined for all homology degrees, one can now display the inter-relations of persistent homology classes in all degrees via rooted trees.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Notes

  1. The source code and the data of the numerical experiments we conducted in the paper can be found on the authors’ GitHub page at https://github.com/ismailguzel/TDA-HC .

  2. The computational tools we use in this section are as follows: To compare dendrograms, we use tools come from the dendextend (Galili 2015) and vegan (Oksanen et al. 2019) packages of the R programming language (R Core Team 2021). For the map of Turkey, we used Generic Mapping Tools (Wessel et al. 2019). To compute cophenetic distance matrix we used SageMath Developers et al. (2020). In order to compute and visualize clusters, we used python programming language (Van Rossum and Drake 2009) and its scikit-learn library (Pedregosa et al. 2011).

References

  • Adams H, Emerson T, Kirby M, Neville R, Peterson C, Shipman P, Chepushtanova S, Hanson E, Motta F, Ziegelmeier L (2017) Persistence images: a stable vector representation of persistent homology. J Mach Learn Res 18(1):218–252

    MathSciNet  MATH  Google Scholar 

  • Agresti A (2019) An introduction to categorical data analysis. Wiley Series in Probability and Statistics. John Wiley & Sons, Inc., Hoboken, NJ. Third edition of [ MR1394195]

  • Ben-Hur A, Horn D, Siegelmann HT, Vapnik V (2002) Support vector clustering. J Mach Learn Res 2(2):125–137

    MATH  Google Scholar 

  • Bray JR, Curtis JT (1957) An ordination of upland forest communities of southern wisconsin. Ecol Monogr 27:325–349

    Article  Google Scholar 

  • Bubenik P (2015) Statistical topological data analysis using persistence landscapes. J Mach Learni Res 16(1):77–102

    MathSciNet  MATH  Google Scholar 

  • Buchin K, Buchin M, Byrka J, Nöllenburg M, Okamoto Y, Silveira RI, Wolff A (2012) Drawing (complete) binary tanglegrams: hardness, approximation, fixed-parameter tractability. Algorithmica 62(1–2):309–332

    Article  MathSciNet  Google Scholar 

  • Carlsson G (2020) Persistent homology and applied homotopy theory. In: Handbook of Homotopy Theory, pp. 297–329. Chapman and Hall/CRC

  • Carlsson G, Mémoli F (2008) Persistent clustering and a theorem of j. kleinberg. arXiv preprint arXiv:0808.2241

  • Carlsson G, Mémoli F (2010) Characterization, stability and convergence of hierarchical clustering methods. J Mach Learn Res 11:1425–1470

    MathSciNet  MATH  Google Scholar 

  • Carlsson G, Zomorodian A, Collins A, Guibas LJ (2005) Persistence barcodes for shapes. Int J Shape Model 11(02):149–187

    Article  Google Scholar 

  • Chung YM, Lawson A (2019) Persistence curves: A canonical framework for summarizing persistence diagrams. arXiv preprint arXiv:1904.07768

  • Cohen-Steiner D, Edelsbrunner H, Harer J (2007) Stability of persistence diagrams. Discret Comput Geom 37(1):103–120

    Article  MathSciNet  Google Scholar 

  • Developers TS, Stein W, Joyner D, Kohel D, Cremona J, Eröcal B (2020) Sagemath, version 9.0

  • Donaldson S (2011) Riemann surfaces, Oxford Graduate Texts in Mathematics, vol 22. Oxford University Press, Oxford

    Google Scholar 

  • Edelsbrunner H, Letscher D, Zomorodian A (2000) Topological persistence and simplification. In: Proceedings 41st annual symposium on foundations of computer science, pp. 454– 463. IEEE

  • Elkin Y, Kurlin V (2020) The mergegram of a dendrogram and its stability. arXiv preprint arXiv:2007.11278

  • Fernau H, Kaufmann M, Poths M (2010) Comparing trees via crossing minimization. J Comput Syst Sci 76(7):593–608

    Article  MathSciNet  Google Scholar 

  • Fisher RA (1936) The use of multiple measurements in taxonomic problems. Ann Eugen 7(2):179–188

    Article  Google Scholar 

  • Galili T (2015) dendextend: an R package for visualizing, adjusting and comparing trees of hierarchical clustering. Bioinformatics 31(22):3718–3720

  • Ghrist R (2008) Barcodes: the persistent topology of data. Am Math Soc, Bull, New Ser 45(1):61–75

  • Hartigan JA (1985) Statistical theory in clustering. J Classif 2(1):63–76

    Article  MathSciNet  Google Scholar 

  • Hubert L, Arabie P (1985) Comparing partitions. J Classif 2(1):193–218

    Article  Google Scholar 

  • Ignacio PSP (2020) Intrinsic hierarchical clustering behavior recovers higher dimensional shape information. arXiv preprint arXiv:2010.03894

  • Jain AK, Dubes RC (1988) Algorithms for clustering data. Prentice Hall Advanced Reference Series. Prentice Hall Inc, Englewood Cliffs, NJ

    MATH  Google Scholar 

  • Jardine N, Sibson R (1971) Mathematical taxonomy. John Wiley & Sons Ltd., London-New York-Sydney. Wiley Series in Probability and Mathematical Statistics

  • Johnson SC (1967) Hierarchical clustering schemes. Psychometrika 32(3):241–254

    Article  Google Scholar 

  • Kleinberg JM (2002) An impossibility theorem for clustering. In: Becker S, Thrun S, Obermayer K (eds) Advances in neural information processing systems 32. MIT Press, Neural Information Processing Systems, pp 446–453

  • Kuhn HW (2005) The hungarian method for the assignment problem. Naval Res Logist (NRL) 52(1):7–21

    Article  Google Scholar 

  • Lance GN, Williams WT (1967) A general theory of classificatory sorting strategies: 1. hierarchical systems. Comput J 9(4):373–380

    Article  Google Scholar 

  • Legendre P, Legendre L (2012) Numerical ecology, 3rd edn. Elsevier

  • Lumbreras A, Velcin J, Guégan M, Jouve B (2017) Non-parametric clustering over user features and latent behavioral functions with dual-view mixture models. Comput Stat 32(1):145–177

  • Mantel N (1967) The detection of disease clustering and a generalized regression approach. Canc Res 27:209–220

  • Melnykov V, Zhu X (2019) An extension of the \(K\)-means algorithm to clustering skewed data. Comput Stat 34(1):373–394

    Article  MathSciNet  Google Scholar 

  • Merelli E, Rucco M, Sloot P, Tesei L (2015) Topological characterization of complex systems: Using persistent entropy. Entropy 17(10):6872–6892

    Article  Google Scholar 

  • Miller H (2020) Handbook of homotopy theory. CRC Press/Chapman and Hall Handbooks in Mathematics Series. CRC Press, Boca Raton, FL

    Book  Google Scholar 

  • Moon C, Giansiracusa N, Lazar NA (2018) Persistence terrace for topological inference of point cloud data. J Comput Gr Stat 27(3):576–586

    Article  MathSciNet  Google Scholar 

  • Oksanen J, Blanchet FG, Friendly M, Kindt, R, Legendre P, McGlinn D, Minchin PR, O’Hara R, Simpson GL, Solymos P, Stevens MHH, Szoecs E, Wagner H (2019) vegan: Community ecology package. R package version 2.5-6. https://CRAN.R-project.org/package=vegan

  • Patrício M, Pereira J, Crisóstomo J, Matafome P, Gomes M, Seiça R, Caramelo F (2018) Using resistin, glucose, age and bmi to predict the presence of breast cancer. BMC Cancer 18:1–8

    Article  Google Scholar 

  • Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay E (2011) Scikit-learn: machine learning in python. J Mach Learn Res 12:2825–2830

    MathSciNet  MATH  Google Scholar 

  • R Core Team: R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria (2021)

  • Rosenberg A, Hirschberg J (2007) V-measure: A conditional entropy-based external cluster evaluation measure. In: Proceedings of the 2007 joint conference on empirical methods in natural language processing and computational natural language learning (EMNLP-CoNLL), pp. 410–420

  • Rousseeuw PJ (1987) Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J Comput Appl Math 20:53–65

    Article  Google Scholar 

  • Scornavacca C, Zickmann F, Huson DH (2011) Tanglegrams for rooted phylogenetic trees and networks. Bioinformatics 27(13):i248–i256

    Article  Google Scholar 

  • Sergios T, Konstantinos K (2009) Pattern recognition, fourth, edition. Academic Press, Boston

    MATH  Google Scholar 

  • Sneath, PH, Sokal RR et al (1973) Numerical taxonomy. the principles and practice of numerical classification. W.H. Freeman and Company San Franscisco

  • Sokal RR, Rohlf FJ (1962) The comparison of dendrograms by objective methods. Taxon 11(2):33–40

    Article  Google Scholar 

  • Stong RE (1968) Notes on cobordism theory. Mathematical notes. Princeton University Press, Princeton, N.J.; University of Tokyo Press, Tokyo

  • Strehl A, Ghosh J (2002) Cluster ensembles-a knowledge reuse framework for combining multiple partitions. J Mach Learn Res 3:583–617

    MathSciNet  MATH  Google Scholar 

  • Van Rossum G, Drake FL (2009) Python 3 Reference Manual. CreateSpace, Scotts Valley, CA

    Google Scholar 

  • Wessel P, Luis JF, Uieda L, Scharroo R, Wobbe F, Smith WHF, Tian D (2019) The generic mapping tools version 6. Geochem, Geophys, Geosyst 20(11):5556–5564

    Article  Google Scholar 

  • Zomorodian A, Carlsson G (2005) Computing persistent homology. Discret Comput Geom 33(2):249–274

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The first author was supported by Research Fund Project Number TDK-2020-42698 of the Istanbul Technical University.

Author information

Authors and Affiliations

  1. Department of Mathematics Engineering, Istanbul Technical University, Istanbul, Turkey

    İsmail Güzel & Atabey Kaygun

Authors
  1. İsmail Güzel
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Atabey Kaygun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to İsmail Güzel.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Güzel, İ., Kaygun, A. A new non-archimedean metric on persistent homology. Comput Stat 37, 1963–1983 (2022). https://doi.org/10.1007/s00180-021-01187-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00180-021-01187-z

Keywords

Search

Navigation