1 Introduction

In the reciprocating cycle of the NC machine tool, the positioning precision of the ball screw system is primarily affected by the temperature rise. Different machine speeds are required according to the processing requirements. The temperature rise of the screw varies as the residence time of the nut on the screw surface changes with speed. The temperature rise of the ball screw is calculated using a traditional heat conduction model. The analytical solution of the mathematical model describes the exponential relationship between the temperature rises of the ball screw. Experimental temperature rise data are needed to improve the coefficient to fit the temperature field distribution. Furthermore, the formula of the friction heat source follows bearing theory [1,2,3,4,5,6], which does not take the groove parameters of the screw into account. Additionally, the friction torque varies with the temperature, which is also not considered when analyzing the temperature field of the ball screw. Therefore, it is essential to analyze the friction heat of the screw systematically to achieve good engineering practice.

In recent years, mathematical methods have been used to fit the temperature field of the ball screw system. These include the modified lumped capacitance method (MLCM), which was adopted to simulate the temperature distribution [7] by fitting the coefficients of a formula based on the measured temperature data. The exponential function provides the temperature curve of the screw detection point on the screw surface [8]. In [9], the multiple regression method (MRM) was proposed to predict the thermal error, and the regression coefficient was estimated from sampling data. A modified lumped approach (MLA) was adopted in [10] to optimize the finite element method (FEM) results for the temperature distribution in a ball screw system and reduce the discrepancy between the FEM estimate and measurement. In [11], MLCM compensation coefficients were obtained by fitting the model to the measured temperature data, and a genius education algorithm (GEA) was applied to minimize the error between the model and the measured data. In [7], the FEM was used to simulate the temperature field with and without air cooling; the screw was simplified as a shaft during the analysis. In [12], the temperature increase of a ball screw feed drive system was simulated using the FEM, and the model of the screw was also simplified as a solid shaft. In [13], the finite difference method (FDM) and response surface methodology (RSM) were applied to analyze the thermal characteristics of the ball screw feed considering a moving heat source. The study in [14] treated the nut as a moving heat source and used the FDM to simulate the temperature field and thermal error of the ball screw feed system under different working conditions. The authors of [15] proposed using the RSM to determine thermal boundary conditions that would improve the accuracy of simulating an analytical model of the traditional transient thermal characteristics of the ball screw feed system. In [16], thermal network analysis was used to calculate thermal errors in screw systems under various operating conditions. The study in [17] combined the FEM with the Monte Carlo (MC) method to estimate thermal boundary conditions for a machine tool feed system. In [18], an inverse random radial basis function neural network (IR-RBFNN) and forward random radial basis function neural network (FR-RBFNN) were proposed to predict thermal error considering the randomness of influencing factors. The study in [19] established a partial differential equation (PDE) model of the ball screw considering the unsteady local heat source and heat conduction between the screw shaft and machine bed to compensate thermal errors piecewise. All of the above methods excluded the screw raceway as a parameter. They were either based on known experimental data for fitting coefficients or required a lot of calculation, so they cannot be well applied in engineering practice.

Because friction torque and speed are the primary factors affecting the temperature rise of the ball screw, this article theoretically analyzes the friction heat generated by the motion of the nut and uses the segmentation method in this analysis. The groove parameters of the screw and the variation in friction torque with temperature are considered in the mathematical model, and then the steady temperature and stability time is deduced according to the friction torque and speed. The theoretical results are used to derive the temperature field equation of the screw, which can guide engineering applications.

2 Theoretical thermal analysis of the ball screw

During the ball screw system’s reciprocating circular motion, friction heat is generated at regular intervals for each section of the screw when contacting the nut. Some friction heat increases the inner power, and the rest is consumed for thermal conduction and thermal convection. However, the speed of the screw affects the friction heat and the time for the increase in internal energy. To analyze the temperature change of the screw due to the rise in internal energy when the screw contacts the nut, the friction heat of the screw and nut should be accurately modeled according to the speed, shape, and applied load of the screw.

In 2004, Tian [1] presented a formula for the heat generated by the nut as a function of the screw rotational velocity and the frictional torque of the nut, and other studies [2, 7, 20, 21] have used this formula to analyze the temperature rise of a ball screw. The formula is

$$q_{f} = 2\pi nM$$
(1)

where \(q_{f}\) is the heat per unit time generated by the nut (J/min), \(n\) is the screw rotational velocity (r/min), and \(M\) is the frictional torque of the nut (Nm).

Shi [8] modified the empirical formula for the heat generated by the nut:

$$q_{f} = 2\pi f_{0} \nu_{0} nM$$
(2)

where \(f_{0}\) is a factor related to the type of nut and method of lubrication, \(\nu_{0}\) is the kinematic viscosity of the lubricant, \(n\) is the screw rotational velocity, and \(M\) is the frictional torque of the nut.

However, although Eq. (2) introduces the effects of structural parameters, it is not a detailed calculation model and does not model the frictional torque.

2.1 Theoretical analysis of frictional heat

Because the friction from motion mainly causes the temperature rise between the ball and screw on the raceway surface, the friction heat formula for the screw when the nut is in contact with the screw is

$$q = f \cdot v$$
(3)

where f is the frictional force in the raceway of the screw and \(v\) is the sliding speed of the ball in the raceway.

2.1.1 Sliding speed

The sliding speed of the ball in the raceway is related to the groove parameters of the raceway according to

$$v = nl_{p} /\sin \gamma$$
(4)

where \(n\) is the rotational speed, \(l_{p}\) is the lead of the screw, and \(\gamma\) is the helix angle.

2.1.2 Friction force

A double-nut ball screw effectively eliminates raceway surface clearance, improves machining accuracy and structural stiffness, and is better for use in engineering. The friction force for a double-nut ball screw is produced at the contact point, and then the friction force can be derived from the friction torque through the following formulas [22]:

$$f_{Sj} = \frac{{M_{Sj} }}{{(r_{m} - r_{b} \cdot \cos \alpha_{Sj} )}}$$
(5)
$$f_{Nj} = \frac{{M_{Nj} }}{{(r_{m} + r_{b} \cdot \cos \alpha_{Nj} )}}$$
(6)

where \(f_{Sj}\) and \(f_{Nj}\) are the frictions on the screw raceway surface and nut raceway surface, respectively; \(M_{Sj}\) is the friction torque on the screw raceway surface and \(M_{Nj}\) the friction torque on the nut raceway surface; \(j = L\) or R, where \(j = L\) denotes the contact with the left raceway and \(j = R\) the contact with the right raceway; \(\alpha_{Sj}\) is the angle of contact with the screw and \(\alpha_{Nj}\) the angle of contact with the nut; \(r_{m}\) is the pitch radius of the screw and \(r_{b}\) the radius of the ball.

2.1.3 Formula for friction heat

Introducing the friction into the formulas of heat generation yields the following friction heat equations:

$$q_{fSj} = \frac{{l_{p} }}{{\sin \gamma (r_{m} - r_{b} \cdot \cos \alpha_{Sj} )}}nM_{Sj}$$
(7)
$$q_{fNj} = \frac{{l_{p} }}{{\sin \gamma (r_{m} + r_{b} \cdot \cos \alpha_{Nj} )}}nM_{Nj}$$
(8)

Simplifying formulas (7) and (8) yield the final frictional heat formulas:

$$q_{fSj} = \frac{2\pi }{{\cos \gamma }}nM_{Sj}$$
(9)
$$q_{fNj} = \frac{2\pi }{{\cos \gamma }}nM_{Nj}$$
(10)

According to formulas (9) and (10), the friction heat of the ball screw in unit time should be related to the spiral angle. In this paper, when the influence of friction torque on temperature rise is not considered, the friction heat is 1.008 times the traditional friction heat per unit time using the model parameters in Table 1.

Table 1 Structural parameters and experimental conditions
Full size table

2.2 Friction torque of the ball screw

The total friction torque for a ball screw with lubrication grease includes the Coulomb friction torque \(M_{ij}^{Q}\) and viscous friction torque \(M_{ij}^{g}\), so the friction torque in the contact area can be expressed as

$$M_{ij} { = }M_{ij}^{Q} + M_{ij}^{g} \;\left( {i = S \, or \, N} \right)$$
(11)

The Coulomb friction torque is related to the structural parameter and contact load according to [23]

$$M_{ij}^{Q} = \frac{{l_{p} }}{4\pi }\frac{\mu /(\tan \gamma ) + \mu \tan \gamma }{{(\sin \alpha_{ij} \cos \gamma - \mu \tan \gamma )(\sin \alpha_{ij} \cos \gamma + \mu \tan \gamma )}}Q_{ij}$$
(12)

where \(\mu { = }0.003\) is the raceway surface friction coefficient; \(Q_{ij}\) is the load at the contact point between the ball and screw or nut.

The viscous friction torque is related to the viscosity of the lubrication oil or grease via

$$M_{ij}^{g} = \frac{{\pi nd_{m} z}}{60\cos \gamma }\frac{{\eta_{ij} }}{{h_{ij} }}S_{ij} (r_{m} + \hat{k}r_{b} \cos \alpha_{ij} )$$
(13)

where \(S_{ij}\) is the contact area of the ball in the raceway, and \(S_{ij} { = }\pi a_{ij} b_{ij}\) [24] at high speed; \(a_{ij}\) and \(b_{ij}\) are the short and long half axes of the contact ellipse when the ball is in contact with the raceway surface, respectively; \(i = N\) or S, where \(i = N\) denotes the nut, \(i = S\) denotes the screw, \(\hat{k}{ = }1\) when \(i{ = }N\), and \(\hat{k}{ = } - 1\) when \(i{ = }S\); \(d_{m}\) is the pitch diameter of the screw.

The viscosity of the lubrication oil or grease is given by

$$\eta_{ij} { = }\eta_{0} e^{a \times (c - 1)}$$
(14)

where \(a{ = }\ln \eta_{0} + 9.67\) and \(c{ = }(1 + 5.1 \times 10^{ - 9} p)^{0.68} \times [(T - 138)/(T_{0} - 138)]^{ - 1.1}\)[25] (\(p\) is the pressure).

The film thickness of the lubrication oil or grease is given by [24]

$$\hbar_{ij} = 2.69R_{x} U_{e}^{0.67} G^{0.53} W^{ - 0.067} (1 - 0.61e^{ - 0.73k} )$$
(15)

where \(k\) is the dimensionless ellipticity of the screw shaft and nut contact given by \(k = 1.0339(R_{x} /R_{y} )^{0.636}\); \(U_{e} = u\eta /(E^{\prime}R_{x} )\), where \(u\) is the entraining surface velocity, and \(\eta\) is the lubricant viscosity at solid body temperature and ambient pressure; \(G = \overline{\alpha }E^{\prime}\), where \(\overline{\alpha }\) is the pressure–viscosity coefficient; \(W = w/(E^{\prime}R_{x}^{2} )\), where \(E^{\prime}\) is the equivalent elastic modulus, \(R_{x}\) is the radius of curvature, and \(w\) is the load.

2.2.1 Analysis of absolute viscosity and film thickness

The friction torque on a ball screw depends on the lubricant viscosity and film thickness. The lubricant viscosity and film thickness are both affected by the temperature. Figure 1 shows the variation in absolute viscosity for two kinds of viscous greases at 1000 rpm with changing temperature. These are grease A with a viscosity of 0.34 Pa·s at 40 °C and grease B with a viscosity of 0.58 Pa·s at 40 °C. The absolute viscosity decreases as the temperature increases. As the temperature rises from 20 to 70 °C, the lubricant viscosity at atmospheric pressure decreases by 92.57% from 1.1597 to 0.0862 Pa·s for grease A and by 93.67% from 2.1351 to 0.135 Pa·s for grease B.

Fig. 1
figure 1

Variation in viscosity with temperature for sample 1 with two different greases

Full size image

Figure 2 shows the variation in film thickness at 1000 rpm with changing temperature. The film thickness decreases as the temperature increases. As the temperature rises from 20 to 70 °C, the film thickness decreases by 84.6% from 0.13 to 0.02 mm for grease A and by 84.2% from 0.19 to 0.03 mm for grease B.

Fig. 2
figure 2

Variation in film thickness with temperature for sample 1 with two different greases

Full size image

2.2.2 Simulation of friction torque

Figure 3 shows the friction torque predictions for speeds from 1000 to 3000 rpm and temperatures from 20 to 70 °C with two kinds of viscous greases for sample 1 in this paper. The results shows that the friction torque is significantly affected by temperature. As the temperature changes from 20 to 70 °C, the friction torque decreases by 22% from 0.59 to 0.46 Nm for grease A and by 33.8% from 0.71 to 0.47 Nm for grease B at 1000 rpm. At 3000 rpm, the friction torque decreases by 44.94% from 0.89 to 0.49 Nm for grease A and by 58.37% from 1.25 to 0.52 Nm for grease B. Comparing Fig. 3a and b shows that the influence of viscosity on friction torque is strong at low temperature but gradually decreases with increasing temperature. These results confirm that the lubricant temperature significantly affects the ball screw friction torque.

Fig. 3
figure 3

Variation in friction torque with speed and temperature for sample 1 for two different greases

Full size image

2.3 Thermal convection coefficient for the screw

The following equation is used to analyze the heat convection coefficient:

$$h = ({{\lambda^{*} } \mathord{\left/ {\vphantom {{\lambda^{*} } d}} \right. \kern-0pt} d}) \cdot Nu$$
(16)

where \(\lambda^{*}\) is the heat transfer coefficient of air, \(d\) is the diameter of the screw, and \(Nu\) is the Nusselt number.

The Nusselt number [26] is

$$Nu = 0.133Re^{2/3} Pr^{1/3}$$
(17)

where \(Pr\) is the Prandtl number. The Reynolds number for the screw is calculated as

$$Re = {{\omega \cdot d^{2} } \mathord{\left/ {\vphantom {{\omega \cdot d^{2} } {\upsilon^{*} }}} \right. \kern-0pt} {\upsilon^{*} }}$$
(18)

where \(\omega\) is the angular speed of the screw given by \(\omega = 2\pi n\), and \(\upsilon^{*}\) is the kinematic viscosity of air.

Then,

$$h=0.133\cdot\lambda^\ast\omega^{2/3}d^{1/3}\upsilon^{\ast-2/3}{Pr}^{1/3}$$
(19)

3 Steady temperature and stability time analysis

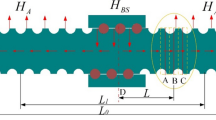
To better analyze the thermal friction dynamics of the screw, the screw is divided into sections according to the length of the nut. The stroke of the screw is assumed to have three times the length of the nut, as shown in Fig. 4. The nut is defined as a moving heat source. For the middle area of the screw in the stroke (position ①), the heat transfer between the left and right nuts is integrated, and the heat is the sum of the friction heat of the two nuts. For the areas close to the middle area of the screw (position②), the heat is the sum of the friction heat of one nut and half that of the other nut. However, the heat transfer is uneven at both ends of the screw (position③), and the friction heat at both ends is only half that of the single nut. The uneven heat distribution causes an uneven temperature rise in the screw stroke during motion, producing a specific temperature difference. In addition, the heat convection is ongoing because it is directly related to the temperature difference between the screw and the environment. The convection is greater when the temperature difference is higher. Therefore, in the heating of the screw, the thermal convection between the screw and the environment grows until the heat input and output equal each other. The temperature of the screw surface will be in thermal equilibrium.

Fig. 4
figure 4

Single reciprocating process of thermal motion for screw sections

Full size image

As shown in Fig. 4, the number of sections of the screw is based on the total contact length \(S_{o}\) of the screw and the length \(l_{n}\) of the nut:

$$N = S_{o} /l_{n}$$
(20)

The duration of a single contact is

$$\Delta t_{0} = 60l_{n} /(nl_{p} )$$
(21)

The time taken for a single cycle can be obtained as

$$\Delta t{ = }(N - 1)\Delta t_{o}$$
(22)

where \(N\) is the number of screw sections according to the length of the nut.

3.1 Steady-state temperature analysis

On the basis of the above analysis, the heat transfer of the screw in the middle area is close to that of the adjacent area and greater than that of the boundary area. The heat conduction is inversely proportional to the distance, so the heat conduction decreases with decreasing distance and temperature difference. Then considering the heat convection on the middle area of the screw, the screw surface temperature will reach a steady state when the input heat of the screw is equal to the heat transfer with the environment, and the following relation can be deduced:

$$(N - 2)q_{{f_{S} }} \Delta t_{0} = (q_{{f_{SL} }} + q_{{f_{SR} }} )\Delta t_{0}$$
(23)

The expression for convectional heat is

$$\overline{q}_{S} = h_{S} A_{S} \Delta T$$
(24)

Then, the steady-state growth temperature can be obtained as

$$\Delta T{ = }\frac{{q_{{f_{SL} }} + q_{{f_{SR} }} }}{{(N - 2)h_{S} A_{S} }}$$
(25)

where \(A_{S}\) is the heat dissipation area of the screw given by \(A_{S} = \pi d_{m} l_{n}\), and \(h_{S}\) is the thermal convection coefficient of the screw surface.

Substituting the velocity from Eq. (4) into Eq. (19) gives

$$\Delta T=\frac{7.519(q_{f_{SL}}+q_{f_{SR}})\omega^{-2/3}}{(N-2)\pi\cdot\lambda^\ast d_m^{4/3}\upsilon^{\ast-2/3}{Pr}^{1/3}l_n}$$
(26)

When \(\alpha_{SL} = \alpha_{SR}\), Eq. (26) can be simplified as

$$\Delta T{ = }\phi n^{1/3} (M_{SL}^{Q} + M_{SR}^{Q} + M_{SL}^{g} + M_{SR}^{g} )$$
(27)

where \(\phi\) is a coefficient related to the structural parameters of the ball screw and the external environment according to

$$\phi =\frac{2.42}{\left(N-2\right){\pi }^\frac{2}{3} {\lambda }^{*}{d}_{m}^\frac{4}{3}{\upsilon }^{*-\frac{2}{3}}{Pr}^\frac{1}{3}{l}_{n}\mathrm{cos}\gamma }$$
(28)

It can be shown that, when the friction torque is invariable, the steady-state temperature of the screw is proportional to the third power of the speed.

3.2 Stability time analysis

When the screw is in constant cyclic motion, the heat input is equal to the increase in internal energy and the heat lost through heat convection. Then, the heat balance formula of the screw is

$$\hat{n}(q_{{f_{SL} }} + q_{{f_{SR} }} ) \times \Delta t_{0} - \hat{n}\Delta t_{0} (N - 2)q_{S} = cm_{m} \Delta T$$
(29)

where \(\hat{n}\) is the number of reciprocating motions, and \(\hat{n} = t_{S} /\Delta t\).

Then, the stability time for the effective heat source section of the screw can be obtained as

$$t_{S} = \frac{{{(}N - 1{)}cm_{m} \Delta T}}{{(q_{{f_{SL} }} + q_{{f_{SR} }} ) - (N - 2)h_{S} A_{S} \sum {\Delta T_{\varepsilon } } }}$$
(30)

where \(\Delta T_{\varepsilon }\) is each temperature rise in the superposition given by \(\Delta T_{\varepsilon } { = }\chi \Delta T\), where \(\chi\) is the temperature distribution coefficient.

The stability time can be shown to be independent of the friction torque but related to the speed.

When the ball screw is suspended during operation, its heat balance formula is

$$\hat{n}(q_{{f_{SL} }} + q_{{f_{SR} }} ) \times \Delta t_{0} - \hat{n}\Delta t_{0} (N - 2)q_{S} - q^{\prime}_{S} \Delta t^{\prime} = cm_{m} \Delta T$$
(31)

where \(q^{\prime}\) denotes the convection heat loss during the pause period, \(q^{\prime}_{S} = h^{\prime}_{S} A_{S} \Delta T\), \(h^{\prime}_{S}\) is the natural convection coefficient of air, and \(\Delta t^{\prime}\) is the suspension time.

The stability time for the effective heat source section of the screw is obtained from

$$t_{S} = \frac{{(N - 1)(cm_{m} \Delta T + h^{\prime}_{S} A_{S} \Delta t^{\prime}\sum {\Delta T_{\varepsilon } } )}}{{(q_{{f_{SL} }} + q_{{f_{SR} }} ) - (N - 2)h_{S} A_{S} \sum {\Delta T}_{\varepsilon } }}$$
(32)

3.3 Solutions for the temperature field parameters

According to the traditional heat conduction model, the temperature rise of each point on the ball screw surface is exponential with time [8], which can be expressed as

$$T(t) = T_{0} + c_{T} (1 - e^{ - \tau t} )$$
(33)

Combined with the above theoretical analysis, \(T(t) \to T_{s}\) when the temperature is stable and \(t > t_{S}\), where \(T_{s} { = }T_{0} + \Delta T\); \(T_{0}\) is the initial temperature; \(c_{T} = \Delta T\); \(\tau\) is the exponential percentage given by \(\tau = t_{0} /t_{S}\), where \(t_{0}\) is the heating time for the screw section to reach the stable temperature \(\Delta T\) supposing the nut is a fixed heat source, and \(t_{S}\) from Eq. (32) is the time when the screw reaches the steady-state temperature.

4 Experimental verification

The experimental facility is shown in Fig. 5. The ball screw is supported by the bearings of both ends and the middle nut seat. The driving end is fixedly connected with the main shaft of the motor with a coupling; the tail support unit supports the other end to reduce the influence of installation on temperature rise. The nut seat is guided by a bottom guide rail. The motion program is edited in advance in a Siemens control system. When the program starts, the drive control system receives signals to drive the screw to rotate. The screw raceway surface moves the ball screw to squeeze the nut for axial motion. In this experimental scheme, the nut flange and nut seat are installed in reverse, mainly to facilitate detection of the nut surface temperature to reduce the influence of the nut seat. After the experiment, the device was cooled in a constant-temperature chamber with forced wind for more than 6 h. After the end of the investigation, the lubricating medium was cleaned with a special cleaning agent for the screw, and another lubricating medium was added after the static constant greenhouse was dried entirely naturally. Many researchers have used a thermal imager to monitor the surface temperature of ball screws. However, the surface of the screw is arc-shaped and the measurement stability is not high, so a TES 1310 Type-K contact thermometer was used to detect the temperature to improve precision.

Fig. 5
figure 5

Temperature measurement facility

Full size image

4.1 Test procedure

The test was mainly carried out via real-time temperature detection at four points, three points on the screw and one on the nut surface. The stroke was set as three times the length of the nut, as shown in Fig. 4. In the experiment, we selected sample pre-tightened double-nut ball screws from two different manufacturers and two kinds of grease with different viscosities to verify the theoretical analysis. The speed was set to 1000 rpm, 2000 rpm, and 3000 rpm. We measured the temperature rise in a constant-temperature greenhouse with an ambient temperature of 21 ± 2 °C. In the middle of the process, the program set a pause time of 60 s to measure the temperature. For better temperature monitoring in the early stage, the temperature of the screw and nut were measured at three intervals: 10 times at an interval of 2000 r, 10 times at an interval of 5000 r, and 10 times at an interval of 10,000 r. The structural parameters used in the experiment are shown in Table 1. The experimental scheme (abbreviated as “S”) is shown in Table 2.

Table 2 Test parameters used in the experiment
Full size table

4.2 Comparison between the experimental and theoretical values

4.2.1 Temperature field in the middle area of the screw

According to the analysis in Section 3.2, the steady-state time is 102.1 min at 1000 rpm, 44.4 min at 2000 rpm, and 30.2 min at 3000 rpm. Putting these into formula (33) yields the theoretical temperature rise curve of the middle area of the screw, which is shown as the solid line in Figs. 6 and 7. The solid angular markers represent the measured values. The maximum error between the theoretical and measured results is less than 10% in the steady state, which verifies the theoretical analysis.

Fig. 6
figure 6

Temperature rising for sample 1

Full size image
Fig. 7
figure 7

Temperature rise for sample 2

Full size image

Before the screw reaches a steady state, the temperature presents a parabolic upward trend. The upward range gradually decreases with time. The temperature of the screw increases with increasing speed because the temperature rise caused by the friction heat is mainly influenced by speed and friction torque. When the friction heat reaches a thermal balance with the external environment, the temperature becomes stable, and the friction torque does not change.

The analysis in Table 3 shows that the steady-state temperatures of sample 1 at the speeds of 2000 rpm and 3000 rpm and sample 2 at all three rates are mainly affected by the velocity; the effect of friction torque has little effect and can be neglected. However, the impact of friction torque is not negligible for sample 1 at 1000 rpm. The friction torque includes Coulomb friction torque and viscous friction torque, which is affected by the temperature. When the viscous friction torque accounts for a small proportion of the total friction torque, the steady-state temperature of the screw is mainly related to the speed. For sample 1 with two kinds of lubricating grease, the temperature rises of the screw at 2000 rpm and 3000 rpm follow the speed ratio \(\Delta T_{{v_{2} }} /\Delta T_{{v_{1} }} = i^{1/3}\) (\(i\) is the speed ratio, \(i{ = }v_{2} /v_{1}\)); for sample 2, the relationship between the temperature rise of the screw and the speed also follows the connection.

Table 3 Reference parameters and fitting curve formula for theoretical prediction
Full size table

4.2.2 Overall temperature rise distribution of the ball screw

Owing to the long travel used for the test bed, the temperature rise of the screw near the bearing end was found to be only 4–5 °C when the temperature rise of the screw surface reached 40 °C after 2 h of running. Therefore, the influence of the bearing on the temperature rise of the screw was ignored in these investigations.

The friction torque parameters include the contact load and contact area on the raceway surfaces, which directly affect the contact thermal resistance between the ball and the screw and nut, thus affecting the heat conduction between them. However, the contact area of the ball on the raceway surface is tiny owing to the extreme rigidity of the ball screw. The contact time in the raceway is short when the ball moves at high speed, and when the temperature discrepancy between the ball and the screw and the nut is insignificant, the heat transferred per unit time is very low relative to the heat convection.

According to the analysis in Section 3 for the double-nut ball screw, the heat received in each area of the screw stroke is different, so the temperature rise also varies. For the middle area of the screw in the stroke, the heat transfer between the left and right nuts is integrated, so the highest temperature rises. Still, the heat transfer is uneven on both ends of the screw, the friction heat on both end areas is only half that of the single nut, and the temperature rise is the lowest. For the areas close to the middle area of the screw, the heat is the sum of the friction heat of one nut and half of the other nut, the temperature is higher than at the end area of the screw and lower than in the middle area of the screw. Figures 8 and 9 show the measured temperatures of three points on the screw surface and one point on the nut surface in the 12 schemes. The three points on the screw surface correspond to the positions of the three points in Fig. 4. The temperature error in the steady state between the nut and point 1 of the screw is defined as \(\Delta T_{n - 1}\), that between point 1 and point 2 of the screw is defined as \(\Delta T_{1 - 2}\), and that between points 1 and 3 is defined as \(\Delta T_{1 - 3}\). The test results show that the temperature rise of the nut approaches the middle area of the screw. Still, the temperature difference of point 3 is much more significant than that of point 2 or point 1. This further verifies the temperature rise theory in this paper.

Fig. 8
figure 8

Temperatures of the nut and points 1–3 of the ball screw with a contact load of 5136 N. a, c, e Grease A (40 °C). b, d, f Grease B (40 °C)

Full size image
Fig. 9
figure 9

Temperatures of the nut and points 1–3 of the ball screw with a contact load of 5589 N. a, c, e Grease A. b, d, f Grease B

Full size image

5 Conclusions

Friction heat is an essential factor in ball screw thermal deformation. At present, analysis is based on test data or experimentally measured results and lacks a theoretical basis. Therefore, we embarked on a theoretical study to establish a mathematical model of friction heat. We investigated the influences of two factors, velocity and friction torque, on temperature rise. The analysis has led to the following findings and conclusions:

  1. 1.

    The friction heat distribution of the screw in the stroke is different. The nut is a moving heat source. For the middle area of the screw in the stroke, the heat transfer between the left and right nuts is integrated; the heat is the sum of the friction heat of the two nuts. Still, the heat transfer is uneven on both ends of the screw; the friction heat on both end areas is only half that of the single nut. For the areas close to the middle area of the screw, the heat is the sum of the friction heat of one nut and half that of the other nut. The uneven heat distribution causes the uneven temperature rise in the screw stroke, producing a specific temperature difference. Therefore, the temperature of the middle area of the screw is the highest, that of the adjacent areas of the screw is a little lower than that of the middle area, and both ends have the lowest temperature.

  2. 2.

    The surface temperature rise curve of the screw can be determined by theoretically predicting the steady-state temperature and steady-state time. A steady-state temperature model can be established when the frictional heat is equal to the external heat flow and the temperature becomes stable. The stability time can be deduced from the steady-state temperature. The surface temperature distribution of the screw with time can be fitted with an exponential function. Furthermore, the steady-state temperature increases with higher screw speed, and the stability time shortens.

  3. 3.

    The friction torque is affected by temperature. Friction torque is divided into load friction torque and viscous friction torque. The load friction torque is mainly affected by the load, and the viscous friction torque is affected by the temperature at a constant speed. The load friction torque does not change with the temperature since the friction coefficient is constant. The viscous friction torque decreases with the increase in temperature when the ball screw heats up. At low temperature, the friction torque is large, and the temperature of the screw rises fast. When the temperature of the screw increases, the friction torque decreases, and the temperature rise slows down.

  4. 4.

    There is a numerical relationship between the temperature rise and speed ratio of the ball screw. When the temperature increases greatly, the viscosity has little effect on the temperature rise. Then the temperature rise at two speeds follows the relationship \(\Delta T_{{v_{2} }} /\Delta T_{{v_{1} }} = i^{1/3}\)(\(i\) is the speed ratio, \(i{ = }v_{2} /v_{1}\)).