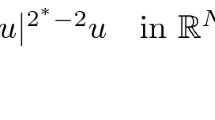Abstract
In this paper, we study the existence of critical points for the following functional constrained on \({S_c=\{u\in H^1(\mathbb{R}^N)| |u|_2=c\}}\):
where N = 1, 2, 3 and a, b > 0 are constants. The constraint problem is L 2-critical. We showed that I(u) has a constraint critical point with a mountain pass geometry on S c if \({c > c^*:=(2^{-1}b|Q|_2^{\frac{8}{N}})^{\frac{N}{8-2N}}}\), where Q is the unique positive radial solution of \({-2\Delta Q+(\frac{4}{N}-1)Q=|Q|^{\frac{8}{N}} Q}\) in \({\mathbb{R}^N}\). For 0 < c < c *, I(u) has no critical point on S c , and we proved the existence of minimizers for a new perturbation functional on S c :
Similar content being viewed by others
References
Alves C.O., Crrea F.J.S.A.: On existence of solutions for a class of problem involving a nonlinear operator. Commun. Appl. Nonlinear Anal. 8, 43–56 (2001)
Arosio A., Panizzi S.: On the well-posedness of the Kirchhoff string. Trans. Am. Math. Soc. 348(1), 305–330 (1996)
Bellazzini J., Jeanjean L., Luo T.J.: Existence and instability of standing waves with prescribed norm for a class of Schrödinger–Poisson equations. Proc. Lond. Math. Soc. 107(2–3), 303–339 (2013)
Bernstain S.: Sur une classe d’équations fonctionelles aux dérivées partielles. Bull. Acad. Sci. URSS. Sér. 4, 17–26 (1940)
Bellazzini J., Siciliano G.: Scaling properties of functionals and existence of constrained minimizers. J. Funct. Anal. 261, 2486–2507 (2011)
Cavalcanti M.M., Domingos Cavalcanti V.N., Soriano J.A.: Global existence and uniform decay rates for the Kirchhoff–Carrier equation with nonlinear dissipation. Adv. Differ. Equ. 6(6), 701–730 (2001)
D’Ancona P., Spagnolo S.: Global solvability for the degenerate Kirchhoff equation with real analytic data. Invent. Math. 108(2), 247–262 (1992)
Guo Y.J., Seiringer R.: On the mass concentration for Bose–Einstein condensates with attractive interactions. Lett. Math. Phys. 104, 141–156 (2014)
He X.M., Zou W.M.: Existence and concentration behavior of positive solutions for a Kirchhoff equation in \({\mathbb{R}^3}\). J. Differ. Equ. 252, 1813–1834 (2012)
Jeanjean L.: Existence of solutions with prescribed norm for semilinear elliptic equations. Nonlinear Anal. Theory T. M. & A. 28(10), 1633–1659 (1997)
Jeanjean L., Luo T.J.: Sharp nonexistence results of prescribed L 2-norm solutions for some class of Schrödinger–Poisson and quasi-linear equations. Z. Angrew. Math. Phys. 64(4), 937–954 (2013)
Jin J.H., Wu X.: Infinitely many radial solutions for Kirchhoff-type problems in \({\mathbb{R}^N}\). J. Math. Anal. Appl. 369, 564–574 (2010)
Kirchhoff, G.: Mechanik. Teubner, Leipzig (1883)
Li G.B., Ye H.Y.: Existence of positive ground state solutions for the nonlinear Kirchhoff type equations in \({\mathbb{R}^3}\). J. Differ. Equ. 257, 566–600 (2014)
Li, G.B., Ye, H.Y.: Existence of positive solutions for nonlinear Kirchhoff type problems in \({\mathbb{R}^3}\) with critical Sobolev exponent. Math. Methods Appl. Sci. 37, 2570–2584 (2014)
Li Y. et al.: Existence of a positive solution to Kirchhoff type problems without compactness conditions. J. Differ. Equ. 253, 2285–2294 (2012)
Lions J.L.: On some questions in boundary value problems of mathmatical physics. In: Contemporary Development in Continuum Mechanics and Partial Differential Equations, North-Holland Math. Stud., Vol. 30, North-Holland, Amsterdam, New York, pp. 284–346 (1978)
Lions P.L.: The concentration-compcatness principle in the calculus of variations. The locally compact case. I.. Ann. Inst. H. Poincaré Anal. NonLinéaire 1, 109–145 (1984)
Liu W., He X.M.: Multiplicity of high energy solutions for superlinear Kirchhoff equations. J. Appl. Math. Comput. 39, 473–487 (2012)
Pohozaev, S.I.: A certain class of quasilinear hyperbolic equations. Mat. Sb. (NS) 96 (138) (1975) 152–166, 168 (in Russian)
Sun J.T., Wu T.F.: Ground state solutions for an indefinite Kirchhoff type problem with steep potential well. J. Differ. Equ. 256, 1771–1792 (2014)
Wang J. et al.: Multiplicity and concentration of positive solutions for a Kirchhoff type problem with critical growth. J. Differ. Equ. 253, 2314–2351 (2012)
Weinstein M.I.: Nonlinear Schrödinger equations and sharp interpolation estimates. Commun. Math. Phys. 87, 567–576 (1983)
Willem, M.: Minimax Theorems, Progress in Nonlinear Differential Equations and Their Applications. Vol. 24, Birkhäuser, Boston (1996)
Wu X.: Existence of nontrivial solutions and high energy solutions for Schrödinger–Kirchhoff-type equations in \({\mathbb{R}^N}\). Nonlinear Anal. Real World Appl. 12, 1278–1287 (2011)
Ye, H.Y.: The sharp existence of constrained minimizers for a class of nonlinear Kirchhoff equations. Math. Methods Appl. Sci. doi:10.1002/mma.3247
Author information
Authors and Affiliations
Corresponding author
Additional information
Partially supported by NSFC No.: 11371159, NSFC No.: 11301204.
Rights and permissions
About this article
Cite this article
Ye, H. The existence of normalized solutions for L 2-critical constrained problems related to Kirchhoff equations. Z. Angew. Math. Phys. 66, 1483–1497 (2015). https://doi.org/10.1007/s00033-014-0474-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00033-014-0474-x