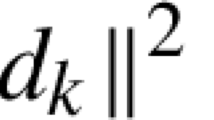1 Introduction

Polynomial root finding is one of the oldest and most deeply studied mathematical problems because of its many practical applications, e.g., in engineering [8], optimization [5], medicine [9], etc. In 2000, BC Babylonians solved quadratic equation. Since then, many different methods of numerical finding of polynomial’s roots have been introduced. The most widely known method is the Newton method [6]. Other popular methods that were introduced in the literature are: Helley method [2], Traub–Ostrowski method [31], Whittaker method [31], etc. Moreover, in the literature, one can find whole families of root finding methods, e.g., Euler–Schörder [19], Lotfi et al. [23], Cordero et al. [7], or Basic Family [19] introduced by Kalantari.

Kalantari introduced also the term polynomiography. He defined this term in the following way [18]: Polynomiography is the art and science of visualization in approximation of the zeros of complex polynomials, via fractal and non-fractal images created using the mathematical convergence properties of iteration functions. A single image created using the mentioned methods is called a polynomiograph. Polynomiography is used to graphically study root finding methods and their dynamics [2, 10, 31] or to generate images with an artistic value [10, 13, 18].

Because the root finding process can be equivalently transformed into a fixed point problem [6] in recent years, researchers have studied the use of various iteration processes—known in fixed point theory—that are used to find fixed points in the root finding methods. Gdawiec et al. in [12] proposed the use of ten different iteration methods, e.g., SP, Noor, Picard-S. Later, in [11], Gdawiec and Kotarski extended the list of iterations to seventeen different iterations. They also studied the dependencies between the iterations. In [21], Kang et al. used the S-iteration in Newton’s method to obtain a variety of different polynomiographs. The iteration methods used in [11, 12, 21] were all explicit iteration schemes. Rafiq et al. in [28] proposed the use of some implicit schemes in root finding, namely the Jungck, the Jungck–Mann, and Jungck–Ishikawa iterations. To combine the root finding methods and to obtain very interesting polynomiographs in [10], Gdawiec used iterations that find common fixed points of several functions. Numerical study on the use of various iteration schemes in root finding can be found in [3, 4, 10], whereas in [22, 29, 30], some theoretical study on the semi-local and local convergence of Newton-like methods with different iterations can be found.

In this paper, we propose a modification of the iteration processes used in the Basic Family of iterations [12] by replacing the convex combination with an s-convex one. Although, we present how to modify general iteration processes in the examples, we will concentrate only on the S-iteration. The presented examples are both graphical and numerical ones.

The paper is organized as follows. In Sect. 2, we introduce the Basic Family of iterations and the algorithm for computing value in a given point of the elements of this family. Next, in Sect. 3, we present how to modify iteration processes of the Basic Family of iterations using the s-convex combination. Then, in Sect. 4, we give the algorithm for the generation of polynomiograph. Some graphical and numerical examples showing the use of the proposed modifications are presented in Sect. 5. Finally, in Sect. 6, we give some concluding remarks.

2 Basic Family of Iterations

Let us consider a polynomial \(p \in \mathbb {C}[Z]\) and \(\deg p \ge 2\) of the form:

$$\begin{aligned} p(z) = a_n z^n + a_{n-1} z^{n-1} + \cdots + a_1 z + a_0. \end{aligned}$$
(1)

Now, we define a sequence of functions \(D_m: \mathbb {C} \rightarrow \mathbb {C}\) as follows [19]:

$$\begin{aligned} {\begin{matrix} D_0(z) = 1, \\ \forall _{m \in \{1, 2, \ldots \}} \quad D_m(z) &{}= \det \begin{pmatrix} p'(z) &{}\quad \frac{p''(z)}{2!} &{}\quad \ldots &{}\quad \frac{p^{(m-1)}(z)}{(m-1)!} &{}\quad \frac{p^{(m)}(z)}{m!}\\ p(z) &{}\quad p'(z) &{}\quad \ddots &{}\quad \ddots &{}\quad \frac{p^{(m-1)}(z)}{(m-1)!} \\ 0 &{}\quad p(z) &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \frac{p''(z)}{2!}\\ 0 &{}\quad 0 &{}\quad \ldots &{}\quad p(z) &{}\quad p'(z) \end{pmatrix}. \end{matrix}}\nonumber \\ \end{aligned}$$
(2)

Then, the Basic Family of iterations [19] is defined as:

$$\begin{aligned} B_m(z) = z - p(z) \frac{D_{m-2}(z)}{D_{m-1}(z)}, \end{aligned}$$
(3)

where \(m \in \{2, 3, 4, \ldots \}\).

When we look at the first elements of the family:

$$\begin{aligned} B_2(z)= & {} z - \frac{p(z)}{p'(z)}, \end{aligned}$$
(4)
$$\begin{aligned} B_3(z)= & {} z - \frac{2 p'(z) p(z)}{2 p'(z)^2 - p''(z) p(z)}, \end{aligned}$$
(5)
$$\begin{aligned} B_4(z)= & {} z - \frac{6 p'(z)^2 p(z) - 3 p''(z) p(z)^2}{p'''(z) p(z)^2 + 6 p'(z)^3 - 6 p''(z) p'(z) p(z)}, \end{aligned}$$
(6)

then we see that \(B_2\) is the standard first-order Newton root finding method, and \(B_3\) is the second-order method known as the Halley’s root finding method. Moreover, we can observe that when m increases, then the order of the corresponding root finding method also increases and its formula becomes more complex. To be able to efficiently compute values for any \(z \in \mathbb {C}\) of each of the family member, Jin and Kalantari in [15]—using the theory of symmetric functions—derived an algorithm for this aim (Algorithm 1).

figure a

The Basic Family has numerous fundamental properties. It is closely related to a non-trivial determinantal generalization of Taylor’s theorem [17]. For the multipoint version of the family and their order of convergence, see [17] and [16], respectively. For a detailed list of theoretical and computational properties, see [16, 17, 19, 20].

3 Basic Family of Iterations via Iterations with s-Convexity

To find a root of polynomial p using the elements of the Basic Family of iterations, we use the following feedback process:

$$\begin{aligned} z_{n+1} = B_m(z_n), \end{aligned}$$
(7)

where \(z_0 \in \mathbb {C}\) is the starting point. When we look at this process, then we can observe that this feedback process is the well-known Picard iteration [26]. In [12], Gdawiec et al. proposed to replace the Picard iteration with various iteration processes known from fixed point theory; for example:

  • Mann iteration [24]

    $$\begin{aligned} z_{n+1} = (1 - \alpha ) z_n + \alpha B_m(z_n), \end{aligned}$$
    (8)

    where \(\alpha \in (0, 1]\):

  • Ishikawa iteration [14]

    $$\begin{aligned} {\left\{ \begin{array}{ll} z_{n+1} = (1 - \alpha ) z_n + \alpha B_m(v_n), \\ v_n = (1 - \beta ) z_n + \beta B_m(z_n), \end{array}\right. } \end{aligned}$$
    (9)

    where \(\alpha \in (0, 1]\) and \(\beta \in [0, 1]\):

  • S-iteration [1]

    $$\begin{aligned} {\left\{ \begin{array}{ll} z_{n+1} = (1 - \alpha ) B_m(z_n) + \alpha B_m(v_n), \\ v_n = (1 - \beta ) z_n + \beta B_m(z_n), \end{array}\right. } \end{aligned}$$
    (10)

    where \(\alpha \in (0, 1]\) and \(\beta \in [0, 1]\):

  • Noor iteration [25]

    $$\begin{aligned} {\left\{ \begin{array}{ll} z_{n+1} = (1 - \alpha ) z_n + \alpha B_m(v_n), \\ v_n = (1 - \beta ) z_n + \beta B_m(w_n), \\ w_n = (1 - \gamma ) z_n + \gamma B_m(z_n), \end{array}\right. } \end{aligned}$$
    (11)

    where \(\alpha \in (0, 1]\) and \(\beta , \gamma \in [0, 1]\).

Looking at the iterations, we can observe that they can use different number of steps, but they all have a common property, namely they use a convex combination in each step. In the literature, we can find some generalizations of the convex combination. One of such generalizations is the s-convex combination [27].

Definition 3.1

Let \(z_1, z_2, \ldots , z_n \in \mathbb {C}\) and \(s \in (0, 1]\). The s-convex combination is defined in the following way:

$$\begin{aligned} \lambda _{1}^{s} z_1 + \lambda _{2}^{s} z_2 + \cdots + \lambda _{n}^{s} z_n, \end{aligned}$$
(12)

where \(\lambda _k \ge 0\) for \(k \in \{ 1, 2, \ldots , n \}\) and \(\sum _{k = 1}^{n} \lambda _k = 1\).

Let us notice that the s-convex combination reduces to the convex one for \(s = 1\).

In [10], we can find application of the s-convex combination in root finding methods and polynomiography. Gdawiec used this type of combination to create a combination of root finding methods. We will use the s-convex combination in an another way. We will replace the convex combination in the iterations by the s-convex one. For instance, by introducing the s-convexity, the S-iteration takes the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} z_{n+1} = (1 - \alpha )^s B_m(z_n) + \alpha ^s B_m(v_n), \\ v_n = (1 - \beta )^s z_n + \beta ^s B_m(z_n), \end{array}\right. } \end{aligned}$$
(13)

where \(\alpha \in (0, 1]\), \(\beta \in [0, 1]\), and \(s \in (0, 1]\). Because for \(s = 1\), the s-convex combination reduces to the convex one, so for \(s = 1\), iteration (13) reduces to (10). Therefore, the introduction of an additional parameter into the S-iteration will give us more control on the dynamics of the underlying dynamical system.

4 Polynomiograph Generation

To generate a polynomiograph for our modified feedback process of the Basic Family of iterations, we use method presented in Algorithm 2. In this algorithm, we select a polynomial p, parameters \(\alpha \), \(\beta \), s for the S-iteration with s-convexity, and the number m of an element of the Basic Family of iterations. Then, for each starting point \(z_0\) in the area \(A \subset \mathbb {C}\) (the area is discretized depending on the resolution of the final image) we use (13) to iterate it. The iteration proceeds till the convergence test is satisfied [12]:

$$\begin{aligned} |z_{n+1} - z_n| < \varepsilon , \end{aligned}$$
(14)

where \(\varepsilon > 0\) is the accuracy of computations, or the maximum number of iterations is reached. Finally, when the iteration process ends, we determine a colour of the starting point \(z_0\). This can be done in may different ways. The two most popular methods of colouring are: basins of attraction and iteration colouring. In the basins of attraction colouring, each of the polynomial’s roots gets a distinct colour from the colour map colours. Then, if the number of performed iterations was less than N, then for the obtained root approximation \(z_{n+1}\), we search for the closest root and colour \(z_0\) with the colour of this root. If the number of performed iterations was equal to N, then we colour \(z_0\) with a colour other than any of the colours chosen for the roots. In the iteration colouring, we colour the starting point by mapping the number n of performed iterations on the colour in the colour map, i.e., we use colours[n].

figure b

5 Examples

In this section, some examples of the polynomiographs obtained by using the proposed S-iteration with s-convexity are presented. Moreover, plots presenting the dependence of the generation time (in seconds) of polynomiograph on the value of the s parameter in the s-convex combination are also presented.

In the examples, we used the \(B_3\) and \(B_4\) members of the Basic Family, and the other parameter were the following:

  1. 1.

    \(p_4(z) = z^4 + 4\), \(A = [-2, 2]^2\), \(N = 15\), \(\varepsilon = 0.001\), two sets of the S-iteration parameters: \(\alpha _1 = 0.2\), \(\beta _1 = 0.8\), and \(\alpha _2 = 0.7\), \(\beta _2 = 0.7\),

  2. 2.

    \(p_5(z) = z^5 + z\), \(A = [-2, 2]^2\), \(N = 15\), \(\varepsilon = 0.001\), two sets of the S-iteration parameters: \(\alpha _1 = 0.6\), \(\beta _1 = 0.85\), and \(\alpha _2 = 0.75\), \(\beta _2 = 0.35\).

The algorithm for polynomiograph’s generation was implemented in the Processing programming language. For the colouring, we selected the iteration colouring with the colour map presented in Fig. 1. The experiments were performed on a computer with the following specifications: Intel i5-4570 (@3.2 GHz) processor, 16 GB DDR3 RAM, and Microsoft Windows 10 (64-bit). The resolution of all polynomiographs was set to \(600 \times 600\) pixels and the step for the s parameter in the generation time experiments was equal to 0.01.

Fig. 1
figure 1

Colour map used in the examples

Full size image

5.1 Polynomial \(p_4(z) = z^4 + 4\)

We start this example with polynomiographs generated for \(p_4\) using Picard’s iteration—Fig. 2. In Fig. 2a, polynomiograph obtained with the \(B_3\) method (Halley’s method) is presented, whereas Fig. 2b presents polynomiograph generated by the \(B_4\) method. These two polynomiographs correspond to the original methods from the Basic Family of iterations.

Fig. 2
figure 2

Polynomiographs for \(p_4\) generated using Picard’s iteration and various root finding methods

Full size image

In Figs. 3 and 4, we see polynomiographs obtained with the modified \(B_3\) and \(B_4\) methods. We used the S-iteration with s-convexity in which \(\alpha _1 = 0.2\), and \(\beta _1 = 0.8\), and varying values of the s parameter were used. Comparing images from Fig. 2 with the ones in Figs. 3a and 4a, we see that the use of S-iteration (\(s = 1\) corresponds to the original S-iteration) alters the shape of polynomiographs. Not only the shape changes, but also the dynamics. In both cases, we see lower dynamics than in the case of Picard’s iteration. Introduction of the s-convexity in the S-iteration further alters the shape and dynamics of polynomiographs. In Fig. 3, we can observe that the most noticeable change of the shape is in the areas of Fig. 3a with the lowest dynamics. Together with the change of shape the dynamics also changes—the lower the value of s, the more dynamics can be observed. Moreover, looking at the colours in the polynomiographs we can infer that the number of iterations needed to find a root is increasing with the decrease of value of the s parameter. For the \(B_4\) method (Fig. 4), we see a very similar behaviour, but it is less noticeable. For instance, the shape difference between Fig. 4a, b is visible in the areas around the cross in the centre. In Fig. 4c, d, the shape changes not only around the cross, but also in other areas of the polynomiograph.

Fig. 3
figure 3

Polynomiographs for \(p_4\) generated using \(B_3\), S-iteration with \(\alpha _1 = 0.2\), \(\beta _1 = 0.8\) and varying s parameter

Full size image
Fig. 4
figure 4

Polynomiographs for \(p_4\) generated using \(B_4\), S-iteration with \(\alpha _1 = 0.2\), \(\beta _1 = 0.8\) and varying s parameter

Full size image

The generation times of polynomiographs obtained for the \(p_4\) polynomial using \(B_3\) and \(B_4\) root finding methods are presented in Fig. 5. From the plots, we see that both methods have a similar behaviour. For values of s close to 1.0, they obtain the shortest time—1.107 s for \(s = 0.91\) in the case of Halley’s methods and 1.157 s for \(s = 0.89\) in the case of \(B_4\) method. Then, the times are increasing as the value of s decreases, but the speed of change is different. For Halley’s method, the speed is faster than for the \(B_4\) method. For value of s equal to 0.21, the time for Halley’s method stops increasing and it stabilizes its value—it obtains a value of about 4.2 s. In case of the \(B_4\) method, the stabilization threshold is for a lower value of s, namely for \(s = 0.1\); the value of time is about 5.2 s. Moreover, we can observe that the generation times for high values of s, i.e., for \(s \in (0.72, 1]\), for the \(B_4\) method are greater than for Halley’s method. For \(s \in (0.12, 0.72)\), the situation is reversed, i.e., \(B_4\) method obtains shorter times than Halley’s method. And finally, for \(s \in (0, 0.12)\) we observe like for the high values of s that the times for Halley’s method are shorter than for the \(B_4\) method, but this time, the difference is bigger.

Fig. 5
figure 5

Dependence of the generation time (in seconds) on the value of the s parameter for \(p_4\) and the S-iteration with \(\alpha _1 = 0.2\), \(\beta _1 = 0.8\)

Full size image

Polynomiographs obtained for various values of s and the second set of parameters in the S-iteration, i.e., \(\alpha _2 = 0.7\), \(\beta _2 = 0.7\), are presented in Fig. 6 for the Halley’s method and in Fig. 7 for the \(B_4\) method. For \(s = 1\), presented in Figs. 6a, and 7a, we see polynomiographs obtained with the original S-iteration. Comparing these images with the ones obtained with the Picard iteration (Fig. 2), we see that the introduction of the S-iteration changes the shapes of polynomiographs and their dynamics. Similar to the first example, the dynamics in both cases is lower than for the Picard iteration. Now, by introducing the s parameter, we see a noticeable change in the shape of polynomiographs for the Halley’s method. For the \(B_4\) method, the change is smaller. In both cases, the biggest change is obtained in the areas of the lowest dynamics and the lowest values of the original iterations. The patterns obtained by Halley’s method look more interesting from the artistic point of view. Moreover, we can observe that the s parameter has great impact on the number of iterations performed by the root finding methods. The lower the value of s, the more iterations are needed to find the root.

Fig. 6
figure 6

Polynomiographs for \(p_4\) generated using \(B_3\), S-iteration with \(\alpha _2 = 0.7\), \(\beta _2 = 0.7\), and varying s parameter

Full size image
Fig. 7
figure 7

Polynomiographs for \(p_4\) generated using \(B_4\), S-iteration with \(\alpha _2 = 0.7\), \(\beta _2 = 0.7\), and varying s parameter

Full size image

In Fig. 8, plots, for the second example, showing the dependence of the generation time (in seconds) on the value of the s parameter are presented. The behaviour of both methods in this example is very similar to the behaviour from the first example. For high values of s, both methods obtain the shortest times—0.976 s for \(s = 0.93\) in the case of the Halley’s method, and for the \(B_4\) method 1.067 s for \(s = 0.96\). Then, for the decreasing values of s, the generation time is increasing. The time gets longer much faster for Halley’s method, and it stabilizes for this method for the s of about 0.25. In case of the \(B_4\) method, the stabilization is obtained for a lower value of s, i.e., \(s = 0.11\). Moreover, we can observe that for values of s between 0.13 and 0.78, the \(B_4\) method is faster than the Halley’s method, and that for the other values, the Halley method is faster except for the peak near \(s = 0.9\).

Fig. 8
figure 8

Dependence of the generation time (in seconds) on the value of the s parameter for \(p_4\) and the S-iteration with \(\alpha _2 = 0.7\), \(\beta _2 = 0.7\)

Full size image

5.2 Polynomial \(p_5(z) = z^5 + z\)

Similar to the \(p_4\) polynomial, we start the examples with polynomiographs generated using Picard’s iteration. In Fig. 9a, we see polynomiograph obtained with the \(B_3\) method, whereas in Fig. 9b, polynomiograph generated by the \(B_4\) method. These polynomiographs correspond to the original methods from the Basic Family of iterations.

Fig. 9
figure 9

Polynomiographs for \(p_5\) generated using Picard’s iteration and various root finding methods

Full size image

Polynomiographs for \(p_5\) obtained using the \(B_3\) and \(B_4\) methods are presented in Figs. 10 and 11, respectively. For their generation, the S-iteration with s-convexity with \(\alpha _1 = 0.6\), \(\beta _1 = 0.85\) and varying s was used. Comparing the polynomiographs from Fig. 9 with the ones in Figs. 10a and 11a, that correspond to the S-iteration without the s-convexity, we see that the shape of polynomiographs changes. For instance, the circular areas in the individual quarters change in blobs. The dynamics of the methods also has changed. In both cases, we can observe that the dynamics has decreased, similarly like for the \(p_4\) polynomial. The use of s-convexity in the S-iteration further changes both the shape of polynomiographs and the dynamics. In Fig. 10, we see that the biggest changes are appearing in areas in which in Fig. 10a, we see low dynamics besides the area around the root placed in 0. Around this root, we see small changes of the shape. From the polynomiographs, we see that the lower the value of s, the higher the dynamics. Moreover, we can observe that the number of iterations needed for finding the root is increasing in areas in which the dynamics is increasing. For the \(B_4\) (Fig. 11), we see a very similar behaviour, but the changes are not so clear as in the case of the \(B_3\) method. For value near 1, we need to closely look at the polynomiographs to observe the places in which the shape changes. With the decrease of value of the s parameter, the changes are more sharp.

Fig. 10
figure 10

Polynomiographs for \(p_5\) generated using \(B_3\), S-iteration with \(\alpha _1 = 0.6\), \(\beta _1 = 0.85\), and varying s parameter

Full size image
Fig. 11
figure 11

Polynomiographs for \(p_5\) generated using \(B_4\), S-iteration with \(\alpha _1 = 0.6\), \(\beta _1 = 0.85\), and varying s parameter

Full size image

Generation times (in seconds) for the \(p_5\) polynomial and the \(B_3\) and \(B_4\) methods are presented in Fig. 12. From the plots, we see that both methods behave very similarly. The overall trend is that with the decrease of the s parameter, the generation time is increasing. Therefore, both methods obtain the shortest times near \(s = 1\), i.e., 1.262 s for \(s = 0.95\) in the case of the \(B_3\) method and 1.32 s for \(s = 0.99\) in the case of the \(B_4\) method. For \(s \in (0.5, 1)\), the times for both methods are similar. Below 0.5, we see that the times increase with different speed. The time for the \(B_3\) method is increasing faster for \(s \in (0.21, 0.5)\), and for \(s \in (0, 0.21)\), the \(B_4\) methods need more time for polynomiograph’s generation.

Fig. 12
figure 12

Dependence of the generation time (in seconds) on the value of the s parameter for \(p_5\) and the S-iteration with \(\alpha _1 = 0.6\), \(\beta _1 = 0.85\)

Full size image

Examples obtained for the second set of parameters in the S-iteration (\(\alpha _2 = 0.75\), \(\beta _2 = 0.35\)) for the \(B_3\) and \(B_4\) methods are presented in Figs. 13 and 14, respectively. Similarly like in the previous examples, in Figs. 13a and 14a, we see polynomiographs obtained for \(s = 1\) that is with the help of the standard S-iteration. Comparing these images with the ones generated for the Picard iteration (Fig. 9), we see that in both cases, the polynomiographs differ in both the shape and dynamics. The dynamics is lower than in the case of Picard’s iteration, especially in case of the \(B_4\) method. For \(s < 1\), we introduce the s-convexity into the S-iteration (Figs. 13b–d, 14b–d). Similarly like in the case of the first set of parameters, the shape and the dynamics change in the areas, wherein Figs. 13a and 14a, we saw low dynamics except for the area around 0. The more interesting change in shape and colour can be observed in case of the \(B_3\) method.

Fig. 13
figure 13

Polynomiographs for \(p_5\) generated using \(B_3\), S-iteration with \(\alpha _2 = 0.75\), \(\beta _2 = 0.35\), and varying s parameter

Full size image
Fig. 14
figure 14

Polynomiographs for \(p_5\) generated using \(B_4\), S-iteration with \(\alpha _2 = 0.75\), \(\beta _2 = 0.35\), and varying s parameter

Full size image

In Fig. 15, plots of the generation times (in seconds) for various values of s are presented. Similarly like in all the previous examples, we see a very similar dependency. For high values of s, we obtain the shortest times, and when the value of s is decreasing, then the time for both methods is increasing. The shortest time (1.27 s) Halley’s method obtained for \(s = 0.99\), and the \(B_4\) method obtained the shortest time (1.369 s) for \(s = 0.98\). Moreover, we see again that for the high values of s, both methods obtain comparable times; next, the Halley’s method is slower than the \(B_4\) method; and that for the low values of s, the situation changes and the \(B_4\) method is slower. The longest time (4.721 s) Halley’s method obtained for \(s = 0.15\), whereas the \(B_4\) method its longest time (6.077 s) obtained for \(s = 0.13\).

Fig. 15
figure 15

Dependence of the generation time (in seconds) on the value of the s parameter for \(p_5\) and the S-iteration with \(\alpha _2 = 0.75\) and \(\beta _2 = 0.35\)

Full size image

6 Conclusions

In this paper, we presented the concept of the use of s-convex combination in various iteration processes from fixed point theory. We used this modified iteration schemes to replace Picard’s iteration in the root finding methods from the Basic Family of iterations. Furthermore, we presented graphical examples in form of polynomiographs and numerical examples showing the dependence of the generation time on the value of the s parameters. In the examples, we used only the S-iteration. The presented graphical examples showed that the use of s-convex combination can change both the shape and the dynamics of the root finding methods. Moreover, the numerical examples showed that the value of the s parameter has great impact on the generation time—the lower its value, the longer the time.