Direct Linear Interpolation of Geometric Objects in Conformal Geometric Algebra

Abstract

Typically we do not add objects in conformal geometric algebra (CGA), rather we apply operations that preserve grade, usually via rotors, such as rotation, translation, dilation, or via reflection and inversion. However, here we show that direct linear interpolation of conformal geometric objects can be both intuitive and of practical use. We present a method that generates useful interpolations of point pairs, lines, circles, planes and spheres and describe algorithms and proofs of interest for computer vision applications that use this direct averaging of geometric objects.

1 Introduction

In this paper we will look at adding CGA objects and adjusting the resulting multivectors to produce useful interpolations of the objects. We will present a general technique that is valid for all geometric objects of grade 2 or above. This technique uses the decompositions presented in [6].

The objects we work with here will be CGA objects unless explicitly stated otherwise. We will use the standard extension of the 3D geometric algebra, where our 5D CGA space is made up of the standard spatial basis vectors $\{e_i\}$ $i=1,2,3$, plus two additional basis vectors, e and ${\bar{e}}$ with signatures, $e^2=1$, ${\bar{e}}^2=-1$. Two null vectors can therefore be defined as: $n_{\infty }=e + {\bar{e}}$ and $n_0 = \frac{e - {\bar{e}}}{2}$. The mapping of a 3D vector x to its conformal representation X is given by $X = F(x) = \frac{1}{2}(x^2 n_{\infty } + 2x - 2n_0)$.¹

2 Motivation

In our conformal representation of space the blades of a given grade n represent specific classes of object and lie on a manifold within the overall subspace of grade n. Typically in geometric algebra we traverse this manifold using rotors and reflections. These transformations are incredibly useful and make up the vast majority of operations used in the field of applied geometric algebra. Unfortunately, while being of geometric significance, rotors and reflections are often unintuitive ways of thinking about a problem and traditional algorithms often require significant rehashing to put within this framework.

For example: given a cluster of geometric objects we would like to be able to create an ‘average’ object that lies in some sense in the middle of the bundle. Most geometric algebra approaches to this problem would likely require the explicit design of a geometrically motivated cost function followed by constrained optimisation on the blade manifold either directly or via a parametrisation of rotors over the space.

While this approach has been very effective for a variety of problems, it requires the careful crafting of clever cost functions, consideration of the convexity of the underlying space, efficient implementation of the given optimisation scheme etc. The question we aim to answer here is: what if we just decided to add all the objects together?

3 Linearly Interpolating Conformal Points

The result of linear combinations of conformal points is well known [12]. Consider two arbitrary points in 3d space a and b represented as A and B in our conformal model. Linear interpolation of these points followed by our conformal mapping produces a linear interpolation of our conformal points with an additional term in $n_{\infty }$:

$$\begin{aligned} F( \alpha a + (1-\alpha ) b ) = \alpha A + (1-\alpha ) B + \alpha (1-\alpha )(A\cdot B)n_{\infty } \end{aligned}$$

(1)

We can therefore get a useful interpolation of points by taking a direct linear interpolation and simply adding the final $\alpha (1-\alpha )(A\cdot B)n_{\infty }$ term to the result. If $Y= \alpha A + (1-\alpha ) B$, we can recover $Y' = F( \alpha a + (1-\alpha ) b )$ via the following formula (assuming $Y'\cdot n_{\infty }=-1$):

$$\begin{aligned} Y' = \frac{-Yn_{\infty }Y}{2(Y\cdot n_{\infty })^2} \end{aligned}$$

4 Linearly Interpolating Higher Grade Conformal Objects

Objects of grade 2 and above are more difficult to interpolate in a sensible and computationally efficient way. Typically, schemes that have been found are either only valid for certain objects in specific cases [4], or the problem is attacked indirectly via carriers [9] or by forming the rotor between the objects, extracting the corresponding bivector, which is then interpolated [15] and applied to the first object.

It is shown in [11] that we can represent the mirror object $X_m$ that reflects one object $X_1$, into another $X_2$, as the left multiplication of the summation of the blades by a scalar + 4-vector factor S:

$$\begin{aligned} X_m = S(X_1 + X_2) = (\beta + \gamma (X_1X_2 + X_2X_1))(X_1 + X_2) \end{aligned}$$

(2)

where $\beta$ and $\gamma$ are scalars and the 4-vector part of S is proportional to the anticommutator of $X_1$ and $X_2$.

For the previously known cases in which the linear interpolation of higher grade objects gives a blade, such as with circles [4] and point pairs [5] both with common points, the factor S is a scalar and the object $X_m$ is simply ‘half-way’ between the objects. We can extend this notion to the cases where the addition of objects is not a blade by using our object $X_m$, which has been corrected to being a blade, as the half-way object. We can use this idea of the half-way object to recursively subdivide the space between $X_1$ and $X_2$ allowing us to create objects that are any fraction of $X_1$ and $X_2$. While this technique allows us to generate interpolant objects from any two objects (of the same type), it is nevertheless clumsy to represent fractional interpolant objects via repeated subdivision. This subdivision technique also provides no obvious way of performing an average of many objects. What we would really like is some way of directly dealing with the linear interpolation $\alpha X_1 + (1-\alpha ) X_2$.

5 Creating a Blade from a Pure Grade Multivector

Consider the general interpolant, $X_{\alpha }' = \alpha X_1 + (1-\alpha )X_2$ where $X_1$ and $X_2$ are blades of the same grade. We claim that we can project $X_{\alpha }'$ into object space in a simple and general way. First we will generalise Eq. (2) to the interpolation case:

$$\begin{aligned} X_\alpha = S(\alpha X_1 + (1-\alpha )X_2) = (\beta _\alpha + \gamma _\alpha (X_1X_2 + X_2X_1))(\alpha X_1 + (1-\alpha )X_2) \end{aligned}$$

(3)

where $\beta _\alpha$ and $\gamma _\alpha$ are once again scalars.

Since S is of the form (scalar + 4-vector) it is self reverse. Defining $S^- = \langle S \rangle _0 - \langle S \rangle _4$ we get the result that $S^-S$ is a scalar, and can therefore write $X'_\alpha = k S^- X_\alpha$ where k is a scalar and $k = \frac{1}{S^-S}$.

To use this decomposition we need to extract S from $X'_\alpha$. To do this we can use the methods of [11], or as follows using the square root operator of Dorst and Valkenburg [6].

Let $SX'_\alpha = X_\alpha$, where $X_\alpha$ is a valid object (squaring to ± 1). Now define $\Sigma \in Cl^{0,4}_{4,1}$, ie. it only contains 0 and 4 grade coefficients and is an element of the conformal algebra. Then, defining $[[\Sigma ]] = \sqrt{\langle {\Sigma }\rangle _0^2 - \langle {\Sigma }\rangle _4^2}$, the square root can be found as:

$$\begin{aligned} \sqrt{\Sigma } = \frac{\Sigma \pm [[\Sigma ]]}{\sqrt{2}\sqrt{\langle {\Sigma }\rangle _0 \pm [[\Sigma ]]}} = \frac{\langle \Sigma \rangle _0 \pm [[\Sigma ]]}{\sqrt{2}\sqrt{\langle {\Sigma }\rangle _0 \pm [[\Sigma ]]}} + \frac{\langle {\Sigma }\rangle _4}{\sqrt{2}\sqrt{\langle {\Sigma }\rangle _0 \pm [[\Sigma ]]}} \end{aligned}$$

(4)

To use this method to find $S^-$ we multiply our non-blade object by its own reverse:

$$\begin{aligned} X'_\alpha {\tilde{X}}'_\alpha {=} (kS^-X_\alpha )(kS^-X_\alpha )\,\tilde{} {=} k^2S^-X_\alpha {\tilde{X}}_\alpha (S^-)\,\tilde{} = -k^2S^-(S^-)\,\tilde{} {=} -k^2(S^-)^2 \end{aligned}$$

(5)

this is now in a form where we can apply the above square root formula:

$$\begin{aligned} kS^- = \sqrt{-X'_\alpha {\tilde{X}}'_\alpha } \end{aligned}$$

(6)

it now simply remains to isolate $X_\alpha$ via multiplication by kS where $kS = \langle kS^- \rangle _0 - \langle kS^- \rangle _4$. Since $(kS)(kS^-)$ is a scalar, we have

$$\begin{aligned} X_\alpha = \frac{kS}{(kS)(kS^-)} X'_\alpha \equiv SX'_\alpha \end{aligned}$$

(7)

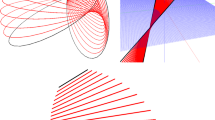
This result is particularly important as we have identified a way of projecting any pure grade object of the form $S^-X$ (with X a blade) back to the blade manifold. An immediate application of this is that we can now deal with arbitrary linear combinations of objects, allowing us to smoothly interpolate as well as to average and cluster geometric primitives. Additionally we can correct numerical errors that result from arithmetic operations to give true blades again. Figure 1 shows examples of interpolating various geometric objects.

As shown in [11] this method holds for all the standard normalised conformal objects of grade 2 or above (point pairs, lines, circles, planes, spheres). The direct interpolation method is potentially more computationally efficient than the bivector interpolation method, and its form indicates that it is covariant, ie, for a rotor transformation given by R,

$$\begin{aligned} R[\alpha X_1 + (1-\alpha )X_2]{\tilde{R}} = \alpha RX_1{\tilde{R}} + (1-\alpha )RX_2{\tilde{R}} \end{aligned}$$

Unfortunately, we cannot apply this form of interpolation to points as we encounter a problem due to the fact that for a conformal point P, $P{{\tilde{P}}} = 0$. However, we saw in Eq. (1) that points can be interpolated very easily using known explicit formulae.

Fig. 1

Linear interpolation between different geometric objects. a Circles, b point pairs, c planes, d spheres. The pure red and green objects here represent $X_1$ and $X_2$ and the intermediate colours show the interpolations between them. Here we are stepping linearly through $\alpha$ between 0 and 1 with the number of steps chosen to show the interpolations as clearly as possible

6 Techniques for Understanding Interpolant Properties

In order to use the interpolant blades it is useful to get a handle on some of their properties. In several cases it is possible to get good insight into how the interpolant behaves by looking at the interpolant of the dual of the blades, but in others we need to consider the form of the (scalar + 4-vector) required to project the interpolant back to the blade manifold. As before we write our blades as:

$$\begin{aligned} X_\alpha = (\langle S\rangle _0 + \langle S\rangle _4)(\alpha X_1 + (1-\alpha ) X_2) \end{aligned}$$

From this we immediately see that for the multiplication to be grade preserving we require $\langle S\rangle _4X_1$ and $\langle S\rangle _4 X_2$ to give only objects of grade n where n is the grade of $X_1$ and $X_2$. Table 1 shows the resultant grades from the geometric product of pure grade objects and Table 2 shows the resultant grades from the inner product. These tables are presented here for reference and will be returned to when dealing with individual grade blades.

Table 1 Resulting grades from the geometric product of pure grade objects

Table 2 Resulting grades from theinner product of pure grade objects

7 Point Pairs

We start with point pairs. Previous work [5] has shown that when an end point is shared between point pairs A and B the interpolant point pairs are also blades and their end points trace out the circumference of the circle formed by the shared point and the additional separate end points. Three points X, Y, Z define a circle $C \propto X\wedge Y \wedge Z$ and a fourth point V lying on the circle will satisfy $V\wedge C = 0$ , this allows us to define a check to see if two point pairs are chords of the same circle. Point pairs $A = V\wedge X$, $B = Y\wedge Z$ will satisfy $A\wedge B = 0$ if they are both chords and any additional chord, W, of the same circle will satisfy $W\wedge A = 0, W\wedge B = 0$ and thus $W\wedge (A + B) = 0$. This leads to:

Theorem 1

If point pairs A and B are both chords of a common circle C the interpolant point pairs $T \propto \alpha A + (1-\alpha )B$ are blades and also have end points lying on C as $\langle AB\rangle _4=A\wedge B=0$ and $(\alpha A + (1-\alpha )B)\wedge (A + B) = 0$.

Note, since $\langle AB\rangle _4=A\wedge B=0$, the projector S is a scalar. The common circle itself is the ‘join’ of the two original point pairs and can be computed with the algorithms supplied in Chapter 21 of Dorst, Fontijne and Mann [5]. Figure 2 shows two cases of the interpolation of co-planar point pairs that lie on the same circle.

Fig. 2

The interpolation of point pairs with endpoints lying in the same plane and on a common circle is a blade and also lies on the same common circle, even in cases in which there are no shared endpoints or intersections. In this figure the red lines are the interpolation of the black lines

Fig. 3

The interpolation in red of point pairs A and B, here shown in black, lie on the surface of the sphere $\propto A\wedge B$, shown in blue with black equator circle

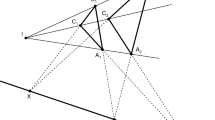
Turing to the more general case of two point pairs in arbitrary positions in space we can get insight into the form of the interpolant by considering the components of the scalar + 4-vector projection factor. In the case of the geometric product between grade 4 and grade 2 objects we see from Table 1 that we produce both 2 and 4-vector grades. The 2-vector part of the geometric product comes from the inner product between the point pairs and the 4-vector. ie. for point pairs A and B, $\langle S\rangle _4(\alpha A + (1- \alpha )B) = \langle S\rangle _4\cdot (\alpha A + (1- \alpha )B)$. For the general case of two point pairs not lying in plane ie. $A \wedge B \ne 0$, we can show that there is only one object that behaves in this way, the sphere $\Sigma \propto A\wedge B$, as it passes through both end points of both point pairs. This is illustrated in Fig. 3 and suggests that the sphere $\Sigma$ is intrinsically tied to the form of the interpolant objects. Indeed we can see from the same visualisation that the interpolant C of point pairs A and B always has endpoints lying on the surface of the sphere $\Sigma$.

We can prove this by showing that $C\wedge B$ or $C\wedge A$ also produces the sphere:

$$\begin{aligned} \Sigma&\propto A\wedge B \end{aligned}$$

First consider an interpolant object C and its outer product with one of the original objects, B

$$\begin{aligned} C&= (\langle S\rangle _0 + \langle S\rangle _4)(\alpha A + (1-\alpha )B)\\ C\wedge B&= ((\langle S\rangle _0 + \langle S\rangle _4)(\alpha A + (1-\alpha )B))\wedge B\\&= \langle S\rangle _0(\alpha A + (1-\alpha )B)\wedge B + (\langle S\rangle _4(\alpha A + (1-\alpha )B))\wedge B \end{aligned}$$

as $B\wedge B = 0$ we see that

$$\begin{aligned} \alpha \langle S\rangle _0 A\wedge B = \langle S\rangle _0(\alpha A + (1-\alpha )B)\wedge B \end{aligned}$$

Now we just need to prove that $\langle S\rangle _4((\alpha A + (1-\alpha )B)\wedge B)$ is a scalar multiple of $A\wedge B$. From Eq. (3) we know that

$$\begin{aligned} \langle S\rangle _4 \propto \langle AB + BA \rangle _4 \end{aligned}$$

it is therefore sufficient to prove that:

$$\begin{aligned} T&= (\langle AB + BA \rangle _4(\alpha A + (1-\alpha )B))\wedge B \propto A\wedge B \end{aligned}$$

We can convert the outer product into a geometric product followed by a projection and thus can write:

$$\begin{aligned} T&= \langle \langle AB + BA \rangle _4(\alpha A + (1-\alpha )B)B\rangle _4 \\&= \langle \langle AB + BA \rangle _4(\alpha AB + (1-\alpha ))\rangle _4 \\&= (1-\alpha )(\langle AB\rangle _4 + \langle BA \rangle _4) + \alpha \langle (\langle AB\rangle _4 + \langle BA \rangle _4)AB\rangle _4 \end{aligned}$$

As $\langle AB\rangle _4 \equiv \langle BA\rangle _4$ we can write this as:

$$\begin{aligned} T = 2 (1-\alpha )\langle AB\rangle _4 + 2\alpha \langle \langle AB\rangle _4 AB\rangle _4 \end{aligned}$$

and this can further simplified using the fact that:

$$\begin{aligned} \langle \langle AB\rangle _4 AB\rangle _4 = \langle \langle AB\rangle _4 \langle AB\rangle _0 \rangle _4 \end{aligned}$$

As $\langle AB\rangle _0 = A\cdot B$ is a scalar:

$$\begin{aligned} T&= 2(1-\alpha )\langle AB\rangle _4 + 2\alpha \langle AB\rangle _4 (A \cdot B) \\&= 2((1-\alpha ) + \alpha A \cdot B)\langle AB\rangle _4 \end{aligned}$$

As $2((1-\alpha ) + \alpha A \cdot B)$ is a scalar we see that the proof is completed

$$\begin{aligned} 2((1-\alpha ) + \alpha A \cdot B)\langle AB\rangle _4 \propto \langle AB\rangle _4 \equiv A\wedge B \end{aligned}$$

Figure 3 shows a graphical representation of the interpolant point pairs lying on the surface of the sphere. To summarise:

Theorem 2

For non-coplanar point pairs A and B, all interpolant point pairs lie on the surface of the sphere $\Sigma \propto A\wedge B$.

8 Circles

The interpolant of circles has a range of properties that are useful and clearly intrinsically tied to the geometry of spheres and point pairs. Initially we will consider the case of two circles in space that both lie on the surface of a common sphere. In past work it has been shown that circles with two common points interpolate directly without requiring re-projection and the interpolant lies on their common sphere [4, 5]. Here, as with the point pairs, we can show that this is true for a broader class of circles:

Theorem 3

If circles $C_1$ and $C_2$ together define the caps of a common sphere then $\langle S\rangle _4 \propto \langle C_1C_2 \rangle _4 = 0$ where S is of the form shown in Eq. (3) and thus any interpolant object $C_3 = \alpha C_1 + (1-\alpha )C_2$ is a blade without requiring re-projection to the blade manifold.

This can be proved by considering each circle $C_i$ as the intersection of a plane $P_i$ and a sphere $\Sigma _i$. Forming this intersection via the dual (where $X^* = XI_5$ and $I_5$ is the 5D space pseudoscalar), we have:

$$\begin{aligned} C_1&= (\Sigma _1^*\wedge P_1^*)I_5 \\ C_2&= (\Sigma _2^*\wedge P_2^*)I_5 \\ \langle C_1C_2\rangle _4&= -\langle (\Sigma _1^*\wedge P_1^*)(\Sigma _2^*\wedge P_2^*)\rangle _4 \end{aligned}$$

Since $(\Sigma _1^*\wedge P_1^*)$ and $(\Sigma _2^*\wedge P_2^*)$ are both bivectors:

$$\begin{aligned} \langle C_1C_2\rangle _4 = -\Sigma _1^*\wedge P_1^*\wedge \Sigma _2^*\wedge P_2^* \end{aligned}$$

and so if $\Sigma _2 \propto \Sigma _1$:

$$\begin{aligned} \langle C_1C_2\rangle _4 \propto -\Sigma _1^*\wedge P_1^*\wedge \Sigma _1^*\wedge P_2^* = 0 \end{aligned}$$

We can additionally find the unique common sphere by finding the join of the circles or by reverting to linear algebra techniques:

Conjecture 1

If circles $C_1$ and $C_2$ together define the caps of a common sphere $\Sigma$ then $\langle C_1 \Sigma \rangle _3, \langle C_2 \Sigma \rangle _3 = 0$. $\Sigma$ can be found by the following process:

First we define:

where $M_3$ is the truncated identity matrix that performs selection of grade 3 elements from a vector of coefficients and and are the matrices that perform the left geometric product of $C_1$ and $C_2$ respectively with a vector of coefficients. We can then find the $\Sigma$ for where is a vector of canonical blade coefficients limited to only the 4-vector blades. In the case that $C_1$ and $C_2$ are the same radius then $\Sigma \propto (C_1 + C_2)((C_1 + C_2)\wedge n_{\infty })I_5$.

The case for circles of the same radius is visualised in Fig. 4.

It is also the case that the interpolant lies on the surface of the common sphere:

Theorem 4

If circles $C_1$ and $C_2$ together define the caps of a common sphere then all interpolant circles $C_3 = \alpha C_1 + (1-\alpha )C_2$ (which we have shown to be blades) also lie on the surface of the sphere $\Sigma$ common to both.

We can prove this by considering the outer product of the interpolant circle with D, an arbitrary point on the common sphere $\Sigma$:

$$\begin{aligned} \Sigma \propto D\wedge C_3 = \alpha D\wedge C_1 + (1-\alpha )D\wedge C_2 \end{aligned}$$

Figure 5 shows an example of this interpolation.

Fig. 4

The half way circle $C_1 + C_2$ shown in red in this figure is the equator of the sphere through both $C_1$ and $C_2$ if they define a common sphere and have the same radius

Fig. 5

The interpolation of circles $C_1$ and $C_2$ is a blade and lies on the surface of a sphere if $C_1$ and $C_2$ define a common sphere

Thus far we have dealt exclusively with circles on a common sphere. In the case in which $C_1$ and $C_2$ do not lie on the same sphere we can again look at how the interpolants behave by considering the form of the (scalar + 4-vector) that we use to project the interpolant back to the blade manifold. In the case of the geometric product between grade 4 and 3 objects we see from Table 1 that we produce both 1 and 3-vector grades, however the 1-vector part of the geometric product comes only from the inner product between the 4-vector and the circles. To maintain grade after the multiplication the 4-vector must therefore be the object that has an inner product of zero with both circles. This object is the sphere into whose surface both circles plunge orthogonally [5]:

Theorem 5

If circles $C_1$ and $C_2$ together do not lie on a common sphere then the 4-vector from our blade projection equation $\langle S\rangle _4 \propto \langle C_1C_2 \rangle _4$ is itself a blade and geometrically represents the sphere through which both circles plunge orthogonally. ie. $C_1\cdot \langle C_1C_2 \rangle _4 = 0$. This property means all interpolant circles after projection to the blade manifold also plunge through $\langle C_1C_2 \rangle _4$ orthogonally. ie. $C_3\cdot \langle C_1C_2 \rangle _4 = 0$.

The intersections of the interpolant circles with the sphere $\langle S\rangle _4$ produce a set of point pairs. Intuition would suggest that these point pairs have properties tied to the interpolation of the point pairs generated by the original two circles $C_1$ and $C_2$ and indeed we can numerically verify that this is the case:

Conjecture 2

If circles $C_1$ and $C_2$ together do not lie on a common sphere then the intersection point pair $P_\alpha$ formed by the meet of the circle interpolant for a given value of $\alpha$ with the orthogonal sphere $\langle C_1C_2 \rangle _4$ ie. $P_\alpha \propto C_\alpha \vee \langle C_1C_2 \rangle _4$ is the same as the re-projected interpolant $\Pi _\alpha$ of the point pairs formed from the meet of $C_1$ and $C_2$ with $\langle C_1C_2 \rangle _4$.

Figure 6 shows the interpolation of two non co-spherical circles as well as the sphere these circles define and the intersection point pairs they generate.

Fig. 6

The interpolation of the two black circles which are not spherical caps, intersect orthogonally with a single sphere (shown in blue). The point pairs formed from the two intersection points are shown in yellow

9 Lines

When looking at lines we can attempt to use some of the same techniques that we used for circles. First consider the form of $\langle S\rangle _4 \propto \langle L_1L_2\rangle _4$. For lines $\langle L_1L_2\rangle _4 \propto I_5n_{\infty }$, giving the form of the projection of $(X_1 + X_2)$ as:

$$\begin{aligned} X_3 = (\mu + \nu I_5n_{\infty })(X_1 + X_2) \end{aligned}$$

(8)

where $\mu$ and $\nu$ are scalars. While neat, this form $I_5n_{\infty }$ does not on its own provide information on the properties of the interpolated line. Instead we consider the interpolation of the dual of the lines, and to understand this interpolation we must take a short detour via screw theory.

9.1 Screw Theory

Screw theory was developed by Sir Robert Stawell Ball in 1900 in his seminal work ‘A treatise on the theory of screws’ [1]. His original applications were kinematics and one of the most important theorems in the area, Chasles’ theorem, states that the most general rigid body displacement can be described by a screw transformation. More recently screw theory, and the highly related study of dual quaternions, has been applied to robotics, computational geometry and multibody dynamics [3, 10, 13].

Screw transformations consist of a translation along an axis and a rotation around that axis. To parameterise a screw we define the direction of the screw axis via a unit vector ${\hat{m}}$, a point on the screw axis p and a screw pitch h. The pitch represents how far to move in the direction of the screw axis for each complete revolution about the axis.

9.2 Bivector Representation of a Line

A line in CGA is represented as a 3-vector, or dually as a bivector:

$$\begin{aligned} L^* = {\hat{m}} I_3 + (p\wedge {\hat{m}})I_3 n_{\infty } \end{aligned}$$

(9)

This bivector formulation is equivalent to the Plücker coordinates of the line.

In [6] the authors describe the orbit of simple bivectors that describe motion. We can visualise the orbit of the dual line bivector by exponentiating the bivector to a rotor and applying it to a test point. Figure 7 shows the orbit of the point at the origin about a line. The motion is a circle about the line.

Fig. 7

The orbit of a line

9.3 The Bivector Representation of a Screw

To represent a screw we will couple the rotational motion of the dual of a line with a translation in the direction of that same line. The bivector T that transforms along the 3D vector t is:

$$\begin{aligned} T = tn_{\infty } \end{aligned}$$

(10)

If $t = h {\hat{m}}$ where h is a scalar, ie. the translation is in the screw axis direction, the rotors formed from the bivectors in Eqs. (9) and (10) commute.

It then follows that the rotor formed from the addition of the bivectors in Eqs. (9) and (10) can be split into the rotor representing translation along the axis and the rotor representing rotation about the axis—as required for a screw. We therefore have a screw, $\mathbb {S}$, whose action on the point at the origin is shown in Fig. 8.

$$\begin{aligned} \mathbb {S} = {\hat{m}} I_3 + (p\wedge {\hat{m}})I_3 n_{\infty }+ h{\hat{m}}n_{\infty } \end{aligned}$$

(11)

Fig. 8

The action of a basic screw formed by the summation of commuting bivectors applied to the point at the origin is shown in black, it forms a screw motion about the screw axis shown in red

Hestenes and Sobczyk [8] p81 gives an expression for decomposing any bivector into two commuting blades. In the case of our screw bivector these blades represent the dual of the screw axis $L^*$ and a translational bivector T in the direction of the screw axis. ie. given a screw bivector $\mathbb {S}$ we can decompose it as:

$$\begin{aligned} \mathbb {S} = L^* + T \end{aligned}$$

9.4 Adding Dual Lines

The addition of dual lines produces a bivector. Visualising the action of this bivector allows us to see that it is in fact also a screw transformation. Consider the addition of two dual lines:

$$\begin{aligned} L^*_+ = L_1^* + L_2^* \end{aligned}$$

we can write this elementwise as

$$\begin{aligned} L^*_+ = m_1I_3 + \psi _1 n_{\infty }+ m_2I_3 + \psi _2 n_{\infty }\end{aligned}$$

where $\psi _i$ is $(p_i\wedge m_i)I_3$. We then rearrange to give something proportional to the expression in Eq. (11):

$$\begin{aligned} L^*_+&= (m_1+ m_2 )I_3 + (\psi _1 + \psi _2 )n_{\infty }= m I_3 + (p\wedge m)I_3 n_{\infty }+ hmn_{\infty }\end{aligned}$$

Where clearly $m = m_1 + m_2$. If we divide this by |m| we have the general form of a normalised screw

$$\begin{aligned} \mathbb {S} = {\hat{m}} I_3 + (p\wedge {\hat{m}})I_3 n_{\infty }+ h{\hat{m}}n_{\infty }\end{aligned}$$

Gathering like terms, specifically those without an $n_{\infty }$ component, leads us to the conclusion that our screw axis direction ${\hat{m}}$ must simply be proportional to the addition of the directions of the two lines. Using this fixed axis direction we can extract the coefficient h (the pitch) of the translation bivector parallel to the screw axis:

$$\begin{aligned} m&= m_1 + m_2\\ L_+^*&= m I_3 + (p\wedge m)I_3 n_{\infty }+ hmn_{\infty }\\ L_+^*\cdot n_0&= hm + (p\wedge m)I_3 \\ h&= \frac{(L_+^*\cdot n_0) \cdot m}{|m|^2} \end{aligned}$$

With this coefficient known we now have all the pieces in place for a full decomposition of the dual line addition bivector $L_+^*$:

$$\begin{aligned} L_+^*&= L_1^* + L_2^* \\ m&= -\langle L_+^* \rangle _{(e_{12},e_{13},e_{23})}I_3\\ h&= \left( \frac{(L_+^*\cdot n_0) \cdot m}{|m|^2}\right) \\ \mathbb {S}&= L^* + T \\ T&= h\,{\hat{m}}n_{\infty }\\ L^*&= \mathbb {S} - T \end{aligned}$$

Figure 9 shows the decomposition of the addition of two lines into its component parts.

Fig. 9

The addition of two dual lines, here shown in black, produces a screw, whose action on the point at the origin is again shown in black. The screw can be decomposed into two commuting bivectors, whose actions are shown in red and blue. The bivector whose action is shown in red is the dual of the screw axis line, also shown in red

9.5 Relationship to Object Manifold Reprojection

We can also analyse the screw multiplied by its own reverse, comparing this formulation with our object manifold reprojection to get the projection coefficient S in terms of the screw parameters:

$$\begin{aligned} {\mathbb {S}}\tilde{\mathbb {S}}&= -(L^*)^2 + T{\tilde{T}} + T\tilde{L^*} + L^*{\tilde{T}} \\&= 1 - 2TL^* \\&= 1 + 2hn_{\infty }I_3 = 1 + 2hI_5n_{\infty }\\&\equiv (kS^-)^2 \\ (kS^-)&= \mu + \nu I_5 n_{\infty }\\ (kS^-)^2&= \mu ^2 + 2\mu \nu I_5 n_{\infty }\\ \mu&= 1, \,\,\, \nu = h \end{aligned}$$

Using this calculated value we can see how the projection coefficient acts on the addition of lines:

$$\begin{aligned} L^* \propto&(1 - h I_5 n_{\infty })(m I_3 + (p\wedge m)I_3 n_{\infty }+ hmn_{\infty })\\&= m I_3 + (p\wedge m)I_3 n_{\infty }+ hmn_{\infty }- hmn_{\infty }\\&= m I_3 + (p\wedge m)I_3 n_{\infty }\end{aligned}$$

This is in fact the same line as is formed from the decomposition of the screw bivector into the screw axis bivector and pitch translation bivector. In other words, the addition of lines and reprojection to the line manifold extracts the axis of the screw formed from the addition of their duals. This axis has a direction equal to a linear interpolation of the axes of the original two lines and, as it is a mirror object, passes through the point exactly half way between the lines.

10 Planes

All 4-vectors are blades. Thus, for planes and spheres it is impossible to construct an invalid geometric object by addition. For planes we can analyse the form of the interpolant by again looking at the dual of a plane.

The dual of the plane can be written as:

$$\begin{aligned} P^* = {\hat{m}} + dn_{\infty }\end{aligned}$$

where ${\hat{m}}$ is the 3d vector normal to the plane and d is the perpendicular distance of the plane from the origin. Thus the interpolation of duals of two planes can be written as:

$$\begin{aligned} \alpha P_1^* + (1-\alpha )P_2^*= \alpha \hat{m_1} + \alpha d_1n_{\infty }+ (1-\alpha )\hat{m_2} + (1-\alpha )d_2n_{\infty }\end{aligned}$$

which, when we collect like terms, is already in the form of a dual plane $P_3^*$:

$$\begin{aligned} P_3^* = \alpha \hat{m_1} + (1-\alpha )\hat{m_2} + (\alpha d_1 + (1-\alpha )d_2)n_{\infty }\end{aligned}$$

(12)

this dual plane has a normal vector that is the interpolation of the normal vectors of the original two planes and has a perpendicular distance from the origin that is also simply an interpolation of the perpendicular distance from the origin of the original two planes. An important feature of this plane interpolation is that, as noted in [2], provided the two planes intersect, the interpolant plane always passes through the line of intersection (the meet) of the two original planes. This is visualised in Fig. 10. In the case that the planes to not intersect (or more formally are said to intersect at infinity) the interpolation will smoothly translate one plane to the other keeping the normal fixed, the parallel vs anti-parallel cases are explored in Figs. 11 and 12.

Fig. 10

The interpolant of two planes (green to red) always passes through the meet line (black) of the two original planes

Fig. 11

The interpolant of two parallel planes smoothly moves between the start and end points (green to red) while maintaining the direction of the normal

Fig. 12

The interpolant of two anti-parallel planes (green to red) must go via infinity due to the sign change. Care must be taken with the orientation of objects when designing algorithms using these interpolations

11 Spheres

The interpolant of spheres has been studied before in [2] and [4]. As with planes, all interpolants of spheres are valid objects as $\langle \Sigma _1\Sigma _2\rangle _4 = 0$ and have the property of making contact with the meet of the spheres at all points during the interpolation. We can see the form of the interpolant sphere by considering its dual form:

$$\begin{aligned} I_5\Sigma _3 = \alpha I_5\Sigma _1 + (1-\alpha )I_5\Sigma _2 \end{aligned}$$

The dual form of a sphere can be decomposed into the sum of the conformal centre point P and negative half the radius squared times $n_{\infty }$:

$$\begin{aligned} I_5\Sigma = P - \frac{1}{2}\rho ^2n_{\infty }\end{aligned}$$

the interpolation of the dual of two spheres is therefore

$$\begin{aligned} I_5\Sigma _3 = \alpha P_1 + (1-\alpha )P_2 - \frac{1}{2}(\alpha \rho _1^2 + (1-\alpha )\rho _2^2)n_{\infty }\end{aligned}$$

For two concentric spheres ie. $P_2 = P_1$ we can therefore see that the interpolation between them will remain centred in the same place and will simply have a radius $\rho _3$ which varies as $\rho _3^2 = \alpha \rho _1^2 + (1-\alpha )\rho _2^2$.

As we have seen previously, the interpolation of two conformal points $P_1$ and $P_2$ is of the form

$$\begin{aligned} \alpha P_1 + (1-\alpha )P_2 = F(\alpha p_1 + (1-\alpha )p_2) - \alpha (1-\alpha )(P_1\cdot P_2)n_{\infty }\end{aligned}$$

we can therefore also write the interpolation of two non-concentric spheres as:

$$\begin{aligned} I_5\Sigma _3 = F(\alpha p_1 + (1-\alpha )p_2) - \alpha (1-\alpha )(P_1\cdot P_2)n_{\infty }- \frac{1}{2}(\alpha \rho _1^2 + (1-\alpha )\rho _2^2 )n_{\infty }\end{aligned}$$

Collecting like factors shows that the centre point of the interpolated sphere moves linearly along the line joining $p_1$ and $p_2$

$$\begin{aligned} I_5\Sigma _3 = F(\alpha p_1 + (1-\alpha )p_2) -\left( \alpha (1-\alpha )(P_1\cdot P_2) + \frac{1}{2}(\alpha \rho _1^2 + (1-\alpha )\rho _2^2) \right) n_{\infty }\end{aligned}$$

Furthermore, writing the dot product of points in terms of their euclidean vectors we can see that the radius of the sphere varies along its interpolation path

$$\begin{aligned} I_5\Sigma _3 = F(\alpha p_1 + (1-\alpha )p_2) -\frac{1}{2}\left( -\alpha (1-\alpha )(p_1-p_2)^2 + \alpha \rho _1^2 + (1-\alpha )\rho _2^2 \right) n_{\infty }\end{aligned}$$

and so the radius $\rho _3$ varies as

$$\begin{aligned} \rho _3^2 = -\alpha (1-\alpha )(p_1-p_2)^2 + \alpha \rho _1^2 + (1-\alpha )\rho _2^2 \end{aligned}$$

For fixed values of $\rho _1$ and $\rho _2$ this implies $\rho _3^2$ varies as $-(p_1 - p_2)^2$ and so the further apart the two spheres are the smaller the radius of the interpolant. To find turning points we differentiate with respect to $\alpha$

$$\begin{aligned} \frac{d\rho _3^2}{d\alpha } = (-1+2\alpha )(p_1-p_2)^2 + \rho _1^2 -\rho _2^2 \end{aligned}$$

setting this to zero yields a single turning point at

$$\begin{aligned} \alpha = \frac{\rho _2^2 -\rho _1^2 + (p_1-p_2)^2}{2(p_1-p_2)^2} \end{aligned}$$

Considering the second derivative

$$\begin{aligned} \frac{d^2\rho _3^2}{d\alpha ^2} = 2(p_1-p_2)^2 \end{aligned}$$

we see that this is always positive and so the stationary point is a minimum.

For the case that the surfaces of $\Sigma _1$ and $\Sigma _2$ are just touching we have the condition

$$\begin{aligned} (p_1 - p_2)^2 = (\rho _1 + \rho _2)^2 = \rho _1^2 + \rho _2^2 + 2\rho _1\rho _2 \end{aligned}$$

returning to the first derivative in this case

$$\begin{aligned} \alpha = \frac{2\rho _2(\rho _1 + \rho _2)}{2(\rho _1 + \rho _2)^2} = \frac{\rho _2}{(\rho _1 + \rho _2)} \end{aligned}$$

this value of $\alpha$ is the point at which the centre of the interpolant sphere lies on the surface of both spheres. At this point the squared radius is zero:

$$\begin{aligned} \rho _3^2= & {} -\frac{\rho _2}{(\rho _1 + \rho _2)}\frac{\rho _1}{(\rho _1 + \rho _2)}(\rho _1 + \rho _2)^2 + \frac{\rho _2}{(\rho _1 + \rho _2)}\rho _1^2 + \frac{\rho _1}{(\rho _1 + \rho _2)}\rho _2^2 \\ \rho _3^2= & {} \frac{-\rho _2\rho _1(\rho _1 + \rho _2) + \rho _2\rho _1^2 + \rho _1\rho _2^2}{(\rho _1 + \rho _2)} = 0 \end{aligned}$$

Pulling the spheres further apart from this point so that they no longer intersect will therefore produce a sphere with negative radius, an imaginary sphere. These results are already known [2] and are here included for completeness.

12 Applications

The ability to interpolate geometric objects suggests a wide variety of applications in the areas of computer vision and graphics. There are many traditional algorithms in vision that rely solely on point information from images and ignore lines and other, potentially useful, geometric primitives. Many of these algorithms have been non trivial to translate into the framework of CGA due to having to specify transformations between objects explicitly rather than implicitly via the objects themselves. The ability to average geometric objects directly suggests immediate applications in clustering of objects extracted from real data, interpolation to produce surfaces and other areas for problems we might normally use linear algebra.

12.1 Higher Order Spline Interpolation Through Objects

With the ability to construct arbitrary linear combinations of blades we naturally might wonder about the applications of this to spline generation through control objects. Figure 13 shows an example of interpolating through different control objects with different orders of spline. As expected, higher order interpolation produces smoother surfaces through our objects.

Fig. 13

Interpolation through control objects. Top: circles. Bottom: point pairs. Interpolation type: a, d linear, b, e quadratic, c, f cubic

12.2 Recursive Scene Simplification by Averaging Conformal Objects

Fig. 14

A 3D line model before (a) and after (b) recursive scene simplification

When extracting geometric primitives from triangulated CAD models from point cloud data or from images, there are often many objects that lie close to each other in space. Line segment detectors, for example, will often extract long lines as multiple line segments that need stitching together. We would like a way of simplifying these noisy models by collapsing objects that are close together into a single object. One way to do this is via a recursive filtering algorithm as follows:

• 1. Set a minimum cost threshold for difference between objects

• 2. Compute the cost between all objects of the same grade in the scene

• 3. If all costs are above the threshold then terminate the algorithm

• 4. Average the two objects with the smallest cost

• 5. Return to step (2)

This leads to a simplified model that retains the core features of the original model. For comparison of objects $X_i$ and $X_j$ we use the cost function $C_{ij}$ for a rotor $R_{ij}$ as defined in [7]:

$$\begin{aligned} C_{ij} = \langle (R_{ij} - 1)({\tilde{R}}_{ij} - 1){\rangle }_0 + \langle R_{ij\parallel } {\tilde{R}}_{ij\parallel }{\rangle }_0 \end{aligned}$$

(13)

where $R_{\parallel }=R\cdot e$, and gives the component of R having $n_{\infty }$ as a factor and $R_{ij}$ is the rotor that takes $X_i$ to $X_j$ as described in [11]. An example of this algorithm working on simulated lines is shown in Fig. 14.

This algorithm is simply one way to perform scene simplification and it has a high computational complexity making it run slowly for large numbers of objects, but is included here as an example of one potential area the averaging of object methodology may be applied to.

12.3 k-Means Clustering of Conformal Objects

One of the most fundamental and simple clustering algorithms is known as k-means clustering [14]. Consider a 3d scene composed of k geometric objects of a given grade. We have multiple noisy observations for each object and so would like to fit k centroids to these clusters to represent the “true” objects in the world.

Fig. 15

Three clusters of 3D lines correctly segmented by the algorithm

Fig. 16

Three clusters of 3d circles correctly segmented by the algorithm. The black circles here are the final computed cluster centroids

The steps for implementing this clustering are given below:

• 1. Randomly assign k objects to be the initial positions of the cluster centroids, leave all other objects unassigned

• 2. Assign each object in the scene to the centroid closest under our given cost metric, again we use the cost function given in Eq. (13)

• 3. If this is not our first iteration and no objects have changed assignment then terminate the algorithm

• 4. The centroid of each cluster is moved to the mean of the objects assigned to it, where mean is defined as the sum of the objects in the cluster projected back onto the blade manifold

• 5. Go to step (2)

Figures 15 and 16 show the successful application of this algorithm on simulated data—each line or circle has been associated with the cluster (indicated by colour) to which it is most likely to belong. One of the key advantages of using the averaging of objects and correction back to a blade for this algorithm is that it is computationally cheap. A typical approach in GA to this kind of problem might involve attempting to find the mean of a given cluster by optimisation of our cost function through a space parameterising our centroid objects. Here we can simply average the objects in each cluster making it feasible to cluster very large numbers of conformal objects quickly.

12.4 Closest Point to Two Non-intersecting Lines (Least Squares Sense)

Consider two non-intersecting non-coplanar lines in 3d space, $L_1$ and $L_2$. We wish to find the point P that lies closest to both in a least squares sense. First we will construct two orthogonal intermediary lines $L_+ = S_+(L_1 + L_2)$ and $L_- = S_-(L_1 - L_2)$ where S(X) represents the projection of a 3-vector X back onto the line manifold. $L_+$ and $L_-$ both lie half way between the two original skew lines but intersect at right angles . The intersection of these lines is the point P that lies half way between the original lines. To extract this point of intersection we can follow the formula given in [12]:

$$\begin{aligned}&Q = (L_-n_0L_-)n_{\infty }(L_-n_0L_-) + L_+(L_-n_0L_-)n_{\infty }(L_-n_0L_-)L_+ \\&P = \frac{-Q n_{\infty }Q}{(Q n_{\infty }Q)\cdot n_{\infty }} \end{aligned}$$

13 Conclusions

This paper has shown how we are able to add multiples of conformal objects by factoring the resulting multivector into a scalar plus 4-vector term and a valid geometric object. We have then investigated the form of this multivector for each grade of conformal object. Using the ideas of interpolating and averaging objects, a range of applications are suggested with relevance in computer vision and computer graphics.