Analysis of a Three-Bar Kolsky Apparatus for High-Rate Three-Point Flexure

Abstract

A Kolsky bar method is described that is suitable for measuring the flexural strength of ceramics under valid testing conditions in a high-rate three-point bending configuration. A three-bar arrangement is used—one input bar and two output bars—to provide measurements of force and displacement at each loading point. Small diameter bars are used to improve the force measurement made by the incident bar which in many cases would be inaccurate. An analytical model is formulated to predict the desired incident pulse based on the conditions of the experiment and the desire for a particular prescribed strain-rate. A finite element analysis is also conducted to determine suitable specimen geometries that will yield valid data at the desired rate. It is shown that stiff beam geometries improve specimen equilibrium and can reduce inertial effects. However, the use of small diameter bars necessitates unusually precise pulse-shaping. To achieve additional flexibility in pulse-shaping, a tapered striker is used in conjunction with a ductile wave-shaper to generate the desired incident pulse. A down-side of this approach is that a suitable taper geometry must be determined. It is shown that this geometry can be designed quickly and accurately using a simple one-dimensional finite element approach. The methods are demonstrated by measuring the dynamic flexural strength of α-SiC.

Introduction

Ceramics such as SiC, B₄C and Al₂O₃ that combine high-hardness with low-density are considered promising materials to provide protection during impact events [1]. Over the past several decades modeling and simulation tools have been developed to predict material response during such events. These models commonly incorporate ceramic property values such as hardness, toughness and strength as input parameters. Unfortunately most of the data on these ceramics has been generated in the quasi-static load regime and may not be appropriate for predicting material performance at high loading rates. Since many ceramics display rate-dependent properties, the measurement of dynamic properties is critical to accurate modeling. Dynamic properties of ceramics are often measured by some variation of the the Kolsky bar, or Split Hopkinson Pressure Bar (SHPB). Most dynamic testing methods based on the Kolsky bar are adaptations of quasi-static techniques. Measuring the tensile strength of a ceramic material has always been complex as variance in processing, flaw type/distribution, specimen size, and loading configuration typically result in different strength values for the same ceramic composition. Direct tension tests are preferred but these tests are difficult and expensive, even at quasi-static loading rates. Thus, the majority of ceramic tensile data is obtained by indirect means such as flexural testing. There are several standardized methods of obtaining [2–4] and analyzing [5–7] ceramic tensile strength data from flexure testing.

Most of the effort directed towards placing ceramic specimens into flexure has been in pursuit of measuring the dynamic fracture toughness using pre-cracked beams, although many of the basic principals apply to the determination of flexure strength as well. Jiang and Vecchio [8] reviewed numerous techniques used in the measurement of dynamic fracture toughness including one, three, and four-point bending techniques. Again, these are in large part adapted from low-rate methods, and can be differentiated by the number of input/output bars used to measure the signal. Most Kolsky bar techniques place a specimen between a single input (incident) and a single output (transmission) bar which generally requires a large diameter bar (or tube) so that the desired loading span can be incorporated within the bar cross-section. However, this large bar diameter can lead to a very weak transmitted pulse and an inadequate measurement of the load at fracture. This can necessitate the use of quartz gauges on either side of the specimen to measure load and verify dynamic equilibrium. This is demonstrated in both four-point [9], and three-point bending [10], using two-bar arrangements. An alternative is to test a specimen with a loading span larger than the bar diameter by using an output bar placed at both support points. This naturally leads to three-bar/three-point bend arrangements, where the load supported by each output bar is half that applied by the input bar. This is demonstrated on large specimens, by Yokoyama and Kishida [11], Ogawa et al. [12] and Delvare et al. [13].

Single point bending is an additional approach, and has an advantage in that it avoids many alignment problems. Belenky and Rittel [14–16] have recently used a one-point bending technique to measure dynamic flexural strength of ceramics. In this technique, an incident bar is used to directly impact a free standing specimen. The technique relies upon the inertia of the specimen to cause fracture before loss of contact between the specimen and the bar occurs. This technique is not based upon an assumption of quasi-static behavior within the specimen, and because of this it is a promising approach to measure flexural strength at very high rates.

The same arrangement used in prior three-bar three-point bend work can be applied to smaller specimens by using proportionally smaller input/output bar diameters. Miniaturized Kolsky bars have many advantages, and have been used to load metals in compression at high strain rates for some time [17]. The smaller bar diameter reduces the rise-time of the signals and increases the fidelity at which high-frequencies propagate within the bars. Small bar diameters also lower the impedance of the bar and can improve the measurement of forces applied to the specimen as well. An assessment of the advantages of a miniaturized Kolsky bar compression test has been reported by Jia et al. [18].

The present study builds upon previous three-bar, three-point bend work on both fracture toughness [11] and flexural strength [12, 13]. Central to our work is the concept of reducing bar diameter to validate equilibrium by direct force measurement and adapting specimen dimensions to improve specimen equilibrium conditions at a desired loading rate. It is shown that the input/output bar diameters can be optimized to obtain high quality flexural strength data—including the high-quality measurement of force at all loading points, using a standard strain-gage approach. This avoids the use of quartz gages which can be sensitive to calibration and inertial errors. It also greatly improves the temporal measurement of force, which is a significant advantage when testing brittle materials where rapid fracture is expected. Alternate beam geometries (increased stiffness/short span) are investigated numerically with the intent of improving equilibrium conditions during high-rate loading. It is also shown that the incident pulse needed to load a specific sample at a specific rate can be calculated precisely, and a new approach to pulse shaping is proposed. This method involves the use of variable impedance strikers along with traditional deformable wave-shapers at the tip of the input bar, and greatly increases the range of incident pulse shapes that can be obtained experimentally. This makes the pulse-shaping process predictive, not trial and error, and improves the overall testing procedure. Flexural strength data for α-SiC over a range of strain-rates is presented as an application.

Experimental Approach

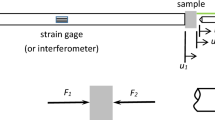
A three-bar, three-point-bend Kolsky bar is shown in Fig. 1. The input bar is impacted by a striker, not shown, and initially loads the specimen. The two output bars provide the reaction forces. The input bar is made from 3.18 mm diameter 7075-T6 aluminum (ρ _i  = 2,777 kg/m³, c _i  = 5,030 m/s), and is 1,788 mm long. While all of the experiments discussed herein use this input bar, data from experiments using two sets of output bars will be presented. Both sets are made from 7075-T6 aluminum (ρ _o  = 2,777 kg/m³, c _o  = 5,030 m/s). Their lengths range from 940 to 1,020 mm, long enough so that no reflections occur during the testing window. More significantly, they differ in diameter, the first at 3.18 mm and the second at 6.35 mm. All bars are supported with fixed bushings (brass or Teflon) to maintain a symmetric three-point loading with a 20 mm span (L = 20 mm). The input bar is instrumented with a set of Vishay Micro-Measurements EA-13-062AQ-350 strain gages at the midpoint (L _SG1 = 894 mm). The output bars are instrumented with Kyowa semi-conductor strain gages (KSP-2-1 K-E4), 10 bar-diameters from the loading ends (L _SG2 = 32 mm or 64 mm, for the smaller and larger bars, respectively). The end of each 3.18 mm diameter bar (input and output) is machined into a roller shape with a 3.18 mm diameter, as shown in Fig. 2a. This generates a line-load on the specimen, with at most a 3.18 mm length. The 6.35 mm output bars have half-cylindrical rollers epoxy-bonded to the loading ends, as shown in Fig. 2b. The rollers are 7075-T6 aluminum, 3.18 mm in diameter, and 4 mm long. These roller designs minimize the amount of additional fixtures needed to load the specimen; the impedance of each bar varies only over the small length of the roller geometry (1.59 mm). Based on machining tolerances, it is estimated that the contact roller surfaces are parallel to one another, and the specimen, to within 30 μm.

Fig. 1

A 3-point bend Kolsky bar

Fig. 2

Roller designs for 3.18 and 6.35 mm output bars

In most cases with ceramic specimens, the sample is linear-elastic until fracture. If the specimen is in a state of quasistatic equilibrium and is sufficiently long and slender, standard elementary beam theory applies. The applied load, P, and resulting beam deflection, δ, are related by

$$ \delta = \frac{{PL^{3} }}{48EI} $$

(1)

where E is the elastic modulus of the beam and I the moment of inertia (=bh ³/12). Maximum tensile stress, σ, and corresponding strain, ε, occur at the midpoint (point A in Fig. 1) and are given by

$$ \sigma = \frac{3PL}{{2bh^{2} }} = E\varepsilon . $$

(2)

This can be used to determine the flexure strength once the load at failure has been measured.

The assumption of quasi-static equilibrium, assuming symmetric loading, implies

$$ P = F_{1} = 2F_{2a} = 2F_{2b} . $$

(3)

This immediately comes into question during high-rate experiments. In the three-bar arrangement, each bar is in theory capable of measuring the loads applied to the sample, and therefore a validation of specimen equilibrium is available. This is done using standard equations.

$$ F_{1} = \left( {\varepsilon_{i} + \varepsilon_{r} } \right)E_{i} A_{i} $$

(4)

$$ F_{2a} = \varepsilon_{t,a} E_{o} A_{o} $$

(5)

$$ F_{2b} = \varepsilon_{t,b} E_{o} A_{o} $$

(6)

Here ε _i , ε _r , ε _t,a , and ε _t,b are the incident, reflected, and transmitted pulses in both output bars (a and b), translated temporally to the time at which they act at the sample, accounting for dispersion [19–21]. E _i , and E _o , are the elastic moduli of the input and output bars, and A _i and A _o are the cross-sectional areas.

These equations can be used to explain the selection of the bar geometries/materials chosen. For the types of materials and beam geometries that this facility was designed for, failure loads in the range of 200–1,500 N are expected. The primary measurements of interest are the forces given by Eqs. (4–6). Forces F _2,a , and F _2,b are determined in a straightforward manner using strain-gage measurements of the transmitted pulses. With 3.18 mm diameter aluminum output bars, strains of 270–1,100 μ result; with 6.35 mm diameter bars, strains of 70–300 μ result. These strain levels are well within the measurement capabilities of the semi-conductor strain gages used, and accurate results can be expected.

The measurement of F ₁ is more problematic because it involves the summation of the incident and reflected pulses, Eq. (4). If the sample is weak in comparison to the impedance of the input bar, the incident and reflected signals will be close in magnitude but opposite in sign. The sum will be small in comparison to the error that is present in the strain gage measurements, and the force measurement will be poor. Decreasing the impedance of the bar, for example by reducing its diameter, decreases the magnitude of the reflected signal, and measurement accuracy increases. If the diameter is decreased sufficiently, the reflected pulse will become compressive, and lead to accuracies comparable to those made by the transmitted bars. Thus the bar impedance should be “matched” to the specimen, and this is the rationale behind using the small diameter input bar for these experiments.

The velocities v ₁, v _2,a , and v _2,b , can also be determined from the measured strain pulses.

$$ v_{1} = \left( {\varepsilon_{i} - \varepsilon_{r} } \right)c_{i} $$

(7)

$$ v_{2,a} = \varepsilon_{t,a} c_{o} $$

(8)

$$ v_{2,b} = \varepsilon_{t,b} c_{o} $$

(9)

Displacements u ₁, u _2,a , and u _2,b are determined by time integration. Because the analysis of waves within the pressure bars assumes constant impedance (i.e., cross-sectional area), the force and velocity measurements are made at the interfaces where the bars transition to the roller geometry. This is emphasized in Fig. 1. This may seem to be a minor point, but in the experiments and simulations that follow the roller sections of the bars contain a non-negligible compliance that should be considered. If the rollers remain elastic, their deformation is related to the applied force by a spring constant k _R , i.e., δ _R  = P/k _R . Beam deflection is therefore related to the measured deflections by

$$ \delta = u_{1} - u_{2} - \delta_{R} = u_{1} - u_{2} - P/k_{R} $$

(10)

where we have assumed symmetry of the two output bars, u _2,a  = u _2,b  = u ₂. If Eq. (1) is valid, P can be eliminated.

$$ \delta = \frac{{u_{1} - u_{2} }}{{1 + {\raise0.7ex\hbox{${48EI}$} \!\mathord{\left/ {\vphantom {{48EI} {k_{R} L^{3} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${k_{R} L^{3} }$}}}} $$

(11)

The goal of the high-rate experiments is to determine flexure strength at an elevated strain-rate, $\dot{\varepsilon }$, for the material in question. Assuming failure initiates at point A in Fig. 1, the location of maximum tensile stress, Eqs. (1) and (2) apply and the strain-rate at the failure location can be related to the deflection in Eq. (11) by

$$ \dot{\delta } = \frac{{\dot{\varepsilon }L^{2} }}{6h} . $$

(12)

Specimen Geometry and Loading Rate

Because these experiments use Eq. (2) to determined flexural strength from the measured loads at failure, an adequate state of quasi-static equilibrium is required. Kolsky bar samples reach equilibrium through the propagation of stress-waves. If many wave-transits occur during the test duration, a specimen is likely to reach equilibrium. For bend specimens, some insight can therefore be gained from basic observations of flexural waves in linear elastic materials. The group velocity for flexural waves (long wave-lengths) in a beam with rectangular cross-section is

$$ {\text{c}}_{\text{g}} = \frac{{2\pi {\text{h}}}}{\varLambda }\sqrt {\frac{\text{E}}{ 3\rho }} $$

(13)

where Λ is the wave-length of the signal [22, 23]. Note the wave-speed, which is strongly dependent on wave-length, is not only a function of material properties (E and ρ) but also the “height” dimension, h, since an increase in h increases the stiffness of the beam. Thus beam geometries with a high moment of inertia will equilibrate more rapidly than those with a lower moment of inertia because of the increased wave speed. Furthermore, a specimen with a smaller span equilibrates more quickly than one with a longer span simply because the relevant stress-waves have less distance to travel to the remainder of the specimen. Another way to consider this is to observe that the natural frequency of a beam increases as moment of inertia increases and length decreases. The fundamental frequency for a beam in three-point bending is given by

$$ f_{1} = \frac{2.833h}{{L^{2} }}\sqrt {\frac{E}{\rho }} . $$

(14)

Increasing the height dimension or reducing length both increase the natural frequency, and reduce the odds of exciting fundamental frequencies during loading. Sample geometry is therefore an important consideration from an equilibrium standpoint, and a logical approach is to make the sample as small and as stiff as other factors allow, specifically that the elementary theory (Eq. 1) remains sufficiently accurate. Finite element analysis is an ideal way to study these effects, and is the approach taken here.

Three beam orientations are now considered, as tabulated in Table 1. The fundamental frequencies for each, from Eq. (14), along with the corresponding periods, T, are also given. Finite element analyses were performed of each under various loading conditions using the Elastic Plastic Impact Calculations code (EPIC) [24]. All of the simulations were two-dimensional plane-stress, used half-model meshes with a symmetry boundary condition, and include the specimen and rollers. The pressure bars were not included since the wave-propagation in the bars is well-understood. This omission simplifies the calculations and greatly reduces computation times. As an example, the mesh for configuration B is shown in Fig. 3. All elements are three-node triangles in the “cross-triangle” arrangement, i.e., they are generated from a quadrilateral mesh by splitting each quadrilateral into four triangles by adding a mid-point node. Triangular elements were used to eliminate the possibility of hour-glassing that sometimes occurs with quadrilaterals, and the cross-triangle pattern was used to avoid element “locking.” The rollers are meshed with 8 elements along the radius, and the beam is meshed with a cross-triangle “quadrilateral” 100 μm in size. The element dimensions for the remaining meshes (configurations A and C) are similar. The rollers are modeled as linear elastic aluminum (ρ = 2,777 kg/m³, G = 27.6 GPa, K = 76.7 GPa) and the beam as linear elastic SiC (ρ = 3,120 kg/m³, G = 187 GPa, K = 213 GPa). A failure stress of 400 MPa is assumed for the SiC, using a simple maximum tensile stress criterion.

Table 1 Three beam geometries considered for high-rate three-point flexure

Fig. 3

Mesh used for simulations of configuration B. The shaded element is at the element from which data are taken

In terms of beam loading rate, we ultimately want to control the strain-rate at the fracture location, $\dot{\varepsilon }\left( t \right)$. In other words, we want to apply boundary conditions such that we obtain a pre-determined $\dot{\varepsilon }\left( t \right)$. This dictates the deflection rate, $\dot{\delta }$, according to Eq. (12). We can achieve this rate simply by fixing the bottom roller and applying the deflection to the top roller in Eq. (11), v ₂ = 0 and $v_{1} = \dot{\delta }\left( {1 + 48EI/k_{R} L^{2} } \right)$. However, the goal is to mimic loading in a Kolsky bar, and this approach misses important inertial effects because it ignores the motion of the output bar. Instead, it is necessary to determine nodal velocities by combining Eqs. (1, 3, 5, 6, 8–10, and 12).

$$ v_{1} = v_{2} + \frac{{\dot{\varepsilon }L^{2} }}{6h}\left( {1 + \frac{48EI}{{k_{R} L^{3} }}} \right) $$

(15)

$$ v_{2} = \frac{{4EIc_{o} \varepsilon }}{{E_{o} A_{o} h}} $$

(16)

In these equations, specimen equilibrium has been assumed. However, the simulations are intended only as guidance for the experiments, and we do not intend to perform experiments where non-equilibrium effects are large. Roller stiffness, k _R , can be determined from the simulations by relating roller deflection to applied load. This was done and found to be 75 MN/m, essentially treating both rollers as a single spring in series with the sample. This value can then be used in Eqs. (15–16) to determine nodal velocity.

Any number of strain-rate profiles could be applied in these simulations. To simplify, constant strain-rates of 5 and 20/s, with a sinusoidal ramp for the initial 35 μs according to $\dot{\varepsilon }\left( t \right) = \dot{\varepsilon }_{o} \frac{1}{2}\left( {1 - { \sin }(89,760s^{ - 1} t + \pi /2)} \right)$ was applied. This is shown in Fig. 4. Also shown are the nodal velocities required to achieve this strain-rate for an α-SiC specimen, geometry B, under three different loading cases: (1) an applied rate of 5/s and 3.18 mm diameter output bars (2) a rate of 20/s and 3.18 mm output bars, and (3) 20/s and 6.35 mm diameter output bars.

Fig. 4

Example target strain-rates used in the simulations, 5/s and 20/s. The nodal velocity profiles, v ₁ and v ₂, are also given (solid and dashed lines) for three cases with beam geometry B. Note failure at a strain-rate of 5/s occurs after ~250 μs and at ~65 μs at 20/s

Results from 6 simulations are presented next to investigate the validity of using Eq. (2) for determining flexural strength from measured force for various beam geometries and loading conditions. These simulations are summarized in Table 2, and results are presented in Fig. 5. Forces F ₁ and F ₂ are measured from the simulations by summing nodal forces along the top and bottom surfaces of the rollers (where the nodal velocities are prescribed). This mimics the force measurements that would be made in an experiment. The stress at the fracture location, unknown in the experiment, can be determined directly in the simulation from the element at that approximate location (shaded in Fig. 3).

Table 2 Summary of simulations

Fig. 5

Results from the simulations described in Table 2

From Eq. (2), P varies linearly with σ, and can be plotted for various beam geometries. This has been done for each simulation in Fig. 5b, d, f, h, j, and l, and represents “ideal” behaviors (dashed lines). Deviations from the ideal, due to for example non-equilibrium or the slender beam assumption, can be assessed by comparing the ideal to the actual relationships between nodal forces and element stress determined from the simulations. It is also useful to plot the forces F ₁ and F ₂ as functions of time, Fig. 5a, c, e, g, i, k, since equilibrium implies they must be the same (Eq. 3).

The first simulation is of geometry A loaded to produce a strain-rate of 5/s with an assumed output bar diameter (d_o) of 3.18 mm. This specimen has a total length of 50 mm, a span of 40 mm, and a 3 mm × 4 mm cross-section oriented such that the shorter dimension is along the loading direction. This orientation gives a moment of inertia of 9 mm⁴ (the “low” moment-of-inertia orientation). Figure 5a shows the forces F ₁ and F ₂ determined from the simulations as functions of time. There are several features worth noting. The first is the delay associated with F ₂. Whereas F ₁ rises instantaneously upon loading, F ₂ lags by approximately 0.02 ms, the time needed for the mechanical signal to travel the distance from the input bar roller to the output bar. The second is the oscillations that occur in each signal. These are due to non-equilibrium effects in the beam, and, not surprisingly, their frequency (~70 kHz) approximately matches the natural frequency of the beam given in Table 1 (63 kHz). The oscillations are larger in magnitude in the output bar measurement, although the reason for this is not clear. Figure 5b plots element stress with each force, F ₁ and F ₂, along with the ideal behavior. Again, the oscillations are evident, although the general trend is that each stress calculation roughly follows the ideal solution.

Based on the arguments above, one way equilibrium can be improved is by reducing beam/span length, e.g., to geometry B in Table 1.¹ This can be done without changing the target strain-rate, although it requires a different set of nodal velocities as determined by Eqs. (14) and (15). To see the effect of changing the length only, however, it is important to keep the strain-rate the same. The results of this second simulation, with a 25 mm length and a 20 mm span, are shown in Fig. 5c, d. In comparison to the prior results with the longer length, the oscillations, the F ₂ measurement delay, and the deviation from the ideal solution, are all greatly decreased. Again, this was achieved simply by decreasing the specimen length and the length of the support span.

Obviously, these results cannot be extrapolated to all loading conditions. If the strain-rate is increased to 20/s, using the same short specimen, inertial effects return to noticeable levels. This is shown by the results from simulation 3 in Fig. 5e, f, where similar general observations were seen in Fig. 5a, b, i.e., oscillations, etc. However, it is now possible to discern basic inertial effects from the data. It is observed that F ₁ over-estimates the force that would be measured in the ideal case, and a flexural strength made with this measurement would be artificially high. Conversely, F ₂ under-estimates the force measurement and a flexural stress based on this measurement would be artificially low. In this case, the error can be attributed in large part to the higher acceleration required to obtain the higher rate. This can be seen by referring back to Fig. 4, which shows the applied velocity for simulations 2 and 3 (grey and red curves for 5 and 20/s, respectively). Each requires a linearly varying velocity over much of the loading duration, and constant accelerations of ~12 and 46 km/s². In the most basic analysis, this leads to an inertial force equal to the product of the mass of the beam (0.93 g) and the acceleration. At 5/s, this force is only 9 N, about 2 % of the peak measured force. However, at 20/s, it is 35 N or about 8 % of the peak measured force. Thus in the latter case the inertial error is much more significant (the 35 N inertial error is depicted graphically in Fig. 5f for comparison). As expected, averaging the forces leads to a much better approximation of the ideal case. This is also shown in Fig. 5f.

The inertial errors seen in Fig. 5e, f are largely a result of the rigid body acceleration of the beam, rather than an effect of wave propagation in the specimen. They can therefore be decreased by limiting this acceleration. This can be done without changing the beam geometry or compromising the target strain-rate of 20/s by increasing the output bar stiffness, for example by increasing diameter to 6.35 mm. The results for this situation (simulation 4) are shown in Fig. 5g, h. Because of the stiffer output bars the input velocities (also shown in Fig. 4) yield a decreased acceleration by a factor of ~4. The inertia is decreased by a corresponding amount. This is seen in Fig. 5g, h, where the errors are reduced to negligible levels (approximately 2 % of the peak force).

As discussed above, increasing the moment of inertia increases the natural frequency and can also improve the state of equilibrium within the beam. However, inertial errors of the type discussed here still remain. To see this, Fig. 5i, j show results for a beam geometry C, which is a short-span beam loaded with the high moment-of-inertia orientation (16 mm⁴). This simulation (simulation 5) assumes 3.18 mm output bars and a target strain-rate of 20/s. Inertial errors return. As before, a possible solution, other than reducing the strain-rate, is to increase output bar diameter, for example again to 6.35 mm. This result (simulation 6) is shown in Fig. 5k, l, where the inertial effects have again been mitigated.

Pulse Shaping

While loading rate can be easily controlled in the simulations by setting nodal velocity, it presents significant challenges in the experiments. Again, the goal is to load the beam in such a way as to produce the desired strain-rate, $\dot{\varepsilon }\left( t \right)$. With Kolsky bar experiments, this is done through pulse-shaping, methods which tailor the incident pulse to produce the desired loading. Once $\dot{\varepsilon }\left( t \right)$ has been decided upon, Eqs. 1, 3–10, and 12 can be combined to solve for the incident pulse, ε _i , required to produce this strain-rate within the sample.

$$ \varepsilon_{i} = \frac{{L^{2} }}{{12hc_{i} }}\left[ {\dot{\varepsilon }\left( {1 + \frac{48EI}{{k_{R} L^{3} }}} \right) + \varepsilon \frac{48EI}{{L^{3} }}\left( {\frac{{c_{i} }}{{E_{i} A_{i} }} + \frac{{c_{o} }}{{2E_{o} A_{o} }}} \right)} \right] $$

(17)

The next step is to determine a method to generate this pulse. The most common method for creating various pulse shapes is through the use of deformable wave-shapers placed between the striker and the input bar, e.g., [25–27]. The challenge here is to find a shaper (material and geometry) that gives the incident pulse required. Another method, less commonly used, is to vary the impedance of the striker to create the desired incident pulse, e.g., by using a tapered striker rather than one with a constant cross-sectional area. The design of such strikers can be done iteratively in an inverse approach [28], or solved for directly [29, 30].

Unfortunately, wave-shapers could not be found to generate the desired incident pulses for these experiments. Suitable tapered strikers were next designed using the method of [30]. However, these designs led to “sharp-pointed” strikers, which could not be used in practice because they would not remain elastic when impacted against the input bar at the necessary speeds. In the end, an acceptable solution was found by combining both methods—deformable wave-shapers that were impacted with a tapered striker. The shape of this striker was determined using an iterative approach using one-dimensional explicit finite element calculations. These simple models included the striker, wave-shaper, and input bar. Striker shape, material, and impact speed were varied systematically for a variety of known wave-shaper responses until a shape was determined which yielded a close approximation of the incident pulses needed for the experiments presented below. This procedure is detained in the Appendix. A target rate of 10/s, after an approximate 35 µs rise, was used. In general, a different striker/shaper design is needed for each choice of strain-rate, beam geometry, and output bar. However, the final design was chosen to be a compromise to approximate this rate with two different output bars (3.18 and 6.35 mm) simply by varying impact speed.

The final striker was made from polycarbonate (ρ = 1,200 kg/m³ and c = 1,460 m/s), 100 mm long, with a diameter, d, that varied from 3.4 mm (impact end, x = 100 mm) to 9.5 mm (free-end, x = 0 mm) according to d = (0.0000148 mm⁻²)x ³ − (0.00208 mm⁻¹)x ² + 0.00530x + 9.5 mm. Striker impact speeds ranged from 10 to 14 m/s. Wave-shapers were cut from 1.0 mm diameter drawn aluminum wire (99.999 % pure), lengths ranging from 0.9 to 1.1 mm. These were compressed diametrically, and were adhered to the input bar with a small amount of vacuum grease. The impacting end of the striker has a thin aluminum cap (3.2 mm diam, 3 mm thick) in order to avoid damaging the striker on impact, a minor modification that does not noticeably affect the incident pulse shape. A thin sabot, ~2 mm thick, 25 mm from the impact end, was used to properly orient the striker in the barrel (9.51 mm bore). Note that polycarbonate was used to simplify machining. Although perhaps a more obvious choice, an aluminum striker to accomplish the same loading would have had to be much thinner and longer, and would have had no significant advantage over polycarbonate.

Experimental Results

Low-Rate Experiments

A hot-pressed α-SiC was selected to illustrate the experimental technique. It was under evaluation for possible use as an impact resistant material. It was obtained in plate form, from which beam specimens nominally 3 × 4 × 50 mm were machined according to the procedures outlined in ASTM C1161. The average four-point flexure strength of this α-SiC was determined to be 292 ± 46 MPa in a separate study.

Additionally, low-rate flexure strengths were determined as part of this effort using the beam orientations and span lengths listed in Table 1, all in three-point bend. The strength of ceramics is not only dependent upon the rate of loading, but also the specimen size. This is termed strength size scaling, and is a function of the amount of material in a specimen placed in the maximum stress state [7]. It is therefore important to confirm that the flexure strengths measured from each geometry are consistent before adding the additional complication of whether the flexure strength is rate-dependent.² A strain rate of approximately 10⁻⁶/s was used in all tests. These low-rate experiments were performed on an Instron model 1123 screw-driven load frame. The shorter length specimens were created by cutting the beam specimens in half with a diamond saw. These short specimens were then tested in either the low moment of inertia (nominally 9 mm⁴) orientation or a high orientation (~16 mm⁴). While these are not standard configurations for quasi-static flexure strength testing, these values can be compared to the four-point flexure strength through the use of Weibull strength size-scaling. This size-scaling can be used to predict and compare the strength of a material even when different specimen sizes or test configurations are used. The measured three-point flexure strength and the value predicted by size-scaling are shown in Table 3. The predicted and measured values are in agreement considering the limited number of experiments; individual results are plotted in Fig. 6 and give a sense of the scatter in the data.

Table 3 Summary of α-SiC flexural strengths

Fig. 6

Flexural strengths for SiC-α for different beam geometries and strain-rates. Low-rate results were obtained from a screw-driven load frame and the high-rate results from the Kolsky bar method

High-Rate Experiments

The results of several high-rate experiments on α-SiC are now presented. The first is given in some detail to illustrate the full analysis. This experiment used 3.18 mm diameter output bars and specimen geometry B (25 mm length, 20 mm span, low moment-of-inertia). As mentioned above, it was desired to aim for a strain-rate of 10/s, about 10⁶ times larger than that achieved in the low-rate tests. This seemed reasonable based on the numerical results. For this experiment, it required the tapered striker described above, an impact speed of 14.5 m/s and a 1.0 mm length of aluminum wire as a shaper. The strain-gage output is shown in Fig. 7, SG1 denotes the input bar gage, and SG2a and b the output bar gages.

Fig. 7

Strain gage measurements from an experiment at 10/s, beam geometry B, and 3.18 mm diameter output bars

The ramp loading of the incident pulse (SG1) is due to the pulse shaping/tapered striker. The initial part of the reflection (SG1, starting at about 0.55 ms) is compressive, in contrast to most Kolsky bar experiments, because of the low-impedance input bar. Again, this results in good measurements of F ₁. The transmitted pulses (SG2a and SG2b) are very similar due to the symmetry of the experiment, and are difficult to differentiate in the figure. The next step in the analysis is to translate the incident, reflected, and transmitted pulses in time to the instant they act at the roller interfaces (accounting for dispersion). These are shown in Fig. 8.

Fig. 8

Strain signals after dispersion correction

On this time-base, the failure occurs at approximately 0.44 ms which is clear in both the reflected pulse and the transmitted pulses.³ From these signals, forces F ₁ and F ₂ can be determined from Eqs. 4–6. These are plotted in Fig. 9. Similar trends were observed in the simulations. The output bar measurements initially lag the input bar measurement due to the time the wave takes to travel from the input bar through the specimen and to the output bars. The input bar force, F ₁, exceeds that of the output bars, F _2a and F _2b , by an amount consistent with what would be expected due to inertia in this case (approximately 20 N). The absence of large oscillations in the force suggests that wave effects within the sample are not a problem. In this situation, peak force is best estimated from the average of the peak force measurements, i.e., $P = \frac{1}{2}\left[ {F_{1} + \left( {F_{2a} + F_{2b} } \right)} \right]$

Fig. 9

Force versus time for the three measurements made from the data in Fig. 8

Figure 10 is a plot of the measured forces with beam deflection, δ, determined by Eq. (11) assuming negligible roller deformation (infinite k _R ) against time. The ideal behavior, Eq. (1) is also plotted. The measured deflections deviate from the ideal case, with the beam appearing more compliant than expected. This is partially explained by roller compliance, which can be included in Eq. (1). Assuming a roller deflection of 75 MN/mm, as estimated from the simulations, this is represented as the lower slope dashed curve in the figure (labeled “w/k _R ”). However, this does not completely remove the discrepancy. This error is considered to be minor, as the Kolsky bars are optimized for the accurate measurement of force, not deflection, and beam deflection is irrelevant to the calculation of flexural strength. However, a strain-rate must be reported with each flexural strength measurement, and there are two ways to do this: (1) based on beam deflection measured by the bars, essentially Eq. (11) but using a possibly imperfect estimate for roller deformation, or (2) by relating strain to measured load in Eq. (2). The latter method was chosen, and strain-rate for this experiment using this method is shown in Fig. 10. The downside of this method is that, using an averaged force for the load in Eq. (2), it is not valid for early times when wave propagation is still significant. This leads to a rise in the strain-rate which is probably not representative of the actual strain-rate at the fracture location. This is seen in Fig. 10, up until approximately 0.007 mm of deflection has been achieved.

Fig. 10

Load deflection curves for the experiment at ~10/s, beam geometry B, and 3.18 mm output bars

As predicted by the simulations, the inertial effects can be reduced by increasing the output bar diameter to 6.35 mm while keeping the beam geometry and applied strain-rate the same (approximately 9/s). The same striker and shaper were used, but with a lower impact speed of 11 m/s. The measured forces are plotted with time for this experiment in Fig. 11. Better agreement between the forces is obtained, indicating that the inertial term has been reduced.

Fig. 11

Forces measured by an experiment with a 20 mm span and 6.35 mm output bars. This specimen was unloaded without fracture

Note that fracture did not occur in this experiment; the specimen was loaded and unloaded elastically and recovered, and it is interesting to observe both the loading and unloading. This can be seen in Fig. 12 which plots force with displacement, where displacement is determined from the Kolsky bar analysis as before. Like the previous experiments, the beam appears less stiff than that predicted by the ideal solution, even when a compliance correction is made. What is more interesting is that the unloading path does not exactly match that of the loading. It is unlikely that this is due to material behavior of the ceramic. Other possibilities include small-scale plastic deformation of the rollers, slight misalignment, inelastic behavior in the epoxy adhesive used to attach the rollers to the bar, small mis-calibrations of the strain-gages used for instrumentation, or even creep in the gage glue bonds. Again, this error is small, but it is emphasized that because of this discrepancy it is best to estimate strain-rate from the measured force.

Fig. 12

Forces and strain-rate for an experiment with a 20 mm span, low moment-of-inertia, and 6.35 mm output bars

Additional high-rate experiments were conducted with α-SiC. The results are presented along with the low-rate data in Fig. 6. Also included in the data are experiments in the high-moment of inertia orientation (geometry C), which, given the scatter in the data overall, are consistent with data from the other geometries.

Discussion and Conclusion

In this paper a method has been outlined and validated to perform high-rate 3-point bend experiments with a three-bar Kolsky bar to determine the high-rate flexure strength of ceramic materials. In this approach, flexure strength is determined through the measurement of loading-point-force at the instant of fracture. Standard elementary beam theory is used to relate force to fracture stress, i.e., Eq. (2). This requires that the assumptions inherent in this equation are valid, e.g., linear elastic behavior, small deflections/curvature, and quasi-static loading. Standardized geometries have been established for low-rate experiments to meet these requirements, but may not be valid at high rates due to the difficulties in achieving equilibrium in a high-rate experiment. Thus it is reasonable to re-evaluate established standards with equilibrium issues in mind. Clearly, equilibrium can be improved by using shorter span/length specimens with higher moments of inertia than those specified in the standard. Finite element analysis was used to validate this, and in general is an ideal method to explore various specimen geometries and loading conditions to produce beam behaviors that fall within the assumptions implicit in the elementary theory.

Based on the simulation results, we were able to distinguish between two “types” of equilibrium. The first is related to whether or not the wave propagation within the beam was negligible for a given loading, and was evident as large oscillations in the force measurements. The second is due to the “rigid body” acceleration of the beam. We use this term because even a perfectly rigid beam, by definition always in equilibrium, will produce inertial errors in the force measurements due to its acceleration when loaded as done here. This basic error can largely be accounted for by simply averaging the forces measured by each bar. Alternately, it can be reduced (without reducing the strain-rate) by increasing the diameter (and stiffness) of the output bars. This can be done to the point at which we lose fidelity in the F₂ force measurement, which decreases as output bar stiffness increases. These findings were confirmed experimentally with experiments on α-SiC.

Equilibrium was confirmed experimentally by comparing force measurements at the loading points. A “thin” input bar was used to obtain good measurements of F₁, which typically causes problems when testing weak samples. This was a primary consideration in the design of the Kolsky bar (materials and dimensions). We also found that since the specimen behavior is known (linear elastic to fracture, for which a good estimate of the fracture strength is available), much of the experiment could be anticipated in advance and the apparatus could be designed around the behavior of the samples using well-known relationships. More specifically, it was possible to determine a precisely ramped incident pulse that would load a given sample in the manner desired.

Efforts next focused on determining an experimental method to generate these incident pulses. Pulse shaping is a valuable technique on which much has been written. Our use of “compliant” bars increases the sensitivity of the specimen response to the incident pulse profile. This is because the bars are more influenced by the comparatively stiff sample. Simple deformable wave shapers, which may produce adequate load shapes in stiffer Kolsky bar arrangements without much difficulty, could not be found to produce the necessary pulses here. We found that much more flexibility could be obtained by using deformable shapers with tapered strikers. A single tapered striker was then designed using a basic explicit finite element analysis described in the Appendix. Simulations were performed iteratively where striker shape was varied until an adequate shape was determined that would produce incident pulses that approximately matched those required by Eq. (11), in conjunction with available pulse-shapers, for a range of testing conditions. One-dimensional analyses were used for speed and simplicity, and the resulting striker was made from polycarbonate to simplify machining. Note this approach could be used for more general Kolsky bar testing.

The experimental methods were demonstrated with α-SiC. Figure 6 presents a preliminary dataset for this material, using different geometries and at different loading rates. The low-rates are approximately 0.000002/s, and the high-rate approximately 10/s. Considering the scatter in the data, no strain-rate effect is clearly evident. Note also that although the Kolsky bar experiments are at a much higher strain-rate than those conducted in the load-frame, they are still not extraordinarily high. It may be possible to determine flexure strength at higher rates by using smaller specimens, essentially using the approaches outlined above. The 2 × 3 × 25 mm specimen described in ASTM C1161 could serve as a good starting point.⁴ These methods may also be useful for the determination of fracture toughness at high-rates, using for example, pre-cracked beams. This is one reason why we have opted to not use direct measurements of flexure strength with strain-gages mounted directly on the specimens; strain gage instrumentation becomes more difficult with smaller specimens or with specimens that contain pre-cracks or notches.

In some cases it is an advantage to use 4-point bending rather than 3-point. If a method could be devised to load two input bars simultaneously, or if two rollers with a very short span could be adapted to the incident bar, an analogous approach to that used here would be possible. From our preliminary simulations, not presented here, there does not seem to be an inherent advantage to using either 3 or 4 point bending from an equilibrium standpoint, although this has not been investigated fully for a variety of possible loading conditions.

Appendix

The following is a description of the explicit, Lagrangian, finite element method used to design the variable impedance (tapered) striker described in this paper.⁵ It is based on the uniaxial strain approach described in [24], and has been adapted to the one-dimensional stress conditions of the Kolsky bar. It is intentionally simple to minimize computation time and allow the rapid design of projectile shapes using a “trial-and-error” approach. It can be generalized to accommodate other one-dimensional stress problems but here it is described to solve the specific case of a tapered striker impacting a wave-shaper with known mechanical response and backed by a uniform input bar. The output is the incident pulse generated by this impact, which can be compared to a desired pulse, for example predicted by Eq. (17).

An example mesh is shown in Fig. 13. The striker has length L_S and consists of N_S linear elastic elements, each with density ρ_S and elastic modulus E_S. Similarly, the input bar has length L_I, consists of N_I linear elastic elements, each with density ρ_I and elastic modulus E_I. The striker and input bar are uniformly divided into elements, so that each element in the striker has length δL_S = L_S/N_S and each element in the input bar has length δL_I = L_I/N_I. The cross-sectional area of the input bar is assumed constant, i.e., each input bar element has an area of A_I. Each element in the striker, however, can be assigned its own individual area, A_S,j for j = 1, N_S. Thus a taper can be represented with reasonable accuracy provided the area changes between neighboring elements are not too large.

Fig. 13

An example mesh used to design the striker. Elements are labeled below the mesh; nodes are labeled above

The wave-shaper is represented by a single element between the striker and input bar as shown in Fig. 13. Since we are not concerned with wave-propagation or non-uniform deformation in the shaper, this description is adequate. Contact between the wave-shaper and striker is important to avoid the transmission of unrealistic tension into the input bar; in most cases the input bar and striker will separate and the contact algorithm will allow them to do so. One contact interface is sufficient here, and the physical implication that the shaper “sticks” to the input bar, because of the shared node, is of little practical consequence.

The mechanical behavior of the wave-shaper is treated as elastic–plastic. This behavior is input in terms of the force applied to the shaper (F_W) and its total deformation (δ_W), both positive in compression. The total deformation is written as the sum of the elastic and plastic components, i.e., δ_W = δ_W,e + δ_W,p. The elastic response is governed by a spring constant k_W (input), and the plastic response by an exponential hardening rule

$$ F_{W} = A + B\delta_{W,p}^{n} . $$

(18)

The shaper response could be described in terms of stress and strain, however, this approach permits the use of shapers that may not be uniform in cross-section, as will be shown below. Shaper area is irrelevant because of the formulation in terms of force. Shaper length and mass are defined as L_W and m_W.

Elements and nodes are labeled sequentially from left to right. Initial nodal positions, for each node j, are given by the following.

$$ x_{0,j} = \left\{ {\begin{array}{*{20}l} {\left( {j - 1} \right)\delta L_{S} } \hfill & {j \in \left[ {1, N_{S} + 1} \right]} \hfill & \,\,\,\,\,{(stiker\,bar)} \hfill \\ {\begin{array}{*{20}c} {L_{S} } \\ {L_{S} + L_{W} } \\ \end{array} } \hfill & {\begin{array}{*{20}c} {j = N_{S} + 2} \\ {j = N_{S} + 3} \\ \end{array} } \hfill & {\begin{array}{*{20}c} {(1st\,node\,of\,shaper)} \\ \,\,\,\,{(1st\,node\,of\,input\,bar)} \\ \end{array} } \hfill \\ {\left( {L_{S} + L_{W} } \right) + \left( {j - N_{S} - 3} \right)\delta L_{I} } \hfill & {j \in \left[ {N_{S} + 4, N_{S} + 3 + N_{I} } \right]} \hfill &\,\,\,\,\,\,{(remaining\,input\,bar)} \hfill \\ \end{array} } \right. $$

(19)

Element masses are lumped to the nodes. The masses of the nodes are as follows.

$$ m_{0,j} = \left\{ {\begin{array}{*{20}l} {\delta L_{S} A_{S,j} \rho_{S} /2} \hfill & {j = 1} \hfill & {(1st\,node\,of\,striker)} \hfill \\ {\delta L_{S} \rho_{S} \left( {A_{S,j - 1} + A_{S,j} } \right)/2} \hfill & {j \in \left[ {2, N_{S} } \right]} \hfill & {(interior\,striker\,nodes)} \hfill \\ {\delta L_{S} A_{S,j} \rho_{S} /2} \hfill & {j = N_{S} + 1} \hfill & {(last\,node\,of\,striker)} \hfill \\ {m_{W} /2} \hfill & {j = N_{S} + 2} \hfill & {(1st\,node\,of\,shaper)} \hfill \\ {(\delta L_{I} A_{I} \rho_{I} + m_{W} )/2} \hfill & {j = N_{S} + 3} \hfill & {(1st\,node\,of\,input\,bar)} \hfill \\ {\delta L_{I} A_{I} \rho_{I} } \hfill & {j \in \left[ {N_{S} + 4, N_{S} + 2 + N_{I} } \right]} \hfill & {(interior\,input\,bar\,nodes)} \hfill \\ {\delta L_{I} A_{I} \rho_{I} /2} \hfill & {j = N_{S} + 3 + N_{I} } \hfill & {(last\,node\,of\,input\,bar)} \hfill \\ \end{array} } \right. $$

(20)

A uniform initial velocity is assigned to the striker nodes. All other nodes are initially stationary.

$$ v_{0,j} = \left\{ {\begin{array}{*{20}l} {v_{impact} } \hfill & {j \in \left[ {1, N_{S} + 1} \right]} \hfill \\ 0 \hfill & {j \in \left[ {N_{S} + 2, N_{S} + 3 + N_{I} } \right]} \hfill \\ \end{array} } \right. $$

(21)

The solution is obtained by integrating the equations of motion in time. A time step is chosen using the Courrant condition, which states that the time step must be smaller than the smallest time needed for an elastic wave to travel the length of an element. The wave-speed in the striker and input bar are $c_{S} = \sqrt {E_{S} /\rho_{S} }$ and $c_{I} = \sqrt {E_{I} /\rho_{I} }$. A wave speed for the wave-shaper can be defined by $c_{W} = \sqrt {k_{W} L_{W} /m_{W} }$. Transit times can easily be found from the element lengths, and the final time step is then given by

$$ \delta t = S \cdot \hbox{min} \left( {\frac{{\delta L_{S} }}{{c_{S} }},\frac{{\delta L_{I} }}{{c_{I} }},\frac{{L_{W} }}{{c_{W} }}} \right) $$

(22)

where S must be less than one for stability. S = 0.7 is a typical value, and is used below. The time step in general will change as the simulation progresses because of the deformation of the elements, especially the inelastic shaper which may deform considerably.

Nodal accelerations, velocities, and displacements at time t are determined from the values at the previous time step. Initially, the forces are all zero.

$$ a_{j}^{t} = \frac{{F_{j}^{t - \delta t} }}{{m_{j} }} $$

(23)

$$ v_{j}^{t} = u_{j}^{t - \delta t} + v_{j}^{t - \delta t} \delta t $$

(24)

$$ u_{j}^{t} = u_{j}^{t - \delta t} + v_{j}^{t - \delta t} \delta t $$

(25)

At this point, contact must be checked to determine if there is interference between the striker and shaper. If there is no interference between the contact nodes N_S + 1 and N_S + 2, no adjustment is needed. If there is interference, i.e., if u ^t _Ns+1  > u ^t _Ns+2 , then both nodal positions are updated to the center of mass.

$$ u_{cm}^{t} = \frac{{u_{Ns + 1}^{t} m_{Ns + 1} + u_{Ns + 2}^{t} m_{Ns + 2} }}{{m_{Ns + 1} + m_{Ns + 2} }} $$

(26)

Element strain is determined from the new element lengths, and stress in the elastic elements can be found from Hooke’s law.

$$ \epsilon_{j}^{t} = \left\{{\begin{array}{*{20}c} {\left({u_{j + 1}^{t} - u_{j}^{t}} \right)/\delta L_{S}} & {j \in \left[{1, N_{S}} \right]} &{(striker\,elements)} \\ {\left({u_{j + 2}^{t} - u_{j + 1}^{t}} \right)/\delta L_{I}} & {j \in \left[{N_{S} + 2, N_{S} + 1 + N_{I}} \right]} &\,\,\,\,{(input\,bar\,elements)} \\ \end{array}} \right. $$

(27)

$$ \sigma_{j}^{t} = \left\{{\begin{array}{*{20}c} {E_{S} \epsilon_{j}^{t}} & {j \in \left[{1, N_{S}} \right]} & {(striker\,elements)} \\ {E_{I} \epsilon_{j}^{t}} & {j \in \left[{N_{S} + 2, N_{S} + 1 + N_{I}} \right]} &\,\,\,\, {(input\,bar\,elements)} \\ \end{array}} \right. $$

(28)

Force in the shaper is determined by radial return. An initial force is calculated assuming the increment of deformation in a given time step is elastic. If this trial stress exceeds the current flow condition, given by Eq. (18), the stress is assigned the current flow force, and the plastic deformation is updated. Nodal forces are finally determined from the bar-element stresses and the wave-shaper force, depending on which elements act on a particular node. These are then used as input to the next time step, starting at Eq. (23).

$$ F_{j}^{t} = \left\{ {\begin{array}{*{20}l} {\sigma_{j}^{t} A_{S,j} } \hfill & {j = 1} \hfill & {(1st\,node\,of\,)} \hfill \\ { - \sigma_{j - 1}^{t} A_{S,j - 1} + \sigma_{j}^{t} A_{S,j} } \hfill & {j \in \left[ {2, N_{S} } \right]} \hfill & {(interior \,striker\,nodes)} \hfill \\ { - \sigma_{j - 1}^{t} A_{S,j - 1} } \hfill & {j = N_{S} + 1} \hfill & {(last\,node\,of\,striker)} \hfill \\ { - F_{W} } \hfill & {j = N_{S} + 2} \hfill & {(1st\,node\,of\,shaper)} \hfill \\ {(\sigma_{j - 1}^{t} A_{I} + F_{W} )} \hfill & {j = N_{S} + 3} \hfill & {(1st\,node\,of\,input\,bar)} \hfill \\ { - \sigma_{j - 2}^{t} A_{I} + \sigma_{j - 1}^{t} A_{I} } \hfill & {j \in \left[ {N_{S} + 4, N_{S} + 2 + N_{I} } \right]} \hfill & {(interior \, input\,bar\,nodes)} \hfill \\ {\sigma_{j - 2}^{t} A_{I} } \hfill & {j = N_{S} + 3 + N_{I} } \hfill & {(last\,node\,of\,input\,bar)} \hfill \\ \end{array} } \right. $$

(29)

An example application is now shown. This application is intended to show that this method can accurately predict the incident pulse generated by the impact of a tapered striker with a deformable wave-shaper. The more general application suggested here is as a tool to design a tapered striker that can fine-tune the incident pulse created by any given wave-shaper. This can provide more flexibility in the incident pulse shapes that can be achieved, and is a self-explanatory extension of that described here.

The finite element method described above was implemented into the commercially available Microsoft Excel. The response of the desired wave-shaper must be known beforehand, and in this case was determined from a previous Kolsky bar experiment. The wave-shaper was a 1.0 mm length of 1 mm diameter 99.999 % pure aluminum wire, loaded diametrically. This response is shown in Fig. 14, along with the fit input to the code. The polycarbonate striker and aluminum input bar are described in the main text, and their properties are also input to the code. The shape of the striker is shown in Fig. 15. In this case, N_S = 50 and N_I = 100. Using a standard desktop PC the solution is computed instantaneously for all practical purposes. This allows the effect of user-changes to shaper geometry to be calculated rapidly.

Fig. 14

Response of the wave-shaper—experimentally measured along with the curve fit used in the finite element analysis

Fig. 15

Shape of projectile used in the finite element analysis

The incident pulse predicted by the code for an impact speed of 15.5 m/s is shown in Fig. 16, along with an experimentally measured pulse at this same speed. The agreement along the loading portion is excellent although there is some deviation during the unloading process. This can be due to variability in wave-shapers, or an imperfect fit to the unloading response of the shaper.

Fig. 16

Incident pulse resulting from a tapered striker and an aluminum wire wave shaper—experiment compared to that predicted by the finite element analysis