Spatial feedbacks and the dynamics of savanna and forest

Abstract

Theoretical models and empirical analyses have combined to suggest that, for some ranges of climate, alternative stable states in vegetation structure may be possible: positive feedbacks with fire may differentiate savanna from forest, while positive feedbacks with hydrological processes may differentiate grassland from savanna. However, existing models have largely failed to include spatially explicit fire spread, dispersal, and hydrological processes, and as such ignore key features of vegetation systems. In this paper, we incorporate spatial and stochastic effects to form a comprehensive and realistic description of the dynamics of vegetation growth. By using novel computational tools such as path-sampling, we investigate the effect of noise and spatial coupling on the stability and the dynamics of forest-savanna transitions. Spatial effects change model behaviors: We find that spatial interactions between savanna and grassland result in the eventual nucleation and propagation of one of the states to invade the other. Which state wins depends on parameter values, which in turn depend on environmental conditions. Meanwhile, transitions between savanna and forest occur much less frequently, because an event such as a period of fire suppression in savanna or a fire in forest must be larger to successfully invade a landscape; this results in transitions between savanna and forest that, although not strictly history dependent, look temporally similar to hysteresis because the time lags involved in transitions are so large.

Appendices

Appendix 1. Detailed stability analysis of the well-mixed model

In this section, we analyze in detail the well-mixed or mean-field model considered in this paper. To simplify the subsequent analytical computations, some results will be presented as asymptotic in δ, which we assume throughout this work to be small. Note that non-asymptotic analytical computations can always be carried out, but it gets cumbersome to write down the full expressions.

Consider the well-mixed model (μ = ν = 1)

$$ \begin{array}{@{}rcl@{}} \dot{T} & = & - T+ w S h(T), \\ \dot{S} & = & - S+(\delta+\beta T^{2})\left( 1-T-S\right)- w S h(T). \end{array} $$

(19)

To obtain steady states, we set $\dot {T}=\dot {S}=0$ to get

$$ \begin{array}{@{}rcl@{}} 0 & = & -T+w S h(T), \\ 0 & = & -S+(\delta+\beta T^{2})\left( 1-T-S\right)- w S h(T). \end{array} $$

(20)

which simplifies to

$$ w h(T)=K(T):= \frac{T \left( \delta +\beta T^{2}+1\right)}{\delta -T (\delta +\beta (T-1) T+1)}. $$

(21)

Let us assume that β is sufficiently large so that K(T) has only one asymptote, i.e., the numerator of K(T) has only one zero. This is equivalent to the condition that the discriminant of the cubic polynomial δ − T(δ + β(T − 1)T + 1) is negative, which implies

$$ \begin{array}{@{}rcl@{}} \beta >& \frac{ 1 + 20 \delta - 8 \delta^{2} + \sqrt{1 -24 \delta + 192 \delta^{2} -512 \delta^{3}} } {8 \delta } \\ =& \frac{1}{4 \delta } + 1 + \mathcal{O}(\delta). \end{array} $$

(22)

In this case, the only asymptote of K(T) is at

$$ \begin{array}{@{}rcl@{}} T_{\text{asymp}} = \frac{1}{2} \left( 1 + \sqrt{1 - 4/\beta} \right) + \mathcal{O}(\delta). \end{array} $$

(23)

One can check that T_asymp < 1 and approaches 1 as β →∞. Therefore, K(T) > 0 for T ∈ [0,T_asymp) and K(T) < 0 for T ∈ [T_asymp, 1]. Consequently, wh(T) can only intersect K(T) in the range [0,T_asymp). The number of intersections depends on the behavior of K(T): if K(T) is monotone increasing in [0,T_asymp), then there is only one intersection; if K(T) has turning points in [0,T_asymp), there can be multiple intersections. See Fig. 1. To investigate turning points, we set K^′(T) = 0 to yield the equation

$$ \delta (\delta +1)+\beta^{2} T^{4}+\beta (2 \delta -1) T^{2}=0, $$

(24)

whose solutions are

$$ \begin{array}{@{}rcl@{}} T_{1} &=& \sqrt{\frac{1-2\delta - \sqrt{1-8 \delta}}{2\beta }}, \end{array} $$

(25)

$$ \begin{array}{@{}rcl@{}} T_{2} &=& \sqrt{\frac{1-2\delta + \sqrt{1-8 \delta}}{2\beta }}. \end{array} $$

(26)

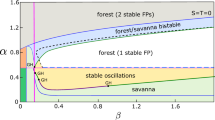
If δ > 1/8, these solutions are complex and consequently, K has no turning points for T ∈ [0, 1]. Alternatively δ < 1/8, where T₁,T₂ ∈ [0, 1]. In particular, T₁ is a local maximum and T₂ is a local minimum of K. For δ = 1/8, T₁ = T₂ is a point of inflection. We shall hereafter assume that δ < 1/8 so that there is a possibility, as we subsequently demonstrate, of producing up to 3 stable steady states. Lastly, we require T₂ < 0.4 in order to produce two low-coverage (< 40% tree coverage) steady states, which translates to the condition

$$ \begin{array}{@{}rcl@{}} \beta>\frac{25}{8} \left( 1 -2 \delta +\sqrt{1-8 \delta }\right). \end{array} $$

(27)

We also assume that the two conditions (22), (27) on β are satisfied.

To analyze stability of the steady states, we investigate the eigenvalues of the Jacobian matrix, which for T≠ 0.4 is

$$ \begin{array}{@{}rcl@{}} J(T,S) := \left( \begin{array}{cccc} -1 & w h(T) \\ \!\!-\beta T^{2} + 2 \beta T (1 - S - T) - \delta & -\beta T^{2} - w h(T) - \delta - 1 \end{array}\!\! \right)\!\!\!\!\!\!\\ \end{array} $$

(28)

We have

$$ \begin{array}{@{}rcl@{}} \text{Trace}[J(T,S)] &=& -\delta - w h(T) - \beta T^{2} - 2 < 0 \end{array} $$

(29)

$$ \begin{array}{@{}rcl@{}} \text{Det}[J(T,S)] &=& \delta + \beta T^{2} + 1 + w h(T)\\ &&(\delta + \beta T(2 S + 3 T - 2)+1). \end{array} $$

(30)

Since the trace (which is equal to the sum of the eigenvalues) is negative, at least one of them must have negative real part. The sign of the real part of the other eigenvalue then determines the stability of the steady state. In particular, if the determinant (which is equal to the product of eigenvalues) is positive, then the steady state is stable. If it is negative, we then have an unstable saddle point. Eliminating S at a steady state, we have

$$ \begin{array}{@{}rcl@{}} \text{Det}[J(T)] &\equiv& Det[J(T, T/wh(T))] \\ &=& 1 + \beta (\delta + 2 {h(T)}^{2}) T^{2} + w h(T)\\ &&(1 + \delta +\beta T (3T - 2)). \end{array} $$

(31)

First, we investigate the stability of T_grassland, the steady state with the smallest T value. This exists as long as w < K(T₁), and must satisfy T_grassland < T₁ and so h(T_grassland) = 1. In particular, T_grassland solves w = K(T_grassland) and admits the asymptotic expression

$$ \begin{array}{@{}rcl@{}} T_{\text{grassland}} = \frac{w}{1+w} \delta + \mathcal{O}(\delta^{2}). \end{array} $$

(32)

This gives $\text {Det}[J(T_{\text {grassland}})] = 1+w + \mathcal {O} (\delta )$, which is positive for small δ. Hence, T_grassland is stable. Similarly, T_savanna is the largest real solution distinct from T_grassland of w = K(T_savanna). This gives

$$ \begin{array}{@{}rcl@{}} T_{\text{savanna}} = \frac{\sqrt{\beta} w + \sqrt{\beta w^{2} - 4{(1+w)}^{2}}}{2 (1+w)} + \mathcal{O}(\delta), \end{array} $$

(33)

which is real if $w > w_{1} = 2(2+\sqrt {\beta })/(\beta -4) + \mathcal {O}(\delta )$. Hence,

$$ \begin{array}{@{}rcl@{}} \text{Det}[J(T_{\text{savanna}})] &=& \frac{\beta w^{2}+\sqrt{\left( \beta w^{2}\right)^{2}-4 (w+1)^{2} \left( \beta w^{2}\right)}} {2 (w+1)}\\ &&-2 (w+1) + \mathcal{O}(\delta) \end{array} $$

(34)

is positive to leading order in δ. This establishes the stability of T_savanna. Note that by a similar calculation, the solution of w = K(T) between T_grassland and T_savanna is given by

$$ \begin{array}{@{}rcl@{}} T = \frac{\sqrt{\beta} w - \sqrt{\beta w^{2} - 4{(1+w)}^{2}}}{2 (1+w)} + \mathcal{O}(\delta), \end{array} $$

(35)

which one can check is a saddle point with Det[J(T)] < 0. Finally, T_forest is obtained as the largest real solution of 1.2w = K(T) that also satisfies T > 0.4. This has the asymptotic expression

$$ \begin{array}{@{}rcl@{}} T_{\text{forest}} = \frac{3 \beta w + \sqrt{9 \beta^{2} w^{2}-\beta (6 w+5)^{2}}}{\beta (6 w+5)} + \mathcal{O}(\delta), \end{array} $$

(36)

and it is real and greater than 0.4 if $w>w_{2} = 1.2(4\beta +25)/(6\beta - 25) + \mathcal {O}(\delta )$. As before, one can check that in this case, DetJ(T_forest) > 0 and so T_forest is stable. This tri-stable situation persists until w > K(0.4), i.e., $w > w_{3} = (4\beta +25)/(6\beta -25) + \mathcal {O}(\delta )$, after which T_savanna > 0.4 and thus is no longer an allowed steady state. Finally, T_grassland also vanishes when w > w₄ = K(T₁), after which we are left with a unique stable steady state T_forest.

Appendix 2. The effect of noise and spatial coupling on multi-stability

In this section, we discuss through a concrete 1D example the effect of noise and spatial coupling on multi-stable dynamical systems. Fix an unequal double-well potential $V(u) = \tfrac {1}{2}{(u-1)}^{2}{(u+1)}^{2} + \delta u$ where |δ|≪ 1. The potential V (u) has two local minima u₊,u₋ close to ± 1 and the global minimum is u₊ (resp. u₋) if δ < 0 (resp. δ > 0). Consider the 1D dynamical system given by the gradient flow

$$ \begin{array}{@{}rcl@{}} \dot{u} = - V^{\prime}(u). \end{array} $$

(37)

It is clear that for any initial condition except the saddle point of V, u converges to either u₊ or u₋, depending on the initial condition. In other words, the system is bistable in the sense that there are two stable equilibrium points of the dynamics. One can impart a dynamical meaning to this bistability by considering the noisy version of Eq. 37,

$$ \begin{array}{@{}rcl@{}} \dot{u} = - V^{\prime}(u) + \sqrt{2\sigma} \eta, \end{array} $$

(38)

where η is a 1D white noise and σ ≪ 1. In this case, most of the time u is close to one of u_±, but it occasionally jumps between them. The rate of jumping is determined by V and in particular, one can check that the invariant (equilibrium) distribution of u is

$$ \begin{array}{@{}rcl@{}} \rho(u) \propto \exp(-V(u) / \sigma). \end{array} $$

(39)

Hence, with the small noise, the system is bistable in the true dynamical sense and one can talk about transition events between u_±, which is not possible in Eq. 37 whose evolution is entirely determined by its initial condition.

Fig. 16

The evolution of Eq. 41 with an initialized front between alternative stable states of the well-mixed model. We took r = 10,σ = 1e − 2, and n = 100. Instead of bistability, we observe propagating fronts that selects u₋ over u₊ effectively deterministically. The bistability decays in the thermodynamic limit

The addition of spatial coupling fundamentally changes the bistable picture described above. Let us consider n copies of the dynamics (37) with a spatial coupling in the form

$$ \begin{array}{@{}rcl@{}} \dot{u}_{i} &=& - V^{\prime}(u_{i}) + r (u_{i+1} - 2u_{i} + u_{i-1}) + \sqrt{2\sigma} \eta_{i},\\ i&=&1,2,\dots,n \end{array} $$

(40)

where periodic boundary conditions u_n+ 1 ≡ u₀ and u_− 1 ≡ u_n are enforced. Let us also define the macrostate $\bar {u}$ as the spatial average $\bar {u}:=\tfrac {1}{n} {\sum }_{i=1}^{n} u_{i}$. Evidently, if every u_i = u₊ (or u₋) then the coupling term vanishes and one is tempted to conclude that $\bar {u}$ behaves like the well-mixed model (38). However, this is not the case, especially in the limit n →∞.

Suppose that we initialize the systems so that all of u_i(0) = u₋ except for a interval of values where u_i(0) = u₊. Although the interior of each of these clusters will fluctuate stably around either u₊ or u₋, the interfaces between them will move deterministically depending on the sign of δ. For example, if δ > 0 (no matter how small), the interface will move in such a way as to destroy the cluster of states with values equal to u₊. This is known as “propagation.” This will happen as long as a “nucleation” event happens, i.e., there is a sufficiently large cluster of u_i such that u_i = u₋ so that a well-defined interface is formed. Once formed, the propagation effect will take over the system. The smallest size m of the nucleus required is called the critical nucleus size. It can be shown that m the transition u₊ → u₋ is independent of n for δ > 0, whereas the critical nucleus size of the reverse transition grows linearly in system size (this must be the case since these critical nuclei are complement of each other). See for example, Vanden-Eijnden and Westdickenberg (2008) and Weinan et al. (2012) for concrete analysis of such phenomena.

Hence, spatial coupling introduces a fundamental asymmetry between macrostates $\bar {u} = u_{+}$ and $\bar {u} = u_{-}$ for δ≠ 0 that manifests itself in the thermodynamic limit n →∞. If δ > 0, then the transition from $\bar {u} = u_{+}$ to $\bar {u} = u_{-}$ requires only a cluster of m (independent of n) u_i’s to jump to u₋, and this happens with probability approaching 1 as n grows due to the random fluctuations. On the other hand, the reverse transition requires n − m clusters to be formed due to random fluctuations. This probability of this happening per unit time has leading exponential form κ^n−m (where κ is the rate per unit time of each patch jumping). This decays exponentially as n →∞. The reverse case is true for δ < 0. Hence, δ = 0 can be regarded as a well-defined first-order phase transition point of the spatial system in the thermodynamic limit, where the macrostates u_± exchange relative stability.

These effects highlight the difference between phase transition in spatial systems and bistability in mean-field systems.

Appendix 3. Free action and its computation

In this section, we give a formal introduction to the concept of free action, which can be thought of as a non-equilibrium analogue of the free energy for studying transition dynamics in non-equilibrium systems. The reader is referred to Li and Weinan (2015) for a more complete exposition.

C.1 The general microscopic model

Consider a system of over-damped Langevin equations for x(t) = (x₁(t),…,x_n(t)) in the form

$$ \begin{array}{@{}rcl@{}} \dot{x}_{i}(t) = f_{i}(x(t)) + \sqrt{2\sigma} \eta_{i}(t) \qquad i = 1, 2, \dots, n \end{array} $$

(41)

where $x_{i}(t) \in \mathbb {R}^{d}$, $f_{i} : \mathbb {R}^{d}\rightarrow \mathbb {R}^{d}$ and η_i(t) are d-dimensional white noises. The equation is interpreted in the Itô sense and n is the system size. We hereafter denote f = (f₁,…,f_n). Let us also denote by ρ_n the invariant distribution of x(t), which exists under mild conditions, e.g., if there exists R > 0 such that x^Tf(x) < − 1/R for all x such that |x| > R (Khasminskii 2011). The invariant distribution ρ_n can be shown to satisfy the stationary Fokker-Planck equation

$$ \begin{array}{@{}rcl@{}} - \nabla \cdot (f(x) \rho_{n}(x)) + \sigma \triangle \rho_{n}(x) = 0. \end{array} $$

(42)

In particular, if we are considering an equilibrium (or gradient) system with f = −∇V for some potential function $V:\mathbb {R}^{d\times n} \rightarrow \mathbb {R}$, then we have

$$ \begin{array}{@{}rcl@{}} \rho_{n}(x) \propto e^{-\frac{1}{\sigma} V(x)}. \end{array} $$

(43)

We shall consider the case where there need not exist such a potential function, i.e., the system is not an equilibrium or gradient one. This is in fact the case for the dynamical model for savanna-forest transitions considered in this paper. Nevertheless, the invariant distribution ρ_n may still exist.

C.2 Macrostates and relative stability

We are typically interested in macroscopic observations of x. To this end, let us define a macrostate z = ϕ_n(x) where $\phi _{n} : \mathbb {R}^{d\times n} \rightarrow \mathbb {R}^{l}$ where l is small and in particular, independent of the system size n. For example, we may take z to be the spatial average of x by setting $z=\phi _{n}(x)\equiv \tfrac {1}{n} {\sum }_{i} x_{i}$, in which case l = 1. The invariant distribution of the stochastic process z(t) = ϕ_n(x(t)) is formally given by the integral

$$ \begin{array}{@{}rcl@{}} p_{n}(z) = {\int}_{\mathbb{R}^{d\times n}} \delta(\phi_{n}(x) - z) \rho_{n}(x) dx, \end{array} $$

(44)

where δ is the Dirac delta function.

Our goal is come up with a notion of relative stability of different values of the macrostate z in the thermodynamic limit n →∞. In equilibrium or gradient systems, this can be done by simply defining the free energy$F:\mathbb {R}^{l} \rightarrow \mathbb {R}$ by

$$ \begin{array}{@{}rcl@{}} F(z) := - \frac{1}{n} \lim_{n\rightarrow\infty} p_{n}(z). \end{array} $$

(45)

Assuming this limit exists, then (45) implies p_n(z) ∼ exp(−nF(z)), i.e., the most probable values of the macrostate concentrate on the minima of the free energy. Moreover, given two macrostates $z_{1},z_{2}\in \mathbb {R}^{l}$, their relative stability can be characterized by the free energy difference: z₁ is more stable than z₂ if F(z₁) < F(z₂) and vice versa. In fact, the relative transition rates between z₁ and z₂ are exactly quantified by the free energy difference F(z₁) − F(z₂).

For non-equilibrium systems, however, the free energy (which comes from the invariant distribution) alone is insufficient to characterize relative stability. For example, the presence of non-trivial currents (say, cyclic transitions z₁ → z₂ → z₃ → z₁) may not alter the invariant distribution, but fundamentally affects transition dynamics. It turns out that if we turn to “path-space,” we may define an appropriate generalization of the free energy to non-equilibrium systems.

C.3 Free action

Fix a time horizon [0,τ] and consider the space of continuous functions $C^{0}\left (\left [0,\tau \right ],\mathbb {R}^{d\times n}\right )$. Each path x = {x (t) : t ∈ [0,τ]} of the Langevin process (41) is a member of this space. As a point of notation, we use boldface letters to denote such paths. For a fixed initial condition x (0) = x₀, the formal probability density of observing a path x is

$$ \begin{array}{@{}rcl@{}} \hat{\rho}_{n,\tau}\left[\mathbf{x}\right] \propto e^{-\tfrac{1}{\sigma} S_{n,\tau}\left[\mathbf{x}\right] }, \end{array} $$

(46)

where $S_{n,\tau }\left [\mathbf {x}\right ] =\frac {1}{4}{\int }_{0}^{\tau }\left \Vert \dot {x}\left (t\right )-f\left (x\left (t\right )\right )\right \Vert ^{2} dt$ is the action functional (Freidlin and Wentzell 2012). As seen from (46), the path probability density is formally an “equilibrium” distribution on path space (c.f. Eq. 43), where the role of the potential function is played by S_n,τ and the state space is now all possible paths.

Now, given macrostates z₁ and z₂, let us define the steady-state transition probability density from z₁ to z₂, which can be written as the path integral

$$ \begin{array}{@{}rcl@{}} \hat{p}_{n,\tau}\left( z_{1},z_{2}\right)&=&{\int}_{C^{0}}\delta\left( \phi_{n}\left[x\left( 0\right)\right] - z_{1}\right)\delta\left( \phi_{n}\left[x\left( \tau\right)\right] - z_{2}\right)\rho^{z_{1}}_{n}\\ &&\left[x\left( 0\right)\right] \hat{\rho}_{n,\tau}\left[\mathbf{x}\right] D\mathbf{x}, \end{array} $$

(47)

where ${\rho ^{z}_{n}}\left (\cdot \right )$ denotes the microstate invariant distribution ρ_n conditioned on ϕ_n (x) = z, i.e.,

$$ \begin{array}{@{}rcl@{}} {\rho^{z}_{n}}\left( x\right) = \frac{\rho_{n}\left( x\right)} {{\int}_{\mathbb{R}^{d\times n}}\delta\left[\phi_{n}\left( y\right)-z\right]\rho_{n}\left( y\right)dy}, \end{array} $$

(48)

for ϕ_n (x) = z and 0 otherwise.

Now, we define the free action in the thermodynamic limit

$$ \begin{array}{@{}rcl@{}} Q\left( z,w\right)=\lim_{n\rightarrow\infty}-n^{-1}\log\hat{p}_{n,\tau_{n}}\left( z,w\right), \end{array} $$

(49)

and we denote by $Q_{n,\tau }=-\log \hat {p}_{n,\tau }$ the free action for a finite system at finite times. τ_n is an appropriately chosen, increasing function of n. For this and most other applications, we may take τ_n ∝ n.

Physically, the free action measures the rate of decay of transition probabilities as the system size n grows. According to the discussion in Appendix B, this is important in characterizing the relative stability of macrostates. In particular, to compare the relative stability of states z,w, we may define the free action difference

$$ \begin{array}{@{}rcl@{}} {\Delta} Q(z_{1}, z_{2}) := Q(z_{2}, z_{1}) - Q(z_{1}, z_{2}). \end{array} $$

(50)

Then, ΔQ(z₁,z₂) > 0 implies the transition z₁ → z₂ is exponentially more likely than z₂ → z₁, and vice versa. Therefore, this gives us a means to identify phase transition points in non-equilibrium systems. Suppose z₁ and z₂ are two competing macrostate values representing two phases and the dynamics depend on some parameter w (rainfall in our case). Then, the phase transition point between z₁ and z₂ is exactly at the value of w for which ΔQ(z₁,z₂) = 0.

As a remark, it can be proved (Li and Weinan 2015) that for equilibrium systems with f = −∇V, we have ΔQ(z₁,z₂) = F(z₁) − F(z₂), i.e., the free action difference reduces to the free energy difference, and is hence a generalization of the free energy difference to non-equilibrium systems.

C.4 Numerical algorithm to compute the free action

One advantage of the free action is that it can be computed numerically even for very rare transitions. This is due to the path integral form of expression (51). Indeed, Eq. 51 has the form of a integral over a probability measure over path space, since we can write

$$ \begin{array}{@{}rcl@{}} \hat{p}_{n,\tau}\left( z_{1},z_{2}\right) = \left\langle \delta(\phi_{n}[x(\tau)] - z_{2}) \right\rangle_{n,\tau,z_{1}} \end{array} $$

(51)

where $\langle \cdot \rangle _{n,\tau ,z_{1}}$ denotes expectation over a distribution in the path space C⁰ with formal density $\mu _{n,\tau ,z_{1}}[\mathbf {x}]:=\delta (\phi _{n}[x(0)] - z_{1})\rho _{n}^{z_{1}}[x(0)] \hat {\rho }_{n,\tau }[\mathbf {x}] D\mathbf {x}$. Thus, we may estimate it by Markov chain Monte Carlo (MCMC) integration

$$ \begin{array}{@{}rcl@{}} \hat{p}_{n,\tau}\left( z_{1},z_{2}\right) \approx \frac{1}{N} \sum\limits_{i=1}^{N} \hat{\delta} (\phi_{n}[X^{(i)}(\tau)] - z_{2}) \end{array} $$

(52)

where X⁽ⁱ⁾, i = 1,…,N ≫ 1 is a Markov chain on the path space C⁰ with invariant distribution equal to $\mu _{n,\tau ,z_{1}}$ and $\hat {\delta }$ is an approximation to the delta function. The Markov chain can be constructed with the usual Metropolis-Hastings algorithm (Metropolis et al. 1953), but here we will require a modification that deals with high-dimensional problems (large n) using the Hamiltonian Monte Carlo method with pre-conditioning. Moreover, we use a form of thermodynamic integration similar to that in Ogata (1989) to further reduce the variance. With the value of $\hat {p}_{n,\tau }\left (z_{1},z_{2}\right )$ obtained for large n and τ, we may use formula (49) to compute the free action. The complete algorithmic detail is described in Li and Weinan (2015) and we omit repeating it entirely here.

We note that such MCMC algorithm to compute transition rates (and hence the free action) is fundamentally different from direct simulation of the dynamical (41). The transitions in the latter may be very rare. Yet, by performing Monte Carlo moves directly on path space, we can directly sample and obtain information on these rare transition paths. We note that similar ideas has been applied to the study of chemical reactions and other rare events (Dellago et al. 1998; Bolhuis et al. 2002).