Pearlite in Multicomponent Steels: Phenomenological Steady-State Modeling

Abstract

A steady-state model for austenite-to-pearlite transformation in multicomponent steel is presented, including Fe, C, and eight more elements. The model considers not only classic ingredients (formation of ferrite–cementite interface, volume diffusion, boundary diffusion, and optimization of lamellar spacing) but also finite austenite–pearlite interfacial mobility that resolves some previous difficulties. A non-Arrhenius behavior of interfacial mobility is revealed from growth rate and lamellar spacing data. A smooth and physical transition between orthopearlite and parapearlite is realized by optimizing the partitioning of substitutional alloying elements between ferrite and cementite to maximize growth rate or dissipation rate while keeping carbon at equilibrium. Solute drag effect is included, which accounts for the bay in growth rate curves. Grain boundary nucleation rate is modeled as a function of chemical composition, driving force, and temperature, with consideration of grain boundary equilibrium segregation. Overall transformation kinetics is obtained from growth rate and grain boundary nucleation rate, assuming pearlite colonies only nucleate on austenite grain boundaries. Further theoretical and experimental work are suggested for generalization and improvements.

1 Introduction

Pearlite is a common product of austenite decomposition in steels, typically consisting of alternating lamellae of ferrite and cementite. It is known as a product combining good strength and ductility obtained from relatively simple heat treatment of carbon or low-alloy steels. Pearlitic steels are widely used for steel wire and rail.[1] It is thus of great practical interest to accurately model the overall transformation kinetics of austenite decomposition to pearlite.

Quantitative experimental characterizations of pearlite date back to the 1930s.[2] Since then, there has been a compilation of information on the morphology, growth rate, lamellar spacing, partitioning of alloying elements, nucleation, and overall transformation kinetics of pearlite formation (see References 3,4,5, through 6 for example). The theory of pearlite formation has its stage set by Zener[7] and has been further developed by Hillert,[8,9,10] Cahn,[11,12] and others.[13,14,15,16,17,18] Industrially relevant calculation tools for pearlite include DICTRA as part of Thermo-Calc[19] based on the work of Jönsson,[20] and JMatPro based on the formulation by Kirkaldy et al.,[21] with various levels of predictability and user-friendliness.

In this work, we build a new model for pearlite formation, incorporating all major theoretical ingredients previously scattered in literature, with model parameters calibrated to best available experimental information. This work is built on the maturity of computational thermodynamics and diffusion kinetics in the framework of CALPHAD (CALculation of PHAse Diagram)[22] and has been incorporated in Thermo-Calc since Version 2019a.

Apart from the most common lamellar type of pearlite, there are also other types of pearlite, for example, pearlite with rod-shaped minority phase, divorced or degenerate pearlite with discontinuous lamellae or rods, or pearlite colony with non-spherical front, which we do not consider in this work. We also do not consider the effects of stress, deformation, or preexisting phase(s) on pearlite formation. In this work, we only deal with steady-state pearlite of which growth rate and nucleation rate are time-independent. It is future work to model pearlite with time-dependent growth rate (as known as divergent pearlite or partitioned pearlite) and time-dependent nucleation rate. The model is general for eutectoid/eutectic decomposition involving any three phases, but in this work we only present results of austenite (face-centered cubic or FCC, $\gamma$) decomposition to ferrite (body-centered cubic or BCC, $\alpha$) and cementite ($\theta$). Despite the limitations, our scope in this work should cover the most common circumstances of pearlite formation.

In this paper, we first present our model of the growth rate, nucleation rate, and overall transformation kinetics under the aforementioned assumptions. The model is then calibrated to available experimental data. Results of the Fe–C, Fe–C–Mn, and Fe–C–Cr systems, and two higher-order alloys, are presented to demonstrate the features of our model.

2 Modeling

2.1 Growth Rate

Growth rate $v,$ lamellar spacing S, and phase constitution of pearlite are determined by a balance of driving force and dissipation. Figure 1 is a schematic of the pearlite transformation front in our model. As the interface moves forward, driving force is consumed to create new ferrite–cementite interface area, to overcome the austenite–pearlite interfacial friction and solute drag force, and to drive partitioning of elements from ferrite to cementite (or the opposite) via volume diffusion in austenite and boundary diffusion. Next, we consider these contributions and finally combine them in a main equation of driving force–dissipation balance.

Fig. 1

Schematic of pearlite transformation front (thickness of boundary B exaggerated for clarity). See List of Symbols for definitions

2.1.1 Driving force

The total driving force for pearlite formation from austenite is the difference in Gibbs energy between the initial and final states:

$$ \Delta G_{m} = G_{m}^{\gamma } \left( {\left\{ {u_{i}^{0} } \right\}} \right) - \left[ {\left( {1 - f^{\theta } } \right)G_{m}^{\alpha } \left( {\left\{ {u_{i}^{\alpha } } \right\}} \right) + f^{\theta } G_{m}^{\theta } \left( {\left\{ {u_{i}^{\theta } } \right\}} \right)} \right] $$

(1)

It is defined as ${\Updelta}G_{m} > 0$ for pearlite formation. We express the composition using u fractions. These are defined from the ordinary mole fractions x_i as $u_{i} = x_{i} /\sum\nolimits_{k \in S} {x_{k} }.$ The summation in the denominator is performed over the substitutional elements (S) only. Let the concentrations of element $i$ at the interface in ferrite, cementite, and austenite be $u_{i}^{\alpha } ,u_{i}^{\theta },$ and $u_{i}^{\gamma },$ respectively. It is assumed $u_{i}^{\gamma } = u_{i}^{0},$ namely, the bulk austenite composition, in line with the steady-state assumption. The phase fractions, Gibbs energies, and compositions of ferrite and cementite can be determined assuming one of the following:

• (1) orthoequilibrium (OE, full equilibrium),

• (2) paraequilibrium (PE), where C reaches equilibrium under no partitioning of substitutional elements, and

• (3) constrained carbon equilibrium (CCE), where C reaches equilibrium under prescribed partitioning of substitutional elements (described in Section II–A–5).

2.1.2 Dissipation

The total driving force is assumed to be dissipated by four processes:

• (1) Formation of ferrite–cementite interface[7]

The free energy stored in the ferrite–cementite interface in one mole of pearlite is

$$ 2\sigma V_{m} /S $$

(2)

where $\sigma$ is the area-specific ferrite–cementite interfacial Gibbs energy, and $V_{m}$ is molar volume, which is assumed equal for austenite, ferrite, and cementite.

• (2) Pearlite–austenite interfacial friction

Pearlite forms by a reconstructive mechanism, which dissipates driving force. It is common to assume interfacial velocity is proportional to the part of the driving force ${\Updelta}G_{m}^{\rm I}$ dissipated by interfacial friction:

$$ v = M^{\rm I} \Delta G_{m}^{\rm I} $$

(3)

where the proportionality coefficient $M^{\rm I}$ is interfacial mobility. In this work, we consider the mobility of austenite–pearlite interface as a whole, without further dividing into austenite–ferrite and austenite–cementite interfaces separately.

• (3) Solute drag force on pearlite–austenite interface

Segregation or anti-segregation of an alloying element to a moving interface causes a drag force. The steady-state picture of solute drag on homophase and heterophase interfaces has been well established and utilized for modeling phase transformations with success.[23] Regardless of mathematical details, the basic features are in common: Segregation profile of alloying element is perturbed from its equilibrium profile in the low-velocity limit and is close to none in the high-velocity limit. Solute drag force is proportional to velocity in the low-velocity limit, reaches a maximum at an intermediate velocity, and becomes inverse proportional to velocity in the high-velocity limit. For multiple solute drag elements, their solute drag forces are assumed to be additive.

In this work, we find it sufficient to use a simple model for the solute drag effect on steady-state growth rate of pearlite. We adopt Cahn’s treatment[24] of solute drag, which turns out capable of reproducing the basic features mentioned above with a minimum of parameters. We use a symmetric wedge profile, within which boundary diffusivity (perpendicular to boundary) $D^{B \bot }$ is constant. Such a configuration allows an analytical expression of solute drag force (Appendix I). For each element that causes solute drag, model parameters are binding energy $E^{b}$ and the ratio of boundary diffusivity to full-width-half-maximum of the wedge, $D^{B \bot } /\delta.$

Atom probe tomographic results show that Mn segregates to the austenite–ferrite interface but not to austenite–cementite interface,[25] which supports an application of solute drag force only to the austenite–ferrite part of the interface. Therefore, binding energy values obtained here are expected to be comparable with those determined from modeling austenite–ferrite transformation in steels.

Based on the analysis above, we express the dissipative force due to solute drag of each element as

$$ \left( {1 - f^{\theta } } \right)\Delta G_{m}^{\rm SD} \left( {\frac{{E^{b} }}{RT}, \frac{{D^{B \bot } }}{v\delta }} \right) $$

(4)

The analytical form of ${\Updelta}G_{m}^{\rm SD}$ is given in Appendix I.

• (4) Diffusion of elements, within austenite and along pearlite–austenite interface

Now we consider partitioning of alloying elements within pearlite by diffusion. Diffusion can take place within austenite in front of the austenite–pearlite interface and/or along the austenite–pearlite interface.

There have been models with different levels of sophistication describing the shape of pearlite–austenite interface based on capillarity and its effect in thermodynamics.[15,16,20,26] However, interfacial mobility is infinite in most of the models. Introducing finite interfacial mobility makes capillarity consideration difficult because force balance at the austenite–ferrite–cementite junction is complicated. In addition, it is revealed in microstructural observations[6,27] that the interface is mostly flat except in a limited neighborhood of the triple-phase junction, which casts doubt on the necessity of introducing capillarity with high sophistication.

Here, we use a simple but effective model handling volume and boundary diffusion. Local equilibrium is not assumed at the interface.

A detailed derivation is given in Appendix II. Here, we only show the final result of the total dissipative force due to diffusion, within austenite and along austenite–pearlite interface in parallel:

$$ \frac{{vS\left( {f^{\theta } } \right)^{2} }}{2}\frac{{\left( {u_{i}^{0} - u_{i}^{\theta } } \right)^{2} }}{{u_{i}^{0} \left[ {M_{i}^{\gamma } + \frac{{2\left( {kM^{B\parallel } \delta } \right)_{i} }}{S}} \right]}} $$

(5)

We can define a ratio $r_{i} = 2\left( {kM^{B\parallel } \delta } \right)_{i} /M_{i}^{\gamma } S$ for relative weight of boundary diffusion and volume diffusion of element $i.$ Limiting cases of volume diffusion only and boundary diffusion only can be reproduced by setting $kM^{B\parallel } \delta = 0$ ($r = 0$) and $M_{i}^{\gamma } = 0$ ($r \to + \infty$), respectively.

2.1.3 The main equation

The main driving force–dissipation balance equation is then

$$ \Delta G_{m} = \frac{{2\sigma V_{m} }}{S} + \frac{v}{{M^{\rm I} }} + \left( {1 - f^{\theta } } \right)\mathop \sum \limits_{j = 1}^{m} \Delta G_{m,j}^{\rm SD} \left( {v, \left\{ {\frac{{E^{b} }}{RT}, \frac{{D^{B \bot } }}{\delta }} \right\}_{j} } \right) + \frac{{vS\left( {f^{\theta } } \right)^{2} }}{2}\mathop \sum \limits_{i = 1}^{n} \frac{{\left( {u_{i}^{0} - u_{i}^{\theta } } \right)^{2} }}{{u_{i}^{0} \left[ {M_{i}^{\gamma } + \frac{{2\left( {kM^{B\parallel } \delta } \right)_{i} }}{S}} \right]}} $$

(6)

Assuming dissipation from each element is additive, the total solute drag force sums over $m$ solute drag elements, and the total dissipative force from diffusion sums over all $n$ elements (including Fe, if lattice-fixed frame is used). If we neglect the thermodynamic interactions in boundary diffusion, we can link atomic mobility in boundary $M^{B\parallel }$ to atomic diffusivity in boundary $D^{B\parallel }$ (not to be confused with $D^{B \bot }$ used for solute drag effect in Eq. [4]). Both the segregation ratio $k$ and boundary diffusivity $D^{B\parallel }$ are expected to follow the Arrhenius equation. Therefore,

$$ \left( {kM^{B\parallel } \delta } \right)RT = \left( {kD^{B\parallel } \delta } \right) = \left( {kD^{B\parallel } \delta } \right)_{0} \exp \left( { - \frac{{Q^{\rm B} }}{RT}} \right) $$

(7)

The activation energy $Q^{\rm B}$ is the activation energy for boundary diffusivity subtracted by the binding energy to austenite–pearlite interface (Section III–A–1).

Equation [6] is the main equation for calculating $v,$ if $S$ and compositions in austenite, ferrite, and cementite are known. Without the solute drag term, $v$ is directly solvable. Otherwise, the equation is implicit to $v$ and it has to be solved iteratively.

It is also useful to define the critical spacing S_c by

$$ \Delta G_{m} = \frac{{2\sigma V_{m} }}{{S_{\rm c} }} $$

(8)

This means all the driving force is used to create new ferrite–cementite interface, leaving no driving force available for the other processes, hence $v = 0.$

2.1.4 Maximizing growth rate or dissipation rate

Given phase compositions and hence driving force, we have established the $v\left( S \right)$ relationship. A unique $S$ has to be determined by introducing some criterion. In this work, we consider maximizing growth rate $v,$[7] or maximizing rate of dissipation (except the Gibbs energy stored in ferrite–cementite interface) $v\left( {{\Updelta}G_{m} - 2\sigma V_{m} /S} \right),$ with respect to $S.$ Other options include maximizing total driving force ${\Updelta}G_{m}$[11] or total entropy production rate $v{\Updelta}G_{m} /T.$[14]

The result of maximizing growth rate conceptually corresponds to the maximal growth rate measured from maximal nodule radius (MNR) in metallography of isothermally heat-treated alloys. It is also acceptable to use this criterion for forced velocity growth of pearlite because it gives similar results to isothermal heat treatment.[28] Maximizing dissipation gives a smaller growth rate and a larger lamellar spacing, which may better represent the average values among all pearlite colonies. The criteria of maximizing certain quantities are not fully justified and merely provide convenient ways to give unique values of lamellar spacing.

In this work, we use the criterion of maximizing growth rate if not specified otherwise.

2.1.5 Constrained carbon equilibrium (CCE) and optimal pearlite

As mentioned, common ways to determine phase compositions and driving force include assuming orthoequilibrium or paraequilibrium between ferrite and cementite. However, electron probe measurements of the partition coefficients of substitutional alloying elements $K_{i} = u_{i}^{\theta } /u_{i}^{\alpha }$ suggest a continuous transition from near orthoequilibrium to paraequilibrium as temperature is lowered (See Ridley[29] and references therein. Note that experimentally measured partition coefficients are usually expressed in weight fractions $K_{i}^{w} = w_{i}^{\theta } /w_{i}^{\alpha }$). The continuous transition shows that assuming either orthoequilibrium or paraequilibrium is too simplistic.

In this work, we move beyond the limiting assumptions of either orthoequilibrium or paraequilibrium, by applying the criterion in Section II–A–4 to determine both S and the partition coefficients of substitutional alloying elements. Meanwhile, we assume the fast diffusing element C reaches equilibrium between ferrite and cementite under the prescribed partition coefficients $\left\{ {K_{i} } \right\} \left( {i \ne {\text{C}}, {\text{Fe}}} \right),$ which is a type of constrained carbon equilibrium (CCE). Numerically, given $\left\{ {K_{i} } \right\} \left( {i \ne {\text{C}}, {\text{Fe}}} \right),$ CCE is found by minimizing Gibbs energy of the ferrite–cementite system while keeping mass balance:

$$ \begin{aligned} {\text{Given }}\left\{ {K_{i} } \right\}, i \ne {\text{C}},{\text{Fe}} \hfill \\ {\text{Minimize }}G_{m}^{\alpha \theta } \left( {f^{\theta } } \right) = \left( {1 - f^{\theta } } \right)G_{m}^{\alpha } \left( {\left\{ {u_{i}^{\alpha } } \right\}} \right) + f^{\theta } G_{m}^{\theta } \left( {\left\{ {u_{i}^{\theta } } \right\}} \right), i \ne {\text{Fe}} \hfill \\ {\text{With }}u_{i}^{\alpha } = \frac{{u_{i}^{0} }}{{1 + \left( {K_{i} - 1} \right)f^{\theta } }}, u_{i}^{\theta } = K_{i} u_{i}^{\alpha } , i \ne {\text{C}},{\text{Fe}} \hfill \\ u_{\rm C}^{\alpha } = \frac{{u_{\rm C}^{0} - f^{\theta } u_{\rm C}^{\theta } }}{{1 - f^{\theta } }}, u_{\rm C}^{\theta } = \frac{1}{3} \hfill \\ \end{aligned} $$

(9)

Here, we assume the stoichiometry of cementite is (Fe, X)₃(C)₁ in the absence of B and N, and vacancies which enter the same sublattice as C. The stoichiometry makes ferrite–cementite system Gibbs energy $G_{m}^{\alpha \theta }$ a univariate function of molar fraction of cementite $f^{\theta }.$ If B, N, and vacancies are also allowed together with C, a more general algorithm must be used for finding constrained equilibrium.

The CCE solution includes cementite fraction $f^{\theta },$ compositions of ferrite and cementite $\left\{ {u_{i}^{\alpha } } \right\}$ and $\left\{ {u_{i}^{\theta } } \right\},$ and hence driving force ${\Updelta}G_{m}$ from Eq. [1]. Then, growth rate or dissipation is readily solvable from Eq. [6] with a given $S.$ In an outer loop, a unique vector $\left[ {S, K_{1} , K_{2} , \ldots , K_{n - 2} } \right]$ is obtained as the solution of maximizing growth rate or dissipation rate (Section II–A–4). We name the pearlite mode “optimal pearlite.”

2.2 Nucleation Rate

2.2.1 Grain boundary (GB) nucleation rate

Metallographic evidence[3,12,30] shows that pearlite does not nucleate homogeneously in bulk austenite, but heterogeneously on austenite grain boundaries (GBs) and their edges and corners, or sample surface. Under most common circumstances, it is quite safe to only consider GB nucleation,[3] except probably for very low driving force and nucleation rate. Therefore, Cahn’s analysis[31] is better than the standard equation from Johnson, Mehl, Avrami, and Kolmogorov (JMAK) for homogeneous bulk nucleation.[12] Following Cahn’s analysis, we calculate phase fraction as a function of time, given a constant growth rate (from Section II–A) and GB nucleation rate.

GB nucleation rate has been derived from number density of pearlite colonies from either metallography[12] or indirect measurement.[32] Existing evidence all supports a non-steady-state GB nucleation process, with a nucleation rate increasing with time throughout the entire transformation. However, published quantitative research on nucleation rate of pearlite is too limited to allow modeling in a practically wide range in composition and temperature. An additional difficulty is a lack of nucleation theory for eutectoid/eutectic transformation product. The process of GB nucleation of pearlite has been conceptualized,[5,33] but it remains unclear how these concepts can help build quantitative theoretical models for pearlite nucleation rate.

Alternatively, nucleation rate as a function of time can also be induced from high-quality curve of fraction of pearlite over time, if growth is steady-state and the growth rate is known.[12] Unfortunately, the pearlite fraction is not systematically measured either. For industrial steels, most commonly documented are simply TTT (temperature–time–transformation) diagrams including times of “start” and “finish,” occasionally also a few intermediate phase fractions. Definitions of “start” and “finish” can also be ambiguous or mutually incompatible.

Because of such shortages of theoretical advances and experimental information about pearlite nucleation in a general steel, in this work we limit ourselves to using time-independent nucleation rate, which is determined by fitting to experimental start and finish times. We assume “start” corresponds to 2 pct transformation, and “finish” to 98 pct transformation, if not specified otherwise. We use the following equation for temperature dependence of GB nucleation rate:

$$ J^{0} \left( T \right) = J^{00} \left( {\frac{{\Delta G_{m} }}{{RT_{r} }}} \right)^{n} \exp \left( { - \frac{{Q^{N} }}{RT}} \right) $$

(10)

where J⁰⁰ is a prefactor, T_r = 100 K is a reference temperature simply to normalize the driving force, n is a positive exponent, and $Q^{N}$ is an activation energy to ensure that low-temperature nucleation rate is diffusion-limited. The expression for $J^{0} \left( T \right)$ is then a C-curve with temperature. Then we model J⁰⁰ and n as functions of system composition.

2.2.2 Effect of equilibrium segregation at austenite GB on pearlite nucleation

In Section II, we have considered steady-state solute drag effect on pearlite growth rate. The effect is to create a bay on the growth rate–temperature curve. However, for some systems, the bay in growth rate is not sufficient to account for the bay in the TTT diagram: Another bay in nucleation rate curve should be added to Eq. [10]. This is justified by segregation of alloying elements to prior austenite GBs, assuming some element prohibits pearlite nucleation upon its segregation to austenite GB. By the onset of pearlite nucleation, the amount of segregation at high temperature is limited by normalized GB segregation energy E^GB/RT, while at low temperature by diffusional kinetics. At some intermediate temperature, the amount of segregation within a certain time reaches a maximum. Such a behavior has been modeled with success for P in steel using McLean-type isotherm.[34] Therefore, considering the thermodynamics and diffusional kinetics of GB segregation is expected to create a bay in nucleation rate–temperature curve, if the GB segregant suppresses pearlite nucleation.

However, to keep consistent within the time-independent framework, we are focused on equilibrium segregation only. This will give the upper half of a bay without returning to the case of negligible segregation at low temperature. This is acceptable for Cr, as is shown in Section III–D, but not for all elements.

Based on the arguments above, the parameters J⁰⁰ and n in Eq. [10] should depend on GB composition instead of nominal composition. Assuming dilute solution thermodynamics, equilibrium GB composition is calculated by:

$$ u_{i}^{GB} = u_{i}^{0} \exp \left( {\frac{{E_{i}^{GB} }}{RT}} \right) $$

(11)

2.3 Overall Transformation Kinetics

We adopt Cahn’s analysis[31] and restate key results here. In this work, both growth rate and grain boundary nucleation rate are time-independent; therefore, the overall transformation kinetics, namely, pearlite fraction X over time t, is given by

$$ \begin{aligned} X\left( t \right) & = 1 - \exp \left[ { - b_{\rm s}^{ - 1/3} f_{\rm s} \left( {a_{\rm s} } \right)} \right] \\ a_{\rm s} & = \left( {J^{0} v^{2} } \right)^{1/3} t \\ b_{\rm s} & = J^{0} /\left( {8S_{G}^{3} v} \right) \\ f_{\rm s} \left( {a_{\rm s} } \right) & = a_{\rm s} \mathop \smallint \limits_{0}^{1} dx\left\{ {1 - \exp \left[ { - \pi a_{\rm s}^{3} \left( {\frac{{1 - x^{3} }}{3} - x^{2} \left( {1 - x} \right)} \right)} \right]} \right\} \\ \end{aligned} $$

(12)

where $x = y/vt,$y being distance from GB, and $S_{G}$ is GB area per unit sample volume. Assuming grains are equally large space-filling tetrakaidecahedra with distance $D_{G}$ between their square faces, D_G can be regarded as grain size and $S_{G} = 3.35D_{G}^{ - 1}.$ Grain boundary coverage is the area fraction of transformation product at zero distance from GB, given by

$$ Y_{0} \left( t \right) = 1 - \exp \left[ { - Y_{e} \left( {t,x = 0} \right)} \right] = 1 - \exp \left( { - \frac{1}{3}\pi J^{0} v^{2} t^{3} } \right) $$

(13)

The calculation can be summarized in Figure 2.

Fig. 2

Calculation flow diagram of the present model

3 Results

All the calculations are done using Thermo-Calc Software TCFE9 Steels/Fe-alloys database and MOBFE4 Steels/Fe-alloys mobility database. Experimental data and back-calculations from them are plotted in scattered symbols, and model calculations in continuous curves.

3.1 Growth of Fe–C Pearlite

Experimental measurements of growth rate and lamellar spacing are available. We take both the maximal nodule radius (MNR) and minimal lamellar spacing from isothermal treatments and unidirectional growth (forced velocity) experiments.

For the Fe–C system, there are only three parameters to determine: ferrite–cementite interfacial Gibbs energy $\sigma,$ the product $\left( {kM^{B\parallel } \delta } \right)$ for C, and interfacial mobility $M^{\rm I}.$ Boundary mobility or diffusivity is determined by calibrating our model to experimental data on pearlite. Except for Fe, $\left( {kM^{B\parallel } \delta } \right)$ is not taken from measurements of diffusion along grain boundaries in ferrite or austenite[35] because of a difference in physical meaning (stationary vs moving boundary, homophase vs heterophase boundary) and large scatter among literature values.

3.1.1 Difficulties when assuming infinite interfacial mobility

We first examine the assumption of infinite interfacial mobility, which is accepted in most of existing analyses. In this case, the two remaining model parameters $\left[ {\sigma , \left( {kD^{B\parallel } \delta } \right)_{\rm C} } \right]$ can be uniquely determined by a pair of experimental data $\left( {v_{max} ,S_{min} } \right)$ at each temperature, available from References 28, 36, and 37.

In Figure 3, we overlay the results from our simple model and the treatments of Sundquist[15] and Hashiguchi and Kirkaldy[16] which are more sophisticated. Both consider detailed geometry of the transformation front based on capillarity, local equilibrium at interface, and volume diffusion field in bulk austenite.[16] Sundquist uses a fixed σ = 0.7 J m⁻², but his $\left( {kD^{B\parallel } \delta } \right)_{\rm C}$ values are quite close to our back-calculations. Hashiguchi and Kirkaldy assume maximized entropy production rate, which presumably causes the slight differences in $\sigma$ and $\left( {kD^{B\parallel } \delta } \right)_{\rm C}$ from our back-calculations. Despite the minor differences, our simplified model is almost equally capable of describing pearlite growth quantitatively in comparison with the more sophisticated treatments.

Fig. 3

Results assuming infinite interfacial mobility: (a) Ferrite-cementite interfacial Gibbs energy $\sigma$ and (b) $\left( {kD^{B\parallel } \delta } \right)$ of carbon, back-calculated in this work, by Hashiguchi and Kirkaldy,[16] and Sundquist.[15] Also shown are experimental measurements[38,39] of $\sigma.$ Experimental data used for back-calculation: (c) maximal growth rate and (d) minimal lamellar spacing taken from Refs. [28], [36], and [37]

In literature, the results have been criticized for two arguments, which we examine below:

• (1) The activation energy of $\left( {kD^{B\parallel } \delta } \right)_{\rm C}$ is too high

The activation energy of $\left( {kD^{B\parallel } \delta } \right)_{\rm C}$ is about 191 kJ mol⁻¹[15] or 170 kJ mol⁻¹.[16] There have been arguments that this is too high for diffusivity along a boundary which acts as a shortcut. Some values close to that of volume diffusion of C in ferrite, about 90 kJ mol⁻¹, are preferred. The apparently too high activation energy is attributed to impurity segregation.[15,40]$Q_{\rm C}^{\rm B}$ is the activation energy for boundary diffusivity $D^{B\parallel }$ subtracted by the binding energy of C to austenite–pearlite interface. Hashiguchi and Kirkaldy made an attempt to separate the two parts, estimating the binding energy to be several tens of kJ mol⁻¹,[16] which means the activation energy of $D^{B\parallel }$ is even higher than that of $\left( {kD^{B\parallel } \delta } \right)_{\rm C}$

However, recent atomistic simulation[41] shows that C diffusion along GB in pure Fe does not necessarily exhibit a lower activation energy than volume diffusion, the difference depending significantly on grain boundary structure.

In light of these arguments, the resultant activation energy is acceptable.

• (2) Ferrite–cementite interfacial Gibbs energy $\sigma$ and interfacial entropy $\sigma_{\rm S} = - {\text{d}}\sigma /{\text{d}}T$ are too high

The magnitude of $\sigma > 1$ J m⁻² is comparable to some surface energy[42] and is apparently too high for the ferrite–cementite interface, compared to the experimental measurements.[38,39] The interfacial entropy $\sigma_{\rm S} = - {\text{d}}\sigma /{\text{d}}T$ is up to 0.008 J m⁻² K⁻¹, also too high to accept for a solid–solid interface. Sundquist[15] adopted a value of $\sigma = 0.7$J m⁻² but the calculated lamellar spacing which maximizes growth rate was smaller than experimental measured values by nearly one order of magnitude.

As discussed in the two points above, we can accept an activation energy of $\left( {kD^{B\parallel } \delta } \right)_{\rm C}$ higher than that of bulk diffusion, but cannot accept the too high interfacial Gibbs energy to be physical. Therefore, it is unrealistic to assume an infinite interfacial mobility for pearlite formation in steels.

3.1.2 Finite interfacial mobility

The difficulty from interfacial properties described in Section III–A–1 can be resolved by introducing a finite interfacial mobility, which originates from the reconstructive nature of pearlite formation. Finite interfacial mobility has been considered in modeling cellular reactions,[9,11] but much less appreciated in modeling pearlite in steels. The work by Togashi and Nishizawa[40] includes arguably the best assessment of austenite–pearlite interfacial mobility by far.

Now we have three model parameters $\sigma,$$M^{\rm I},$ and $\left( {kD^{B\parallel } \delta } \right)_{\rm C}$ which cannot be uniquely determined from two measurements $\left( {v_{max} ,S_{min} } \right).$ We then have the freedom to choose interfacial Gibbs energy and make it constant over temperature, because this is the physical quantity that is expected to vary least within the temperature range of pearlite formation. Then, a pair of $\left[ {M^{\rm I} , \left( {kD^{B\parallel } \delta } \right)_{\rm C} } \right]$ can be uniquely determined from $\left( {v_{max} , S_{min} } \right),$ as shown in Figure 4. In this work, we adopt $\sigma$ = 0.5 J m⁻² for Fe–C pearlite. For other values between 0.2 and 1.0 J m⁻², the results are slightly offset and rotated in an Arrhenius plot, while the qualitative picture remains the same.

Fig. 4

Results assuming finite interfacial mobility and $\sigma = 0.5$ J m⁻²: (a) interfacial mobility and (b) $\left( {kD^{B\parallel } \delta } \right)$ of carbon determined from the same experimental dataset as in Fig. 3.[28,36,37] Data points in solid symbols are utilized for fitting

As expected, $\left( {kD^{B\parallel } \delta } \right)_{\rm C}$ follows the Arrhenius equation. We assume $\left( {kD^{B\parallel } \delta } \right)_{\rm C}$ and $M^{\rm I}$ are independent of overall C concentration, as suggested by the results from three different Fe–C alloys.[28,36,37] Using the data from Pearson and Verhoeven[28] for an upper intercept and slope and the data from Cheetham and Ridley[37] for a lower intercept, we adopt an average intercept and write

$$ \left( {kD^{B\parallel } \delta } \right)_{\rm C} = 1.774 \times 10^{ - 9} \exp \left( { - \frac{{1.737 \times 10^{5}\, {\text{J}}\,{\text{mol}}^{ - 1} }}{RT}} \right){\text{m}}^{3}\,{\text{s}}^{ - 1} $$

(14)

3.1.3 Temperature dependence of interfacial mobility

After $\left( {kD^{B\parallel } \delta } \right)_{\rm C}$ is determined in Eq. [14], we can now make use of the datapoints with only MNR growth rate measured,[3,30,43,44] and obtain $M^{\rm I}$ below the nose temperature. The results, which now cover a much larger temperature range, are shown in Figure 5 together with austenite–ferrite interfacial mobility for comparison. It is clear that the non-Arrhenius behavior indicated already in Figure 4(a) is so pronounced that there is even a maximum at $10^{3} /T \cong 1.1{\text{K}}^{ - 1}.$

Fig. 5

Interfacial mobility determined from either growth rate or lamellar spacing data[3,28,30,36,37,43,44] using $\sigma = 0.5$ J m⁻² and $\left( {kD^{B\parallel } \delta } \right)$ of carbon from Eq. [14], in filled symbols. The continuous curve is fitted using Eq. [15]. Also overlaid are austenite-massive ferrite interfacial mobility (in unfilled symbols) data from Figs. 1 and 3 of Hillert and Höglund[45] (and references therein) and Zhu et al.[46]

There is not a clear dependence of $M^{\rm I}$ on overall C concentration and thus on cementite fraction. Therefore, further analysis of $M^{\rm I}$ based on a mixture of austenite–ferrite and austenite–cementite interfaces is difficult. On the temperature dependence, the $M^{\rm I}$ of Fe–C pearlite is connected to the data of massive ferrite at 1000 K and undergoes a smooth transition to a higher Arrhenius line as temperature decreases. Such a non-Arrhenius temperature dependence of $M^{\rm I}$ is also found by Togashi and Nishizawa.[40]

In this work, instead of describing $M^{\rm I}$ based on physical mechanisms, we simply use a mathematical equation to fit $M^{\rm I}$ as a function of temperature (Eq. [15]).

$$ \begin{aligned} \ln M^{\rm I} & = \left( {1 - f^{\rm I} } \right)\ln M_{\rm low}^{\rm I} + f^{\rm I} \ln M_{\rm high}^{\rm I} \\ \ln M_{\rm low}^{\rm I} & = \ln M_{\rm low}^{I0} - \frac{{Q^{\rm I} }}{RT} \\ \ln M_{\rm high}^{\rm I} & = \ln M_{\rm high}^{I0} - \frac{{Q^{\rm I} }}{RT} \\ f^{\rm I} & = 1 - \exp \left( { - \frac{{T_{0}^{p} - T}}{{T_{\lambda } }}} \right) \\ \end{aligned} $$

(15)

Equation [15] represents a transition from one Arrhenius equation to another. The transition starts at the temperature $T_{0}^{p}$ at which the driving force from austenite to pearlite with the same composition is zero.[12] $T_{0}^{p}$ is different from the commonly defined A₁ temperature except for eutectoid Fe–C alloy (0.77 wt pct C, 1000 K). The value suggested by Zhu et al.,[46] $Q^{\rm I} = 1.45 \times 10^{5}$ J mol⁻¹, is accepted. The other fitting parameters are $\ln M_{\rm low}^{I0},$$\ln M_{\rm high}^{I0},$ and $T_{\lambda }.$ Fitting to the results for Fe–C pearlite gives $M_{\rm low}^{I0} = 0.3965 {\text{m mol J}}^{ - 1} {\text{s}}^{ - 1} , M_{\rm high}^{I0} = 123.5 {\text{m mol J}}^{ - 1} {\text{s}}^{ - 1} , T_{\lambda } = 56.68{\text{K}}.$

We emphasize that Eq. [15] does not have any clear physical meaning and is merely a method of representing the interfacial mobility.

3.1.4 Results of Fe–C pearlite growth

Now we have determined all the model parameters for growth of Fe–C pearlite. Growth rate and lamellar spacing calculated using the model parameters are compared to experimental measurements in Figure 6.

Fig. 6

(a) Growth rate and (b) reciprocal lamellar spacing of Fe–C pearlite, calculation (0.77 wt pct C) vs experimental[3,28,30,36,37,43,44,47,48] (average lamellar spacing from Ref. [44] and minimal from the others)

In Figure 7(a), we plot the driving force for pearlite formation and how it is dissipated by formation of ferrite–cementite interface, interfacial friction, and C diffusion (boundary diffusion and volume diffusion in parallel). Historically, there has been significant work attempting to identify one single controlling mechanism from scaling laws.[48,49] The current model makes it unnecessary because how driving force is dissipated results from a proper calibration of the model. Even for the simplest case Fe–C, pearlite formation is under mixed control. In Figure 7(b), we plot the ratio $r,$ from which we can see boundary diffusion of C is more important than volume diffusion by a factor of about 20. Although Fe does not partition in Fe–C pearlite, the same ratio can still be defined for Fe, taking $\left( {kD^{B\parallel } \delta } \right)_{\text{Fe}} = 9.03 \times 10^{ - 13} \exp \left( { - 180500\,{\text{J}}\,{\text{mol}}^{-1}/RT} \right)$ m³ s⁻¹.[35] The ratio $r_{\text{Fe}}$ is several orders of magnitude higher than that of C, showing a predominance of boundary diffusion to volume diffusion. This is also the case for substitutional alloying elements.

Fig. 7

(a) Driving force and dissipation, Fe–C pearlite, (b) ratio r as a measure of relative weight of boundary diffusion and volume diffusion

In Figure 8, we compare growth rate–lamellar spacing curves with infinite and finite interfacial mobility of Fe–0.77C (wt pct, same below unless specified otherwise) at T = 800 K, other parameters being the same. The curve with infinite interfacial mobility starts from zero at $S/S_{\rm c} = 1,$ reaches its maximum, and decays to zero as $S/S_{\rm c} \to + \infty.$ The value of $S/S_{\rm c}$ which maximizes growth rate (1.502) lies between the limiting cases of boundary diffusion control (1.5) and volume diffusion control (2.0), while being much closer to the former. Introducing a finite interfacial mobility moves the maximum of the curve to a larger $S/S_{\rm c} = 4.65$ and lower growth rate. This can account for Sundquist’s note[15] that the observed lamellar spacing is several times larger than the calculated value assuming infinite interfacial mobility (which cannot exceed $2S_{\rm c}$) if a reasonable interfacial Gibbs energy is adopted. In addition, finite interfacial mobility makes the maximum flatter. If the shape of $v\left( S \right)$ curve near the maximum has some implication on the distribution of $S$ and $v,$ finite interfacial mobility possibly leads to a wider distribution in lamellar spacing but a narrower one in growth rate below its maximum.

Fig. 8

Growth rate as a function of lamellar spacing, with infinite or finite interfacial mobility, Fe–0.77C at T = 800 K. Curve’s maxima marked with “+”

3.2 Growth of Fe–C–Mn Pearlite: Orthopearlite, Parapearlite, and Optimal Pearlite

We have compiled experimental data of ternary alloys Fe–C–X (X = Mn,[30,50,51,52] Cr,[50,52,53,54,55] Mo,[40,52,56,57] W,[58] Si,[59] Ni,[36,60] Co,[49,61,62]) and calibrated the model with critical assessment. Model parameters determined include the Arrhenius equations for $\left( {kD^{B\parallel } \delta } \right)_{X},$ and effects of X on $\sigma,$$M^{\rm I},$ and $\left( {kD^{B\parallel } \delta } \right)_{\rm C}.$ We assume Al has the same model parameters as Si. Growth rate curves for X = Cr and Mo have obvious bays, and accordingly $E^{b}$ and $D^{B \bot } /\delta$ of Cr and Mo are determined by fitting to growth rate and lamellar spacing.

In this paper, we use Fe–0.69C–1.80Mn to demonstrate optimal pearlite compared to orthopearlite and parapearlite, and use Fe–0.6C–1.78Cr to demonstrate the effect of solute drag. We use the following parameters in Table I for the two alloys.

Table I Model Parameters (all in SI Units as Specified in List of Symbols)

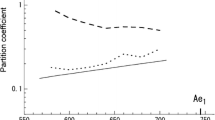
We calculate the ferrite–cementite CCE at 900 K in Fe–0.69C–1.80Mn using Eq. [9]. From Figure 9, we can see CCE reduces to paraequilibrium if $K\left( {\text{Mn}} \right) = 1$ and orthoequilibrium if $K\left( {\text{Mn}} \right)$ is chosen to minimize the ferrite–cementite system Gibbs energy (hence driving force maximized).

Fig. 9

Orthoequilibrium (OE), paraequilibrium (PE), and CCE between ferrite and cementite in Fe–0.69C–1.80Mn at T = 900 K, showing (a) C activity $a\left( C \right)$ (reference: graphite), cementite volume fraction $f^{\theta },$ and (b) austenite-to-pearlite driving force $\Delta G_{m}$ as functions of partition coefficient of Mn between cementite and ferrite ${\text{K}}\left( {\text{Mn}} \right)$

Under CCE, growth rate is a function of lamellar spacing and partition coefficient of Mn. The two-dimensional function is shown in Figure 10. The locus $\partial v/\partial S = 0$ gives the $S$ which maximizes $v$ at a given $K,$ and para- and orthopearlite are two points on the locus. The other locus $\partial v/\partial K = 0$ represents the $K$ at which $v$ is maximized at a given $S.$ The intersection of the two loci represents the globally maximized $v,$ namely, the solution of optimal pearlite.

Fig. 10

Growth rate as a function of partition coefficient of Mn and lamellar spacing. Fe–0.69C–1.80Mn at T = 900 K

Growth rate, lamellar spacing, and partition coefficient of Mn of ortho-, para-, and optimal pearlite are plotted in Figure 11. It can be seen that optimal pearlite approaches orthopearlite at high temperature and parapearlite at low temperature, with a smooth transition in between where it grows faster than both the other two modes.

Fig. 11

Growth rate, lamellar spacing, and partition coefficient (in weight fraction) of Mn of (a) ortho-, (b) para-, and (c) optimal pearlite in Fe–0.69C–1.80Mn. Experimental measurement from Ref. [51]

The optimal partition coefficient follows the same trend as experimental measurements, but is several times larger. Experimentally, the techniques used in Razik et al.[51] have been critically examined by Chance and Ridley,[52,55] who concluded the partition coefficients from Razik et al. are too low. Computationally, we point out that partition coefficient is dependent on lamellar spacing. For a suboptimal lamellar spacing, the most probable partition coefficient can be given by $\partial v/\partial K = 0.$ It can be seen from Figure 10 that a lamellar spacing larger than the optimum corresponds to a smaller partition coefficient. It is also somewhat intuitive that partitioning should be weakened if it takes place over a longer transport distance (lamellar spacing). Experimentally measured partition coefficient does not usually correspond to minimal lamellar spacing—in some cases, small lamellar spacing is deliberately avoided because the size of electron probe cannot fit in for accurate composition measurement.[51] This can explain why measured partition coefficients can be very different (for example, between Razik et al.[51] and Chance[52] for 1Mn steel), and why calculated optimal partition coefficient is higher than measured.

In Figure 12, we plot the total driving force and its dissipation by forming ferrite–cementite interface, interfacial motion, diffusion by C, Mn, and Fe, for ortho-, para-, and optimal pearlite. Of interest is the element which causes the largest dissipation by diffusion: Mn in orthopearlite, C in parapearlite (the only partitioning element), and a transition from Mn to C as temperature is lowered for optimal pearlite.

Fig. 12

Driving force and dissipation of (a) ortho-, (b) para-, and (c) optimal pearlite in Fe–0.69C–1.80Mn

3.3 Growth of Fe–0.6C–1.78Cr Pearlite: Solute Drag Effect

Solute drag effect creates a bay in growth rate and reciprocal lamellar spacing towards their lower sides, and a step in partition coefficient towards its higher side, approximately between 880 K and 950 K for Fe–0.6C–1.78Cr (Figure 13). The step of partition coefficient is seen from experimental measurements of another alloy with slightly lower Cr concentration. From Figure 14 which shows the driving force and dissipation, solute drag consumes up to a half of the total driving force. The alloy undergoes a transition from orthopearlite to parapearlite also, but solute drag retards the transition when it is operative, in favor of orthopearlite.

Fig. 13

(a) Growth rate, (b) lamellar spacing, and (c) partition coefficient (in weight fraction) of Cr of optimal pearlite in Fe–0.6C–1.78Cr, with and without solute drag. Also shown is $v_{0}$ where solute drag force is maximized with respect to $v.$ Experimental measurements from Sharma et al.[54] and Chance and Ridley (Fe–0.82C–1.42Cr).[52,55]

Fig. 14

Driving force and dissipation of optimal pearlite in Fe–0.6C–1.78Cr, (a) with and (b) without solute drag

Figure 15 shows a typical shape of growth rate $v$ as a function of partition coefficient $K$ of Cr and lamellar spacing $S,$ with and without solute drag effect. Solute drag moves the optimum towards higher $K\left( {\text{Cr}} \right)$ and larger $S,$ and flattens the top of $v\left( {K,S} \right).$ If the behavior near the optimum has some implication to the distribution of growth rate and lamellar spacing, strong solute drag effect implies a large scatter in both $K$ and $S.$ This is somewhat in accordance with the reported large scatter in lamellar spacing in Fe–C–Mo pearlite[63] where solute drag also exists.

Fig. 15

Growth rate as a function of partition coefficient of Cr and lamellar spacing, (a) with and (b) without solute drag

3.4 Nucleation Rate and Overall Transformation Kinetics

Knowing the steady-state growth rate, the nucleation rate is determined by fitting to overall transformation kinetics. The parameters for the Fe–C and Fe–C–Cr systems are presented in Table II. Figure 16 shows the nucleation rate curves and TTT diagrams of Fe–C and Fe–C–Cr alloys. Adding 3 wt pct Cr significantly retards austenite-to-pearlite transformation below about 850 K, for which a strong decrease in nucleation rate has to be invoked. In our model, the decrease in nucleation rate is attributed to Cr segregation to austenite GB. The temperature dependence is monotonic, which makes the simplistic assumption of equilibrium GB segregation plausible.

Table II Model Parameters for Nucleation in the Fe–C–Cr System (All in SI Units as Specified in List of Symbols)

Fig. 16

(a) Nucleation rate and (b) TTT diagram of Fe–0.93C,[3] and (c) nucleation rate and (d) TTT diagram of Fe–1.02C–2.89Cr.[64] For the Fe–C–Cr alloy, results with (solid lines) and without equilibrium GB segregation (dashed lines) are presented. Grain size 3.5 × 10⁻⁴ m

3.5 Examples of Higher-Order Alloys

In higher-order systems, there is much less available high-quality experimental data than in the ternary systems. We take Cr–Mn[65] (Figure 17) and Cr–Ni[66] (Figure 18) eutectoid steels, for example.

Fig. 17

(a) Growth rate, (b) lamellar spacing, (c) partition coefficients, and (d) TTT diagram of Fe–0.60C–1.05Cr–1.02Mn–0.20Si alloy. Experimental data from Ref. [65]. Grain size is assumed to be 10⁻⁴ m

Fig. 18

(a) Growth rate, (b) lamellar spacing, (c) partition coefficients, and (d) TTT diagram of Fe–0.90C–1.05Cr–1.21Ni–0.12Mn alloy. Experimental data from Ref. [66]. Grain size is assumed to be 10⁻⁴ m

In general, the model gives quite good results. The discrepancy below about 875 K is presumably due to the transformation product becoming “spiky” pearlite and bainite,[66] which are not considered in our model. The solute drag effect of Cr can also be influenced by other substitutional alloying elements. This has been recognized as “coupled solute drag effect” in the studies of austenite-to-ferrite transformation.[67] Effectively we can make the binding energy of Cr dependent on concentrations of other elements. However, the scarce and large scatter of available data do not seem to support further progress in this direction.

3.6 Release of Supersaturation Within Pearlite: Example of an Fe–C–Mn Alloy

Growth rate is determined by ferrite and cementite compositions right behind the austenite–pearlite interface. In case of optimal pearlite and parapearlite, the ferrite–cementite system does not reach full equilibrium and contains supersaturation. We presume the release of supersaturation takes place via diffusion between ferrite and cementite. This is a one-dimensional diffusion problem for which we can use DICTRA.[19]

According to Pickelsimer et al.,[30] the pearlite in Fe–0.75C–1.01Mn formed at 893 K is very close to parapearlite, which is consistent with our model calculation. Mn concentration in cementite upon further annealing at 893 K has been measured. The same problem is set up in DICTRA starting from ferrite and cementite under paraequilibrium. Figure 19 shows the temporal evolution of weight fraction of Mn in cementite from DICTRA, compared to the measurements by Pickelsimer et al. There is some uncertainty in the choice of lamellar spacing (twice the cell size in DICTRA) because the measurements by Pickelsimer et al. were carried out using carbides extracted by chemical etching, which come from all possible lamellar spacings. However, using the calculated minimal lamellar spacings assuming maximizing growth rate or maximizing dissipation rate, DICTRA simulations give good agreement to the measured time evolution of Mn concentration in cementite.

Fig. 19

Weight fraction of Mn in cementite in Fe–0.75C–1.02Mn as a function of annealing time at 893 K. Pearlite transformation is complete within about 60 s. DICTRA cell size is half of lamellar spacing, $3.6 \times 10^{ - 8}\,{\text{m}}$ if maximizing growth rate, and $4.4 \times 10^{ - 8} \,{\text{m}}$ if maximizing dissipation rate. Experimental data from Ref. [30]

This is a case where pearlite transformation completes much quicker (in ca. 60 seconds) than the subsequent release of supersaturation (in ca. 10⁵ seconds). The two processes may take place concurrently at small undercooling (low growth rate yet high diffusivity), which makes it necessary to consider back diffusion in each phase and its effect on growth rate. However, in our opinion, under most circumstances back diffusion during growth can be neglected, and the release of supersaturation within pearlite away from the transformation front is well separated from pearlite growth.

4 Discussion

4.1 Time Dependence of Growth Rate and Nucleation Rate

It has been long discovered that in alloy steels, pearlite lamellar spacing can increase over time during isothermal treatment, which makes it usually called divergent pearlite (as opposed to the “constant pearlite” considered in this work). The increase in lamellar spacing and the accompanying decrease in growth rate are the results of partitioning between pearlite and austenite, which reduces the driving force at austenite–pearlite interface.[6,25,68,69] Our model can be generalized to include divergent pearlite if partitioning between pearlite and austenite is considered.

Grain boundary nucleation rate $J^{0}$ is time-dependent even when growth rate is not. This has been verified by early painstaking extraction of nucleation rate from metallography[3,12,36] or indirect in situ measurements.[32] Alternatively, $J^{0} \left( t \right)$ can be obtained from $X\left( t \right)$ curve obtained from, e.g., dilatometry, if growth rate is reliably known. However, due to a lack of theoretical advances, there is not a reliable parameterization of $J^{0} \left( t \right)$ for pearlite, not to mention the dependences of the parameters on chemical composition. There is a need of study of nucleation kinetics as systematic as that of growth rate.

We have attempted to consider the effect of GB segregation on pearlite GB nucleation. Such effect is alluded by the effect of austenitization temperature on nucleation.[70] Compared to the steady-state modeling in this work assuming equilibrium GB segregation before pearlite starts, a better way is to include kinetics of diffusion towards GB in McLean isotherm.[34] GB composition can be measured in, e.g., atom probe tomography. For GB nucleation in a general alloy, it is fundamental to know the binding energies and interactions of segregants. There is also a call of theory of non-steady-state nucleation convoluted with the kinetics of GB with segregation. These considerations are fundamental for pearlite transformation kinetics under non-isothermal conditions and its dependence on austenitization temperature and impurity levels (P, S, etc.).

Segregation can be complex. In our model, a calibration using Cahn’s model for solute drag of Cr gives too high prefactor and activation energy for $\left( {D^{B \bot } /\delta } \right).$ This can be a result of violating the dilute solution behavior which our model assumes. The atmosphere of GB segregation can be clustered instead of being uniform if GB composition enters miscibility gap, as verified by simulation and experimental measurements.[71] This brings challenge to all available solute drag models.

Lastly, we point out that Cahn’s analysis of overall transformation kinetics should be generalized if growth rate is time-dependent.

4.2 Influence of Other Phases

In this work, we ignored any preexisting phase in austenite before pearlite forms (e.g., proeutectoid ferrite or cementite) and any phase which can precipitate during pearlite formation (e.g., carbides due to microalloying Ti, V, or Nb,[72,73,74,75] and Cu precipitation[76]) on austenite–pearlite interface or within pearlite. Preexisting phase changes the composition of austenite from which pearlite forms, hence its thermodynamic driving force. Preexisting phases also have some kinetic influences to pearlite: Proeutectoid ferrite or cementite plates can provide extra nucleation sites for pearlite. Fine precipitates can exert a pinning force to austenite–pearlite interface, lowering the interfacial mobility. The kinetics of precipitation on interface and within pearlite, if occurring concurrently with pearlite formation, greatly complicates the picture. Further experimental and theoretical work is required to quantify and model these influences, for example, quantitative studies of the effects of precipitate phase fraction and particle size on the growth rate of pearlite.

5 Conclusions

• 1. Steady-state growth of pearlite in multicomponent steel is quantitatively modeled. The model considers formation of ferrite–cementite interface, volume and boundary diffusion, finite interfacial mobility, and solute drag effect. Optimal lamellar spacing is determined by an optimization criterion, maximizing growth rate or free energy dissipation rate. The model can give growth rate, lamellar spacing, and partitioning of elements between ferrite and cementite. Model parameters are determined by calibration to binary and ternary systems.

• 2. Finite interfacial mobility is the key to avoid unphysical values of ferrite–cementite interfacial properties used in previous models assuming infinitely large interfacial mobility. The interfacial mobility has a pronounced non-Arrhenius temperature dependence which is modeled phenomenologically.

• 3. Constrained carbon equilibrium has been introduced for “optimal pearlite” as a generalization of orthoequilibrium and paraequilibrium. Optimal partitioning of substitutional alloying elements can be determined by the same optimization criterion, which realizes a smooth transition between orthopearlite and parapearlite and can describe the kinetics of pearlite growth in a wide temperature range. Such a transition is supported by partition coefficients and lamellar spacing measurements. In optimal pearlite, degree of partitioning depends on lamellar spacing, which resolves the discrepancies in partition coefficients measured in previous works. Release of supersaturation in pearlite takes place primarily by diffusion towards neighboring ferrite/cementite lamellae and is usually much slower than pearlite growth.

• 4. Solute drag effect on growth is modeled in a simple steady-state approach. Solute drag creates bays in growth rate, lamellar spacing, and partition coefficients in favor of slower growth, larger lamellar spacing, and fuller partitioning.

• 5. Grain boundary nucleation rate is modeled in a phenomenological steady-state approach. The temperature and composition dependences are calibrated to overall transformation kinetics. Effect of equilibrium grain boundary segregation is also considered.

• 6. Future work is suggested for grain boundary nucleation rate of pearlite, improved solute drag model, and effect of other phases.

Appendices

Appendix 1: Exact Analytical Expression of Solute Drag Force Using Cahn’s Model

In this work, we use Cahn’s solute drag model.[24] In this Appendix, we give the exact analytical expression of solute drag force under a wedge-shaped binding energy profile and constant diffusivity.

The binding energy profile is

$$ E\left( x \right) = \left\{\begin{array}{ll} 0,\quad x \le - \delta \\ E_{0} \left( 1 + \frac{x}{\delta} \right), \quad - \delta < x \le 0 \\ E_{0} \left( 1 - \frac{x}{\delta} \right), \quad 0 < x < \delta \\ 0, x \ge \delta \end{array}\right. $$

(A1)

The exact concentration profile is (Eq. 7 in Reference 24, after converting atomic quantities to molar quantities)

$$ c = c_{0} \exp \left\{ { - \frac{E\left( x \right)}{RT} - v\mathop \smallint \limits_{{x_{0} }}^{x} \frac{{{\text{d}}\eta }}{D\left( \eta \right)}} \right\}\mathop \smallint \limits_{ - \infty }^{x} \exp \left\{ {\frac{E\left( \xi \right)}{RT} + v\mathop \smallint \limits_{{x_{0} }}^{\xi } \frac{{{\text{d}}\eta }}{D\left( \eta \right)}} \right\}\frac{{v{\text{d}}\xi }}{D\left( \xi \right)} $$

(A2)

In Cahn’s definition, $E_{0} < 0$ for segregation, which is the opposite to $E^{b}$ defined in the main text. Concentration $c$ correspond to the $u$ fraction we use. The diffusivity $D$ is $D^{B \bot }$ in the main text. Otherwise, we can proceed with Cahn’s symbols without ambiguity.

Assuming $D\left( x \right) \equiv D,$ Eq. [A2] becomes

$$ \frac{c\left( x \right)}{{c_{0} }} = \exp \left\{ { - \frac{E\left( x \right)}{RT} - \frac{{v\left( {x - x_{0} } \right)}}{D}} \right\}\mathop \smallint \limits_{ - \infty }^{x} \exp \left\{ {\frac{E\left( \xi \right)}{RT} + \frac{{v\left( {\xi - x_{0} } \right)}}{D}} \right\}\frac{{v{\text{d}}\xi }}{D} $$

(A3)

If $v = 0,$ equilibrium segregation profile is restored: (Eq. 8, Reference 24)

$$ \frac{c\left( x \right)}{{c_{0} }} = \exp \left\{ { - \frac{E\left( x \right)}{RT}} \right\} $$

(A4)

Given the concentration profile $c\left( x \right),$ the normalized solute drag force is (Eq. 9, Reference 24)

$$ \frac{{{\Updelta}G_{m}^{\rm SD} }}{{c_{0} RT}} = - \mathop \smallint \limits_{ - \infty }^{ + \infty } \left( {\frac{c}{{c_{0} }} - 1} \right)\frac{{{\text{d}}\left( {E/RT} \right)}}{{{\text{d}}x}}{\text{d}}x $$

(A5)

In our context, $c$ is understood as u fraction, $E$ and ${\Updelta}G_{m}^{\rm SD}$ are both in J mol⁻¹. ${\Updelta}G_{m}^{\rm SD}$ is always positive.

1.1 A1. Composition Profile

Let $E_{0} /RT = p,v\delta /D = q,vx_{0} /D = q_{0} ,vx/D = qx/\delta.$ The solutions are:

Region 1: $x \le - \delta , E\left( x \right) = 0$

$$ \frac{{c_{1} \left( x \right)}}{{c_{0} }} = 1 $$

(A6)

Region 2: $- \delta < x \le 0,\frac{E\left( x \right)}{RT} = p\left( {1 + \frac{x}{\delta }} \right)$

If $p + q \ne 0,$

$$ \frac{{c_{2} \left( x \right)}}{{c_{0} }} = \frac{p}{p + q}\exp \left[ { - \left( {p + q} \right)\left( {1 + \frac{x}{\delta }} \right)} \right] + \frac{q}{p + q} $$

(A7)

If $p + q = 0,$

$$ \frac{{c_{2} \left( x \right)}}{{c_{0} }} = 1 + q\left( {1 + \frac{x}{\delta }} \right) $$

(A8)

Region 3: $0 < x < \delta ,\frac{E\left( x \right)}{RT} = p\left( {1 - \frac{x}{\delta }} \right)$

If $q + p \ne 0$ and $q - p \ne 0,$

$$ \frac{{c_{3} \left( x \right)}}{{c_{0} }} = \frac{p}{p + q}\exp \left[ { - \left( {q + p} \right) + \frac{{\left( {p - q} \right)x}}{\delta }} \right] + \left( {\frac{q}{p + q} - \frac{q}{q - p}} \right)\exp \left[ {\left( {p - q} \right)\frac{x}{\delta }} \right] + \frac{q}{q - p} $$

(A9)

If $q + p \ne 0$ and $q - p = 0,$ which means $p = q \ne 0,$

$$ \frac{{c_{3} \left( x \right)}}{{c_{0} }} = \frac{1}{2}\exp \left( { - 2q} \right) + \left( {\frac{1}{2} + \frac{qx}{\delta }} \right) $$

(A10)

If $q + p = 0$ and $q - p \ne 0,$ which means $p = - q \ne 0,$

$$ \frac{{c_{3} \left( x \right)}}{{c_{0} }} = \left( {q + \frac{1}{2}} \right)\exp \left( { - \frac{2qx}{\delta }} \right) + \frac{1}{2} $$

(A11)

If $q + p = 0$ and $q - p = 0,$ in other words $p = q = 0,$

$$ \frac{{c_{3} \left( x \right)}}{{c_{0} }} = 1 $$

(A12)

Region 4: $x > \delta , E\left( x \right) = 0$

If $p + q \ne 0$ and $q - p \ne 0,$

$$ \frac{{c_{4} \left( x \right)}}{{c_{0} }} = \frac{p}{p + q}\exp \left[ { - q\left( {1 + \frac{x}{\delta }} \right)} \right] + \left( {\frac{q}{p + q} - \frac{q}{q - p}} \right)\exp \left( {p - \frac{qx}{\delta }} \right) + \frac{p}{q - p}\exp \left[ {q\left( {1 - \frac{x}{\delta }} \right)} \right] + 1 $$

(A13)

If $p + q \ne 0$ and $q - p = 0,$ which means $p = q \ne 0,$

$$ \frac{{c_{4} \left( x \right)}}{{c_{0} }} = \frac{1}{2}\exp \left[ { - q\left( {1 + \frac{x}{\delta }} \right)} \right] + \left( {q - \frac{1}{2}} \right)\exp \left[ {q\left( {1 - \frac{x}{\delta }} \right)} \right] + 1 $$

(A14)

If $p + q = 0$ and $q - p \ne 0,$ which means $p = - q \ne 0,$

$$ \frac{{c_{4} \left( x \right)}}{{c_{0} }} = \left( {q + \frac{1}{2}} \right)\exp \left[ { - q\left( {1 + \frac{x}{\delta }} \right)} \right] - \frac{1}{2}\exp \left[ {q\left( {1 - \frac{x}{\delta }} \right)} \right] + 1 $$

(A15)

If $q + p = 0$ and $q - p = 0,$ in other words $p = q = 0,$

$$ \frac{{c_{4} \left( x \right)}}{{c_{0} }} = 1 $$

(A16)

1.2 A2. Total Solute Drag Force

The integral

$$ \mathop \smallint \limits_{ - \infty }^{ + \infty } \left( {\frac{c}{{c_{0} }} - 1} \right)\frac{{{\text{d}}\left( {E/RT} \right)}}{{{\text{d}}x}}{\text{d}}x = - \frac{{{\Updelta}G_{m}^{\rm SD} }}{{c_{0} RT}} = I $$

(A17)

is evaluated in the four regions described above. Obviously

$$ {{I}}_{1} = {{I}}_{4} = 0 $$

(A18)

If $p + q \ne 0,$

$$ I_{2} = \frac{{ - p^{2} }}{{\left( {q + p} \right)^{2} }}\left[ {\exp \left( { - p - q} \right) - 1} \right] - \frac{{p^{2} }}{p + q} $$

(A19)

If $p + q = 0,$

$$ I_{2} = \frac{{ - q^{2} }}{2} $$

(A20)

If $q + p \ne 0$ and $q - p \ne 0,$

$$ I_{3} = - \frac{{p^{2} }}{{\left( {p + q} \right)\left( {p - q} \right)}}\left[ {\exp \left( { - 2q} \right) - \exp \left( { - q - p} \right)} \right] - pq\left( {\frac{1}{p + q} - \frac{1}{q - p}} \right)\frac{1}{p - q}\left[ {\exp \left( {p - q} \right) - 1} \right] - \frac{{p^{2} }}{q - p} $$

(A21)

If $q + p \ne 0$ and $q - p = 0,$

$$ I_{3} = - \frac{q}{2}\exp \left( { - 2q} \right) + \frac{q}{2} - \frac{{q^{2} }}{2} $$

(A22)

If $q + p = 0$ and $q - p \ne 0,$

$$ I_{3} = \left( { - \frac{q}{2} - \frac{1}{4}} \right)\left[ {\exp \left( { - 2q} \right) - 1} \right] - \frac{q}{2} $$

(A23)

If $q + p = 0$ and $q - p = 0,$

$$ I_{3} = 0 $$

(A24)

The total force is then

$$ \frac{{{\Updelta}G_{m}^{\rm SD} }}{{c_{0} RT}} = - \left( {I_{1} + I_{2} + I_{3} + I_{4} } \right) $$

(A25)

1.3 A3. Low- and High-Velocity Limits, Approximate Solution

Low-velocity limit (Eq. 15, Reference 24):

$$ \left. {\frac{{\Delta G_{m}^{\rm SD} }}{{c_{0} RT}}} \right|_{v \to 0} = \frac{4v}{D}\mathop \smallint \limits_{ - \infty }^{ + \infty } \sinh^{2} \frac{E\left( x \right)}{2RT}{\text{d}}x = \frac{4v\delta }{D}\left[ {\frac{{\sinh \left( {E_{0} /RT} \right)}}{{\left( {E_{0} /RT} \right)}} - 1} \right] = k_{1} \left( {\frac{v\delta }{D}} \right) $$

(A26)

High-velocity limit (Eq. 12, Reference 24):

$$ \left. {\frac{{\Delta G_{m}^{\rm SD} }}{{c_{0} RT}}} \right|_{v \to + \infty } = \frac{{D}}{v}\mathop \smallint \limits_{ - \infty }^{ + \infty } \left[ {\frac{{\text{d}}E\left( x \right)}{{\text{d}}x}} \right]^{2} {\text{d}}x = 2\left( {\frac{{E_{0} }}{RT}} \right)^{2} \left( {\frac{v\delta }{{D}}} \right)^{ - 1} = k_{2} \left( {\frac{v\delta }{{D}}} \right)^{ - 1} $$

(A27)

Cahn has constructed an approximate solution which connects low- and high-velocity limits (Eqs. 16–18, Reference 24). Using the $k_{1}$ and $k_{2}$ coefficients defined in the previous two equations, the expression is:

$$ \frac{{\Delta G_{m}^{\rm SD} }}{{c_{0} RT}} \cong \frac{{k_{1} \left( {\frac{v\delta }{D}} \right)}}{{1 + \frac{{k_{1} }}{{k_{2} }}\left( {\frac{v\delta }{D}} \right)^{2} }} $$

(A28)

which is the same as Cahn’s expressions with his $\alpha$ and $\beta^{2}$ coefficients (his expression of $\alpha$ in an unnamed equation between 21 and 22 has a missing $4\delta$ in the numerator).

1.4 A4. Plots

Figures A1 and A2 show that the analytical expressions of composition profile and solute drag force give identical results to numerical integrations. Figure A2 shows that although the approximation is accurate at the low- and high-velocity limits, it gives higher solute drag force than the exact solution, similarly shown by Cahn (Figure 4 in Reference 24).

Fig. A1

Concentration profiles with (a) $E_{0} /RT = - 2$ (segregation) and (b) $E_{0} /RT = 2$(anti-segregation), and $v\delta /D = 0, 1 , 3, 10.$ Solid lines from analytical expression. Open circles from numerical integration of Eq. [A3], giving values identical to those from the analytical expression

Fig. A2

Solute drag force for $E_{0} /RT = \pm 2.$ Solid line from analytical expression. Open circles from numerical integration of Eq. [A5], giving values identical to those from analytical expression. Low- and high-velocity limits (Eqs. [A26] and [A27]) and the approximation Eq. [A28] are also shown

Figure A3 shows some properties of the maximal solute drag force. At the low-segregation limit $\left( {{\Updelta}G_{m}^{\rm SD} /c_{0} RT} \right)_{ \hbox{max} } \propto \left( {E_{0} /RT} \right)^{2}.$ From low to high segregation, the position of maximum $v_{0} \delta /D$ moves from approximately 1.9 to 1.0.

Fig. A3

(a) Maximal solute drag force $\left( {\Delta G_{m}^{\rm SD} /c_{0} RT} \right)_{ \hbox{max} }$and (b) value of $v_{0} \delta /D$ at maximal solute drag force, as functions of $E_{0} /RT.$

Appendix B: Detailed Derivation of Dissipation by Diffusion

The geometry of the diffusion field is shown in Figure 1. Due to symmetry, we consider an area $S/2$ wide and unit length deep on the austenite–pearlite interface. The ferrite-to-austenite and cementite-to-austenite atomic fluxes of element $i$ are

$$ \begin{aligned} J_{i}^{\alpha \to \gamma } & = \left( {u_{i}^{0} - u_{i}^{\alpha } } \right)v\frac{S}{2}\left( {1 - f^{\theta } } \right) \hfill \\ J_{i}^{\theta \to \gamma }& = \left( {u_{i}^{0} - u_{i}^{\theta } } \right)v\frac{S}{2}f^{\theta } \hfill \\ \end{aligned} $$

(B1)

Because there is no net flux from pearlite to austenite, the incoming flux to austenite must make a U-turn and equal the outgoing flux from austenite. Considering the fraction of ferrite and cementite at the interface, the flux is

$$ J = J_{i}^{\alpha \to \gamma } = - J_{i}^{\theta \to \gamma } $$

(B2)

Now we consider how the flux distributes and the amount of dissipation.

From diffusion theory,[77] flux J is driven by negative gradient of chemical potential. At one point in a continuous diffusion field with local flux density j and chemical potential $\mu,$ the free energy dissipation rate density, namely the free energy dissipation per unit volume per unit second, is $- \vec{j} \cdot \vec{\nabla }\mu.$ Here the arrow refers to real space instead of composition space. Also from diffusion theory, $\overrightarrow {{j_{i} }} = u_{i} M_{i} \left( { - \vec{\nabla }\mu_{i} } \right)$ if we neglect cross-terms in composition space, where $M_{i}$ is the atomic mobility of element $i$ at this space. As a result, the dissipation rate density is $j^{2} /u_{i} M_{i}.$

2.1 B1. Volume Diffusion Only

The driving force of diffusion is approximately

$$ \frac{{\text{d}}\mu }{{\text{d}}z} \cong \frac{{\mu^{\alpha } - \mu^{\theta } }}{S/2} $$

(B3)

Now we make the same approximation as Zener for concentration profile in austenite: We assume the flux is perpendicular to the ferrite–cementite interface, spanning over $S/2$ in the z direction and distributed over the same length in the x direction, as a constant.

Flux density is

$$ j_{V} = \frac{J}{S/2} $$

(B4)

They are connected by

$$ j_{V} = u_{i}^{0} M_{i}^{\gamma } \left( { - \frac{{\text{d}}\mu }{{\text{d}}z}} \right) $$

(B5)

The total dissipation rate is

$$ \frac{S}{2}\mathop \smallint \limits_{0}^{S/2} j_{V} \left( { - \frac{{\text{d}}\mu }{{\text{d}}z}} \right){\text{d}}z = \frac{S}{2}\mathop \smallint \limits_{0}^{S/2} \frac{{j_{V}^{2} }}{{u_{i}^{0} M_{i}^{\gamma } }}{\text{d}}z = \frac{{J^{2} }}{{u_{i}^{0} M_{i}^{\gamma } }} $$

(B6)

We neglect the details of composition and flux distribution in space and composition dependence of atomic mobility, and simply take $M_{i}^{\gamma }$ from bulk austenite composition.

2.2 B2. Boundary Diffusion Only

In this case we assume diffusion only takes place within austenite–pearlite interface whose width is $\delta.$ Compared to the volume diffusion-only case, in the x direction the cross section should change from $S/2$ to $\delta.$

$$ \begin{aligned} j_{B} & = \frac{J}{\delta } \hfill \\ j_{B} & = u_{i}^{\rm B} M_{i}^{\rm B} \left( { - \frac{{\text{d}}\mu }{{\text{d}}z}} \right) \hfill \\ \end{aligned} $$

(B7)

where $u_{i}^{\rm B}$ and $M_{i}^{B\parallel }$ are boundary concentration and in-plane atomic mobility, respectively. In literature it is common to write $u_{i}^{\rm B} = ku_{i}^{0}$ where $k$ is a segregation factor. The total dissipation rate is

$$ \delta \mathop \smallint \limits_{0}^{S/2} j_{B} \left( { - \frac{{\text{d}}\mu }{{\text{d}}z}} \right){\text{d}}z = \delta \mathop \smallint \limits_{0}^{S/2} \frac{{j_{B}^{2} }}{{u_{i}^{\rm B} M_{i}^{B\parallel } }}{\text{d}}z = \frac{{J^{2} }}{{u_{i}^{0} M_{i}^{B\parallel } }}\frac{S}{2\delta } $$

(B8)

2.3 B3. Combined

A more realistic consideration is to include both volume diffusion and boundary diffusion. They are driven by the same driving force (Eq. [B3]) but their fluxes must add up to the total flux (Eq. [B2]). This is analogous to a parallel combination of two resistors under the same voltage.[40]

$$ \begin{aligned} J & = j_{V} \frac{S}{2} + j_{B} \delta \\ \frac{{j_{V} }}{{u_{i}^{0} M_{i}^{\gamma } }} & = \frac{{j_{B} }}{{u_{i}^{0} kM_{i}^{B\parallel } }} = \left( { - \frac{{{\text{d}}\mu }}{{{\text{d}}z}}} \right) \\ \end{aligned} $$

(B9)

The total dissipation rate of the system is

$$ \frac{S}{2}\mathop \smallint \limits_{0}^{S/2} j_{V} \left( { - \frac{{\text{d}}\mu }{{\text{d}}z}} \right){\text{d}}z + \delta \mathop \smallint \limits_{0}^{S/2} j_{B} \left( { - \frac{{\text{d}}\mu }{{\text{d}}z}} \right){\text{d}}z = \frac{{J^{2} }}{{u_{i}^{0} \left[ {M_{i}^{\gamma } + \frac{{2\left( {kM^{B\parallel } \delta } \right)_{i} }}{S}} \right]}} = v^{2} \left( {\frac{{Sf^{\theta } }}{2}} \right)^{2} \frac{{\left( {u_{i}^{0} - u_{i}^{\theta } } \right)^{2} }}{{u_{i}^{0} \left[ {M_{i}^{\gamma } + \frac{{2\left( {kM^{B\parallel } \delta } \right)_{i} }}{S}} \right]}} $$

(B10)

From which we can use the dimensionless ratio $r \equiv 2\left( {kM^{B\parallel } \delta } \right)_{i} /M_{i}^{\gamma } S$ to characterize the relative significance of boundary and volume diffusion: $r = 0$ for volume diffusion only, $r \to + \infty$ for boundary diffusion only.

The friction force caused by diffusional dissipation, in the unit of molar energy, is the total dissipation rate divided by velocity $v$ and the interface area $S/2.$

$$ \frac{{vS\left( {f^{\theta } } \right)^{2} }}{2}\frac{{\left( {u_{i}^{0} - u_{i}^{\theta } } \right)^{2} }}{{u_{i}^{0} \left[ {M_{i}^{\gamma } + \frac{{2\left( {kM^{B\parallel } \delta } \right)_{i} }}{S}} \right]}} $$

(B11)