Deformation of a Convex Hydrogel Shell by Parallel Plate and Central Compression

Abstract

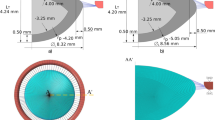
To characterize the materials parameters and deformation of a convex shell of axial symmetry, a hydrogel contact lens is mechanically deformed by two loading configurations: (a) compression between two parallel plates and (b) central load applied by a shaft with a spherical tip. A universal testing machine with nano-Newton and submicron resolutions is used to measure the applied force, F, as a function of vertical displacement of the plate/shaft, w ₀, while a homemade laser aided topography system records the in-situ deformed shell profile and the contact radius or central dimple, a. A nonlinear shell theory and an iterative finite difference method are used to account for the large elastic deformation, the central buckling for the central load compression, and the interrelationship between the measureable quantities (F, w ₀, a).

Appendix

Nomenclature

ϕ₀ :

angle between the outer normal of shell element and symmetry axis of non-deformed shell

ϕ:

angle between the outer normal of shell element and symmetry axis of deformed shell

$\phi^{*}_{0}$ :

denotes value of ϕ₀ at the contact edge

$\phi^{\dag}_{0}$ :

denotes value of ϕ₀ at the base of the shell

β:

rotation of normal

r ₀ :

distance from symmetry axis before deformation

R :

radius of undeformed shell

c :

radius of the base of the shell

E :

Young’s modulus

v :

Poisson’s ratio

t :

thickness of shell

K :

Et / (1- v ²)

D :

Et ³/ 12(1- v ²)

F :

total load on shell

${{\text{e}}_\phi },{{\text{e}}_\theta }$ :

meridional and circumferential strain

${{\text{k}}_\phi },{{\text{k}}_\theta }$ :

meridional and circumferential bending curvature

w, u :

deflection parallel and perpendicular to axis of symmetry

V, H :

stress resultants parallel and perpendicular to axis of symmetry

p _V , p _H :

surface loads parallel and perpendicular to axis of symmetry

${N_\phi },{N_\theta }$ :

meridional and circumferential stress resultants

${M_\phi },{M_\theta }$ :

meridional and circumferential moment resultant

Q :

transverse shear resultants

Numerical Method

Finite difference method is employed here to solve this boundary boundary-value problem governed by a system of first order ordinary differential equations (ODE) [27]. A two point boundary value problem in the interval I = [c ₁, c ₂] can be defined by a system of first-order ODEs and boundary conditions as follows.

$$ \frac{{dy({\varphi_0})}}{{d{\varphi_0}}} = f\left( {{\varphi_0},y({\varphi_0})} \right)\quad {\text{and}}\quad {r_B}\left( {y({c_1}),y({c_2})} \right) = 0 $$

(17)

The interval I is divided into M segments uniformly and the choice of M should be a sufficiently large number to guarantee the accuracy of the solution. I _m  = [c _m-1, c _m ] denotes one specific segment where m = 1…M. For the shell problem described by equations (1-5), the boundary-value problem is stated in terms of the six unknowns, y = {w u β V H  M _ϕ}. Equations (1-5) are rearranged in the form in equation (17) as follows.

$$ \begin{array}{*{20}{c}} {\frac{{dw}}{{d{\varphi_0}}} = R\left( {{\varepsilon_\varphi }\sin \varphi - {\kappa_\theta }{r_0}} \right)} \\ {\frac{{du}}{{d{\varphi_0}}} = R\left( {{ }{\varepsilon_\varphi }\cos \varphi + 2\sin (\beta /2)\sin ({\varphi_0} - \beta /2){ }} \right)} \\ {\frac{{d\beta }}{{d{\varphi_0}}} = R{\kappa_\varphi }} \\ {\frac{{dV}}{{d{\varphi_0}}} = - \frac{{{r_1}}}{r}V - \alpha {p_V}} \\ {\frac{{dH}}{{d{\varphi_0}}} = - \frac{{{r_1}}}{r}H + \frac{{\alpha {N_\theta }}}{r} - \alpha {p_H}} \\ {\frac{{d{M_\varphi }}}{{d{\varphi_0}}} = - \frac{{{r_1}}}{r}{ }{M_\varphi } + \frac{{\alpha \cos \varphi }}{r}{M_\theta } - \alpha \left( {H\sin \varphi - V\cos \varphi } \right)} \\ \end{array} $$

(18)

Using the (implicit) trapezoidal rule, the residual vector ${\psi_m}$ for a segment I _m is defined as follows.

$$ {\psi_m}\left( {{y_m},{y_{m - 1}}} \right) = \frac{{{y_m} - {y_{m - 1}}}}{{\Delta {\varphi_0}}} - \frac{1}{2}\left[ {f\left( {{\varphi_{m - 1}},{y_{m - 1}}} \right) + f\left( {{\varphi_m},{y_m}} \right)} \right] = 0 $$

(19)

where ϕ _m represents the terms on the right hand side of equation (18). Considering the finite difference segmentation of the entire shell one would get (M + 1) vector equations for the (M + 1) vectors y ₀, y ₁, …, y _M each having 6 unknowns. For the solution of the large system of non-linear equations (19), Newton’s method is employed. A multivariable Taylor series expansion of the residual form of equation (19) is used to linearize the system. When all of the segments are considered the system of equations is expressed in the following form.

$$ {[D{\psi_y}]^{(i)}}{\{ \Delta y{\text{\} }}^{(i + 1)}} = - {\{ \psi \}^{(i)}} $$

(20)

where the superscript i indicates solution iteration level, and {∆y}⁽ⁱ⁺¹⁾ is the correction to the dof vector between the iterations. The Jacobian matrix D ψ _y is defined as

$$ D{\psi_y} = \left[ {\begin{array}{*{20}{c}} { - \left[ {I + \frac{{\Delta {\varphi_1}}}{2}{{\left( {\frac{{\partial f}}{{\partial {y_0}}}} \right)}_{{\varphi_0}}}} \right]} & {\left[ {I - \frac{{\Delta {\varphi_1}}}{2}{{\left( {\frac{{\partial f}}{{\partial {y_1}}}} \right)}_{{\varphi_1}}}} \right]} & {} & {} & {} \\ {} & { - \left[ {I + \frac{{\Delta {\varphi_2}}}{2}{{\left( {\frac{{\partial f}}{{\partial {y_1}}}} \right)}_{{\varphi_1}}}} \right]} & {\left[ {I - \frac{{\Delta {\varphi_2}}}{2}{{\left( {\frac{{\partial f}}{{\partial {y_2}}}} \right)}_{{\varphi_2}}}} \right]} & {} & {} \\ {} & {} & \ddots & \ddots & {} \\ {} & {} & { - \left[ {I + \frac{{\Delta {\varphi_M}}}{2}{{\left( {\frac{{\partial f}}{{\partial {y_{M - 1}}}}} \right)}_{{\varphi_{m - 1}}}}} \right]} & {\left[ {I - \frac{{\Delta {\varphi_M}}}{2}{{\left( {\frac{{\partial f}}{{\partial {y_M}}}} \right)}_{{\varphi_m}}}} \right]} & {} \\ {\frac{{\partial r}}{{\partial {y_0}}}} & {} & {} & {\frac{{\partial r}}{{\partial {y_M}}}} & {} \\ \end{array} } \right] $$

(21)

To calculate Jacobian matrix (21), equation (18) is differentiated with respect to each of the unknown variables, i.e. {w u β V H  M _ϕ}^T. The prime below denotes derivative respect to any one of the six variables_. Thus,

$$ \begin{gathered} \begin{array}{*{20}{c}} {\frac{{dw\prime }}{{d{\varphi_0}}} = \alpha \prime \sin \varphi + \alpha \varphi \prime \cos \varphi } \\ {\frac{{du\prime }}{{d{\varphi_0}}} = \alpha \prime \cos \varphi + \alpha \varphi \prime \sin \varphi } \\ {\frac{{d\beta \prime }}{{d{\varphi_0}}} = R\kappa_\varphi^\prime } \\ {\frac{{dV\prime }}{{d{\varphi_0}}} = - \frac{{r_1^\prime }}{r}{ }V - \frac{{{r_1}}}{r}V\prime + \frac{{{r_1}r\prime }}{{{r^2}}}V - \alpha \prime {p_V}} \\ {\frac{{dH\prime }}{{d{\varphi_0}}} = - \frac{{r_1^\prime }}{r}H - \frac{{{r_1}}}{r}H\prime + \frac{{{r_1}r\prime }}{{{r^2}}}H + \frac{{\alpha \prime {N_\theta }}}{r}{ } + { }\frac{{\alpha N_\theta^\prime }}{r} - \frac{{\alpha r\prime {N_\theta }}}{{{r^2}}} - \alpha \prime {p_H}} \\ {\frac{{dM_\varphi^\prime }}{{d{\varphi_0}}} = - { }\frac{{r_1^\prime {M_\varphi }}}{r}{ } - { }\frac{{{r_1}M_\varphi^\prime }}{r}{ } + { }\frac{{{r_1}r\prime }}{{{r^2}}}{M_\varphi } + \frac{{\alpha \prime \cos \varphi }}{r}{M_\theta } - \frac{{\alpha { }\varphi \prime \sin \varphi }}{r}{ }{M_\theta } + \frac{{\alpha \cos \varphi }}{r}M_\theta^\prime - \frac{{\alpha { }r\prime \cos \varphi }}{{{r^2}}}{M_\theta } - \alpha \prime H\sin \varphi - \alpha H\prime \sin \varphi - \alpha H{ }\varphi \prime \cos \varphi + \alpha \prime V\cos \varphi + \alpha V\prime \cos \varphi + \alpha V{ }\varphi \prime \sin \varphi } \\ \end{array} \hfill \\ \frac{{dM_\varphi^\prime }}{{d{\varphi_0}}} = - \frac{{r_1^\prime {M_\varphi }}}{r} - \frac{{{r_1}M_\varphi^\prime }}{r} + \frac{{{r_1}r\prime }}{{{r^2}}}{M_\varphi } + \frac{{\alpha \prime \cos \varphi }}{r}{M_\theta } - \frac{{\alpha { }\varphi \prime \sin \varphi }}{r}{ }{M_\theta } + \frac{{\alpha \cos \varphi }}{r}M_\theta^\prime - \frac{{\alpha { }r\prime \cos \varphi }}{{{r^2}}}{M_\theta } - \alpha \prime H\sin \varphi - \alpha { }H\prime \sin \varphi - \alpha { }H{ }\varphi \prime \cos \varphi + \alpha \prime V\cos \varphi + \alpha { }V\prime \cos \varphi + \alpha { }V{ }\varphi \prime \sin \varphi \hfill \\ \end{gathered} $$

(22)

where

$$ \begin{array}{*{20}{c}} {\varepsilon_\theta^\prime = u\prime /{r_0}} \\ {\varphi \prime = - \beta \prime } \\ {\kappa_\theta^\prime = - { }\varphi \prime \cos \varphi /{r_0}} \\ {{N_\varphi } = { }H\prime \cos \varphi { } - { }H\varphi \prime \sin \varphi + V\prime \sin \varphi + V\varphi \prime \cos \varphi } \\ {\varepsilon_\varphi^\prime = N_\varphi^\prime /K - \nu \varepsilon_\theta^\prime } \\ {\kappa_\varphi^\prime = M_\varphi^\prime /D - \nu \kappa_\theta^\prime } \\ {N_\theta^\prime = K\left( {\varepsilon_\theta^\prime + \nu \varepsilon_\theta^\prime } \right)} \\ {M_\theta^\prime = D\left( {\kappa_\theta^\prime + \nu \kappa_\theta^\prime } \right)} \\ {\alpha \prime = R\varepsilon_\varphi^\prime } \\ {r\prime = u\prime } \\ {r_1^\prime = \alpha \prime \cos \varphi - \alpha { }\varphi \prime \sin \varphi } \\ \end{array} $$

The solution algorithm is shown in Fig. 6, a constant relaxation coefficient C, with a value between 0 and 1, is employed in some cases to help converge.

Fig. 6

Algorithm for finite difference computation