Star-Structure Network Coding for Multiple Unicast Sessions in Wireless Mesh Networks

Abstract

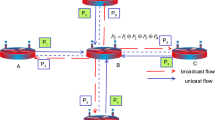
In this paper, first, we propose Star-NC, a new network coding (NC) scheme for multiple unicast sessions in an n-input n-output star structure. Then, we evaluate the network throughput of this coding scheme in wireless mesh network over the traditional non-NC transmission. Our scheme benefits from the proximity of all the nodes around the relay node and employs a more general form of overhearing different from other schemes such as COPE. We found that the gain of our NC scheme depends on both the star size and the routing pattern of the unicast transmissions. Based on this, we identify both the situations which the maximum gain is achievable and a lower bound for the expected value of the gain in the case of random routing pattern. Next, we propose an analytical framework for studying throughput gain of our Star-NC scheme in general wireless network topologies. Our theoretical formulation via linear programming provides a method for finding source-destination routes and utilizing the best choices of our NC scheme to maximize the throughput. Finally, we evaluate our model for various networks, traffic models and routing strategies over coding-oblivious routing. We also compare the throughput gain of our scheme with COPE-type NC scheme. We show that Star-NC exploits new coding opportunities different from COPE-type NC and thus can be used with or without this scheme. The results show that Star-NC has often better performance than COPE for a directional traffic model which is a typical model in wireless mesh networks. Moreover, we found that, joint Star and COPE-type NC has better throughput performance than each of Star or COPE alone.

Appendix A: Proof for Theorem 1

We explore a sufficient condition for Theorem 1 by proper selection of $\mathbf{Q}_{{\varvec{M}}}$ and $\mathbf{Q}_{{\varvec{B}}}$ in which every output nodes is capable of decoding its packet. The output node $D_{k}$ has a system of $\eta$ linear equations, out of which $\eta -m$ of them are received from the relay node’s encoded packets ($\mathbf{Q}_{{\varvec{M}}})$ and the others are captured by opportunistic listening of neighbor nodes. Therefore, it suffices to show that each output node has enough information to solve its system and decode all of the packets. This condition, for $k>m$, represents a feature of $\mathbf{Q}_{{\varvec{M}}}$ in which the deletion of the columns $i_{k-m}$through $i_{k-1}$ results a non-zero determinant matrix. However, for $k\le m$ this deletion is occurred for the columns $i_1$to $i_k$ of the union of $\mathbf{Q}_{{\varvec{M}}}$ and a matrix formed by the first $m-k$ rows of $\mathbf{Q}_{{\varvec{B}}}$, and must lead to a non-zero determinant matrix. Next, we use this condition and try to present a constructive proof for Theorem 1 by seeking suitable $\mathbf{Q}_{{\varvec{M}}}$ and $\mathbf{Q}_{{\varvec{B}}}$.

Case m $\mathbf{=1 :}$ Consider $\mathbf{Q}_{{\varvec{M}}}$ and $\mathbf{Q}_{{\varvec{B}}}$ matrices as:

$$\begin{aligned} \mathbf{Q}_{{\varvec{M}}} =\left( {{\begin{array}{l} {{\begin{array}{l} \mathbf{1} \\ 0 \\ \vdots \\ \end{array} }} \\ {0} \\ \end{array} }{\begin{array}{l} {{\begin{array}{l} 0 \\ \mathbf{1} \\ \vdots \\ \end{array} }} \\ {0} \\ \end{array} }{\begin{array}{l} {{\begin{array}{l} \cdots \\ \cdots \\ \ddots \\ \end{array} }} \\ {\cdots } \\ \end{array} }{\begin{array}{l} {{\begin{array}{l} 0 \\ 0 \\ \vdots \\ \end{array} }} \\ {\mathbf{1}} \\ \end{array} }{\begin{array}{l} {{\begin{array}{l} {1} \\ {1} \\ {\vdots } \\ \end{array} }} \\ {1} \\ \end{array} }} \right) _{(\eta -1)\times \eta } \quad \mathbf{Q}_B =I_\eta \end{aligned}$$

(22)

For any $\eta$ (even for $\eta >3m+2)$, deletion of each column of $\mathbf{Q}_{{\varvec{M}}}$ produces a non-zero determinant rectangular matrix.

Case m $\mathbf{=2 :}$ For $\eta \ge 4$, Consider $\mathbf{Q}_{{\varvec{M}}}$ as concatenation of the identity matrix of size $\eta -2$ and a two-columns matrix $J$, i.e. $\mathbf{Q}_{{\varvec{M}}} =\left( {\mathbf{I}_{\left( {\eta -2} \right) } \text{| }\mathbf{J}_{\left( {\eta -2} \right) \times 2} } \right)$ where, for different values of $\eta$, $J$ is defined as in Table 3. Now, we seek for the pairs of $\mathbf{Q}_{{\varvec{M}}}$ columns whose deletion produces a zero determinant matrix. This happens in two different cases as either the generation a row of zero elements or remaining a set of linearly dependent columns. Note that, since the first part of $\mathbf{Q}_{{\varvec{M}}}$ is an identity matrix, it has no linearly dependent rows and thus the deletion a pair of columns (except for $\eta$ =4) does not leave a matrix with dependent rows. For simple verification, we define tow terms $ZR(\mathbf{Q}_{{\varvec{M}}})$ and $CD(\mathbf{Q}_{{\varvec{M}}})$ to denote the sets containing the tuples of the columns of $\mathbf{Q}_{{\varvec{M}}}$. In the former, each tuple refers to the columns of $\mathbf{Q}_{{\varvec{M}}}$ whose deletion creates a row of zeros, while in the latter, it refers to the columns whose sum is a zero vector. For $ZR({\mathbf{Q}}_{{\varvec{M}}})$, we consider in tuples with at most two elements while for $CD({\mathbf{Q}}_{{\varvec{M}}})$ the tuples with at most $\eta -2$ elements are concerned. By a little effort, we can compute these sets, shown in Table 3, for the above $\mathbf{Q}_{{\varvec{M}}}$. Let $D_\eta ^2 (Q_M )$ denotes a set of column pairs of $\mathbf{Q}_{{\varvec{M}}}$ whose deletion results a zero determinant matrix. We can write:

$$\begin{aligned} D_\eta ^2 (Q_M )=ZR( {Q_{M}})\mathop \cup \nolimits \left\{ { \left( {i,j} \right) |\exists x\in CD(Q_M ):x\subseteq \left( {1,2,\ldots ,\eta } \right) -\left( {i,j} \right) \} } \right. \end{aligned}$$

(23)

Now, we try to find a relation between the ability of decoding for each target permutation and $D_\eta ^2 (Q_M )$. We define a target permutation as Q$_\mathrm{M}$-proper if its first $\eta -1$ elements do not include any pair of $D_\eta ^2 (Q_M )$ as two consecutive elements. This condition guaranties the feasibility of decoding for output nodes $D_3$ through $D_\eta$. Obviously, only a subset of the permutations will be Q$_\mathrm{M}$-proper. For each the others, we try to exchange the columns of $\mathbf{Q}_{{\varvec{M}}}$ in a way that it becomes a proper permutation for the altered $\mathbf{Q}_{{\varvec{M}}}$. The main idea is that we exchange of the columns based on the mapping which converts a non-proper permutation to a proper one. For instance, let $\rho =\left( {1,2,7,6,8,5,4,3} \right)$ and $\pi =\left( {6,5,1,2,8,3,7,4} \right)$, it is simple to verify that $\rho$ is Q$_\mathrm{M}$-proper, but $\pi$ is not. Now, we can create a new matrix $\acute{\mathbf{Q}}_{M}$ from $\mathbf{Q}_{{\varvec{M}}}$ by the following exchanges:

$$\begin{aligned} X_{\rho \rightarrow \pi } =\left( {1\leftrightarrow 6,2\leftrightarrow 5,7\leftrightarrow 1,6\leftrightarrow 2,8\leftrightarrow 8,5\leftrightarrow 3,4\leftrightarrow 7,3\leftrightarrow 4} \right) \end{aligned}$$

Now, $\pi$ is a $\acute{\mathbf{Q}}_{{{\varvec{M}}}}$-proper permutation. We refer to $\rho$ as generator of $\pi$. It seems that a single Q$_\mathrm{M}$-proper generator, like $\rho$, is enough for all target permutation. However, we have not verified the ability of decoding for the output nodes $D_{1}$ and $D_{2}$ yet. Indeed, these nodes overhear the input nodes $S_{1}$ and $S_{2}$ and thus decoding process is further dependent on $\mathbf{Q}_{{\varvec{B}}}$. We fix our choices of $\mathbf{Q}_{{\varvec{B}}}$ to an upper triangular matrix with elements of 1 in the main diagonal and all rows expect the second one. This $\mathbf{Q}_{{\varvec{B}}}$ implies that every input node $S_{i}$ ($i\ne 2)$ sends the encoded packet $\mathop \sum \nolimits _{k=i}^\eta P_k$ to the relay node, i.e., $S_{i}$ needs to overhear the transmissions of $S_{i+1}$ and $S_{i+2}$.

Table 3 $J_{(\eta -2)\times \eta }$, $ZR({Q}_M )$ and $CD({Q}_M )$ for $m=2$

On the other hand, since both $D_{1}$ and $D_{2}$ can overhear transmission of $S_{1}$, i.e., the encoded packet $\mathop \sum \nolimits _{i=1}^\eta P_i$. In addition to this packet, $D_{1}$ overhears the native packets $P_2$ and $D_{2}$ overhears $P_{\pi (1)}$. According to the overheard information, the decoding of $D_{1}$ and $D_{2}$ reaches to system of equations whose core is a matrix resulted from $\mathbf{Q}_{{\varvec{M}}}$ (or $\acute{\mathbf{Q}}_{{{\varvec{M}}}}$ by adding a row of 1 and deleting the column either 2 (for $D_{1})$ or $\pi ({1})$ (for $D_{1})$. Thus, it is enough to consider the effect of a column deletion in to account either for creation of a row with zero elements or for remaining a set of dependent columns. Since $ZR(Q_M )$ contains only the tuples of size 2, zeroing a row is not taken by a single column deletion. Further, since the core matrix has a row full of 1, generation a set of dependent column only is occurred for the even tuples of $CD(Q_M )$. As for $\eta =4$ and $\eta =6, CD(Q_M)$ has no even size tuples, the resulting matrices do not have any dependent columns, and hence is suitable for any target permutation. But for $\eta =5,7$ and 8, the resulting matrices have inherited the even size column dependencies of $\mathbf{Q}_{{\varvec{M}}}$. Thus, the decoding process could be done if the deletion is occurred for a column among these tuples.

We satisfy this condition by selecting a suitable Q$_\mathrm{M}$-proper generator $\rho$ for each $\pi$ in a manner that both the columns mapped to $2$ and $\pi [1]$ via $X_{\rho \rightarrow \pi }$, are picked up from these tuples. By selecting $\rho$ such that $\rho [1]=1,$ the condition related to column $\pi [1]$ is met since the first column is appeared in of all the mentioned tuples. The other condition, corresponding to columns 2, is satisfied by choosing a $\rho$ that the elements of each dependent tuple are located in even positions of $\rho$ when the position of 2 in $\pi$ is even and vice versa when the position of 2 in $\pi$ is odd. Thus, one of the following options is suitable for the generator permutation:

Position of 2 in $\varvec{\pi }$	$\varvec{\eta } =\mathbf{5}$	$\varvec{\eta } =\mathbf{7}$	$\varvec{\eta } =\mathbf{8}$
odd	$\left( {\mathbf{1},4,\mathbf{5},3,\mathbf{2}} \right)$	$(\mathbf{1},3,\mathbf{2},4,\mathbf{6},5,7)$	$(\mathbf{1},2,\mathbf{3},4,\mathbf{8},6,\mathbf{7},5)$
Even	$(1,\mathbf{4},5,\mathbf{2},3)$	$(1,\mathbf{2},3,\mathbf{6},4,\mathbf{7},5)$	$(1,\mathbf{2},3,\mathbf{4},6,\mathbf{7},5,\mathbf{8})$

Lastly, for $\text{ m }=3$ and $\text{ m }=4$, we used an extension of the method for $\text{ m }=2$ with a subtle difference that the most of verification steps is done by a computerized program. This is due to largeness of state space of the problem. The details of proof are deleted for the lack of space.