A bridge from ruin theory to credit risk

Abstract

The structural model uses the firm-value process and the default threshold to obtain the implied credit spread. Merton’s (J Finance 29:449–470, 1974) credit spread is reported too small compared to the observed market spread. Zhou (J Bank Finance 25:2015–2040, 2001) proposes a jump-diffusion firm-value process and obtains a credit spread that is closer to the observed market spread. Going in a different direction, the reduced-form model uses the observed market credit spread to obtain the probability of default and the mean recovery rate. We use a jump-diffusion firm-value process and the observed credit spread to obtain the implied jump distribution. Therefore, the discrepancy in credit spreads between the structural model and the reduced-form model can be removed. From the market credit spread, we obtain the implied probability of default and the mean recovery rate. When the solvency-ratio process in credit risk and the surplus process in ruin theory both follow jump-diffusion processes, we show a bridge between ruin theory and credit risk so that results developed in ruin theory can be used to develop analogous results in credit risk. Specifically, when the jump is Logexponentially distributed, it results in a Beta distributed recovery rate that is close to market experience. For bonds of multiple seniorities, we obtain closed-form solutions of the mean and variance of the recovery rate. We prove that the defective renewal equation still holds, even if the jumps are possibly negative. Therefore, we can use ruin theory as a methodology for assessing credit ratings.

Appendices

Appendix

The infinite time defective renewal

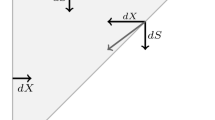
We now derive an extended defective renewal equation when the jumps are possibly negative. In this section, we assume the riskless rate r is constant. By the law of total probability, we have

$$ \begin{aligned} \phi\left(\ln\left({\frac{V_0}{D}}\right)\right)=(1-\lambda dt)\int_{Z(dt)}\phi\left[\ln\left({ \frac{V_0}{D}}\right)+\left(r-\frac{\sigma^2}{2}-\lambda\mu_J\right)dt+\sigma Z(dt)\right]dt \\ +\lambda dt \int_{-\infty}^{\ln\left({ \frac{V_0}{D}+(r-\frac{\sigma^2}{2}-\lambda\mu_J)dt+\sigma Z(dt)}\right)}\phi\left(\ln\left({ \frac{V_0}{D}}\right)+\left(r-\frac{\sigma^2}{2}-\lambda\mu_J\right)dt+\sigma Z(dt)-x\right)dF(x). \end{aligned} $$

This equation shows that the probability of survival is equivalent to the sum of the probability of survival given no jump in the small time interval (t, t + dt] and the probability of survival given a jump in the small time interval (t, t + dt] given that the jump is smaller than that will cause ruin. We have

$$ \begin{aligned} \phi\left(\ln\left({\frac{V_0}{D}}\right)\right)=(1-\lambda dt)\hbox{E}_t^Q\left\{\phi\left[\ln\left({ \frac{V_0}{D}}\right)+\left(r-\frac{\sigma^2}{2}-\lambda\mu_J\right)dt+\sigma Z(dt)\right]\right\}\\ +\lambda dt \int_{-\infty}^{\ln\left({ \frac{V_0}{D}+(r-\frac{\sigma^2}{2}-\lambda\mu_J)dt+\sigma Z(dt)}\right)}\phi\left(\ln\left({ \frac{V_0}{D}}\right)+\left(r-\frac{\sigma^2}{2}-\lambda\mu_J\right)dt+\sigma Z(dt)-x\right)dF(x). \end{aligned} $$

(24)

We can express the expected value of survival probability through Taylor expansion as

$$ \begin{aligned} \hbox{E}_t^Q & \left\{\phi\left[\ln\left({ \frac{V_0}{D}}\right)+\left(r-\frac{\sigma^2}{2}-\lambda\mu_J\right)dt+\sigma Z(dt)\right]\right\}\\ &=\phi\left(\ln\left({\frac{V_0}{D}}\right)\right)+\left(r-\frac{\sigma^2}{2}-\lambda\mu_J\right)\phi^{\prime}\left(\ln\left({ \frac{V_0}{D}}\right)\right)dt +\frac{\sigma^2}{2}\phi^{\prime\prime}\left(\ln\left({ \frac{V_0}{D}}\right)\right)dt \end{aligned} $$

where $\phi^{\prime\prime}(u)$ stands for $\frac{\partial^2\phi(u)}{\partial u^2}$.

If we substitute this into Eq. 24, ignore dt ² and divide both sides of the equation by dt, we obtain

$$ \frac{\sigma^2}{2}\phi^{\prime\prime}\left(\ln\left({ \frac{V_0}{D}}\right)\right)+\left(r-\frac{\sigma^2}{2}-\lambda\mu_J\right)\phi^{\prime} \left(\ln\left({\frac{V_0}{D}}\right)\right) =\lambda\phi\left(\ln\left({ \frac{V_0}{D}}\right)\right)-\lambda\int_{-\infty}^{\ln\left({ \frac{V_0}{D}}\right)}\phi\left(\ln\left({ \frac{V_0}{D}}\right)-x\right)dF(x). $$

(25)

Since $\phi\left(\ln\left({\frac{V_0}{D}}\right)\right)=1-\psi\left(\ln\left({ \frac{V_0}{D}}\right)\right)$, the integral-differential equation for $\psi\left(\ln\left({ \frac{V_0}{D}}\right)\right)$ is given by

$$ \begin{aligned} \frac{\sigma^2}{2}\psi^{\prime\prime}&\left(\ln\left({ \frac{V_0}{D}}\right)\right)+\left(r-\frac{\sigma^2}{2}-\lambda\mu_J\right)\psi^{\prime} \left(\ln\left({\frac{V_0}{D}}\right)\right)\\ &=\lambda\left[\psi\left(\ln\left({ \frac{V_0}{D}}\right)\right)-S_X\left(\ln\left({ \frac{V_0}{D}}\right)\right)\right]-\lambda\int_{-\infty}^{\ln\left({ \frac{V_0}{D}}\right)}\psi\left(\ln\left({ \frac{V_0}{D}}\right)-x\right)dF(x). \end{aligned} $$

If we integrate both side of Eq. 25 over $u=\ln\left({\frac{V_0}{D}}\right)$, we have

$$ \begin{aligned} \int_0^s&\frac{\sigma^2}{2}\phi^{\prime\prime}(u)du+( r-\frac{\sigma^2}{2}-\lambda\mu_J) \int_0^s\phi^{\prime}(u)du\\ &=\int_0^s\lambda\phi(u)du-\int_0^s\lambda\int_{-\infty}^{u} \phi(u-x)dF(x)du\\ &=\lambda\left[\int_0^s\phi(s-y)dy-\int_{-\infty}^s \int_{z=s}^0 \phi(s-y)p(y-z)dzdy\right]\\ &=\lambda\left[\int_0^s\phi(s-y)dy-\int_{-\infty}^s \phi(s-y)[P(y)-P(y-s)]dy\right]\\ &=\lambda\left[\int_0^s\phi(s-y)[1-P(y)]dy-\int_{-\infty}^0 \phi(s-y)P(y)dy+\int_{-\infty}^s \phi(s-y)P(y-s)]dy\right].\\ &=\lambda\left[\int_0^s\phi(s-y)[1-P(y)]dy-\int_{-\infty}^0 \phi(s-y)P(y)dy+\int_{-\infty}^{0} \phi(-y)P(y)]dy\right].\\ \end{aligned} $$

With the boundary condition ϕ(0) = 0, we have

$$ \begin{aligned} &\frac{\sigma^2}{2}\phi^{\prime}(s)+ (r-\frac{\sigma^2}{2}-\lambda\mu_J)\phi(s)\\ &=\frac{\sigma^2}{2}\phi^{\prime}(0) +\lambda\left[\int_0^s\phi(s-y)[1-P(y)]dy-\int_{-\infty}^0 [\phi(s-y)- \phi(-y)]P(y)dy\right], \end{aligned} $$

(26)

where s is finite.

As $s \rightarrow \infty$, we have

$$ \begin{aligned} r-\frac{\sigma^2}{2}-\lambda\mu_J=&\frac{\sigma^2}{2}\phi^{\prime}(0)+\lim_{s\rightarrow \infty}\lambda\left[\int_0^s\phi(s-y)dy-\int_{-\infty}^s \int_{z=s}^0 \phi(s-y)p(y-z)dzdy\right]\\ =&\frac{\sigma^2}{2}\phi^{\prime}(0)+\lambda\left[\int_0^{\infty}1dy-\int_{-\infty}^{\infty} \int_{\infty}^0 1p(y-z)dzdy\right]\\ =&\frac{\sigma^2}{2}\phi^{\prime}(0)+\lambda\left[\int_0^{\infty}1dy-\int_{-\infty}^{\infty} P(y)dy\right]\\ =&\frac{\sigma^2}{2}\phi^{\prime}(0)+\lambda\left[\int_0^{\infty}[1-P(y)]dy-\int_{-\infty}^{0} P(y)dy\right]\\ =&\frac{\sigma^2}{2}\phi^{\prime}(0)+\lambda\mu_X, \end{aligned} $$

or $\phi^{\prime}(0)=\frac{c-\lambda\mu_{X}}{\frac{\sigma^2}{2}}$. Since that $\theta=\frac{c-\lambda\mu_{X}}{c}$ and $\alpha=\frac{r-\frac{\sigma^2}{2}-\lambda\mu_J}{\sigma^2/2}$, the Eq. 26 can be rewritten as

$$ \begin{aligned} &\phi^{\prime}(s)+\alpha\phi(s)\\ &=\theta\alpha+\frac{2\lambda}{\sigma^2}\left[\int_0^s\phi(s-y)[1-P(y)]dy-\int_{-\infty}^0 [\phi(s-y)- \phi(-y)]P(y)dy\right]. \end{aligned} $$

This is a defective renewal equation when the jumps are possibly negative.