Evolution prediction from tomography

Prediction is very difficult, especially if it’s about the future.

– Niels Bohr.

The future ain’t what it used to be.

– Yogi Berra.

Abstract

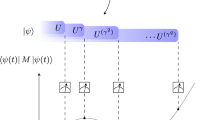
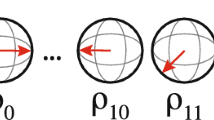
Quantum process tomography provides a means of measuring the evolution operator for a system at a fixed measurement time t. The problem of using that tomographic snapshot to predict the evolution operator at other times is generally ill-posed since there are, in general, infinitely many distinct and compatible solutions. We describe the prediction, in some “maximal ignorance” sense, of the evolution of a quantum system based on knowledge only of the evolution operator for finitely many times $0<\tau _{1}<\dots <\tau _{M}$ with $M\ge 1$. To resolve the ill-posedness problem, we construct this prediction as the result of an average over some unknown (and unknowable) variables. The resulting prediction provides a description of the observer’s state of knowledge of the system’s evolution at times away from the measurement times. Even if the original evolution is unitary, the predicted evolution is described by a non-unitary, completely positive map.

Appendices

Appendix 1: Schur–Weyl duality and analogs

In this section, we develop the group averaging results used in the proof of Theorem 1. These results may be related to the classic Schur–Weyl Duality.

Lemma 4

(Schur–Weyl duality) Let $\mathrm {U}^{\otimes n}(\mathcal {H})=\{U^{\otimes n} = U\otimes U\otimes \cdots \otimes U\;:\; U\in \mathrm {U}(\mathcal {H})\}\subset \mathrm {U}(\mathcal {H}^{\otimes n})$ and let $S_{n}\subset \mathrm {U}(\mathcal {H}^{\otimes n})$ be the n! element symmetric group represented as permutations of the n subsystems, i.e., $\pi \in S_{n}$ acts as $\pi (|\psi _{1}\rangle \otimes \cdots \otimes |\psi _{n}\rangle ) = |\psi _{\pi ^{-1}(1)}\rangle \otimes \cdots \otimes |\psi _{\pi ^{-1}(n)}\rangle$. Then the group algebras $\mathbb {C}\mathrm {U}^{\otimes n}(\mathcal {H})$ and $\mathbb {C}S_{n}$ are each the centralizer (i.e., commutant) of the other within ${\mathcal {B}}(\mathcal {H}^{\otimes n})$ [10,11,12,13].

For the results that follow, we want a very similar lemma, but on ${\mathcal {B}}(\mathcal {H})\simeq \mathcal {H}\otimes \mathcal {H}^{*}$, rather than on $\mathcal {H}\otimes \mathcal {H}$, namely:

Lemma 5

Let $\mathrm {PU}(\mathcal {H})=\{{{\mathrm{Ad}}}_{U}\;:\; U\in \mathrm {U}(\mathcal {H})\}\subset \mathrm {U}({\mathcal {B}}(\mathcal {H}))$ where for any $A\in {\mathcal {B}}(\mathcal {H})$ and $U\in \mathrm {U}(\mathcal {H})$, the adjoint action of U on A is given by ${{\mathrm{Ad}}}_{U}(A) = UAU^{\dag }$, and let $S_{2}\subset \mathrm {U}({\mathcal {B}}(\mathcal {H}))$ be the two element group comprising the identity map ${{\mathrm{id}}}$ and the trace-preserving operator $Q:A\mapsto \frac{2{{\mathrm{Tr}}}(A)}{\mathfrak {d}}\mathbbm {1}- A$ where $\mathfrak {d}= \dim (\mathcal {H})$ (it is easy to check that Q is a unitary involution, $Q^{*} = Q$ and $Q^{2} = {{\mathrm{id}}}$). Then the group algebras $\mathbb {C}\mathcal {\mathrm {PU}(\mathcal {H})}$ and $\mathbb {C}S_{2}$ are each the centralizer of the other within ${\mathcal {B}}\big ({\mathcal {B}}(\mathcal {H})\big )$, the algebra of all bounded complex-linear superoperators acting on ${\mathcal {B}}(\mathcal {H})$.

Proof

First, consider an $X\in {\mathcal {B}}\big ({\mathcal {B}}(\mathcal {H})\big )$ that commutes with all ${{\mathrm{Ad}}}_{U}\in \mathrm {PU}(\mathcal {H})$. Then for any $A\in {\mathcal {B}}(\mathcal {H})$, and any $\Omega \in \mathrm {U}(\mathcal {H})$ such that $\Omega A \Omega ^{\dag } = A$, $X(A) = X(\Omega A \Omega ^{\dag }) = \Omega X(A)\Omega ^{\dag }$, so that X(A) commutes with all unitary operators that commute with A. Since ${{\mathrm{Comm}}}(A)$ is the complex-linear span of the unitary stabilizer ${{\mathrm{Stab}}}_{\mathrm {U}(\mathcal {H})}(A)$, this implies that X(A) commutes with every operator in ${{\mathrm{Comm}}}(A)$, and therefore $X(A)\in {{\mathrm{Bicomm}}}(A)$. Furthermore, $X\big (| 1 \rangle \! \langle 1 |\big )\in {{\mathrm{Bicomm}}}\big (| 1 \rangle \! \langle 1 |\big )$ implies that $X\big (| 1 \rangle \! \langle 1 |\big ) = a| 1 \rangle \! \langle 1 | + b\mathbbm {1}$ for some coefficients $a,b\in \mathbb {C}$. Since for any $i=1,\dots , \mathfrak {d}$, there exists a permutation matrix $\pi \in S_{\mathfrak {d}}\subset \mathrm {U}(\mathcal {H})$ such that $\pi |1\rangle = |i\rangle$, it follows that

$$\begin{aligned} X(| i \rangle \! \langle i |) = X(\pi | 1 \rangle \! \langle 1 |\pi ^{\dag }) = \pi X(| 1 \rangle \! \langle 1 |)\pi ^{\dag } = a| i \rangle \! \langle i | + b\mathbbm {1}. \end{aligned}$$

(19)

By complex linearity, any diagonal matrix D transforms as

$$\begin{aligned} X(D) = \sum _{i}D_{ii}X(| i \rangle \! \langle i |) = a\sum _{i}D_{ii}| i \rangle \! \langle i | + b\sum _{i}D_{ii}\mathbbm {1}= aD + b{{\mathrm{Tr}}}(D)\mathbbm {1}. \end{aligned}$$

(20)

Since any normal operator $A\in {\mathcal {B}}(\mathcal {H})$ is unitarily diagonalizable as $A = \Omega D \Omega ^{\dag }$ for some $\Omega \in \mathrm {U}(\mathcal {H})$ and diagonal D, it follows that X acts on normal operators as

$$\begin{aligned} X(A) = X(\Omega D \Omega ^{\dag }) = \Omega X(D)\Omega ^{\dag } = \Omega \big [aD + b{{\mathrm{Tr}}}(D)\mathbbm {1}\big ]\Omega ^{\dag } = aA + b{{\mathrm{Tr}}}(A)\mathbbm {1}. \end{aligned}$$

(21)

Finally, since ${\mathcal {B}}(\mathcal {H})$ is spanned by the normal operators, complex linearity implies that X must act as $X(A) = aA + b{{\mathrm{Tr}}}(A)\mathbbm {1}$ on all operators $A\in {\mathcal {B}}(\mathcal {H})$, so X is an element of the complex span of the identity superoperator ${{\mathrm{id}}}$ and the map $A\mapsto {{\mathrm{Tr}}}(A)\mathbbm {1}$, which is identical to the complex span of ${{\mathrm{id}}}$ and the map $Q:A\mapsto \frac{2{{\mathrm{Tr}}}(A)}{\mathfrak {d}}\mathbbm {1}- A$. Since ${{\mathrm{id}}}$ and Q both trivially commute with all ${{\mathrm{Ad}}}_{U}\in \mathrm {PU}(\mathcal {H})$, defining $S_{2}:=\{{{\mathrm{id}}}, Q\}$, we get that $\mathbb {C}S_{2}$ is the centralizer (i.e., commutant) of $\mathbb {C}\mathrm {PU}(\mathcal {H})$.

That $\mathbb {C}\mathrm {PU}(\mathcal {H})$ is the centralizer of $\mathbb {C}S_{2}$ can now be seen as a consequence of either the Schur double centralizer theorem [13, 14] or the von Neumann double commutant theorem [15, 16]. $\square$

Remark 3

Let $Q_{\pm } := \frac{{{\mathrm{id}}}\pm Q}{2}$ be the projectors onto the $\pm 1$ eigenspaces of Q. Then $Q_{+}(A) = \frac{{{\mathrm{Tr}}}(A)}{\mathfrak {d}}\mathbbm {1}$ and $Q_{-}(A) = A - \frac{{{\mathrm{Tr}}}(A)}{\mathfrak {d}}\mathbbm {1}$. So the eigenspaces of Q are the 1-dimensional space spanned by identity $\mathbb {C}\mathbbm {1}= \{a\mathbbm {1}\;:\;a\in \mathbb {C}\}$ and the $(\mathfrak {d}^{2}-1)$-dimensional space of trace zero operators, i.e., $\mathrm {sl}(\mathcal {H})$.

Lemma 6

For any $B\in {\mathcal {B}}(\mathcal {H})$, let ${{\mathrm{Ad}}}_{B}\in {\mathcal {B}}\big ({\mathcal {B}}(\mathcal {H})\big )$ denote the adjoint operator ${{\mathrm{Ad}}}_{B}(A) = BAB^{\dag }$ and define the group average

$$\begin{aligned} \overline{{{\mathrm{Ad}}}_{B}} := \int _{W\in \mathrm {U}(\mathcal {H})}\mathrm {d}\eta (W) {{\mathrm{Ad}}}_{W} \circ {{\mathrm{Ad}}}_{B}\circ {{\mathrm{Ad}}}_{W}^{*} = \int _{W\in \mathrm {U}(\mathcal {H})}\mathrm {d}\eta (W) {{\mathrm{Ad}}}_{WBW^{\dag }}, \end{aligned}$$

(22a)

in other words, $\overline{{{\mathrm{Ad}}}_{B}}$ acts on an arbitrary $A\in {\mathcal {B}}(\mathcal {H})$ as

$$\begin{aligned} \overline{{{\mathrm{Ad}}}_{B}}(A) = \int _{W\in \mathrm {U}(\mathcal {H})}\mathrm {d}\eta (W)WBW^{\dag } AWB^{\dag }W^{\dag }, \end{aligned}$$

(22b)

where $\eta$ is the normalized Haar measure. Then $\overline{{{\mathrm{Ad}}}_{B}}$ is given by the map

$$\begin{aligned} \overline{{{\mathrm{Ad}}}_{B}}(A) = \frac{\mathfrak {d}|{{\mathrm{Tr}}}(B)|^{2} - \Vert B\Vert _{\mathrm {HS}}^{2}}{\mathfrak {d}(\mathfrak {d}^{2}-1)}A + \frac{\mathfrak {d}\Vert B\Vert _{\mathrm {HS}}^{2} - |{{\mathrm{Tr}}}(B)|^{2}}{\mathfrak {d}^{2} -1}\frac{{{\mathrm{Tr}}}(A)}{\mathfrak {d}}\mathbbm {1}\end{aligned}$$

(23)

where $\mathfrak {d}=\dim (\mathcal {H})$, and when $\mathfrak {d}=1$, this is simply $\overline{{{\mathrm{Ad}}}_{B}}(A) = |B|^{2}A$. For $X\in \mathrm {U}(\mathcal {H})$, this becomes

$$\begin{aligned} \overline{{{\mathrm{Ad}}}_{X}}(A) = \frac{|{{\mathrm{Tr}}}(X)|^{2} - 1}{\mathfrak {d}^{2}-1}A + \frac{\mathfrak {d}^{2} - |{{\mathrm{Tr}}}(X)|^{2}}{\mathfrak {d}^{2}-1}\frac{{{\mathrm{Tr}}}(A)}{\mathfrak {d}}\mathbbm {1}. \end{aligned}$$

(24)

Proof

Because of the invariance of the Haar measure, $\overline{{{\mathrm{Ad}}}_{B}}$ is readily seen to be the orthogonal projection of ${{\mathrm{Ad}}}_{B}$ into the centralizer of $\mathrm {PU}(\mathcal {H})= \{{{\mathrm{Ad}}}_{W}\;:\;W\in \mathrm {U}(\mathcal {H})\}$, which, by Lemma 5, is $\mathbb {C}S_{2} = {{\mathrm{Span}}}_{\mathbb {C}}\{{{\mathrm{id}}}, Q\}$. In other words,

$$\begin{aligned} \overline{{{\mathrm{Ad}}}_{B}}&= \frac{\langle {{\mathrm{id}}}, {{\mathrm{Ad}}}_{B}\rangle }{\langle {{\mathrm{id}}}, {{\mathrm{id}}}\rangle }{{\mathrm{id}}}+ \frac{\langle {\tilde{Q}}, {{\mathrm{Ad}}}_{B}\rangle }{\langle {\tilde{Q}}, {\tilde{Q}}\rangle }{\tilde{Q}} \end{aligned}$$

(25)

where ${\tilde{Q}} := Q-\frac{\langle Q,{{\mathrm{id}}}\rangle }{\langle {{\mathrm{id}}}, {{\mathrm{id}}}\rangle }{{\mathrm{id}}}$ is the component of Q orthogonal to ${{\mathrm{id}}}$. It remains simply to compute the inner products, which can be computed using an orthonormal basis $\{|j\rangle \}$ for $\mathcal {H}$ as $\langle X, Y\rangle = {{\mathrm{Tr}}}(X^{*}\circ Y) = \sum _{j,k}\big \langle | j \rangle \! \langle k |, X^{*}\circ Y\big (| j \rangle \! \langle k |\big )\big \rangle = \sum _{j,k}\big \langle X\big (| j \rangle \! \langle k |\big ), Y\big (| j \rangle \! \langle k |\big )\big \rangle$. So, first of all,

$$\begin{aligned} \langle {{\mathrm{id}}}, {{\mathrm{id}}}\rangle&= \sum _{j,k}\big \langle | j \rangle \! \langle k |, | j \rangle \! \langle k |\big \rangle = \mathfrak {d}^{2} \end{aligned}$$

(26a)

$$\begin{aligned} \langle Q, {{\mathrm{id}}}\rangle&= \sum _{j,k}\big \langle Q(| j \rangle \! \langle k |), | j \rangle \! \langle k |\big \rangle = \sum _{j\ne k}\big \langle -| j \rangle \! \langle k |, | j \rangle \! \langle k |\big \rangle \nonumber \\&\quad + \sum _{j}\left\langle \frac{2}{\mu _{i}} \mathbbm {1}_{V_{i}} - | j \rangle \! \langle j |, | j \rangle \! \langle j |\right\rangle \nonumber \\&= \big (\mathfrak {d}-\mathfrak {d}^{2}\big ) + (2-\mathfrak {d}) = 2-\mathfrak {d}^{2}, \end{aligned}$$

(26b)

so that ${\tilde{Q}}(A) = \frac{2{{\mathrm{Tr}}}(A)}{\mathfrak {d}}\mathbbm {1}- \frac{2}{\mathfrak {d}}A$. Now,

$$\begin{aligned} \langle {{\mathrm{id}}}, {{\mathrm{Ad}}}_{B}\rangle&= \sum _{j,k}\big \langle | j \rangle \! \langle k |, B| j \rangle \! \langle k |B^{\dag }\big \rangle = \sum _{j,k}\left\langle j \right| B\left| j \right\rangle \left\langle k \right| B^{\dag }\left| k \right\rangle = |{{\mathrm{Tr}}}(B)|^{2} \end{aligned}$$

(27a)

$$\begin{aligned} \langle {\tilde{Q}}, {{\mathrm{Ad}}}_{B}\rangle&= \sum _{j,k}\big \langle \frac{2{{\mathrm{Tr}}}(| j \rangle \! \langle k |)}{\mathfrak {d}}\mathbbm {1}- \frac{2}{\mathfrak {d}^{2}}| j \rangle \! \langle k |, B| j \rangle \! \langle k |B^{\dag }\big \rangle = \frac{2}{\mathfrak {d}}\sum _{j}{{\mathrm{Tr}}}(B| j \rangle \! \langle j |B^{\dag })\nonumber \\&\quad - \frac{2}{\mathfrak {d}^{2}}\sum _{j,k}\left\langle j \right| B\left| j \right\rangle \left\langle k \right| B^{\dag }\left| k \right\rangle \nonumber \\&= \frac{2}{\mathfrak {d}}\Vert B\Vert _{\mathrm {HS}}^{2} - \frac{2}{\mathfrak {d}^{2}}|{{\mathrm{Tr}}}(B)|^{2} = \frac{2}{\mathfrak {d}^{2}}\Big (\mathfrak {d}\Vert B\Vert _{\mathrm {HS}}^{2} - |{{\mathrm{Tr}}}(B)|^{2}\Big )\end{aligned}$$

(27b)

$$\begin{aligned} \langle {\tilde{Q}}, {\tilde{Q}}\rangle&= \sum _{j,k}\big \langle {\tilde{Q}}(| j \rangle \! \langle k |), {\tilde{Q}}(| j \rangle \! \langle k |)\big \rangle = \frac{4}{\mathfrak {d}^{4}}\sum _{j\ne k}\big \langle | j \rangle \! \langle k |, | j \rangle \! \langle k |\big \rangle \nonumber \\&\quad + \sum _{j}\left\langle \frac{2}{\mathfrak {d}}\mathbbm {1}- \frac{2}{\mathfrak {d}^{2}}| j \rangle \! \langle j |, \frac{2}{\mathfrak {d}}\mathbbm {1}- \frac{2}{\mathfrak {d}^{2}}| j \rangle \! \langle j |\right\rangle \nonumber \\&= \frac{4(\mathfrak {d}-1)}{\mathfrak {d}^{3}} + 4 - \frac{8}{\mathfrak {d}^{2}} + \frac{4}{\mathfrak {d}^{3}} = 4\left( 1-\frac{1}{\mathfrak {d}^{2}}\right) , \end{aligned}$$

(27c)

whence,

$$\begin{aligned} \overline{{{\mathrm{Ad}}}_{B}}&= \frac{\langle {{\mathrm{id}}}, {{\mathrm{Ad}}}_{B}\rangle }{\langle {{\mathrm{id}}}, {{\mathrm{id}}}\rangle }{{\mathrm{id}}}+ \frac{\langle {\tilde{Q}}, {{\mathrm{Ad}}}_{B}\rangle }{\langle {\tilde{Q}}, {\tilde{Q}}\rangle }{\tilde{Q}} = \frac{|{{\mathrm{Tr}}}(B)|^{2}}{\mathfrak {d}}{{\mathrm{id}}}+ \frac{\mathfrak {d}\Vert B\Vert _{\mathrm {HS}}^{2} - |{{\mathrm{Tr}}}(B)|^{2}}{\mathfrak {d}^{2}-1}{\tilde{Q}}\end{aligned}$$

(28a)

$$\begin{aligned} \overline{{{\mathrm{Ad}}}_{B}}(A)&= \frac{\mathfrak {d}|{{\mathrm{Tr}}}(B)|^{2} - \Vert B\Vert _{\mathrm {HS}}^{2}}{\mathfrak {d}(\mathfrak {d}^{2}-1)}A + \frac{\mathfrak {d}\Vert B\Vert _{\mathrm {HS}}^{2} - |{{\mathrm{Tr}}}(B)|^{2}}{\mathfrak {d}^{2}-1}\frac{{{\mathrm{Tr}}}(A)}{\mathfrak {d}}\mathbbm {1}. \end{aligned}$$

(28b)

$\square$

Lemma 7

Let $\mathcal {H}= \bigoplus _{i=1}^{\kappa }V_{i}$ be an orthogonal decomposition and $\mu _{i} = \dim (V_{i})$. For any $B = \bigoplus _{i=1}^{\kappa } B_{i}$ with $B_{i}\in {\mathcal {B}}(V_{i})$, define the group average

$$\begin{aligned} \overline{{{\mathrm{Ad}}}_{B}}^{\bigoplus }:=\int _{R\in \bigoplus _{i=1}^{\kappa } \mathrm {U}(V_{i})}\mathrm {d}\eta (R) \; {{\mathrm{Ad}}}_{R}\circ {{\mathrm{Ad}}}_{B} \circ {{\mathrm{Ad}}}_{R}, \end{aligned}$$

(29)

in other words, for any $A\in {\mathcal {B}}(\mathcal {H})$,

$$\begin{aligned} \overline{{{\mathrm{Ad}}}_{B}}^{\bigoplus }(A) = \int _{R\in \bigoplus _{i=1}^{\kappa }\mathrm {U}(V_{i})}\mathrm {d}\eta (R) \; RBR^{\dag }ARB^{\dag }R^{\dag }. \end{aligned}$$

(30)

Then

$$\begin{aligned} \overline{{{\mathrm{Ad}}}_{B}}^{\bigoplus }(A)&= \bigoplus _{i=1}^{\kappa } \frac{\mu _{i}|{{\mathrm{Tr}}}(B_{i})|^{2} - \Vert B_{i}\Vert _{\mathrm {HS}}^{2}}{\mu _{i}(\mu _{i}^{2}-1)}A_{(ii)} + \frac{\mu _{i}\Vert B\Vert _{\mathrm {HS}}^{2} - |{{\mathrm{Tr}}}(B)|^{2}}{\mu _{i}^{2}-1}\frac{{{\mathrm{Tr}}}(A_{(ii)})}{\mu _{i}}\mathbbm {1}_{V_{i}}\nonumber \\&\oplus \bigoplus _{i\ne j=1}^{\kappa } \frac{{{\mathrm{Tr}}}(B_{i})\overline{{{\mathrm{Tr}}}(B_{j})}}{\mu _{i}\mu _{j}}A_{(ij)}. \end{aligned}$$

(31a)

Proof

First, observe that

$$\begin{aligned} \overline{{{\mathrm{Ad}}}_{B}}^{\bigoplus }(A)= & {} \bigoplus _{i=1}^{\kappa }\overline{{{\mathrm{Ad}}}_{B_{i}}}(A_{(ii)}) \oplus \bigoplus _{i\ne j=1}^{\kappa } \int _{R_{i}\in \mathrm {U}(V_{i})}\mathrm {d}\eta (R_{i})\nonumber \\&\times \int _{R_{j}\in \mathrm {U}(V_{j})}\mathrm {d}\eta (R_{j}) \; R_{i}B_{i}R_{i}^{\dag }A_{(ij)}R_{j}B_{j}^{\dag }R_{j}^{\dag } \end{aligned}$$

(32)

where $\overline{{{\mathrm{Ad}}}_{B_{i}}}$ is as defined in Lemma 6. The proof is then completed by invoking Lemma 6 and by observing that under normalized Haar measure,

$$\begin{aligned} \int _{R_{i}\in \mathrm {U}(V_{i})}\mathrm {d}\eta (R_{i}) \; R_{i}B_{i}R_{i}^{\dag } = \frac{{{\mathrm{Tr}}}(B)}{\mu _{i}}\mathbbm {1}_{V_{i}}. \end{aligned}$$

(33)

$\square$

Appendix 2: Characteristic functions of distributions on ${\mathbb {Z}}$

Fig. 1

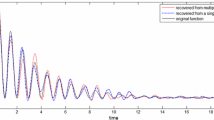
Plots of the squared characteristic functions $|\varphi _{\mathbb {P}}(t)|^{2}$ for several probability distributions $\mathbb {P}(k)$ on ${\mathbb {Z}}$. In left-to-right, top-to-bottom order, they are the characteristic functions for: a the exponential distribution, b the truncated uniform distribution, c the semicircular distribution, d the Cauchy–Lorentz distribution, e the binomial distribution, and f the normal distribution

Table 1 Some common probability distributions on ${\mathbb {Z}}$ and the associated characteristic functions

We take a look at the characteristic functions for several common distributions on ${\mathbb {Z}}$. The squared characteristic functions are plotted in Figure 1. All of the distribution families in Table 1 span the range from the Kronecker delta at $k=0$ (the characteristic function of which is the constant function $\varphi _{\mathbb {P}}(t) = 1$) to the untruncated uniform distribution on ${\mathbb {Z}}$ (with characteristic function the discontinuous function which is zero everywhere except at integer multiples of $2\pi$, where it takes the value 1). As all of these distributions are symmetric unimodal distributions centered at $k=0$, they all have broadly similar characteristic functions. It may be noticed, however, that the characteristic function of the Cauchy–Lorentz distribution has cusps at integer multiples of $2\pi$, which is related to the fact that the higher even moments $\mathbb {E}[k^{2q}] = \sum _{k}k^{2q}\mathbb {P}(k)$ do not converge for $q\ge 1$.