Tuning linear and nonlinear characteristics of a resonator via nonlinear interaction with a secondary resonator

Abstract

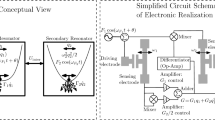
We conside the dynamics of a nonlinear resonator that is nonlinearly coupled to a linear resonator that has a relatively short decay time. In this case, the secondary (linear) resonator adiabatically tracks the primary (nonlinear) resonator. This model, which is motivated by ongoing experimental work in nano-resonators, is analyzed analytically and numerically to show that the linear and nonlinear characteristics of the primary resonator can be altered in a significant manner by the coupling to the secondary resonator. Such an arrangement may provide a practical means of tuning resonator characteristics in applications.

Appendix A: Brief discerption of the microscopic theory of a resonator that interacts with a medium

We consider the total Hamiltonian of a nonlinear resonator with a potential U(x) that is coupled to a medium of harmonic oscillators. The analysis is well-known [16, 19, 31, 32, 43,44,45,46]; here, we briefly outline it for completeness. The total Hamiltonian includes the resonator Hamiltonian $\mathcal {H}_r$, the medium Hamiltonian $\mathcal {H}_m$, and the interaction Hamiltonian $\mathcal {H}_\mathrm{inter}$ and reads

$$\begin{aligned} \mathcal {H}=\frac{v^2}{2}+U(x)+\frac{1}{2}\sum _k(p_k^2+\omega _k^2q_k^2)-G(x)\sum _k\epsilon _kq_k. \end{aligned}$$

(25)

The equations of motion resulting from Eq. (25) are

$$\begin{aligned} \ddot{x}&=-U'(x)+G'(x)\sum _k\epsilon _kq_k, \end{aligned}$$

(26)

$$\begin{aligned} \ddot{q}_k&=-\omega _k^2q_k+\epsilon _kG(x). \end{aligned}$$

(27)

We formally solve Eq. (27) in terms of its Green’s function, i.e.,

$$\begin{aligned} q_k(t)&=q_k(0)\cos (\omega _{k}t)+\frac{p_k(0)}{\omega _{k}}\sin (\omega _{k}t) \nonumber \\&+\frac{\epsilon _k}{\omega _{k}}\int _0^tG(x(\tau ))\sin (\omega _{k}(t-\tau ))\mathrm{d}\tau . \end{aligned}$$

(28)

Upon inserting Eq. (28) into Eq. (26), we find that

$$\begin{aligned} \ddot{x}=-U'(x)+G'(x)(L[x]+F), \end{aligned}$$

(29)

where

$$\begin{aligned} L[x]=&\sum _k\frac{\epsilon _k^{2}}{\omega _{k}}\int _0^tG(x(\tau ))\sin (\omega _{k}(t-\tau ))\mathrm{d}\tau , \end{aligned}$$

(30)

$$\begin{aligned} F(t)=&\sum _k\epsilon _k\left[ q_k(0)\cos (\omega _{k}t)+\frac{p_k(0)}{\omega _{k}}\sin (\omega _{k}t)\right] . \end{aligned}$$

(31)

Using integration by parts, we can rewrite Eq. (30) as

$$\begin{aligned} L[x]=&-G(x(t))\sum _k\frac{\epsilon _k^{2}}{\omega _{k}^2}+G(x(0))\sum _k\frac{\epsilon _k^{2}}{\omega _{k}^2}\cos (\omega _{k}t)\nonumber \\&-\sum _k\frac{\epsilon _k^{2}}{\omega _{k}^2}\int _0^t\dot{x}(\tau )G'(x(\tau ))\cos (\omega _{k}(t-\tau ))\mathrm{d}\tau . \end{aligned}$$

(32)

We assume that the medium contains an infinite number of harmonic oscillators with a continuous spectrum. Consequently, we approximate the sum over k as an integral. Toward this end, we define the spectral density of the bath as $g(\omega )\mathrm{d}\omega =\sum _{\omega<\omega _k<\omega +\mathrm{d}\omega }\epsilon _k^{2}/\omega _{k}^2$.

Using Eq. (32) along with the assumption of a continuous spectrum of the medium, we rewrite Eq. (29) as

$$\begin{aligned}&\ddot{x}+G'(x)\int _0^t\varGamma (t-\tau )\dot{x}(\tau )G'(x(\tau ))\mathrm{d}\tau \nonumber \\&\quad +V_\mathrm{ren}'(x)=G'(x)\tilde{F}, \end{aligned}$$

(33)

where $\varGamma (t-\tau )=\int _{-\infty }^{\infty }g(\omega )\cos (\omega (t-\tau ))\mathrm{d}\omega$ is the memory of the friction, $V_\mathrm{ren}(x)=U(x)+\frac{1}{2}G^2(x)\int _{-\infty }^{\infty }g(\omega )\mathrm{d}\omega$ is the renormalized potential of the resonator, and $\tilde{F}=F+G(x(0))\int _{-\infty }^{\infty }g(\omega )\cos (\omega t)\mathrm{d}\omega$ is a noise term.

The statistical properties of the noise term F are determined as follows: We assume that at $t=0$, the interaction between the bath and the resonator is turned on and considers an ensemble of initial states in which x(0) is held fixed but the initial bath variables $q_k(0),p_k(0)$ are drawn at random from a canonical distribution characterized by a temperature T, i.e.,

$$\begin{aligned} \mathcal {P}(\{q_k,p_k\}|x(0)=x)\propto \mathrm{e}^{-\mathcal {H}_m/k_BT}. \end{aligned}$$

(34)

With this conditional probability for the bath variables, the noise term F obeys the fluctuation–dissipation relations

$$\begin{aligned} \langle F\rangle _{\mathcal {P}}=0,~\langle F(t) F(\tau )\rangle _{\mathcal {P}}=k_BT\varGamma (t-\tau ), \end{aligned}$$

(35)

and hence, it is a colored Gaussian noise. Note that for a flat spectrum of the bath weighted with the coupling (the so-called Ohmic dissipation), we can use the Markovian approximation, where $\varGamma (t-\tau )=2\langle g\rangle \delta (t-\tau )$ and $\langle g\rangle /\pi$ is the averaged value of the spectrum. Hence, Eq. (33) reduces to

$$\begin{aligned} \ddot{x}+2\langle g\rangle G'^2(x)\dot{x}+V_\mathrm{ren}'(x)=G'(x) F, \end{aligned}$$

(36)

and F becomes a white Gaussian noise.

Comparison between Eqs. (14) and (36) reveals that, for both cases of discrete and continuous spectrum baths, the linear coupling is the source of the induced linear damping and the shift in the eigenfrequency of the resonator, and the nonlinear coupling leads to nonlinear damping and modifications in the nonlinear conservative terms of the resonator. However, for the case of a continuous spectrum bath there are also fluctuating back-action terms that come along with the damping terms and balance them, i.e., the linear damping is associated with an additive noise term $2\langle g\rangle G'^2(0)\dot{x}\longleftrightarrow G'(0)\tilde{F}$ and the nonlinear damping with a multiplicative noise $2\langle g\rangle [G'^2(x)-G'^2(0)]\dot{x}\longleftrightarrow [G'(x)-G'(0)]\tilde{F}$.