Study of Newton’s cradle using a new discrete approach

Abstract

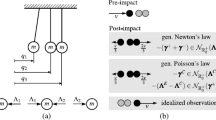
This paper presents a new discrete approach for treating simultaneous, multiple point, indeterminate impact. The proposed approach uses rigid body constraints to address the indeterminacy in the equations of motion with respect to impact forces. The post-collision velocities are determined by exploiting the work–energy relationship and using an energetic coefficient of restitution to model energy dissipation. A new global, or system level, interpretation of the energetic coefficient of restitution is used to resolve the post-collision velocities. An interesting phenomenon observed herein is that a single collision may involve multiple impact events. The well-known example of Newton’s cradle is studied in this work to demonstrate the application of the proposed approach. Simulations are conducted using a three- and five-ball system with different energetic coefficients of restitution for uniform and non-uniform series of spheres. The results obtained in this work are compared to theoretical and experimental results reported in other works.

Appendices

Appendix A: Supplemental data and analysis plots

Table 4 Model and simulation parameters: L is the length that each ball hangs from (measured to mass center), R is the radius of each ball, and λ is the horizontal distance between each ball’s mass centers. In this work, λ=2R (no separation) and all balls at rest are in contact. The terms m _i are the mass of each ball i, $v_{1}^{-}$ is the initial velocity of Ball A when it collides with the chain of balls initially at rest, and μ _i is the coefficient of friction between balls i and i+1

Fig. 16

Case I: (a) Generalized speeds for a three-ball Newton’s cradle, and (b) energy consistency throughout simulation with e _∗=1

Fig. 17

Case II: (a) Generalized speeds for a three-ball Newton’s cradle, and (b) energy consistency throughout simulation with e _∗=0.85

Fig. 18

Case III: (a) Generalized speeds for a five-ball Newton’s cradle, and (b) energy consistency throughout simulation with e _∗=1

Fig. 19

Case IV: (a) Generalized speeds for a five-ball Newton’s cradle, and (b) energy consistency throughout simulation with e _∗=0.8

Fig. 20

Case V: (a) Generalized speeds for a non-uniform series, five-ball Newton’s cradle, and (b) energy consistency throughout simulation

Appendix B: Derivation of constraints

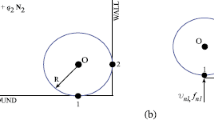
Here, the general form of the velocity constraint is derived based on the theory of rigid body dynamics to address the indeterminacy in (1), as in [16]. The developments given below are for Ball B shown in Fig. 1b. If the mass center of Ball B is point O, then the velocity at this point is known, v _O , with respect to the world frame established in Fig. 1a, such that the velocity of points B1 and B2 shown in Fig. 1b are found as

$$ \begin{array}{lcl} \boldsymbol{v}_{B1} & = & \boldsymbol{v}_O + \boldsymbol{v}_{\mathrm{OB}1} = \boldsymbol{v}_O + \boldsymbol{\omega} \times\mathbf{P}_{\mathrm{OB}1}, \\ \boldsymbol{v}_{B2} & = & \boldsymbol{v}_O + \boldsymbol{v}_{\mathrm{OB}2} = \boldsymbol{v}_O + \boldsymbol{\omega} \times\mathbf{P}_{\mathrm{OB}2}, \\ \end{array} $$

(29)

where v _OB1 is the relative velocity between points O and B1 and v _OB2 is the relative velocity between points O and B2 [17]. Eliminating v _O from the relations in (29) yields

$$ \boldsymbol{v}_{B1} - \boldsymbol{v}_{B2} = \boldsymbol{\omega} \times(\mathbf{P}_{\mathrm{OB}1} - \mathbf{P}_{\mathrm{OB}2}). $$

(30)

If the dot product of the unit direction between impact points B1 and B2 is applied to each side, then

$$ (\boldsymbol{v}_{B1} - \boldsymbol{v}_{B2}) \cdot\frac{(\mathbf{P}_{\mathrm{OB}1} - \mathbf{P}_{\mathrm{OB}2})}{|(\mathbf{P}_{\mathrm{OB}1} - \mathbf{P}_{\mathrm{OB}2})|} = \boldsymbol{\omega} \times(\mathbf{P}_{\mathrm{OB}1} - \mathbf{P}_{\mathrm{OB}2}) \cdot\frac{(\mathbf{P}_{\mathrm{OB}1} - \mathbf {P}_{\mathrm{OB}2})}{|(\mathbf{P}_{\mathrm{OB}1} - \mathbf{P}_{\mathrm{OB}2})|} $$

(31)

such that the right-hand side of (31) is zero and the rigid body constraint is expressed as

$$ (\boldsymbol{v}_{B1} - \boldsymbol{v}_{B2}) \cdot \frac{(\mathbf{P}_{\mathrm{OB}1} - \mathbf{P}_{\mathrm{OB}2})}{|(\mathbf{P}_{\mathrm{OB}1} - \mathbf{P}_{\mathrm{OB}2})|} = 0. $$

(32)

Evaluating the terms involved in this constraint yields

$$ \bigl( (v_4 - v_6) \mathbf{N}_1 + (v_3 - v_5) \mathbf{N}_2 \bigr) \cdot(- \mathbf{N}_2) = v_5 - v_3 = 0. $$

(33)

What effect does this velocity constraint have on the force space? It is necessary to examine the dual nature of the velocity and force constraint spaces. Consider

$$ \boldsymbol{\vartheta} = \left[ \begin{array}{c} v_1 \\ v_2 \\ v_{3} \\ v_{4} \\ v_{5} \\ v_{6} \\ v_7 \\ v_8 \end{array} \right] = \left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} v_1 \\ v_2 \\ v_{3} \\ v_{4} \\ v_{6} \\ v_7 \\ v_8 \end{array} \right] = Q \boldsymbol{\vartheta}^{*} $$

(34)

where the term v ₅ is constrained, without any loss of generality. Taking the left-inverse of Q yields

$$ \boldsymbol{\vartheta}^{*} = \bigl( Q^T Q \bigr)^{-1} Q^T \boldsymbol{\vartheta} = Q^+ \boldsymbol{\vartheta}. $$

(35)

The dual nature of the Jacobian also defines a relationship between dependent and independent forces:

$$ \boldsymbol{\varGamma} = J^T \mathbf{F} = J^T \bigl( Q^+ \bigr)^T \mathbf{F}^{*} $$

(36)

which yields

$$ \mathbf{F} = \bigl( Q^+ \bigr)^T \mathbf{F}^{*} \quad{\mbox{or}} \quad Q^T \mathbf{F} = \mathbf{F}^{*}. $$

(37)

The second expression in (37) is used to solve for F ^∗ as

$$ \mathbf{F}^{*} = Q^T \mathbf{F} = \left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad }c@{\quad}c} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} f_1 \\ f_2 \\ f_3 \\ f_4 \\ f_5 \\ f_6 \\ f_7 \\ f_8 \end{array} \right] = \left[ \begin{array}{c} f_1 \\ f_2 \\ f_3 + f_5 \\ f_4 \\ f_6 \\ f_7 \\ f_8 \end{array} \right]. $$

(38)

Substituting (38) back into the first relation in (37) reveals the constraint imposed on the forces as

$$\begin{aligned} \left[ \begin{array}{c} f_1 \\ f_2 \\ f_3 \\ f_4 \\ f_5 \\ f_6 \\ f_7 \\ f_8 \end{array} \right] =& \mathbf{F} = \bigl( Q^+ \bigr)^T \mathbf{F}^{*} = \left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0.5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0.5 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} f_1 \\ f_2 \\ f_3 + f_5 \\ f_4 \\ f_6 \\ f_7 \\ f_8 \end{array} \right] \\ =& \left[ \begin{array}{c} f_1 \\ f_2 \\ 0.5 (f_3 + f_5) \\ f_4 \\ 0.5 (f_3 + f_5) \\ f_6 \\ f_7 \\ f_8 \end{array} \right]. \end{aligned}$$

(39)

The third and fifth relations in (39) both yield

$$ 0 = f_3 - f_5 $$

(40)

which is used in Sect. 2.1 to eliminate the dependent force in the three-ball cases, see (4). Note that this process essentially can be stated as

$$ \mathbf{F} = \bigl( Q^+ \bigr)^T Q^T \mathbf{F}, $$

(41)

noting that the matrix (Q ⁺)^T Q ^T does not equal the identity matrix. This matrix projects F on the right-hand side of (41) into the space orthogonal to the velocity constraint, which must equal the original F. Technically, any vector of forces in the null space of (Q ⁺)^T Q ^T can be added to the right-hand side and still satisfy (41). However, the development of this solution was based on the existence of left-inverses which only find a single solution. In addition, it is expected that adding constraints to a problem would select a particular single solution. Whether or not multiple solutions exist within the proposed scheme will not be examined here, but will be investigated in future work.

Similarly, force constraints for Balls C and D in the five-ball cases can be determined:

$$\begin{aligned} 0 =& f_7 - f_9, \end{aligned}$$

(42)

$$\begin{aligned} 0 =& f_{11} - f_{13}. \end{aligned}$$

(43)

By using Newton’s third law and constraint equations (40), (42) in (43), a force constraint between Balls B, C and Balls B–D can be expressed as

$$\begin{aligned} 0 =& f_7 - f_9 = -f_5 - f_9 = -f_3 - f_9, \end{aligned}$$

(44)

$$\begin{aligned} 0 =& f_{11} - f_{13} = -f_{9} - f_{13} = -f_7 - f_{13} = f_5 - f_{13} = f_3 - f_{13}. \end{aligned}$$

(45)

The force constraints (44) and (45) can be applied to a four- and five-ball Newton cradle system, respectively, in the simultaneous, multiple point collision.