Stochastic Cooperative Communications Using a Geometrical Probability Approach for Wireless Networks

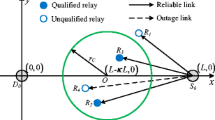
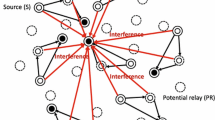
Abstract

In cooperative communications, signals are relayed to increase transmission range and user throughput. However, selection and coordination of relay stations (RSs) usually require channel state information (CSI) and control signaling, resulting in high system overhead, latency, and complexity. In this paper, we propose a cooperation scheme for wireless networks, called stochastic cooperative communications based on geometrical probability (SCCGP). SCCGP has a low operational overhead and provides link capacity guarantee statistically. For cellular networks, a base station selects randomly a number of RSs in a hexagonal cell that have a fixed amplification factor, and the target user employs selective combining on the signal copies from multiple relaying paths. For ad hoc networks, the RSs are selected randomly in the circular area between a pair of communicating stations. Using a geometrical probability approach and the Cassini oval model, we derived the distribution functions of the cascaded path loss over a random two-hop relaying path, average received signal-to-noise ratio, and link capacity over multiple relaying paths. Furthermore, we transform the distribution functions into closed forms by using Taylor expansions. The mathematical proof and numerical results have shown that the closed-form distribution functions are valid and can be used to analyze the capacity of SCCGP and determine the minimum number of random RSs needed to satisfy an outage requirement. The SCCGP scheme can improve the user capacity considerably without the need of much coordination and CSI among the RSs. The derived distribution functions of the cascaded path loss over random two-hop paths can also be used in the interference management in multi-source-destination systems and other problems.

Appendix: Validation of the elliptic integrals

The Elliptic Integrals of the second kind in (11a) is

$$ \begin{array}{@{}rcl@{}} \mathcal{E}\!\!\left( \!2\beta_{A}\!\mid\!\frac{a^{4}}{d^{2}}\!\right) &=& {\int}_{0}^{2\beta_{A}} \sqrt{1-\frac{a^{4}}{d^{2}}\sin^{2}\theta} \mathrm{d}\theta \\ &=& {\int}_{0}^{2\beta_{A}} \sqrt{1-X_{\beta_{A}}} \mathrm{d}\theta, \end{array} $$

(34)

where $X_{\beta _{A}} = \frac {a^{4}}{d^{2}}\sin ^{2}\theta$ is defined for easy presentation. From Fig. 3 and trigonometry, we can get

$$ \begin{array}{@{}rcl@{}} d &=& D_{1}\!D_{2} \\ &=& \frac{a^{2} \sin\beta_{A}}{\sin\left( \frac{2\pi}{3} - \beta_{A}\right)} \sqrt{\frac{\sin^{2} \beta_{A}}{\sin^{2}\left( \frac{2\pi}{3} - \beta_{A}\right)} + 4 - \frac{2\sin\beta_{A}}{\sin\left( \frac{2\pi}{3} - \beta_{A}\right)}}. \end{array} $$

(35)

Then $X_{\beta _{A}}$ becomes (36).

$$ \begin{array}{@{}rcl@{}} X_{\beta_{A}} &=& \frac{a^{4}}{d^{2}}\sin^{2}\theta = \frac{\sin^{2}\left( \frac{2\pi}{3} - \beta_{A}\right)}{\sin^{2} \beta_{A}} \left[\frac{\sin^{2} \beta_{A}}{\sin^{2}\left( \frac{2\pi}{3} - \beta_{A}\right)}\right.\\ &&\left.+ 4 - \frac{2\sin\beta_{A}}{\sin\left( \frac{2\pi}{3} - \beta_{A}\right)}\right]^{-1} \sin^{2} \theta. \end{array} $$

(36)

According to Fig. 3, the phase of the intersection point, β_A, is in the range of $\beta _{A} \in \left [0,\ \frac {\pi }{2}\right ]$. The range of the integral variable 𝜃 in (34) is $\theta \in \left [0,\ 2\beta _{A} \right ]$. When $\beta _{A} \leq \frac {\pi }{4}$, $X_{\beta _{A}}$ is maximized at 𝜃 = 2β_A. When $\beta _{A} > \frac {\pi }{4}$, $X_{\beta _{A}}$ is maximized at $\theta = \frac {\pi }{2}$. Therefore, given β_A, the maximum of $X_{\beta _{A}}$ is in (37).

$$ \begin{array}{@{}rcl@{}} \max\limits_{\theta \in \left[0,\ 2\beta_{A} \right]}\left\{X_{\beta_{A}}\right\}= \max\limits_{\theta \in \left[0,\ 2\beta_{A} \right]} \left\{\frac{a^{4}}{d^{2}}\sin^{2}\theta\right\}= \left\{ \begin{array}{lll} \frac{\sin^{2}\left( \frac{2\pi}{3} - \beta_{A}\right)}{\sin^{2} \beta_{A}} \left[\frac{\sin^{2} \beta_{A}}{\sin^{2}\left( \frac{2\pi}{3} - \beta_{A}\right)} + 4 - \frac{2\sin\beta_{A}}{\sin\left( \frac{2\pi}{3} - \beta_{A}\right)}\right]^{-1} \sin^{2}2\beta_{A}, & \quad 0 < \beta_{A} \leq \frac{\pi}{4} \\\frac{\sin^{2}\left( \frac{2\pi}{3} - \beta_{A}\right)}{\sin^{2} \beta_{A}} \left[\frac{\sin^{2} \beta_{A}}{\sin^{2}\left( \frac{2\pi}{3} - \beta_{A}\right)} + 4 - \frac{2\sin\beta_{A}}{\sin\left( \frac{2\pi}{3} - \beta_{A}\right)}\right]^{-1}. & \quad \frac{\pi}{4} < \beta_{A} \leq \frac{\pi}{2} \end{array} \right. \end{array} $$

(37)

It can be observed from (37) that when $\beta _{A} = \frac {\pi }{4}$, $\max \left \{X_{\beta _{A}}\right \}$ achieves the maximum. Therefore, by plugging $\beta _{A} = \frac {\pi }{4}$ into (37), we can get (38).

$$ \begin{array}{@{}rcl@{}} \max\limits_{\beta_{A} \in \left[0,\ \frac{\pi}{2}\right]} \left\{\max\limits_{\theta \in \left[0,\ 2\beta_{A} \right]}\left\{X_{\beta_{A}}\right\}\right\} &=& \frac{\sin^{2}\left( \frac{2\pi}{3} - \frac{\pi}{4}\right)}{\sin^{2} \frac{\pi}{4}} \left[\frac{\sin^{2} \frac{\pi}{4}}{\sin^{2}\left( \frac{2\pi}{3} - \frac{\pi}{4}\right)}\right.\\ &&\left.+ 4 - \frac{2\sin\frac{\pi}{4}}{\sin\left( \frac{2\pi}{3} - \frac{\pi}{4}\right)}\right]^{-1} = 0.49. \end{array} $$

(38)

Since $X_{\beta _{A}}$ is bounded by 0.49, the Elliptic Integral in (11a) is valid.

Similarly, the Elliptic Integral of the second kind in the CDF in (11b) is

$$ \mathcal{E}\!\!\left( \!\pi\!\mid\!\frac{a^{4}}{d^{2}}\!\right) = {\int}_{0}^{\pi} \sqrt{1-\frac{a^{4}}{d^{2}}\sin^{2}\theta} d\theta = {\int}_{0}^{\pi} \sqrt{1-X_{\beta_{A}}} d\theta, $$

(39)

where the 𝜃 is in the range of $\theta \in \left [0,\ \pi \right ]$. Because this integral exists in the CDF under the condition of $\sqrt {d}>a$, the item $X_{\beta _{A}} = \frac {a^{4}}{d^{2}}\sin ^{2}\theta$ is maximized when $\theta = \frac {\pi }{2}$ and $d \rightarrow a^{2}$. Thus, we can obtain $\max \left \{X_{\beta _{A}}\right \} \rightarrow 1$. Since $X_{\beta _{A}}$ is bounded by 1, the Elliptic Integral in (11b) is validated.