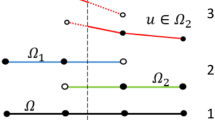
In a previous paper by Ryan and Shu [Ryan, J. K., and Shu, C.-W. (2003). \hboxMethods Appl. Anal. 10(2), 295–307], a one-sided post-processing technique for the discontinuous Galerkin method was introduced for reconstructing solutions near computational boundaries and discontinuities in the boundaries, as well as for changes in mesh size. This technique requires prior knowledge of the discontinuity location in order to determine whether to use centered, partially one-sided, or one-sided post-processing. We now present two alternative stencil choosing schemes to automate the choice of post-processing stencil. The first is an ENO type stencil choosing procedure, which is designed to choose centered post-processing in smooth regions and one-sided or partially one-sided post-processing near a discontinuity, and the second method is based on the edge detection method designed by Archibald, Gelb, and Yoon [Archibald, R., Gelb, A., and Yoon, J. (2005). SIAM J. Numeric. Anal. 43, 259–279; Archibald, R., Gelb, A., and Yoon, J. (2006). Appl. Numeric. Math. (submitted)]. We compare these stencil choosing techniques and analyze their respective strengths and weaknesses. Finally, the automated stencil choices are applied in conjunction with the appropriate post-processing procedures and it is determine that the resulting numerical solutions are of the correct order.
Similar content being viewed by others
References
Archibald R., Gelb A., and Yoon J. (2005). Polynomial fitting for edge detection in irregularly sampled signals and images. SIAM J. Numer. Anal. 43:259–279
Archibald, R., Gelb, A., and Yoon, J. (2006). Determining the locations of the discontinuities in the derivatives of functions. Appl. Numer. Math. (submitted).
Bramble J.H., and Schatz A.H. (1977). Higher order local accuracy by averaging in the finite element method. Math. Comput. 31:94–111
Cockburn, B. (1999). Discontinuous Galerkin methods for convection-dominated problems. In Barth, T. J., and Deconinck, H. (ed.), High-Order Methods for Computational Physics, Lecture Notes in Computational Science and Engineering, Vol. 9, Springer, pp. 69–224.
Cockburn B., Hou S., and Shu C.-W. (1990). The Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws IV: The multidimensional case. Math. Comput. 54:545–581
Cockburn B., Lin S.-Y., and Shu C.-W. (1989). TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws III: One dimensional systems. J. Comput. Phys. 84:90–113
Cockburn, B., Luskin, M., Shu, C.-W., and Süli, E. (1999). Post-processing of Galerkin methods for hyperbolic problems. In Karniadakis, G., Cockburn, B., and Shu, C.-W. (eds.), Proceedings of the International Symposium on Discontinuous Galerkin Methods, Lecture Notes in Computational Science and Engineering, Vol. 11, Springer, pp. 291–300.
Cockburn B., Luskin M., Shu C.-W., and Süli E. (2003). Enhanced accuracy by post- for finite element methods for hyperbolic equations. Math. Comput. 72:577–606
Cockburn B., and Shu C.-W. (1989). TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws II: General framework. Math. Comput. 52:411–435
Cockburn B., and Shu C.-W. (1991). The Runge–Kutta local projection \(\mathbb{P}^1\)-discontinuous-Galerkin finite element method for scalar conservation laws. Math. Model. Numer. Anal. (M 2 AN) 25:337–361
Cockburn B., and Shu C.-W. (1998). The Runge–Kutta discontinuous Galerkin method for conservation laws V: Multidimensional systems. J. Comput. Phys. 141:199–224
Cockburn B., and Shu C.-W. (2001). Runge–Kutta Discontinuous Galerkin methods for convection-dominated problems. J. Scientific Comput. 16:173–261
Gelb A., and Tadmor E. (2000). Detection of edges in spectral data II. Nonlinear enhancement. SIAM J. Numer. Anal. 38:1389–1408
Gottlieb S., and Shu C.-W. (1998). Total variation diminishing Runge–Kutta schemes. Math. Comput. 67:73–85
Gottlieb S., Shu C.-W., and Tadmor E. (2001). Strong stability preserving high-order time discretization methods. SIAM Rev. 43:89–112
Harten A., Engquist B., Osher S., and Chakravarthy S. (1987). Uniformly high order essentially non-oscillatory schemes I. SIAM J. Numer. Anal. 24:279–309
Harten A., Engquist B., Osher S., and Chakravarthy S. (1987). Uniformly high order essentially non-oscillatory schemes. J. Comput. Phys. 71:231–303
Liu X.-D., Osher S., and Chan T. (1994). Weighted essentially non-oscillatory schemes. J. Comput. Phys. 115:200–212
Ryan J.K., Shu C.-W., and Atkins H.L. Extension of a post-processing technique for the discontinuous Galerkin method for hyperbolic equations with application to an aeroacoustic problem. SIAM J. Scientific Comp. 26:821–843
Ryan J.K., and Shu C.-W. (2003). On a one-sided post-processing technique for the discontinuous Galerkin method. Methods Appl. Anal. 10(2):295–307
Shu C.-W., and Osher S. (1988). Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 77:439–471
Thomée V. (1977). High order local approximations to derivatives in the finite element method. Math. Comput. 31:652–660
Wahlbin, L. B. (1995). Superconvergence in Galerkin Finite Element Methods, Lecture Notes in Mathematics, Vol. 1605, Springer Verlag.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Archibald, R., Gelb, A., Gottlieb, S. et al. One-sided Post-processing for the Discontinuous Galerkin Method Using ENO Type Stencil Choosing and the Local Edge Detection Method. J Sci Comput 28, 167–190 (2006). https://doi.org/10.1007/s10915-006-9090-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-006-9090-z