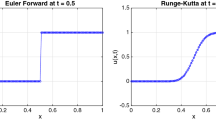
We discuss a new fifth-order, semi-discrete, central-upwind scheme for solving one-dimensional systems of conservation laws. This scheme combines a fifth-order WENO reconstruction, a semi-discrete central-upwind numerical flux, and a strong stability preserving Runge–Kutta method. We test our method with various examples, and give particular attention to the evolution of the total variation of the approximations.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Gottlieb S., Shu C.-W., and Tadmor E. (2001). Strong stability-preserving high order time discretization methods. SIAM Rev. 43:89–112
Harten A., Engquist B., Osher S., and Chakravarthy S. (1987). Uniformly high order accurate essentially non-oscillatory schemes III. J. Comp. Phys. 71:231–303
Jiang G.-S., and Shu C.-W. (1996). Efficient implementation of weighted ENO schemes. J. Comp. Phys. 126:202–228
Kurganov K., and Levy D. (2000). A Third-order semi-discrete central scheme for conservation laws and convection-diffusion equations. SIAM J. Sci. Comp. 22:1461–1488
Kurganov K., Noelle S., and Petrova G. (2001). Semi-discrete central-upwind schemes for hyperbolic conservation laws and Hamilton-Jacobi equations. SIAM J. Sci. Comp. 23:707–740
Kurganov K., and Petrova G. (2001). A Third-order semi-discrete genuinely multidimensional central scheme for hyperbolic conservation laws and related problems. Numer. Math. 88:683–729
Kurganov A., and Tadmor E. (2000). New high-resolution central schemes for nonlinear conservation laws and convection-diffusion equations. J. Comp. Phys. 160:241–282
Lax P.D. (1954). Weak solutions of nonlinear hyperbolic equations and their numerical computation. Comm. Pure Appl. Math. 7:159–193
LeVeque R.J. (1992). Numerical Methods for Conservation Laws. Lectures in Mathematics, Birkhuser, Basel
Levy D., Puppo G., and Russo G. (1999). Central WENO schemes for hyperbolic of conservation laws. Math. Model. Numer. Anal. 33:547–571
Levy D., Puppo G., and Russo G. (2000). Compact central WENO schemes for multidimensional conservation laws. SIAM J. Sci. Comp. 22:656–672
Levy D., Puppo G., and Russo G. (2000). On the behavior of the total variation in CWENO methods for conservation laws. Appl. Num. Math. 33:415–421
Levy, D., Puppo, G., and Russo, G. (2002). A fourth order central WENO scheme for multi-dimensional hyperbolic systems of conservation laws. SIAM J. Sci. Comp. 24,
Liu X.-D., Osher S., and Chan T. (1994). Weighted essentially non-oscillatory schemes. J. Comp. Phys. 115:200–212
Nessyahu H., and Tadmor E. (1990). Non-oscillatory central differencing for hyperbolic conservation laws. J. Comp. Phys. 87: 408–463
Qiu J., and Shu C.-W. (2002). On the construction, comparison, and local characteristic decomposition for high order central WENO schemes. J. Comp. Phys. 183:187–209
Shu C.-W., and Osher S. (1988). Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comp. Phys. 77:439–471
Sod G. (1978). A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws. J. Comp. Phys. 27:1–31
Spiteri R.J., and Ruuth S.J. (2002). A new class of optimal high-order strong-stability-preserving time discretization methods. SIAM J. Numer. Anal. 40:469–491
Woodward P., and Colella P. (1984). The numerical simulation of two-dimensional fluid flow with strong shocks. J. Comp. Phys. 54:115–173
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bryson, S., Levy, D. On the Total Variation of High-Order Semi-Discrete Central Schemes for Conservation Laws. J Sci Comput 27, 163–175 (2006). https://doi.org/10.1007/s10915-005-9046-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-005-9046-8