Abstract
Quantum mechanics introduces the concept of probability at the fundamental level, yielding the measurement problem. On the other hand, recent progress in cosmology has led to the “multiverse” picture, in which our observed universe is only one of the many, bringing an apparent arbitrariness in defining probabilities, called the measure problem. In this paper, we discuss how these two problems are related with each other, developing a picture for quantum measurement and cosmological histories in the quantum mechanical universe. In order to describe the cosmological dynamics correctly within the full quantum mechanical context, we need to identify the structure of the Hilbert space for a system with gravity. We argue that in order to keep spacetime locality, the Hilbert space for dynamical spacetime must be defined only in restricted spacetime regions: in and on the (stretched) apparent horizon as viewed from a fixed reference frame. This requirement arises from eliminating all the redundancies and overcountings in a general relativistic, global spacetime description of nature. It is responsible for horizon complementarity as well as the “observer dependence” of horizons/spacetime—these phenomena arise to represent changes of the reference frame in the relevant Hilbert space. This can be viewed as an extension of the Poincaré transformation in the quantum gravitational context. Given an initial condition, the evolution of the multiverse state obeys the laws of quantum mechanics—it evolves deterministically and unitarily. The beginning of the multiverse, however, is still an open issue.
Similar content being viewed by others
1 Introduction—The Basic Picture
This paper discusses two subjects: quantum mechanics and gravity, especially in the context of cosmology. Quantum mechanics introduced the concept of probability to physics at the fundamental level. This has led to the issue of the quantum-to-classical transition, in particular the measurement problem. Despite much progress, a complete and satisfactory picture, particularly the one including the entire universe, still seems missing.
Recent progress in cosmology has led to the “multiverse” picture—our observed universe may be one of the many in which low energy physical laws take different forms. This view is suggested by both observation and theory: it provides a successful understanding of the order of magnitude of the observed dark energy [1], and arises naturally as a result of eternal inflation [2–5] and the string landscape [6–9]. This elegant picture, however, suffers from the issue of predictivity—in the multiverse, any event that can happen will happen in infinitely many times, making any definition of probabilities extremely subtle [10–13]. Many proposals have been put forward to regulate these infinities, but they seem to be arbitrary, without relying on a solid fundamental principle. This arbitrariness of defining probabilities in the multiverse is called the measure problem.Footnote 1
More recently, it has been suggested that the above two issues are in fact related [14]. In particular, the probabilities in the eternally inflating multiverse must be defined based on the principles of quantum mechanics, which eliminates the problems and paradoxes plaguing some of the earlier measures. The probability formula given in Ref. [14] takes the form

where |Ψ(t)〉 is the state representing the entire multiverse, while  and
and  are projection operators implementing physical questions one would ask. This is (essentially) the Born rule. Indeed, the formula of Eq. (1) can be used to answer questions both regarding global properties of the universe and outcomes of particular experiments, providing complete unification of the eternally inflating multiverse and many worlds in quantum mechanics.
are projection operators implementing physical questions one would ask. This is (essentially) the Born rule. Indeed, the formula of Eq. (1) can be used to answer questions both regarding global properties of the universe and outcomes of particular experiments, providing complete unification of the eternally inflating multiverse and many worlds in quantum mechanics.
In Ref. [14], it was argued that the state |Ψ(t)〉 must be defined only in restricted spacetime regions—in and on the (stretched) apparent horizons—consistently with what we learned about quantum gravity in the past two decades: the holographic principle [15–17] and black hole complementarity [18–20]. In the cosmological context, however, the locations of horizons are “observer dependent.” What does this really mean? Moreover, Ref. [14] also discussed the meaning of spacetime singularities from the low energy viewpoint, and argued that it implies that the multiverse evolves asymptotically into a supersymmetric Minkowski world. Do these results have any implications for the problem of quantum measurement?
In this paper, we study these issues, developing a picture for quantum measurement and cosmological histories in the quantum mechanical universe. A crucial ingredient for our discussion is the structure of the Hilbert space corresponding to semi-classical spacetime, identified in Ref. [14] (and will be suitably refined here):

where  is the Hilbert (sub)space for a set of fixed semi-classical geometries
is the Hilbert (sub)space for a set of fixed semi-classical geometries  that have the same (stretched) apparent horizon
that have the same (stretched) apparent horizon  , as viewed from a local Lorentz frame of a fixed spatial point
p. It consists of the parts corresponding to the regions in and on the horizon,
, as viewed from a local Lorentz frame of a fixed spatial point
p. It consists of the parts corresponding to the regions in and on the horizon,  and
and  . (We will see that the complete Hilbert space for quantum gravity also has “intrinsically quantum mechanical” elements associated with spacetime singularities, but they are irrelevant for physical predictions.) Since consistency of quantum mechanics requires a quantum state to represent a physical configuration only in and on the horizon, the multiverse, which conventionally thought to exist beyond the horizon, must exist in probability space in the sense of a quantum superposition in the multiverse state. The probabilistic interpretation of the multiverse per quantum mechanics, therefore, is forced in the present framework.
. (We will see that the complete Hilbert space for quantum gravity also has “intrinsically quantum mechanical” elements associated with spacetime singularities, but they are irrelevant for physical predictions.) Since consistency of quantum mechanics requires a quantum state to represent a physical configuration only in and on the horizon, the multiverse, which conventionally thought to exist beyond the horizon, must exist in probability space in the sense of a quantum superposition in the multiverse state. The probabilistic interpretation of the multiverse per quantum mechanics, therefore, is forced in the present framework.
We argue that, as quantum mechanics has helped the measure problem in eternal inflation, the multiverse can help the measurement problem in quantum mechanics. In particular, the fact that we observe an ordered, classical world can be explained by a combination of spacetime locality and the fact that the multiverse ultimately evolves into a Minkowski (or singularity) world, which has an infinite-dimensional Hilbert space. This results in irreversibility of quantum measurement, despite the fact that the evolution of the multiverse state is unitary.
We also elucidate the meaning of the Hilbert space structure in Eq. (2). It is well known that to do Hamiltonian quantum mechanics, all the gauge redundancies must be fixed—and a theory of gravity has huge redundancies. Defining a state in Eq. (2) provides a simple way to fix these redundancies and to extract causal relations among events, which are physical (coordinate reparameterization invariant). In other words, we need to fix a reference frame when we describe a system with gravity quantum mechanically—this is the real meaning of the phrase: “physics must be described from the viewpoint of a single observer” in Ref. [14]. In particular, the location of a physical object/observer (with respect to “the origin of the coordinates” p) has physical meaning, so it needs to be included as a part of specification in conditions A and B when applying Eq. (1).
Since the Hilbert space  in Eq. (2) is defined on restricted spacetime regions, changes of the reference frame represented in
in Eq. (2) is defined on restricted spacetime regions, changes of the reference frame represented in  in general mix elements of different
in general mix elements of different  as well as the degrees of freedom associated with
as well as the degrees of freedom associated with  and
and  . (More generally, changing the reference frame can also mix elements of Eq. (2) with intrinsically quantum mechanical states associated with singularities.) This is the origin of horizon complementarity (mixture between different
. (More generally, changing the reference frame can also mix elements of Eq. (2) with intrinsically quantum mechanical states associated with singularities.) This is the origin of horizon complementarity (mixture between different  ) and of the “observer dependence” of cosmic horizons (mixture between the bulk and horizon degrees of freedom)! This general transformation can be viewed as an extension of the Lorentz/Poincaré transformation in the quantum gravitational context. It introduces more “relativeness” in physical descriptions—it makes even the concept of spacetime relative, as it mixes the bulk and horizon degrees of freedom in general.
) and of the “observer dependence” of cosmic horizons (mixture between the bulk and horizon degrees of freedom)! This general transformation can be viewed as an extension of the Lorentz/Poincaré transformation in the quantum gravitational context. It introduces more “relativeness” in physical descriptions—it makes even the concept of spacetime relative, as it mixes the bulk and horizon degrees of freedom in general.
Two key aspects of our picture of quantum measurement are dynamical evolution and the infinite dimensionality of the Hilbert space. We argue that spacetime locality—a special property of the time evolution operator—plays a crucial role in the evolution of a state. It leads to “amplification” of classical information [21–24] in a single component of the multiverse state. Schematically,

which shows that the classical information (i.e. that the spin is up) is amplified in a detector pointer and brain state of an observer (which can be amplified further). Note that since the faithful duplication of quantum information is prohibited [25], only classical information can be amplified, whose content is much smaller than the full quantum information.Footnote 2 At the same time, the dynamical evolution also leads to “branching” [26]: the state splits into many different components having well-defined classical configurations. For example, the initial e + e − state becomes a superposition of various components having well-defined particle configurations:
where we have omitted the coefficients for various components as well as momentum and spin indices. Through this process, the same quantum information can be distributed into multiple components over time; what the no-cloning theorem prohibits is the duplication of quantum information in a single component.
The evolution of the multiverse state experiences both these effects as it evolves in the full quantum gravitational Hilbert space. Schematically,
where the various letters indicate classical information. This evolution is deterministic and unitary, i.e., obeys the basic laws of quantum mechanics. The amplification generically occurs from a smaller system to larger systems. At the early stage of this process, the basis of the amplification is determined by the details of the system, as the standard analysis of decoherence shows [27]. On the other hand, at later stages, where the relevant systems are large, the amplification occurs in the basis corresponding to states having well-defined classical configurations, as a result of spacetime locality. Various components of the state will then correspond to different macroscopic worlds, which will eventually evolve into different supersymmetric Minkowski (or singularity) states. Since the Hilbert space dimension of Minkowski space is infinite, these worlds do not recohere—they really branch into different worlds.
The above picture provides a complete account for the process of quantum measurement in the eternally inflating multiverse. While not all the aspects of the dynamics described above are fully proven, the basic picture is strongly supported by recent progress on understanding the quantum-to-classical transition (e.g. [21–24, 27]). What are the implications of this in calculating physical probabilities in Eq. (1)? Physical information we can handle is only the “robust” kind, i.e. the one that can appear multiple times in physical systems. It therefore only makes sense to ask questions about information that is amplified in some component of the state. This corresponds to choosing projection operators  and
and  to extract only such information; in particular, it corresponds to projecting onto classically well-defined configurations when we ask questions about macroscopic systems.
to extract only such information; in particular, it corresponds to projecting onto classically well-defined configurations when we ask questions about macroscopic systems.
The framework described here provides a solid theoretical ground for asking any physical questions in the quantum universe. However, to make actual predictions in the context of the multiverse, e.g. of the value of a physical parameter we observe, we still need to know the explicit form of the time evolution operator as well as the initial condition for the multiverse state (except for a few special cases, including that for calculating the distribution of the cosmological constant [28]). In particular, knowing the complete evolution of the state requires understanding of the dynamics of the horizon degrees of freedom as well as the full string landscape. The former can be bypassed if we adopt the semi-classical approximation based on the “bulk density matrix” [14], ρ bulk(t)=Trhorizon|Ψ(t)〉〈Ψ(t)|, while the latter needs further progress in string theory. The initial condition for the multiverse state must be given by some external theory. Some (speculative) possibilities are presented in Ref. [14], but here we leave this issue aside and simply assume that an appropriate initial state is provided by some theory of initial conditions. (For a recent proposal to address the issue of initial conditions within the framework presented here, see Ref. [29].)
The organization of this paper is as follows. In the first half of the paper, Sects. 2, 3 and 4, we discuss quantum measurement without taking into account the effect of gravity. We discuss carefully how spacetime locality selects a basis in the Hilbert space, and we analyze quantum measurement in the context of applying quantum mechanics to the whole universe. We argue that the preferred basis for measurement is determined purely by the dynamics; in particular, the ultimate openness of the system is not required.
In the second half of the paper, Sects. 5, 6, 7 and 8, we discuss quantum mechanics in a system with gravity. Some of the results presented there were obtained in Ref. [14]; there are, however, some important refinements, e.g. on the precise definition of  in Eq. (2), the treatment of spacetime singularities, and a useful probability formula applying in many practical cases. We argue that complementarity as well as the observer dependence of horizons can be understood in a unified manner from the fact that changes of the reference frame are represented in the Hilbert space defined in restricted spacetime regions. We restate that the eternally inflating multiverse and many worlds in quantum mechanics are the same [14].
in Eq. (2), the treatment of spacetime singularities, and a useful probability formula applying in many practical cases. We argue that complementarity as well as the observer dependence of horizons can be understood in a unified manner from the fact that changes of the reference frame are represented in the Hilbert space defined in restricted spacetime regions. We restate that the eternally inflating multiverse and many worlds in quantum mechanics are the same [14].
Relations between quantum mechanics and the multiverse have been discussed in other work as well. Reference [30] considered the issue of basis selection in the context of the multiverse, although the resulting picture is crucially different from the one here, especially about unitarity of quantum mechanics. Earlier considerations of quantum mechanics in the multiverse/universe can be found in Refs. [31, 32]. The picture of the multiverse from a local viewpoint, which arises here as a consequence of quantum mechanics, has been promoted in the context of geometric cutoff measures; see Refs. [33–35] for example.
2 Probabilistic Interpretation of Quantum Mechanics
In this and the next two sections, we discuss how the probabilistic interpretation of quantum mechanics arises in a complete quantum mechanical system that includes a physical observer. We emphasize that the discussion does not require that the system is open as is often assumed in the treatment of quantum measurements. Having a precise understanding of this is crucial to apply quantum mechanics to the entire universe (or the eternally inflating multiverse).
Quantum Measurement a la von Neumann
Let us consider a simple nonrelativistic state in two dimensional Hilbert space. For definiteness, we take this to be a spin-1/2 system: |Ψ
sys〉=c
↑|↑〉+c
↓|↓〉, where |c
↑|2+|c
↓|2=1. The conventional Copenhagen interpretation says that if we measure the spin of this system at some time t=t
m, then we find it up or down with the probabilities P
↑=|c
↑|2 and P
↓=|c
↓|2, respectively. We may write this as  (α=↑,↓), where
(α=↑,↓), where  is the operator that projects onto the state with a definite spin α. After we measure a definite outcome, e.g. spin up, the wavefunction |Ψ
sys〉 of the system “collapses,” \(|\varPsi_{\mathrm{sys}}\rangle \stackrel{t=t_{\mathrm{m}}}{\longrightarrow} |\uparrow \rangle\).
is the operator that projects onto the state with a definite spin α. After we measure a definite outcome, e.g. spin up, the wavefunction |Ψ
sys〉 of the system “collapses,” \(|\varPsi_{\mathrm{sys}}\rangle \stackrel{t=t_{\mathrm{m}}}{\longrightarrow} |\uparrow \rangle\).
In a modern viewpoint, a physical measurement is treated as interactions between the measured system and an experimental apparatus, as discussed originally by von Neumann [36]. For t≪t m, the combined state of the spin and the apparatus is

where  represents the apparatus in a “ready” state. (We take the Schrödinger picture throughout.) After t≈t
m, the full state becomes
represents the apparatus in a “ready” state. (We take the Schrödinger picture throughout.) After t≈t
m, the full state becomes

due to the standard time evolution of the state. Here,  and
and  represent configurations of the apparatus after the measurement. This particular process, making the state of the apparatus entangled with that of the measured system, is called decoherence in the narrow sense [27]. A striking fact is that the dynamical evolution from Eq. (6) to Eq. (7) occurs very quickly; namely, a microscopic system can affect a macroscopic system drastically in a rather short timescale, in a way that they can no longer be considered independent systems.Footnote 3
represent configurations of the apparatus after the measurement. This particular process, making the state of the apparatus entangled with that of the measured system, is called decoherence in the narrow sense [27]. A striking fact is that the dynamical evolution from Eq. (6) to Eq. (7) occurs very quickly; namely, a microscopic system can affect a macroscopic system drastically in a rather short timescale, in a way that they can no longer be considered independent systems.Footnote 3
The Problem of the Preferred Basis
It is tempting to interpret Eq. (7) to show that the apparatus always measures either spin up or down, and not their superpositions. In fact, if the measured system is not a single spin, but a macroscopic object such as a chair, then the above discussion seems to explain the fact that we never observe superpositions of a macroscopic object in our everyday experience. Equation (7) alone, however, is not enough to show this because it can also be written in an arbitrary basis as [37]

Here,  (i=1,2) is a basis for the apparatus, and |i〉=∑
α=↑,↓
c
α
(U
−1)
αi
|α〉 the corresponding states for the measured system, where U is an arbitrary 2×2 unitary matrix. In particular, if |c
↑|=|c
↓|, then the states |1〉 and |2〉 form an orthogonal basis, so that they can be eigenstates of some Hermitian operator. How can one then say that the apparatus has measured the system in the {|↑〉,|↓〉} basis, not in the {|1〉,|2〉} basis?
(i=1,2) is a basis for the apparatus, and |i〉=∑
α=↑,↓
c
α
(U
−1)
αi
|α〉 the corresponding states for the measured system, where U is an arbitrary 2×2 unitary matrix. In particular, if |c
↑|=|c
↓|, then the states |1〉 and |2〉 form an orthogonal basis, so that they can be eigenstates of some Hermitian operator. How can one then say that the apparatus has measured the system in the {|↑〉,|↓〉} basis, not in the {|1〉,|2〉} basis?
A standard answer to this question is environmental decoherence [37–39], whose implementation in the present context goes as follows. We first regard the apparatus and spin as open quantum systems, interacting with some “environment” |E
0〉. We can then define the preferred states for the combined apparatus-spin system as the states that are least sensitive to the interaction with the environment, i.e. those that are least entangled with the environment by dynamical evolution. For instance, if the interaction between the apparatus and environment is such that  and
and  with 〈E
1|E
2〉→0, then the preferred states are the two terms in the right-hand side of Eq. (7) because each of them will not get entangled with the environment. The measurement is then claimed to be performed in this preferred state basis.
with 〈E
1|E
2〉→0, then the preferred states are the two terms in the right-hand side of Eq. (7) because each of them will not get entangled with the environment. The measurement is then claimed to be performed in this preferred state basis.
In this picture of environment-induced basis selection, the openness of quantum systems plays a crucial role in understanding measurement processes. In fact, such a picture is appropriate for the purpose of discussing consequences of quantum measurement performed in terrestrial experiments, which are indeed open. At the fundamental level, however, this raises the following question: what if we include the environment in the description of our quantum state? One might say that there is always some environment for any system in practice, but here we are talking about the fundamental issue. This question becomes particularly acute if we try to apply quantum mechanics to describe the entire universe, since then it is not even clear what one can take as an environment for the entire universe.
A line of reasoning like this has recently led the authors of Ref. [30] to claim that quantum mechanics is operationally well defined only under the existence of intrinsically inaccessible degrees of freedom, which they took to be those escaping a cosmic horizon in the eternally inflating multiverse. In this picture, quantum mechanical evolution is intrinsically irreversible—to obtain probabilistic interpretation of quantum mechanics, degrees of freedom outside the horizon must be traced out. Here we will argue differently—we need not introduce such irreversibility at the fundamental level. We argue that, as discussed in Ref. [14], the principles of quantum mechanics, including deterministic unitary evolution of the states, are fully respected if one describes physics as viewed from a single reference frame. The ambiguity of the basis is fixed by a feature in the dynamics, specifically spacetime locality as encoded in the algebra of (low energy) operators. We now see in detail what the implications of spacetime locality are in our context.
3 Physical Predictions and Spacetime Locality
Physical Information is in Matrix Elements
Suppose that at early times t≪t m, the detector apparatus has not yet interacted with the spin, as in Eq. (6). At t≈t m, the detector interacts with the spin, but we assume that the observer does not look at it until a later time t obs>t m. Finally, at t=t obs, the observer reads what the detector shows, and his/her brain state reacts accordingly. The state representing this entire system evolves as

Here, we do not necessarily consider that c ↑ and c ↓ are normalized as |c ↑|2+ |c ↓|2=1.
According to the standard rule of quantum mechanics, we expect that the probabilities for the observer to measure spin up and down should respectively be
ignoring the issue of the basis ambiguity. What is the precise meaning of this equation? The question we are asking is actually: “assuming that the observer learns the result of the experiment by reading the apparatus, what does he/she find?” This conditional probability is given by

where  is the operator projecting onto the state in which the observer learns the result to be α,
is the operator projecting onto the state in which the observer learns the result to be α,  and
and  onto the one in which he/she learns some result, whatever it is:
onto the one in which he/she learns some result, whatever it is:  .
.
The simple analysis above features two points. First, expressed in the form of conditional probabilities as in Eq. (11), physical predictions do not depend on how the state is written, including in what basis it is expanded. Second, our (more fundamental) formula of Eq. (11) reproduces Eq. (10) even if the state |Ψ(t)〉 contains additional terms that are not selected by the projection operator  . In fact, given an initial condition, the state at late times might contain a term representing a possibility that is not listed in Eq. (9); for example, the apparatus might break before the observer reads it, or the observer might change his/her mind and never look at the apparatus. Because of the way we asked the question, however, our answer always satisfies ∑
α
P(α|obs)=1. Namely, the possible additional terms in the state |Ψ(t)〉 are irrelevant for the question we are asking.
. In fact, given an initial condition, the state at late times might contain a term representing a possibility that is not listed in Eq. (9); for example, the apparatus might break before the observer reads it, or the observer might change his/her mind and never look at the apparatus. Because of the way we asked the question, however, our answer always satisfies ∑
α
P(α|obs)=1. Namely, the possible additional terms in the state |Ψ(t)〉 are irrelevant for the question we are asking.
As discussed in detail in Ref. [14], any physical question can be phrased in the form of a conditional probability; in the simplest setup, we can phrase it as: “Given what we know about our past light cone, A, what is the probability of that light cone to have properties B as well?” This eliminates the question of what the right basis is to expand the state. The answer is that it doesn’t matter. Once the question is phrased using the appropriate projection operators  and
and  (e.g.
(e.g.  and
and  in the above example), the desired probability P(B|A) is defined unambiguously.
in the above example), the desired probability P(B|A) is defined unambiguously.
Note that this, however, still leaves the question of “what is the right question to ask?” For example, if one asks the question in the form “what value of cosmological parameter X will I measure?,” then the ambiguity (of the question, not of the formalism) lies in the definition of “I” (or “we” unless the complete brain state is specified). This comprises a part of the measure problem in eternal inflation. The present framework offers the possibility of formulating it explicitly in terms of the projection operators used in the quantum mechanical probability formula, hence relating the measure problem with the issue of defining quantum mechanical probability.
Spacetime Locality and the Basis in Hilbert Space
Is there any ambiguity in writing operators  and
and  , and if so, wouldn’t that just be trading the basis ambiguity of states for that of operators? First of all, we note that it is appropriate to discuss the issue of basis in terms of operators, rather than states, as we will do here. This is because Hilbert space by itself does not carry any physical information other than its dimensionality—any (complex) Hilbert spaces having the same dimension are identical with each other. Of course, being operators acting on a vector space, quantum operators may also be written in an arbitrary basis. However, we now have dynamical structures that may distinguish some basis over the others. In particular, there can be a special basis in which algebraic relations among operators look particularly simple.
, and if so, wouldn’t that just be trading the basis ambiguity of states for that of operators? First of all, we note that it is appropriate to discuss the issue of basis in terms of operators, rather than states, as we will do here. This is because Hilbert space by itself does not carry any physical information other than its dimensionality—any (complex) Hilbert spaces having the same dimension are identical with each other. Of course, being operators acting on a vector space, quantum operators may also be written in an arbitrary basis. However, we now have dynamical structures that may distinguish some basis over the others. In particular, there can be a special basis in which algebraic relations among operators look particularly simple.
Consider a (special) relativistic system. At length scales larger than the possible quantum gravity scale (and the entropy density lower than that of a black hole), such a system is described by quantum field theory [40]. Suppose there is only a single species of particles, represented by a quantum field ϕ(x) with x being spatial coordinates. The field ϕ(x) at different x should be regarded as different operators, which satisfy
where π(x) is a conjugate momentum of ϕ(x), and [ , ]∓ represents a commutator and anti-commutator if the particle is a boson and fermion, respectively. Here, we have discretized spatial coordinates x for presentation purposes. An important point is that in this “local field” basis, the time evolution operator \(U(t_{1},t_{2}) = e^{-iH(t_{1}-t_{2})}\) takes a particularly simple form
where ϵ i (i=0,1,2,…) runs only over a very small subset of the coordinates around \(\boldsymbol{\epsilon}_{0} \equiv{\bf0}\) (typically “nearest neighbors”). This is not the case if we use an arbitrary basis ϕ(z)=∑ x c zx ϕ(x) (c zx ≠δ zx ). Namely, if we write H in terms of ϕ(z) and π(z) in the form of Eq. (13), then ϵ i need not run only over a very small subset of the coordinates for generic c zx .
The existence of a special basis satisfying Eq. (13) is what we call spacetime locality. This is a property of nature whose origin is not yet fully understood—it is simply an empirical fact that there is such a basis at length scales that have been probed experimentally so far.Footnote 4 This property, however, is crucial in selecting a particular basis in Hilbert space in which a simple description of physics is obtained. Specifically, consider a set of (time-independent) states |κ m 〉 that are eigenstates of the particle-number operators N x for all x (not z):
These states are special in that they have well-defined configurations in physical space x. Furthermore, since the set of states in Eq. (14) spans Fock space, it can form an orthonormal basis of Hilbert space; namely, an arbitrary state |Ψ(t)〉 may be written as a superposition
where c m (t) are complex functions and 〈κ m |κ n 〉=δ mn . Note that the particular basis here, |κ m 〉, has been chosen such that an algebraic relation between operators—specifically the form of H in terms of ϕ(x) and π(x)—takes a simple form in that basis. In fact, the very concept of “configurations in space” arises as a result of the special property in Eq. (13); without that, x could not even be interpreted as spatial coordinates.
We should emphasize that the choice of the Hilbert space basis discussed here does not by itself address the issue of basis selection for quantum measurement described in Sect. 2, although the former is needed for the discussion of the latter. Indeed, the choice described here is, in some sense, “a matter of convenience,” in that we can also describe physics using the ϕ(z) basis in principle (because the matrix elements, appearing in the probability formula, do not depend on the basis). In this basis, however, the time evolution operator has an extremely complicated form, which completely obscures the fact that the dynamics respects spacetime locality. Therefore, in practice one always needs to choose a Hilbert space basis associated with locality: either |κ m 〉 in Eq. (14) or a basis that has a simple relation to it (such as the momentum basis).
What Physical Questions May One Ask?
Let us choose the “locality basis” |κ
m
〉, given in Eq. (14). Then there is no ambiguity in expanding states as in Eq. (15). The question, however, still remains: how can we choose the “correct form” for projection operators  and
and  appearing in the probability formula? Experience says that all the information we can explicitly handle (in the sense that it can be duplicated in physical systems) is given in the form of, e.g., Eq. (11)—i.e. by operators projecting onto states that have well-defined macroscopic configurations in the phase space (up to some uncertainties). Why is that?
appearing in the probability formula? Experience says that all the information we can explicitly handle (in the sense that it can be duplicated in physical systems) is given in the form of, e.g., Eq. (11)—i.e. by operators projecting onto states that have well-defined macroscopic configurations in the phase space (up to some uncertainties). Why is that?
In general, states having well-defined macroscopic configurations are obtained as superpositions of |κ m 〉 that have “similar” spatial configurations. For each macroscopic configuration i, we have a set of n i corresponding microstates: \(|\psi^{\mathrm{(i)}}_{a}\rangle = \sum_{m} f_{a,m}^{(i)} | \kappa_{m} \rangle\) (a=1,…,n i ), which we collectively call |α i 〉. Here, \(f_{a,m}^{(i)}\) for each (i,a) play the role of a smearing function in position space, ensuring that the configuration has a well-defined momentum at the macroscopic level. The projection operator onto macroscopic configuration i can then be defined as \(| \alpha_{i} \rangle\langle\alpha _{i}| \equiv \sum_{a=1}^{n_{i}} |\psi^{\rm(i)}_{a}\rangle\langle\psi^{\mathrm{(i)}}_{a}|\), where we have taken \(\langle\psi^{\rm(i)}_{a} | \psi^{\rm(i)}_{b} \rangle = \delta_{ab}\). Since \(\langle\psi^{\rm(i)}_{a} | \psi^{\rm(j)}_{b} \rangle \approx0\) for different macroscopic configurations i≠j, these projection operators satisfy P i P j ≈P j P i ≈0 for i≠j, where P i =|α i 〉〈α i |.
The issue is why physical questions we ask are always phrased in terms of  and
and  that take the form
that take the form

(and similarly for  ), where i∈A implies that the sum is taken for the configurations that satisfy condition A. In particular, what is wrong with using |α
i
〉 corresponding to a superposition of macroscopically different configurations, i.e. microstates \(| \psi^{\rm(i)}_{a} \rangle\) in which the expansion coefficients \(f_{a,m}^{(i)}\) have significant supports from macroscopically different configurations m? This strong restriction on possible questions we may ask is the essence of basis selection for quantum measurement, and composes what we call the quantum-to-classical transition. Its origin is in the dynamics, specifically spacetime locality as encoded in Eq. (13), as we will discuss in the next section.
), where i∈A implies that the sum is taken for the configurations that satisfy condition A. In particular, what is wrong with using |α
i
〉 corresponding to a superposition of macroscopically different configurations, i.e. microstates \(| \psi^{\rm(i)}_{a} \rangle\) in which the expansion coefficients \(f_{a,m}^{(i)}\) have significant supports from macroscopically different configurations m? This strong restriction on possible questions we may ask is the essence of basis selection for quantum measurement, and composes what we call the quantum-to-classical transition. Its origin is in the dynamics, specifically spacetime locality as encoded in Eq. (13), as we will discuss in the next section.
4 Classical Reality in the Quantum Mechanical Universe
In this section, we discuss the origin of the following basic observational facts: (i) probabilistic processes in quantum mechanics are well described by density matrices that are diagonal in the “classical state basis” |α i 〉 at least for macroscopic systems; (ii) a measurement selects an outcome; namely, we can ignore other possible outcomes after a measurement is performed. In the standard treatment of these problems, the openness of a system is emphasized [21–24, 27]. Here we ask if the openness is really necessary at the fundamental level to account for these features. We will argue that the answer is no—the quantum-to-classical transition may occur consistently with observation even in a closed, finite dimensional quantum mechanical system.
On the other hand, we will also argue that cosmology based on a finite dimensional system with a generic initial condition fails to explain another basic observational fact: (iii) we observe an ordered world, i.e., we perceive a world that obeys consistent laws of physics. This argument will force us to consider that the Hilbert space for the entire universe (multiverse) is infinitely large:  , unless we abandon unitarity of quantum mechanical evolution or genericity of the quantum state.
, unless we abandon unitarity of quantum mechanical evolution or genericity of the quantum state.
A Double-Slit Experiment in a Large System
We begin by a standard analysis of the double-slit experiment, which sets the stage for later discussions. For the moment, we can be agnostic about whether the entire system is open or closed. The setup of the experiment is such that an electron, initially prepared at slits as \(| \psi_{e,{\mathrm{init}}} \rangle= \frac{1}{\sqrt{2}} (| 1 \rangle+ | 2 \rangle)\) evolves according to |1〉→∫dx ψ 1(x)|x〉 and |2〉→∫dx ψ 2(x)|x〉. Here, |1〉 and |2〉 represent the electron localized at slits 1 and 2, respectively, while |x〉 represents the electron localized at position x on the screen.
The entire system is initially in the state  , where
, where  represents the detector in a ready state and |R〉 the degrees of freedom that are not included in the electron or detector state. Assuming that there is no interaction between the experimental apparatus and the rest of the world, this state evolves into
represents the detector in a ready state and |R〉 the degrees of freedom that are not included in the electron or detector state. Assuming that there is no interaction between the experimental apparatus and the rest of the world, this state evolves into

Here, we have assumed that the combined electron and detector system evolves as  , where |0〉 implies that the electron has been absorbed into the apparatus, and
, where |0〉 implies that the electron has been absorbed into the apparatus, and  represents the status of the detector showing that the electron has arrived at x on the screen. The probability density of finding the electron at x in this experiment is then given by
represents the status of the detector showing that the electron has arrived at x on the screen. The probability density of finding the electron at x in this experiment is then given by

where  . Plugging Eq. (17) into Eq. (18), we obtain the standard result: \(P(x|{\mathrm{exp}}) \propto|\psi_{1}(x)|^{2} + |\psi_{2}(x)|^{2} + 2\, {\mathrm{Re}}\{ \psi_{1}(x) \psi_{2}^{*}(x) \}\). Here, we have used
. Plugging Eq. (17) into Eq. (18), we obtain the standard result: \(P(x|{\mathrm{exp}}) \propto|\psi_{1}(x)|^{2} + |\psi_{2}(x)|^{2} + 2\, {\mathrm{Re}}\{ \psi_{1}(x) \psi_{2}^{*}(x) \}\). Here, we have used  .
.
The question, again, is why the result of the experiment is described by Eq. (18). In particular, why do we perceive the world in such a way that a macroscopic quantum system decoheres in the classical state basis, in this case the location of the pointer of the apparatus? In the standard explanation due to environment-induced basis selection, the openness of a system plays a crucial role. Below, we will obtain (essentially) the same result without invoking an openness of the whole system, which elucidates the real origin of the basis selection in quantum measurement.
Dynamical Selection of a Measurement Basis—Spacetime Locality
Let us keep following the state of the system after the double-slit experiment was performed. Denoting the state after the double-slit measurement by |ψ
x
(t)〉, where  , the state of the entire system is given by |Ψ(t)〉=∫dx
c
x
|ψ
x
(t)〉, where c
x
≡(ψ
1(x)+ψ
2(x))/(∫dy |ψ
1(y)+ψ
2(y)|2)1/2.
, the state of the entire system is given by |Ψ(t)〉=∫dx
c
x
|ψ
x
(t)〉, where c
x
≡(ψ
1(x)+ψ
2(x))/(∫dy |ψ
1(y)+ψ
2(y)|2)1/2.
Now, let us imagine that some other experiment is performed in this system at a late time t exp. This experiment will involve only a very small subset of the degrees of freedom in |Ψ(t)〉, as we consider that the entire system is very large. We isolate these degrees of freedom by writing |ψ x (t)〉=|ϕ x (t)〉⊗|r x (t)〉:
where the first factor represents degrees of freedom associated with the experiment while the second the rest. The outcome of this experiment can be calculated, using the probability formula based on matrix elements as

where  is the projection operator acting on |ϕ
x
(t)〉 selecting the situation where the experiment is performed with a definite outcome A.
is the projection operator acting on |ϕ
x
(t)〉 selecting the situation where the experiment is performed with a definite outcome A.
The expression of Eq. (20) contains terms representing interference between different outcomes of the first, double-slit experiment, i.e. x and y with x≠y. These terms, however, disappear if 〈r
x
(t
exp)|r
y
(t
exp)〉≪1 for x≠y, in which case we obtain  . Here, we have assumed
. Here, we have assumed  , i.e. the second experiment occurs no matter what the outcome of the double-slit experiment. The probabilities for the outcomes of the two experiments now follow what we expect classically:
, i.e. the second experiment occurs no matter what the outcome of the double-slit experiment. The probabilities for the outcomes of the two experiments now follow what we expect classically:
Note that the result of the second experiment may depend on that of the first, as indicated by the subscript x on the second probability factor.
The condition used above to obtain Eq. (21), 〈r
x
(t
exp)|r
y
(t
exp)〉≪1 for x≠y, is exactly what we expect. Since the detector states  for different x have different macroscopic configurations and since the Hamiltonian of the system is local, the future states corresponding to different
for different x have different macroscopic configurations and since the Hamiltonian of the system is local, the future states corresponding to different  are almost orthogonal: 〈ψ
x
(t)|ψ
y
(t)〉∼δ(x−y).Footnote 5 This implies that 〈r
x
(t)|r
y
(t)〉∼δ(x−y) because |ϕ
x
(t)〉 is only a very small subset of the entire degrees of freedom in |ψ
x
(t)〉, leading to Eq. (21).
are almost orthogonal: 〈ψ
x
(t)|ψ
y
(t)〉∼δ(x−y).Footnote 5 This implies that 〈r
x
(t)|r
y
(t)〉∼δ(x−y) because |ϕ
x
(t)〉 is only a very small subset of the entire degrees of freedom in |ψ
x
(t)〉, leading to Eq. (21).
The argument given above, however, is not by itself sufficient to explain selection of the measurement basis, because the same analysis applies to any (not necessarily classical state) basis z=∫dx
r
zx
x satisfying ∫dx
r
zx
r
z′x
=δ(z−z′). The selection happens because “amplification” occurs (only) in a particular basis (called quantum Darwinism) [21–24]. Schematically, we can write as  , where the last expression implies that the same classical information, i.e. “the double-slit experiment measured the electron at x,” is available (independently) to many subcomponents of the system. For example, for a superposition of two outcomes after the double-slit experiment, this gives
, where the last expression implies that the same classical information, i.e. “the double-slit experiment measured the electron at x,” is available (independently) to many subcomponents of the system. For example, for a superposition of two outcomes after the double-slit experiment, this gives

Note that this is different from the cloning of quantum information, which would yield

Namely, only selected information, that corresponding to classical states |α i 〉, can be amplified. The origin of the particular evolution in Eq. (22) is the special form of the evolution operator, Eq. (13)—the classical state basis is selected as a dynamical consequence of spacetime locality. While this is yet to be proven in the general case, analyses of simple quantum mechanical systems [21–24] strongly suggest that to be the case.
The property of Eq. (22) for |α i 〉, as well as their approximate orthogonality, imply that if n−1 successive experiments are performed after the double-slit experiment, we obtain
This is the classical probability formula. The subscripts in P’s on the right-hand side indicate that the results of earlier experiments are available independently to many successive experiments, just by accessing small subsets of the entire system. This forms a crucial ingredient for classical objectivity, according to the quantum Darwinism picture [21–24]. While this picture is not fully proved, we assume that it addresses the issue of appearance of classical worlds as originally envisioned. We emphasize that the basis of decomposition in Eq. (24) here is determined dynamically. In fact, the very existence of a special basis in which the classical formula of Eq. (24) is true is a dynamical consequence of spacetime locality.
The argument presented here is the heart of the basis selection in describing any experimental result in a way that our classical intuition is manifest. It also provides a real rationale behind Eq. (16), which was chosen to be diagonal in the classical state basis |α i 〉. The information about classical configuration |α i 〉 is that which can be amplified by the dynamical evolution—this is not very surprising given that |α i 〉’s are deeply related to the locality basis states, which are determined by the form of the time evolution operator. Questions we ask are about information that can be objectively accessed by multiple physical processes, hence the form of Eq. (16). Note that by integrating out |R〉 as well as all the histories after t=0, this reproduces the usual einselection criterion in the decoherence paradigm. The argument here, however, makes it clear that the basis selection has nothing to do with the ultimate openness of the system—indeed, the present argument still applies even if the entire system is finite dimensional, being subject to thermalization and recurrences at later times. The origin of the basis selection lies entirely in the dynamics—specifically, the fact that the time evolution operator takes a special form of Eq. (13) in the locality basis.
Ordered Observations Require Infinitely Large Hilbert Space for a Generic State
Does the preceding argument ensure that the two features listed at the beginning of this section, (i) and (ii), are valid in any quantum system described by a local theory? In other words, can we always consider that a sufficiently macroscopic measurement collapses the wavefunction to one of the possible states having a well-defined classical configuration?
The answer is yes, but not trivially if the system is finite dimensional and we are interested in arbitrarily long timescales. In this case the entire system thermalizes at ∼t th, after which it occasionally experiences rare fluctuations producing low entropy regions, and eventually comes back to a state arbitrarily close to the original state at timescale \(t_{*} \sim e^{S_{\mathrm{th}}}\), where S th is the thermal entropy of the system. This picture applies regardless of the details of the system, as long as quantum mechanical evolution is unitary and the initial condition is generic, which we assume here. Since the process of producing low entropy fluctuations generically involves interferences between macroscopically different terms, one might think that replacing |Ψ fin〉 by a collapsed state |Ψ col〉 gives an obviously wrong answer. This conclusion, however, is too naive.
Consider a process in which a thermal state having a large coarse-grained entropy, ∼S th, fluctuates into a state with a low coarse-grained entropy and then evolves back to another thermal state: \(| \varPsi_{\sim S_{\mathrm{th}}} \rangle\rightarrow| \varPsi '_{S_{\mathrm{low}}} \rangle\rightarrow| \varPsi''_{\sim S_{\mathrm{th}}} \rangle\), where we have denoted the coarse-grained entropy of a state by the subscript (S low≪S th). One might think that the first part of this process, \(| \varPsi_{\sim S_{\mathrm{th}}} \rangle\rightarrow| \varPsi '_{S_{\mathrm{low}}} \rangle\), looks like the “classical-to-quantum transition,” as it involves recoherence of macroscopically different configurations, thus contradicting observation. This is, however, not true. Because of the reversibility of quantum evolution, the process is given, with high probability, by the time reversal of a usual entropy increasing process [41]:
where a state with a bar is the CPT conjugate of the corresponding state without. Since any physical observer is necessarily a part of the system, the two processes in Eq. (25) look identical to him/her—these are really time reversals of each other including memory states of the observer. In particular, for an “observer,” who can arise only as a part of such a fluctuation, the world always appears to obey properties (i) and (ii): the standard rules of Copenhagen quantum mechanics (as well as the second law of thermodynamics). What is wrong, then, with the picture that the universe is a finite dimensional quantum mechanical system, with the history repeating with the period of order t ∗? The problem is that a fluctuation, which for internal observers appears as two “regular worlds” related by CPT, generically has “initial conditions” (i.e. \(|\varPsi'_{S_{\mathrm{low}}}\rangle\) and \(|\bar{\varPsi}'_{S_{\mathrm{low}}}\rangle\) in Eq. (25)) that are not expected to be obtained by evolving the system from a state having a smaller coarse-grained entropy. Indeed, according to standard equilibrium thermodynamics, the probability distribution of the “initial conditions” should follow ∝e −F/T, where F=M fluc−TS low is the free energy associated with the configurations at the bottom of entropy dips. This implies that if we consider processes that involve any “perceptions,” they will be overwhelmingly dominated by those observing random, irregular worlds, as opposed to a regular world obeying consistent laws of physics, contradicting what we actually observe. This is nothing but the well-known Boltzmann brain problem [42] as applied to a general finite dimensional system.
Hence a description of the universe consistent with our observation, i.e. item (iii) listed at the beginning of this section, is obtained only if the thermalization timescale of the system, t
th, is (much) larger than the timescale of interest t. Since \(t_{*} \sim e^{S_{\mathrm{th}}} \gg t_{\mathrm{th}}\) and  , where
, where  is the Hilbert space dimension of the entire system, this implies
is the Hilbert space dimension of the entire system, this implies  . In particular, this implies that if we want to describe the entire history of the universe (t→∞), which we must do if quantum mechanical evolution is fundamentally unitary, then we need to take
. In particular, this implies that if we want to describe the entire history of the universe (t→∞), which we must do if quantum mechanical evolution is fundamentally unitary, then we need to take  , i.e. the Hilbert space describing the quantum universe must be infinitely large.Footnote 6
, i.e. the Hilbert space describing the quantum universe must be infinitely large.Footnote 6
As we will see in Sect. 7, this condition is satisfied in the eternally inflating multiverse because the multiverse evolves asymptotically to a supersymmetric Minkowski (or singularity) world, which contains an infinite number of states. This completes an ultimate picture for quantum measurement—a quantum measurement is a process in which a coherence existing in a (microscopic) system is dissipated into larger systems, ultimately into states in a supersymmetric Minkowski (or singularity) world. Recoherence of the resulting, macroscopically different worlds does not occur because of an infinitely large coarse-grained entropy of Minkowski (and singularity) space.
5 Spacetime Locality in Theories with Gravity
We have seen that spacetime locality plays a crucial role in quantum measurement processes. In theories with gravity, however, this property is not automatically guaranteed. In particular, if we take wrong hypersurfaces to quantize the system, theories are not local even at distances much larger than the quantum gravity scale.
In the rest of the paper, we study the structure of the Hilbert space describing the entire quantum universe, starting with the well-known discussion on quantum mechanics of black holes. Some of the results presented in the following were obtained in Ref. [14]. There are, however, some important refinements, including the treatment of spacetime singularities and a useful probability formula that applies in many practical cases. We also provide a clearer argument leading to the results, and discuss their meaning, especially in the context of physical measurements.
Black Hole Complementarity
Here we review black hole complementarity [18–20, 43], which we assume gives the correct description of black hole physics.
Consider a traveler falling into a black hole. From the point of view of a distant observer, this traveler is absorbed into the horizon, which has an extremely high local temperature (because of gravitational blueshift). Assuming that quantum mechanics is valid, the original information carried by the traveler must be stored at the horizon, which will eventually come out as Hawking radiation. In the limit that the black hole is very large, this implies that the evolution of the system is unitary on the Hilbert space

where  and
and  represent the Hilbert space factors associated with the degrees of freedom on and outside the horizon, respectively. (Strictly speaking, the horizon here means the stretched horizon, which is ∼l
s
away from the mathematical horizon, where l
s
is the string length.) Here, the tensor product structure of the horizon and bulk Hilbert space factors is postulated to preserve locality as much as possible. Whether this can indeed be the case is under active debate. For alternative views, see e.g. Ref. [44].
represent the Hilbert space factors associated with the degrees of freedom on and outside the horizon, respectively. (Strictly speaking, the horizon here means the stretched horizon, which is ∼l
s
away from the mathematical horizon, where l
s
is the string length.) Here, the tensor product structure of the horizon and bulk Hilbert space factors is postulated to preserve locality as much as possible. Whether this can indeed be the case is under active debate. For alternative views, see e.g. Ref. [44].
On the other hand, from the point of view of the falling traveler, there is nothing special about the horizon, and physics is described in the Hilbert space

where  is the Hilbert space associated with the degrees of freedom inside the horizon. Again, assuming the validity of quantum mechanics, the evolution of the system is unitary on the above Hilbert space (until the singularity is hit).
is the Hilbert space associated with the degrees of freedom inside the horizon. Again, assuming the validity of quantum mechanics, the evolution of the system is unitary on the above Hilbert space (until the singularity is hit).
Now, let us consider the fate of the information originally carried by the traveler. From the distant observer’s viewpoint, elements of Eq. (26) will be mapped, after the back hole evaporates, into those of the Hilbert space associated with spacetime without the black hole:  . The information is then first in
. The information is then first in  , and later in
, and later in  . From the falling traveler’s viewpoint, on the other hand, this information is in
. From the falling traveler’s viewpoint, on the other hand, this information is in  . A problem arises when we mix these two viewpoints in the global spacetime picture. In this picture, we can draw spacelike hypersurfaces—often called nice slices—on which the information exists both in Hawking radiation and inside spacetime. From a general relativistic point of view, there is nothing wrong with defining states on such hypersurfaces. This, however, leads to contradiction with the laws of quantum mechanics, specifically the no-cloning theorem [25].
. A problem arises when we mix these two viewpoints in the global spacetime picture. In this picture, we can draw spacelike hypersurfaces—often called nice slices—on which the information exists both in Hawking radiation and inside spacetime. From a general relativistic point of view, there is nothing wrong with defining states on such hypersurfaces. This, however, leads to contradiction with the laws of quantum mechanics, specifically the no-cloning theorem [25].
Black hole complementarity asserts that the problem arises because we have taken the global viewpoint that does not have any operational meaning. Indeed, because of the existence of the horizon, no physical observer can obtain the same information from inside region and Hawking radiation [45, 46]. This implies that if quantum mechanics is defined on equal-time hypersurfaces that pass through both the inside and outside information, then the low energy theory (not just states) must be non-local in such a way that these spatially separated degrees of freedom are not independent. Alternatively, if we want to keep locality in our low energy description of nature (which we do), then the Hilbert space should be restricted to the one associated with appropriate spacetime regions, e.g. Eq. (26) or (27)—including both the inside spacetime region and Hawking radiation in a single description is overcounting.
Quantum States are Defined in Restricted Spacetime Regions
How should we then define quantum states without sacrificing locality of the theory at distances larger than the quantum gravity scale? In Ref. [14], it is proposed that:
-
The states are defined on the past light cone bounded by the “(stretched) apparent horizon.” Following the refinement in Ref. [47], here we take this horizon as the closer of the “observer horizon” and the surface on which the expansion of a light ray generating the past light cone turns from positive to negative. The former is defined in turn as a surface on which local proper acceleration of a constant affine parameter point along a light ray generating the cone exceeds the cutoff scale, where the affine parameter is normalized such that it agrees with the radial coordinate of a local Lorentz frame erected at the tip of the light cone. (This surface is reduced to the conventionally defined stretched horizon in the static limit; see Ref. [47] for details.) The degrees of freedom exist both inside and on the (stretched) apparent horizon, and the system is described as viewed from a local Lorentz frame at the tip of the light cone.
-
The definition above provides the simplest way of avoiding the overcounting of the type described above, making the time evolution operator local at distances larger than the quantum gravity scale. The evolution of a quantum state is deterministic and unitary in this Hilbert space (until spacetime singularities are hit; see Sect. 7).
Let us consider de Sitter space. Following the above definition, the states on this background are given on the past light cone of some fixed center p. The structure of the Hilbert space, of which these states are elements, is thus

where  and
and  are the Hilbert space factors associated with the degrees of freedom on and inside the stretched horizon, respectively. On a fixed de Sitter background, the evolution of a state is unitary in the space of Eq. (28). In particular, information leaving the horizon of p in the global spacetime picture is regarded as being stored in
are the Hilbert space factors associated with the degrees of freedom on and inside the stretched horizon, respectively. On a fixed de Sitter background, the evolution of a state is unitary in the space of Eq. (28). In particular, information leaving the horizon of p in the global spacetime picture is regarded as being stored in  , which can later be sent back to
, which can later be sent back to  in the form of subtle quantum correlations in Hawking radiation. Note that, in this description, a physical observer need not be at p, which simply plays the role of “the origin of the coordinates.” (A nontrivial consistency check of this picture was given in Appendix C of Ref. [14].)
in the form of subtle quantum correlations in Hawking radiation. Note that, in this description, a physical observer need not be at p, which simply plays the role of “the origin of the coordinates.” (A nontrivial consistency check of this picture was given in Appendix C of Ref. [14].)
The examples considered above clearly demonstrate that the restriction of spacetime regions is crucial to keep locality of the low energy theory while being consistent with quantum mechanics. Assuming that information absorbed into the de Sitter horizon can be retrieved later (which is necessary for stable de Sitter space to be regarded as a finite dimensional system, as suggested by the holographic principle), quantum states cannot be defined on hypersurfaces that pass through both Hawking radiation and outside spacetime containing the same information. This situation is analogous to that in the black hole case. The only difference is that the de Sitter horizon is “observer dependent”: its location changes depending on from whose point of view the system is described.
In Ref. [14], the definition of quantum states considered above was stated as: the system is described from the viewpoint of a single “observer” (geodesic). Here we phrase the same thing as: physics should be described using a single reference frame, which captures the essential physics better.
6 Importance of Fixing a Reference Frame
Fixing a Gauge—Physics Should be Described in a Single Reference Frame
What are observables in physical theories? They should be “gauge invariant,” i.e. quantities that do not depend on arbitrary parameterizations of the system corresponding to the redundancy of the description. In theories with gravity, the coordinatization of spacetime is precisely one such parameterization, so it might be thought that only observables are certain global quantities, e.g. the ones associated with the topology of spacetime. This is not true—causal relations among events are invariant under general coordinate transformations, and thus are physically observable.
It is well known that to do Hamiltonian quantum mechanics, all the gauge redundancies must be fixed. A theory of gravity has huge redundancies associated with general coordinate transformations. The definition of the states described in the previous section provides a simple way to fix these redundancies and extract causal relations among the events. The origin of a special point p (i.e. the tip of the past light cone used to define states) is now clear—it arises from the fact that the theory is invariant under local spatial translations and that we need to fix the resulting redundancies. By choosing a local Lorentz frame with the origin at p, all the redundancies associated with p are fixed. While this prescription by itself does not completely determine the gauge for general covariance, fixing the residual ones, coming from coordinate transformations on the past light cone, is simple conceptually and gives only minor effects on the overall picture.
Together with the restriction of spacetime within the (stretched) apparent horizons, this comprises the statement in Ref. [14] that “physics is described from the viewpoint of a single observer.” The choice of the local Lorentz frame at p implies that the tip of the light cone follows a geodesic at the semi-classical level. The overcounting of the type encountered before does not arise, and the time evolution operator is local at large distances.
Hilbert Space for Dynamical Spacetime—Analogy with Fock Space
We now construct the Hilbert space for dynamical spacetime, following the discussion so far. To do so, it is instructive to draw a close analogy with the construction of the Hilbert space in usual (non-gravitational, non-conformal) quantum field theory.
Consider a non-gravitational quantum field theory in which asymptotic states contain a single species of particles described by creation/annihilation operators \(a^{\dagger}_{\mathbf{p},s}\)/a p,s , where p and s are the momentum and spin indices, respectively. The Hilbert space of the theory is then (isomorphic to) the Fock space

where  represents the n-particle Hilbert space given by
represents the n-particle Hilbert space given by  ,
,  ,
,  , … . With generic interactions, a state in
, … . With generic interactions, a state in  in Eq. (29) evolves across different components
in Eq. (29) evolves across different components  , i.e., the time evolution operator allows for a process changing the particle number. For example, in the Standard Model, collision of an electron and a positron having well-defined momenta/spins at t=−∞ leads to
, i.e., the time evolution operator allows for a process changing the particle number. For example, in the Standard Model, collision of an electron and a positron having well-defined momenta/spins at t=−∞ leads to
where we have expanded the state Ψ(t) in terms of the Fock-space states, which is appropriate for t→±∞ when interactions are weak. Note that Eq. (30) should not be interpreted that the initial e + e − state evolves probabilistically into different states |e + e −〉, |μ + μ −〉, and so on. According to the laws of quantum mechanics, the evolution of the state Ψ(t) is deterministic—it simply evolves into a unique state Ψ(t=+∞) which contains components |e + e −〉,|μ + μ −〉,… when expanded in Fock-space states.
The situation in quantum gravity is analogous. We first need to fix the Hilbert space basis to discuss states unambiguously. We assume that, with a fixed local Lorentz frame associated with a fixed reference point p, we have a set of local operators at low energies; specifically, we have a set of quantum fields ϕ i (x) defined on the past light cone of p. This can provide “meaning” to the states according to the responses to these field operators, and we can now construct states using the language of, e.g., spacetime points.
Let us consider Hilbert space  corresponding to a set of fixed semi-classical geometries
corresponding to a set of fixed semi-classical geometries  , which are defined on the past light cone of p and have the same (stretched) apparent horizon
, which are defined on the past light cone of p and have the same (stretched) apparent horizon  (in the sense that they lead to the same internal geometry of ∂M). Note that if
(in the sense that they lead to the same internal geometry of ∂M). Note that if  is d−2 dimensional, the corresponding
is d−2 dimensional, the corresponding  ’s (which are then d−1 dimensional) represent d dimensional spacetime. As discussed before, the states are defined on the past light cone bounded by the horizon; specifically, the states on these geometries form Hilbert space
’s (which are then d−1 dimensional) represent d dimensional spacetime. As discussed before, the states are defined on the past light cone bounded by the horizon; specifically, the states on these geometries form Hilbert space

where  and
and  represent Hilbert space factors associated with the degrees of freedom inside and on
represent Hilbert space factors associated with the degrees of freedom inside and on  , respectively. What do we know about
, respectively. What do we know about  and
and  ? The covariant entropy bound [48, 49] suggests that the dimension of
? The covariant entropy bound [48, 49] suggests that the dimension of  is
is  , where
, where  is the area of the horizon
is the area of the horizon  in Planck units, and the standard horizon entropy implies that the dimension of
in Planck units, and the standard horizon entropy implies that the dimension of  is the same, so
is the same, so

The fact that the maximum number of degrees of freedom (i.e. the logarithm of the dimension of the Hilbert space) scales with the area, rather than the volume, is a manifestation of the holographic principle.
Analogously to the case of non-gravitational quantum field theory, Eq. (29), the full Hilbert space of dynamical spacetime is (isomorphic to) the direct sum of the Hilbert spaces for different  ’s:
’s:

so that  . Note that the dimension here includes that of “matter” degrees of freedom, i.e. excitations associated with the quantum fields ϕ
i
(x). We emphasize that defining the states in
. Note that the dimension here includes that of “matter” degrees of freedom, i.e. excitations associated with the quantum fields ϕ
i
(x). We emphasize that defining the states in  need not require a fixed background space a priori; rather, in a more complete framework, spacetime interpretation of the states would arise as a result of the algebra of quantum field operators, ϕ
i
(x), and the responses of the states to these operators.
need not require a fixed background space a priori; rather, in a more complete framework, spacetime interpretation of the states would arise as a result of the algebra of quantum field operators, ϕ
i
(x), and the responses of the states to these operators.
The general evolution of a state in dynamical spacetime is assumed to be unitary in the full Hilbert space  in Eq. (33), but not in each
in Eq. (33), but not in each  . Unitarity of the evolution is a hypothesis of the framework. Its consistency was discussed in Ref. [14]. In particular, since the full information contained on the past light cone outside the horizon (in the sense of the conventional global spacetime picture) can be encoded on the horizon due to the covariant entropy bound, we can have enough degrees of freedom on the horizon that can determine the future evolution of the state as in conventional null quantization in global spacetime; namely, the evolution inside the horizon can be equivalent to the standard time evolution.
. Unitarity of the evolution is a hypothesis of the framework. Its consistency was discussed in Ref. [14]. In particular, since the full information contained on the past light cone outside the horizon (in the sense of the conventional global spacetime picture) can be encoded on the horizon due to the covariant entropy bound, we can have enough degrees of freedom on the horizon that can determine the future evolution of the state as in conventional null quantization in global spacetime; namely, the evolution inside the horizon can be equivalent to the standard time evolution.
In Fig. 1, we show the evolution of a state in some cosmological spacetimes for illustrative purposes. In general, however, the evolution leads to a state that is a superposition of components states representing well-defined spacetimes, hence leading to the multiverse (or quantum many worlds) picture:
where |Σ〉 is an initial state at t=t
0, e.g. an eternally inflating state in  , while the sum in the final state Ψ(t) runs over states in different
, while the sum in the final state Ψ(t) runs over states in different  , giving a superposition of macroscopically different worlds (universes). Quantum field theory on a fixed gravitational background corresponds to a special case in which transitions between (some of the)
, giving a superposition of macroscopically different worlds (universes). Quantum field theory on a fixed gravitational background corresponds to a special case in which transitions between (some of the)  are prohibited. This is analogous to the nonrelativistic limit of usual quantum field theory, in which transitions between different
are prohibited. This is analogous to the nonrelativistic limit of usual quantum field theory, in which transitions between different  do not occur. The underlying dynamics for gravity, however, is much more general—the time evolution operator allows for “hopping” between different components
do not occur. The underlying dynamics for gravity, however, is much more general—the time evolution operator allows for “hopping” between different components  in Eq. (33). The semi-classical evolution in which the area of the apparent horizon changes is precisely a succession of such processes.
in Eq. (33). The semi-classical evolution in which the area of the apparent horizon changes is precisely a succession of such processes.
A quantum state is defined on past light cones (45∘ lines) bounded by the “(stretched) apparent horizons” (thick solid lines). The left (right) diagram represents the evolution of a state in spacetime in which a Minkowski (anti de Sitter) bubble is nucleated in a meta-stable de Sitter vacuum. The bubble walls are depicted by dashed lines
“Reference Frame Dependence” of the Concept of Spacetime
What happens if we change the reference frame, e.g. by a spatial translation or boost? As in any symmetry transformation, this operation must be represented by a unitary transformation in Hilbert space. In particular, if we focus on histories before any component of the state hitting spacetime singularities (the effect of which will be discussed in Sect. 7), then it must be represented entirely in the Hilbert space  in Eq. (33), but not necessarily in each component
in Eq. (33), but not necessarily in each component
 . Namely, the transformation can mix elements in different
. Namely, the transformation can mix elements in different  . Moreover, even if the transformation maps all the elements in
. Moreover, even if the transformation maps all the elements in  onto themselves for some
onto themselves for some  , there is no reason that it should not mix the degrees of freedom associated with
, there is no reason that it should not mix the degrees of freedom associated with  and
and  .
.
Let us consider a state |Ψ(t)〉 that represents the entire quantum universe, which we call the multiverse state. Suppose that at some time t, the multiverse state is expanded in terms of the locality basis states |κ
m
〉 that are elements of  in Eq. (33):
in Eq. (33):

where 〈κ m |κ n 〉=δ mn . The parameter t here is introduced to describe the evolution of |Ψ(t)〉: \(| \varPsi(t_{1}) \rangle= e^{-iH(t_{1}-t_{2})} | \varPsi (t_{2}) \rangle\). A useful choice for t is the proper time at p, although any other monotonic parameterization works as well at the cost of (potentially) making the explicit form of H complicated.
In d spacetime dimensions, a change of the reference frame can be specified by d(d+1)/2 parameters {r
i
,η
i
,θ
[ij],t}: d−1 spatial translations r
i
, d−1 boosts η
i
, and (d−1)(d−2)/2 rotations θ
[ij], performed at time t, where i=1,…,d−1. These correspond to the freedom in electing a local inertial frame in spacetime, from which we view the system. Let us consider the Hilbert (sub)space corresponding to de Sitter space: Eq. (28) where  and
and  . Consider a state in this space represented as
. Consider a state in this space represented as
at time t, where |excited〉inside implies that there is an object within the horizon, and |0〉horizon is (one of) the ground state(s) for the horizon degrees of freedom. If we change the reference frame by performing a large spatial translation (larger than the Hubble radius) at this time, then the state transforms as
where |0〉inside represents (one of) the vacuum state(s) within the horizon, and |excited〉horizon an excited state for the horizon degrees of freedom. This provides a simple example in which degrees of freedom in the bulk and on the horizon are mixed under a change of the reference frame.
A more drastic situation may occur when there is a black hole. Consider a state |ϕ〉 in  at time t, where
at time t, where  is a spacetime containing a black hole but with the reference point p staying outside the horizon, i.e.
is a spacetime containing a black hole but with the reference point p staying outside the horizon, i.e.  in Eq. (26):
in Eq. (26):

Now, suppose we evolve the state |ϕ〉 back in time to an early time t
0, perform a boost so that p crosses the horizon at some time between t
0 and t, and then evolve |ϕ〉 forward in time to the same t. Under this reference frame change, |ϕ〉 is transformed into a state that is not in  but in
but in  in Eq. (27):
in Eq. (27):

so that the degrees of freedom associated with the horizon,  , are mapped into those with the inside spacetime,
, are mapped into those with the inside spacetime,  , which did not exist in the
, which did not exist in the
 containing |ϕ〉 before the transformation. This mapping should be one-to-one if U
B
is unitary, which is possible because the holographic principle ensures
containing |ϕ〉 before the transformation. This mapping should be one-to-one if U
B
is unitary, which is possible because the holographic principle ensures  . (Here, we have assumed that the time t is before p hits the singularity in the boosted frame.) Note that both
. (Here, we have assumed that the time t is before p hits the singularity in the boosted frame.) Note that both  and
and  are contained in the full Hilbert space
are contained in the full Hilbert space  as separate components:
as separate components:  , since
, since  contains all the possible semi-classical geometries as viewed from a local Lorentz frame of p. Thus the transformation at t corresponding to the reference frame change B at t
0 is represented within
contains all the possible semi-classical geometries as viewed from a local Lorentz frame of p. Thus the transformation at t corresponding to the reference frame change B at t
0 is represented within  , as it should be.
, as it should be.
The statement in Eq. (39) is nothing but black hole complementarity. Black hole complementarity (or more generally, horizon complementarity) arises because changes of the reference frame are represented in the Hilbert space of Eq. (33), which contains components  that are defined only in restricted spacetime regions because of the existence of horizons. In general, these changes transform degrees of freedom associated with spacetime to those with a horizon, or vice versa—the concept of spacetime depends on the reference frame.
that are defined only in restricted spacetime regions because of the existence of horizons. In general, these changes transform degrees of freedom associated with spacetime to those with a horizon, or vice versa—the concept of spacetime depends on the reference frame.
The transformation discussed here is supposed to be consistent with the global spacetime picture of general relativity. Under current theoretical technology, we may view this as a sort of “corresponding principle”—understanding the precise mathematical structure of the transformation law would require the (yet unknown) fundamental theory. The transformation can also be viewed as an extension of the Poincaré transformation in the quantum gravitational context. For a given t, the transformation here is specified by (d−1)(d+2)/2 parameters: r i ,η i ,θ [ij]. In the limit G N →0, where relative accelerations between all families of geodesics vanish, the transformation is reduced to an element of the (d−1)(d+2)/2 parameter subset of standard Poincaré transformations consisting of spatial translations, rotations and boosts. Time translation also arises from invariance under a shift of the origin of t in the proper time parameterization. The set of these transformations, therefore, is reduced to the standard Poincaré transformations in the limit G N →0.
This is very much analogous to the fact that the standard Lorentz transformation is reduced to the Galilean transformation in the limit c→∞, where c is the speed of light. In the Galilean transformation a change of the reference frame leads only to a constant shift of all the velocities, while in the Lorentz transformation it also alters temporal and spatial lengths (time dilation and Lorentz contraction) and makes the concept of simultaneity relative. With gravity, a change of the reference frame makes even the concept of spacetime relative. The trend is consistent—as we “turn on” fundamental constants in nature (c=∞→finite and G N =0→finite), physics becomes more and more “relative,” i.e. the description of the same physical system from different reference frames differ more. The transformations described here (together with time translation) provide the extension of the Galilean group with c, G N , and ħ all finite.
7 Hilbert Space for Quantum Gravity
Here we discuss the full Hilbert space for quantum gravity. We argue that it contains an infinite number of “intrinsically quantum mechanical” states associated with spacetime singularities, which do not admit any classical interpretation. It is in this full Hilbert space in which the evolution of the multiverse state is unitary and an arbitrary reference frame change is represented as a unitary transformation.
Meaning of Spacetime Singularities
What happens if a component of Eq. (35) hits a spacetime singularity at some time t s ? We conjecture that it should be dropped from physical considerations after time t s . This is motivated by the following independent arguments [14]:
-
The covariant entropy bound does not count the degrees of freedom that have hit a singularity. Imagine sending a light sheet inwards from a black hole horizon H. The degrees of freedom swiped by the light sheet are then bounded by the area of the horizon
 . The entropy bound, however, does not limit the amount of information that hits the singularity before being swiped by the light sheet.
. The entropy bound, however, does not limit the amount of information that hits the singularity before being swiped by the light sheet. -
Super-Planckian physics does not have degrees of freedom as suggested by field theory. Consider a black hole (or de Sitter) horizon. Because of blueshift, the local temperature at the mathematical horizon formally diverges. In fact, the physical horizon, from which Hawking radiation arises, is a Planckian distance away from the mathematical horizon: the “stretched” horizon. This suggests that super-Planckian physics does not have degrees of freedom as indicated by field theory.
What does dropping from consideration mean? In Ref. [14], it was postulated that a component that hits a singularity at time t s is simply eliminated from the state |Ψ(t)〉 at that time, t=t s . This, however, leads to the following paradoxical situations. What if |Ψ(t)〉 contains only components that hit singularities in the future? This must violate unitarity, and therefore so does any state containing them. Furthermore, even if we accepted unitarity violation, systems having only de Sitter and anti de Sitter vacua would allow for (a constant fraction of) |Ψ(t)〉 to stay in a de Sitter phase at t→∞, since components tunneled into the anti de Sitter vacuum keep disappearing. This is extremely counter-intuitive.
We are therefore led to the following picture. The components that hit spacetime singularities keep existing in |Ψ(t)〉, but they are no longer extracted by projection operators  or
or  appearing in the probability formula because these states cannot be interpreted as those associated with (semi-)classical spacetime. This implies that the full Hilbert space for quantum gravity must contain these “intrinsically quantum mechanical” states, associated with singularities:
appearing in the probability formula because these states cannot be interpreted as those associated with (semi-)classical spacetime. This implies that the full Hilbert space for quantum gravity must contain these “intrinsically quantum mechanical” states, associated with singularities:

where  is the component that allows for spacetime interpretation, Eq. (33), while
is the component that allows for spacetime interpretation, Eq. (33), while  is the one that does not. Note that the elements of
is the one that does not. Note that the elements of  represent the states when (after) the reference point p
0 hits a spacetime singularity. There may be configurations in which a spacetime singularity is located somewhere on the past light cone of p
0, but these states are all classified in
represent the states when (after) the reference point p
0 hits a spacetime singularity. There may be configurations in which a spacetime singularity is located somewhere on the past light cone of p
0, but these states are all classified in  as the usual spacetime states. Note that this treatment of “dropping” is different from simply eliminating the relevant components. For example, a de Sitter phase can now disappear by tunneling purely into an anti de Sitter vacuum.
as the usual spacetime states. Note that this treatment of “dropping” is different from simply eliminating the relevant components. For example, a de Sitter phase can now disappear by tunneling purely into an anti de Sitter vacuum.
We assume that the evolution of the multiverse state |Ψ(t)〉 is unitary in  , and that any change of the reference frame at an arbitrary time t is represented by a unitary transformation in this Hilbert space. According to the current understanding of string theory, a full quantum gravitational theory possesses many de Sitter, anti de Sitter, and Minkowski vacua. In particular, it possesses exactly supersymmetric Minkowski vacua, which are absolutely stable due to the positive energy theorem [50, 51]. This implies that the dimension of
, and that any change of the reference frame at an arbitrary time t is represented by a unitary transformation in this Hilbert space. According to the current understanding of string theory, a full quantum gravitational theory possesses many de Sitter, anti de Sitter, and Minkowski vacua. In particular, it possesses exactly supersymmetric Minkowski vacua, which are absolutely stable due to the positive energy theorem [50, 51]. This implies that the dimension of  is infinite,
is infinite,  , since the Hilbert space dimension of (stable) Minkowski space is infinite. What about
, since the Hilbert space dimension of (stable) Minkowski space is infinite. What about  ? Consider a set of states that hit singularities at some late time. In the eternally inflating multiverse, these states can be mapped into those that evolve into stable supersymmetric Minkowski states, by appropriate boost transformations. This suggests that
? Consider a set of states that hit singularities at some late time. In the eternally inflating multiverse, these states can be mapped into those that evolve into stable supersymmetric Minkowski states, by appropriate boost transformations. This suggests that  , which makes it possible that components that hit singularities do never return to states in
, which makes it possible that components that hit singularities do never return to states in  , associated with spacetime. Namely, stable Minkowski and anti de Sitter vacua can act as “sinks” in the landscape.
, associated with spacetime. Namely, stable Minkowski and anti de Sitter vacua can act as “sinks” in the landscape.
The Heat Death of the Multiverse
What is the ultimate fate of the multiverse state? Starting from a generic eternally inflating state, the coefficients of any components in unstable vacua will eventually decay. In the string landscape, we expect that all the de Sitter as well as non-supersymmetric Minkowski vacua decay into some lower energy vacua, given that there is a huge number of possible decay channels. The multiverse state, therefore, will asymptotically become a superposition of supersymmetric Minkowski and singularity states (associated with black hole and big crunch singularities). Here, supersymmetric Minkowski states mean configurations in a bubble universe on a supersymmetric Minkowski vacuum, approaching asymptotically the vacuum states as the universe expands. In fact, this is simply a consequence of the second law of thermodynamics, given that the Hilbert space dimensions of Minkowski and singularity worlds are infinite. In other words, the coarse-grained entropy of the multiverse diverges in the asymptotic future: S final≡S multiverse(t→∞)=∞—in this picture, the ultimate future of the multiverse is the “heat death.”
8 Probabilities in the Quantum Multiverse
The (Extended) Born Rule
Having understood how the state |Ψ(t)〉 is defined, the probability formula can be obtained following the earlier discussions in Sects. 2–4. An important new point here is that the “time” t in quantum gravity is simply an auxiliary parameter introduced to describe the “evolution” of the state—the physical information is only in correlations between events [52].
Any physical question can then be phrased as: given condition A we specify, what is the probability for an event B to occur? For example, one can specify a certain “premeasurement” situation A pre as well as a “postmeasurement” situation A post as A={A pre,A post}, and then ask the probability of a particular result B to be obtained. The information about real, physical time is included in conditions A and B through specifications of any non-static observables. The relevant probability P(B|A) is then given by

Here, \(U(t_{1},t_{2}) = e^{-iH(t_{1}-t_{2})}\) with H being the Hamiltonian for the entire system, and  is the operator projecting onto states consistent with condition X:
is the operator projecting onto states consistent with condition X:  . Note that since we have already fixed a reference frame, conditions A
pre and A
post in general must involve specifications of ranges of location and velocity for physical objects with respect to the origin of the coordinates p.
. Note that since we have already fixed a reference frame, conditions A
pre and A
post in general must involve specifications of ranges of location and velocity for physical objects with respect to the origin of the coordinates p.
Equation (41) is our final formula for the probabilities. The integrations over “time” t are taken from t=t 0, where the initial condition for |Ψ(t)〉 is specified, to t=∞, which arise because conditions A pre and A post may be satisfied at any values of t (denoted by t 1 and t 2 in the equation). This, together with appropriate transformations of H, ensures that P(B|A) is invariant under reparameterization of t, as required by general covariance. If conditions A pre and A post are selecting configurations at same t, then Eq. (41) is reduced to the formula of Eq. (1).Footnote 7
We note that the present framework does not suffer from the problem discussed in Refs. [53–55]: the ambiguity in the Born rule that arises if an observer can condition only a part of a wavefunction, which is the case in the conventional global description of the quantum universe. Since the quantum states in our framework represent only spacetime regions within the apparent horizons, all the systems included in a state can (at least in principle) be physically probed [14].
Incidentally, Eq. (41) can be straightforwardly extended to the mixed state case

where ρ(t)≡∑
i
p
i
|Ψ
i
(t)〉〈Ψ
i
(t)| (∑
i
p
i
=1) is a density matrix. This formula is also applicable for a reduced density matrix, obtained by tracing out some of the degrees of freedom, with the understanding that  act on degrees of freedom that are not traced out.
act on degrees of freedom that are not traced out.
Unification of the Eternally Inflating Multiverse and Many Worlds in Quantum Mechanics
Under the usual situation of a terrestrial experiment, the formula of Eq. (41) is reduced to the standard Born rule. This can be seen by isolating the degrees of freedom relevant to the experiment. Suppose \(O_{A_{\mathrm{pre}}}\) acts on these degrees of freedom and selects a particular premeasurement situation A
pre, which is realized in components of |Ψ(t)〉 at multiple values of \(t = \hat{t}_{i}\) (i=1,2,…): \(O_{A_{\mathrm{pre}}} U(t_{1},0) | \varPsi(0) \rangle = \sum_{i} c_{i} | \phi(\hat{t}_{i}) \rangle\otimes| \hat{\varPsi }_{i}(\hat{t}_{i}) \rangle\, \delta(t_{1}-\hat{t}_{i})\), where \(| \phi(\hat{t}_{i}) \rangle\) represents the degrees of freedom relevant to the experiment, and \(| \hat{\varPsi}_{i}(\hat{t}_{i}) \rangle\) the rest. In the limit that A
pre selects the initial experimental setup infinitely accurately, which we are considering here for simplicity, the initial state for the experiment is \(| \phi(\hat{t}_{1}) \rangle = | \phi(\hat{t}_{2}) \rangle = \cdots\equiv| \phi(t_{\mathrm{before}}) \rangle\). Then, assuming that \(O_{A_{\mathrm{post}}}\), which selects a particular postmeasurement situation, acts on the same degrees of freedom as \(O_{A_{\mathrm{pre}}}\), we obtain \(O_{A_{\mathrm{post}}} \hat{U}(t_{2},t_{\mathrm{before}}) | \phi (t_{\mathrm{before}}) \rangle \approx c | \phi(t_{\mathrm{after}}) \rangle\delta(t_{2} - t_{\mathrm{after}})\), where \(\hat{U}(t_{1},t_{2})\) is a factor in U(t
1,t
2) acting only on the experimental degrees of freedom, and t
after is the smallest value of t
2 consistent with the projection \(O_{A_{\mathrm{post}}}\). Rewriting  and
and  as
as  and
and  , respectively, Eq. (41) gives the probability of obtaining outcome α:
, respectively, Eq. (41) gives the probability of obtaining outcome α:  . This is nothing but the usual Born rule.
. This is nothing but the usual Born rule.
The formula of Eq. (41) can also be used to answer questions regarding global properties of our universe. To predict/postdict physical parameters x, for example, we need to choose A to select the situation of making a measurement of x. We can then use various different values (ranges) of x for B, to obtain the probability distribution P(x). Despite the fact that the t integrals run to ∞, the resulting P(B|A) is well-defined, since |Ψ(t)〉 is continually “diluted” into supersymmetric Minkowski and singularity states [14]. The procedure to make predictions/postdictions in this way was discussed in Ref. [28], where the probability distribution of the vacuum energy, x=ρ Λ , was computed.
It is striking that the simple, basic formalism developed here applies to physics at all scales. In particular, the single probability formula Eq. (41) can be used to answer any physical questions, given a state |Ψ(t)〉. This, therefore, provides complete unification of the eternally inflating multiverse and many worlds in quantum mechanics. These two are really the same thing—they simply refer to the same phenomenon occurring at (vastly) different scales.
9 Summary
An essential feature of quantum mechanics is that information is fragile. Quantum information cannot be faithfully duplicated—the exact identification of a single state is not possible without having a prior knowledge of the state. Moreover, quantum information transmitted through physical processes will in general become non-local, encoded in the entanglement structure of a quantum state.
Despite this intrinsically non-local nature of quantum states, however, the dynamics is local. Specifically, the time evolution operator takes a special form such that the concept of locality can be defined in spacetime. This feature allows for a limited set of information (among the full quantum information) to be copiously duplicated, i.e. “amplified,” and it is (only) this information that we can meaningfully store, compare, and handle. Because of the structure of the evolution operator, the relevant information is associated with well-defined classical configurations in phase space, at least for macroscopic systems.
In a system with gravity, the whole picture is more subtle, since if we choose wrong quantization hypersurfaces, then spacetime locality is not manifest even at distances much larger than the quantum gravity scale. We argued, however, that spacetime locality can be preserved if we define quantum states in restricted spacetime regions: in and on (stretched) apparent horizons as viewed from a local Lorentz frame of a fixed spatial point p. This can be viewed as a “unitary gauge for quantum gravity,” on which our intuition should be based. By appropriately limiting the dimensions of the Hilbert subspaces corresponding to a fixed semi-classical geometry, all the redundancies/overcountings associated with a general relativistic, global spacetime description of nature are fixed/eliminated. These include general covariance, global overcounting related to complementarity, and local overcounting implied by the holographic principle.
The need for fixing a reference frame in describing the gravitational system quantum mechanically was emphasized. We identified the transformation associated with changes of the reference frame, which is specified by d(d+1)/2 parameters in d spacetime dimensions. This transformation is the origin of horizon complementarity as well as the “observer dependence” of horizons and spacetime. The transformation is reduced to the standard Poincaré transformation in the limit G N →0, so it can naturally be regarded as an extension of the Poincaré transformation in the quantum gravitational context. This is much like that the standard Lorentz transformation is regarded as an extension of the Galilean transformation, where the former is reduced to the latter in the limit c→∞.
It is remarkable that the simple framework described in this paper is applicable to physics at all scales, from the smallest (Planck length) to the largest (multiverse). Indeed, it is quite striking that quantum mechanics does not need any modification to be applied to phenomena at such vastly different scales. Does quantum mechanics break down at some point? We don’t know. But perhaps, the beginning of the multiverse might provide one.
Notes
There are several varying, though related, definitions of the measure problem in the literature. In this paper we adopt the one as stated above, which appears, e.g., in Refs. [10–13]; namely, even if one knows the initial condition and dynamical evolution, the probability is not defined because of the infinity associated with eternally inflating spacetime; and physical predictions depend highly sensitively on how these infinities are regulated, for which there is no fundamental principle to choose one over others.
This does not mean that we cannot observe a superposition of classically different configurations. It just says that the statement “the system was in a superposition state” is already classical, and it is this information that is actually amplified.
Here we consider the apparatus (or observer) as a microscopic pure state for illustrative purposes. In practice (or perhaps even in principle), we do not know which microstate a given macroscopic configuration is in, in which case we should instead consider a density matrix in which all the microscopic information is coarse-grained. Our formalism is straightforwardly extended to this case; see e.g. Eq. (42) in Sect. 8.
It is important to realize that spacetime locality is the property of the operator algebra, and not states. In fact, a state can be easily (and, indeed, is generically) non-local, e.g., as the Bell state appearing in the Einstein-Podolsky-Rosen experiment.
Note that this would not generally be the case if the relevant object were microscopic, i.e. described by a Hilbert space with small dimensions. In that case, two different states could significantly overlap (recohere) in the future.
If the multiverse state is not generic, the Hilbert space relevant for it can be (effectively) finite dimensional; see Ref. [29].
The formula in Eq. (41) treats the state between t 1 and t 2 as that evolved from
 , not |Ψ(t
1)〉. This is justified under the current setup, i.e. a generic initial state |Ψ(t
0)〉 evolving into the heat death, but not in the case where the possibility of recoherence cannot be ignored for macroscopic objects. In such a case, the formula in Eq. (1) must be used, which applies in any quantum mechanical system (and allows for answering any physical questions in principle).
, not |Ψ(t
1)〉. This is justified under the current setup, i.e. a generic initial state |Ψ(t
0)〉 evolving into the heat death, but not in the case where the possibility of recoherence cannot be ignored for macroscopic objects. In such a case, the formula in Eq. (1) must be used, which applies in any quantum mechanical system (and allows for answering any physical questions in principle).
References
Weinberg, S.: Phys. Rev. Lett. 59, 2607 (1987)
Guth, A.H., Weinberg, E.J.: Nucl. Phys. B 212, 321 (1983)
Vilenkin, A.: Phys. Rev. D 27, 2848 (1983)
Linde, A.D.: Phys. Lett. B 175, 395 (1986)
Linde, A.D.: Mod. Phys. Lett. A 1, 81 (1986)
Bousso, R., Polchinski, J.: J. High Energy Phys. 06, 006 (2000). arXiv:hep-th/0004134
Kachru, S., Kallosh, R., Linde, A., Trivedi, S.P.: Phys. Rev. D 68, 046005 (2003). arXiv:hep-th/0301240
Susskind, L.:. arXiv:hep-th/0302219
Douglas, M.R.: J. High Energy Phys. 05, 046 (2003). arXiv:hep-th/0303194
Guth, A.H.: Phys. Rep. 333, 555 (2000). arXiv:astro-ph/0002156
Vilenkin, A.: J. Phys. A 40, 6777 (2007). arXiv:hep-th/0609193
Winitzki, S.: Lect. Notes Phys. 738, 157 (2008). arXiv:gr-qc/0612164
Linde, A.: Lect. Notes Phys. 738, 1 (2008). arXiv:0705.0164 [hep-th]
Nomura, Y.: J. High Energy Phys. 11, 063 (2011). arXiv:1104.2324 [hep-th]
’t Hooft, G.: arXiv:gr-qc/9310026
Susskind, L.: J. Math. Phys. 36, 6377 (1995). arXiv:hep-th/9409089
Bousso, R.: J. High Energy Phys. 07, 004 (1999). arXiv:hep-th/9905177
Susskind, L., Thorlacius, L., Uglum, J.: Phys. Rev. D 48, 3743 (1993). arXiv:hep-th/9306069
Susskind, L.: Phys. Rev. Lett. 71, 2367 (1993). arXiv:hep-th/9307168
Stephens, C.R., ’t Hooft, G., Whiting, B.F.: Class. Quantum Gravity 11, 621 (1994). arXiv:gr-qc/9310006
Ollivier, H., Poulin, D., Zurek, W.H.: Phys. Rev. Lett. 93, 220401 (2004). arXiv:quant-ph/0307229
Ollivier, H., Poulin, D., Zurek, W.H.: Phys. Rev. A 72, 042113 (2005). arXiv:quant-ph/0408125
Blume-Kohout, R., Zurek, W.H.: Found. Phys. 35, 1857 (2005). arXiv:quant-ph/0408147
Blume-Kohout, R., Zurek, W.H.: Phys. Rev. A 73, 062310 (2006). arXiv:quant-ph/0505031
Wootters, W.K., Zurek, W.H.: Nature 299, 802 (1982)
Everett, H. III: Rev. Mod. Phys. 29, 454 (1957)
Schlosshauer, M.: Decoherence and the Quantum-to-Classical Transition. Springer, Berlin (2007), and references therein
Larsen, G., Nomura, Y., Roberts, H.L.L.: Phys. Rev. D 84, 123512 (2011). arXiv:1107.3556 [hep-th]
Nomura, Y.: Phys. Rev. D 86, 083505 (2012). arXiv:1205.5550 [hep-th]
Bousso, R., Susskind, L.: Phys. Rev. D 85, 045007 (2012). arXiv:1105.3796 [hep-th]
Aguirre, A., Tegmark, M., Layzer, D.: arXiv:1008.1066 [quant-ph]
Tegmark, M.: Found. Phys. Lett. 9, 25 (1996). arXiv:quant-ph/9603008
Bousso, R.: Phys. Rev. Lett. 97, 191302 (2006). arXiv:hep-th/0605263
Bousso, R., Freivogel, B., Yang, I.-S.: Phys. Rev. D 74, 103516 (2006). arXiv:hep-th/0606114
Bousso, R., Freivogel, B., Yang, I.-S.: Phys. Rev. D 79, 063513 (2009). arXiv:0808.3770[hep-th]
von Neumann, J.: Mathematische Grundlagen der Quantenmechanik. Springer, Berlin (1932)
Zurek, W.H.: Phys. Rev. D 24, 1516 (1981)
Zurek, W.H.: Phys. Rev. D 26, 1862 (1982)
Zeh, H.D.: Found. Phys. 1, 69 (1970)
Weinberg, S.: The Quantum Theory of Fields, vol I. Cambridge University Press, Cambridge (1995)
Aguirre, A., Carroll, S.M., Johnson, M.C.: arXiv:1108.0417 [hep-th]
Dyson, L., Kleban, M., Susskind, L.: J. High Energy Phys. 10, 011 (2002). arXiv:hep-th/0208013
Susskind, L., Lindesay, J.: An Introduction to Black Holes, Information and the String Theory Revolution: The Holographic Universe. World Scientific, Singapore (2005)
Almheiri, A., Marolf, D., Polchinski, J., Sully, J.: J. High Energy Phys. 02, 062 (2013). arXiv:1207.3123 [hep-th]
Susskind, L., Thorlacius, L.: Phys. Rev. D 49, 966 (1994). arXiv:hep-th/9308100
Hayden, P., Preskill, J.: J. High Energy Phys. 09, 120 (2007). arXiv:0708.4025 [hep-th]
Nomura, Y., Varela, J., Weinberg, S.J.: arXiv:1304.0448 [hep-th]
Bousso, R.: J. High Energy Phys. 06, 028 (1999). arXiv:hep-th/9906022
Bousso, R.: Rev. Mod. Phys. 74, 825 (2002). arXiv:hep-th/0203101
Weinberg, S.: Phys. Rev. Lett. 48, 1776 (1982)
Deser, S., Teitelboim, C.: Phys. Rev. Lett. 39, 249 (1977)
DeWitt, B.S.: Phys. Rev. 160, 1113 (1967)
Page, D.N.: J. Cosmol. Astropart. Phys. 07, 008 (2009). arXiv:0903.4888 [hep-th]
Page, D.N.: arXiv:0907.4152 [hep-th]
Page, D.N.: arXiv:1003.2419 [hep-th]
Acknowledgements
I am grateful for useful discussions with Alan Guth, Grant Larsen, and I-Sheng Yang. This work was supported in part by the Director, Office of Science, Office of High Energy and Nuclear Physics, of the US Department of Energy under Contract DE-AC02-05CH11231, and in part by the National Science Foundation under grant PHY-0855653.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Nomura, Y. Quantum Mechanics, Spacetime Locality, and Gravity. Found Phys 43, 978–1007 (2013). https://doi.org/10.1007/s10701-013-9729-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10701-013-9729-1


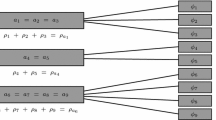



 . The entropy bound, however, does not limit the amount of information that hits the singularity before being swiped by the light sheet.
. The entropy bound, however, does not limit the amount of information that hits the singularity before being swiped by the light sheet. , not |Ψ(t
1)〉. This is justified under the current setup, i.e. a generic initial state |Ψ(t
0)〉 evolving into the heat death, but not in the case where the possibility of recoherence cannot be ignored for macroscopic objects. In such a case, the formula in Eq. (
, not |Ψ(t
1)〉. This is justified under the current setup, i.e. a generic initial state |Ψ(t
0)〉 evolving into the heat death, but not in the case where the possibility of recoherence cannot be ignored for macroscopic objects. In such a case, the formula in Eq. (