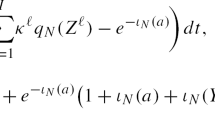Horizon dependence of utility optimizers in incomplete models

Abstract

This paper studies the utility maximization problem with changing time horizons in the incomplete Brownian setting. We first show that the primal value function and the optimal terminal wealth are continuous with respect to the time horizon T. Secondly, we exemplify that the expected utility stemming from applying the T-horizon optimizer on a shorter time horizon S<T may fail to converge to the T-horizon value as S↑T. Finally, we provide necessary and sufficient conditions preventing the existence of this phenomenon.

Appendix: Proofs

This appendix contains all the proofs. Since the proof of Theorem 4.1 is construction-based, we present it first. We then extend the duality theory of [19] to include nonnegative stochastic interest rates before proceeding with the remaining proofs. The results related to stochastic exponentials being true martingales (Example 3.2 and Lemma 4.7) are provided at the very end.

1.1 A.1 Proof of Theorem 4.1

We let (t _n ) _n∈ℕ⊆(0,1) be an increasing sequence of numbers converging to 1 and define the disjoint partition (A _n ) _n∈ℕ of Ω (up to a ℙ-null set) by

and so on. We note that by the independence of Brownian increments, we have ℙ(A _k )=1/2^k for k∈ℕ. The sequence of random variables (Y _k ) _k∈ℕ is defined by

The constants are assumed to satisfy a _k ∈(0,1) and b _k >1, whereas α _k is chosen such that $\mathbb {E}[Y_{k}] =1$ for k∈ℕ. We note that Y _k is a positive $\mathcal {F}_{t_{k+1}}$-measurable random variable which is independent of $\mathcal {F}_{t_{k}}$ for k∈ℕ. We can then define the strictly positive Lévy martingale by

$$\xi_t := \mathbb {E}\Biggl[\sum_{k=1}^\infty Y_k1_{A_k} \Bigg|\mathcal {F}_t \Biggr],\quad t\in[0,T].$$

In what follows, U denotes a utility function satisfying (4.2). The proof is finished by showing how we can use ξ to construct a complete financial market such that

$$\lim_{K\uparrow T} u^{(T)}(K,x) = -\infty,\quad u^{(T)}(x) \in \mathbb {R}, \ x>0,$$

for a specific choice of the sequences (a _k ) _k∈ℕ and (b _k ) _k∈ℕ.

By the martingale representation theorem for the Brownian motion B, we can find an adapted measurable process $\lambda\in \mathcal {L}^{2}$ such that

$$d\xi_t = -\xi_t \lambda_t \,dB_t, \quad t\in(0,1), \qquad \xi_0 =1.$$

By defining the drift process μ _t :=λ _t , the volatility process σ _t :=1 and the interest rate r _t :=0, we see that ξ is the density process Z ^λ defined by (2.3) and consequently Assumption 2.1 is satisfied.

To construct the two sequences (a _k ) _k∈ℕ and (b _k ) _k∈ℕ, we first observe that

where we have defined the $\mathcal {F}_{n}$-measurable set C _n by

$$C_n:= (B_{t_1}\ge0) \cap(B_{t_2}-B_{t_1}\ge0) \cap\cdots\cap (B_{t_k}-B_{t_{k-1}} \ge0) =\Biggl(\,\bigcup _{k=1}^n A_k\Biggr)^c.$$

By Tonelli’s theorem for conditional expectations, we have the relation

$$\xi_{t_n} = \sum_{k=1}^\infty \mathbb {E}[Y_k1_{A_k}|\mathcal {F}_{t_n}] = \sum_{k=1}^{n-1} Y_k1_{A_k}+1_{A_n} + 1_{C_n}.$$

By using the martingale method for complete Brownian-based models, see [4, 14], we know that the optimal terminal wealth with time horizon T:=1 satisfies

$$X^{(1)}_1 = I(y\xi_1),\quad\hbox{where} \ I(b) := \bigl(U'\bigr)^{-1}(b), \ b>0.$$

Here the Lagrange multiplier y>0 is given by the investor’s budget restriction, i.e., y satisfies $x = \mathbb {E}[\xi_{1} I(y\xi_{1})]$ where x>0 is the investor’s initial wealth. We focus on the initial wealth x ₀ such that y=1. We know that X ⁽¹⁾ ξ is a martingale on [0,1] and therefore

$$X_{t_n}^{(1)} = \frac{\mathbb {E}[X_1^{(1)}\xi_1|\mathcal {F}_{t_n}]}{\xi_{t_n}}= \frac{\mathbb {E}[I(\xi_1)\xi_1|\mathcal {F}_{t_n}]}{\xi_{t_n}},\quad n \in \mathbb {N}.$$

Similarly to the above calculations, we can compute the numerator to be

We can then compute u ⁽¹⁾(t _n ,x ₀) for n∈ℕ to be

On the other hand, u ⁽¹⁾(x ₀) is given by

$$\mathbb {E}\bigl[U\bigl(X^{(1)}_1\bigr) \bigr] = \mathbb {E}\bigl[U\bigl(I(\xi_1) \bigr) \bigr] = \sum_{k=1}^\infty \mathbb {E}\bigl[U \bigl(I(Y_k) \bigr) \bigr] \mathbb {P}(A_k).$$

The goal is therefore to construct (a _k ) _k∈ℕ and (b _k ) _k∈ℕ such that

$$\lim_{k\to\infty} \mathbb {E}\bigl[Y_kI(Y_k)\bigr] = 0\quad\hbox{and}\quad \lim_{k\to \infty}U \bigl(\mathbb {E}\bigl[Y_kI(Y_k)\bigr] \bigr)\mathbb {P}(A_k)= -\infty.$$

Provided this can be done, we should also find that $\sum_{k=n+1}^{\infty} \mathbb {E}[I(Y_{k})Y_{k}]\frac{1}{2^{k-n}}$ converges to zero. All in all, this construction would produce the limit

$$\lim_{n\to\infty} u^{(1)}(t_n,x_0)= -\infty,$$

whereas u ⁽¹⁾(1,x ₀)∈ℝ, and thereby conclude the proof. Since U is unbounded from below, we can find a sequence (x _k ) _k∈ℕ converging to zero such that

$$U(x_k) \mathbb {P}(A_k) = U(x_k)/2^k \to-\infty.$$

We then define (a _k ) _k∈ℕ and (b _k ) _k∈ℕ such that a _k ↓0 and a _k I(a _k )<x _k /2 (here we use (4.2)) and b _k ↑+∞ such that I(b _k )<x _k /2. To summarize, we define (α _n ) _n∈ℕ such that

$$\mathbb {E}[Y_n] = a_np_n+ b_n(1-p_n)=1,\quad p_n:= \mathbb {P}(B_{t_n+1}-B_{t_n}\le \alpha_n), \quad n\in \mathbb {N};$$

subsequently we define the density (ξ _t ) _t∈[0,1] in terms of (Y _k ) _k∈ℕ, and finally we define the initial wealth by $x_{0} := \mathbb {E}[\xi_{1}I(\xi_{1})]<\infty$. Then we have

$$\mathbb {E}\bigl[Y_kI(Y_k)\bigr] = a_kI(a_k)p_k+ b_kI(b_k) (1-p_k) \le x_k \downarrow 0\quad\hbox{as} \ k\to\infty,$$

since both p _k and b _k (1−p _k ) are less than one. The second requirement follows from the construction of (x _k ) _k∈ℕ and the increasing property of U, because

1.2 A.2 Duality

The duality-based existence result in [19] is derived under the assumption r _t =0, whereas [15] rely on a uniform boundedness condition on r as well as a smaller class of utility functions (excluding the negative power investors). This section explains how to adjust the dual approach of [19] to cover the case of nonnegative interest rates for general utility functions.

A strictly positive progressively measurable process Y, Y ₀=1, is called a supermartingale deflator if XY is a supermartingale for any admissible wealth process X. For $\nu\in \mathcal {L}^{2}$, Itô’s lemma shows that

$$ dY^\nu_t := -Y^\nu_t ( r_t \,dt + \lambda_t \,dB_t + \nu_t\,dW_t),\qquad Y^\nu_0:=1,$$

(A.1)

is a supermartingale deflator. Since r is assumed nonnegative, Y ^ν is a local supermartingale. To see that Y ^ν is a genuine supermartingale, we let (τ _n ) _n∈ℕ be a reducing sequence of stopping times. Fatou’s lemma shows

$$Y^\nu_s = \liminf_{n\to\infty} Y^\nu_{s\land\tau_n}\ge\liminf_{n\to \infty} \mathbb {E}\bigl[Y^\nu_{t\land\tau_n}\big|\mathcal {F}_s\bigr]\ge \mathbb {E}\bigl[Y^\nu_t\big| \mathcal {F}_s\bigr],$$

for $0\le s\le t\le\overline{T}$. This supermartingale property is the key ingredient in the duality approach developed in [19].

Lemma A.1

Under Assumption 2.1, for any supermartingale deflator Y, there exists $\nu\in \mathcal {L}^{2}$ such that $Y_{t}\le Y_{t}^{\nu}$, $t\in[0,\overline{T}]$, where Y ^ν is defined by (A.1).

Proof

We define the discounted price system

$$ \tilde{S}^{(0)}_t := 1, \qquad \tilde{S}_t := S_t/S^{(0)}_t,\quad t \in [0,\overline{T}],$$

(A.2)

and we denote by $\tilde{X}$ the corresponding discounted wealth process. Since Y is a supermartingale deflator, we also see that $S^{(0)}Y \tilde{X}$ is a supermartingale for any $\tilde{X}$. Proposition 3.2 in [21] produces the representation $S^{(0)}Y =D Z^{\lambda} \mathcal {E}(-\nu\cdot W)$, where Z ^λ is the minimal density (2.3), $\nu\in \mathcal {L}^{2}$ and D is a predictable, nonincreasing process with D ₀=1 and D _T >0. Therefore,

$$Y_t = D_t Z^\lambda_t \mathcal {E}(-\nu\cdot W)_t/S_t^{(0)}\le Z^\lambda_t \mathcal {E}(-\nu\cdot W)_t/S_t^{(0)} = Y_t^\nu,\quad t\in[0,\overline{T}].$$

 □

We define the two sets of $\mathcal {F}_{T}$-measurable random variables

$$ \mathcal {C}:=\bigl\{g\in \mathbb {L}^0_+(\mathbb {P}): g\le X_T, \;X_0=1\bigr\},\qquad \mathcal {D}:= \bigl\{h\in \mathbb {L}^0_+(\mathbb {P}): h\le Y^\nu_T\bigr\},$$

(A.3)

where X denotes some admissible wealth process and Y ^ν is given by (A.1). These sets generalize [19], (3.1) and (3.2) on p. 912, to the case of nonnegative interest rates. The supermartingale property of Y ^ν produces $\mathbb {E}[Y^{\nu}_{T}]\le1$, i.e., $\mathcal {D}$ defined by (A.3) is a bounded subset of $\mathbb {L}^{1}_{+}(\mathbb {P})$.

Lemma A.2

Under Assumption 2.1, the sets $\mathcal {C}$ and $\mathcal {D}$ are solid, convex and closed in probability. Furthermore, the sets are in bipolar relation, i.e., $\mathcal {D}^{\circ}= \mathcal {C}$ and $\mathcal {C}^{\circ}=\mathcal {D}$.

Proof

This result is basically Proposition 3.1 from [19] and we only mention the few needed adjustments. The solidity and convexity of $\mathcal {D}$ are clear (for the latter we can use Lemma A.1). $\mathcal {D}$’s closedness in probability follows as in [19], Lemma 4.1, since r≥0 ensures that Y ^ν is a supermartingale. Hence, the bipolar theorem for $\mathbb {L}^{0}_{+}(\mathbb {P})$ shows that $\mathcal {D}= \mathcal {D}^{\circ\circ}$. The inclusion $\mathcal {C}\subseteq \mathcal {D}^{\circ}$ is an immediate consequence of XY ^ν’s supermartingale property.

The set of equivalent martingale measures ℚ for the discounted market (A.2) is non-empty (because the minimal density Z ^λ is assumed to be a true martingale). Furthermore, the Radon–Nikodým derivative on $\mathcal {F}_{T}$ of such a measure ℚ can be written as

$$\frac{d\mathbb {Q}}{d\mathbb {P}} = \exp \biggl(\int_0^{T} r_u \,du \biggr) Y_T^\nu,$$

for some process $\nu= \nu^{\mathbb {Q}}\in \mathcal {L}^{2}$. For any $X\in \mathbb {L}^{0}_{+}(\mathbb {P})$, we define $\tilde{X} := X/S^{(0)}_{T}$ so that we have the identity $\mathbb {E}[Y^{\nu}_{T} X] = \mathbb {E}^{\mathbb {Q}}[\tilde{X}]$. Therefore, if $\mathbb {E}[Y^{\nu}_{T} X]\le1$ for all $\nu\in \mathcal {L}^{2}$, we can superreplicate $\tilde{X}$ in $(\tilde{S}^{(0)}, \tilde{S})$ by standard arguments; hence, we can superreplicate X in (S ⁽⁰⁾,S). This shows that $\mathcal {D}^{\circ}\subseteq \mathcal {C}$, implying $\mathcal {D}^{\circ}= \mathcal {C}$. Therefore, the set $\mathcal {C}$ is solid, convex, and closed in probability. By taking polars, we then see $\mathcal {C}^{\circ}= \mathcal {D}^{\circ\circ } = \mathcal {D}$ which finishes the proof. □

Based on [15], the dual value function corresponding to the primal problem (2.4) is defined by

$$ v^{(T)}(y) := \inf_{\nu\in \mathcal {L}^2} \;\mathbb {E}\bigl[V\bigl(y Y_T^\nu\bigr)\bigr],\quad y>0,$$

(A.4)

where V is the convex conjugate of the utility function U defined by

$$ V(b) := \sup_{a>0} \bigl( U(a) - ab \bigr),\quad b>0.$$

(A.5)

Since U(⋅) is nondecreasing and V(⋅) is nonincreasing, it is clear that the primal value function (2.4) and the dual value function (A.4) can also be written as

$$u^{(T)}(x) = \sup_{g\in \mathcal {C}} \;\mathbb {E}\bigl[U(xg)\bigr],\qquad v^{(T)}(y) = \inf_{h \in \mathcal {D}} \;\mathbb {E}\bigl[V(y h)\bigr],$$

for x,y>0. Furthermore, Lemma A.1 shows that including all supermartingale deflators Y in the minimizing (A.4) produces the same infimum. From (A.5), we see for any $\nu\in \mathcal {L}^{2}$ and any terminal wealth X _T that

$$V\bigl(yY^\nu_T\bigr) \ge U(X_T) + yX_TY^\nu_T,\quad \mathbb {P}\hbox{-almost surely}.$$

From this inequality, we get the standard weak duality inequality

$$ v^{(T)}(y) \ge\sup_{x>0} \bigl( u^{(T)}(x) - xy \bigr),\quad y>0.$$

(A.6)

We note that (A.6) holds irrespectively of whether or not the primal and dual value functions are finite-valued. The following result extends the main result of [19] to the case of nonnegative stochastic interest rates.

Theorem A.3

(Kramkov–Schachermayer)

Under Assumption 2.1, if u ^(T)(x)<∞ for some x>0, then for y>0, the dual minimizer $\nu^{(T)} = \nu^{(T)}(y)\in \mathcal {L}^{2}$ exists, i.e.,

$$v^{(T)}(y) = \mathbb {E}\bigl[V \bigl(y Y_T^{\nu^{(T)}} \bigr)\bigr].$$

The primal and dual value functions are continuously differentiable as well as mutual conjugates, i.e.,

(A.7)

(A.8)

The unique optimal terminal wealth X ^(T)=X ^(T)(x) exists and satisfies the relation $U'(X^{(T)}_{T}) = yY_{T}^{\nu^{(T)}}$, where y>0 is the Lagrange multiplier corresponding to the investor’s budget constraint, i.e., $\frac{\partial}{\partial x} u^{(T)}(x) =y$. Furthermore, $X^{(T)}Y^{\nu^{(T)}}$ is a uniformly integrable martingale.

Proof

The result follows from the “abstract version” in Sect. 3 of [19]. Properties (i) and (ii) in Proposition 3.1 in [19] are ensured by Lemma A.2. The last required property (iii) follows from r≥0, hence $1\in \mathcal {C}$, whereas Markov’s inequality and $\mathcal {D}\neq\emptyset$ produce the boundedness in probability of $\mathcal {C}$. □

1.3 A.3 Remaining proofs

We remark that no finiteness of the dual value function v ^(K)(y) for K=T is assumed in the following lemma.

Lemma A.4

Under Assumption 2.1, if v ^(K)(y)<∞ for all y>0 and all K∈[0,T), $T\le\overline {T}$, then we have

$$\liminf_{K\uparrow T, y\to y_0} v^{(K)}(y) \ge v^{(T)}(y_0),\quad y_0>0.$$

Proof

Thanks to the closedness of $\mathcal {D}$ established in Lemma A.2, the proof only requires minor modifications to the proof of Lemma 3.7 in [21]. □

Lemma A.5

Under Assumption 2.1, we have u ^(T)(x)=+∞ for all x>0 if and only if v ^(T)(y)=+∞ for all y>0.

Proof

If u ^(T)(x)=+∞ for all x>0, the weak duality inequality (A.6) gives us v ^(T)(y)=∞ for y>0. On the other hand, if u ^(T)(x)<+∞ for some x>0, we have by (A.8) that there exists some y ₀>0 such that v ^(T)(y ₀)<∞. □

Proof of Theorem 3.1

For x>0, we find that u ^(K)(x) is increasing in K, and as a consequence v ^(K)(y) is increasing in K, too. Therefore Lemma A.4 shows that

$$\lim_{K\uparrow T, y\to y_0} v^{(K)}(y) = v^{(T)}(y_0).$$

The proof of the first claim then follows by the conjugacy relationship (A.7), (A.8) between the primal and dual value functions; see Proposition 3.9 in [21].

For the second claim, we define the concave function

$$\overline{u}(x) := \lim_{K\uparrow T} u^{(K)}(x),\quad x>0.$$

If $\overline{u}(x)$ is finite for some—equivalently for all—x>0, we get for y>0 that

which is finite for some y ₀>0. This provides a uniform upper bound in K∈[0,T). By Lemma A.4, we therefore also have v ^(T)(y ₀)<∞, but this contradicts the conclusion of Lemma A.5. □

Proof of Theorem 3.5

Since u ^(K)(x) is increasing in K, we have that u ^(K)(x) is finite-valued, implying that also v ^(K)(y) is finite-valued for all K∈[0,T+ϵ]. We fix y>0 and define the function

$$f(\nu,K) := \mathbb {E}\bigl[V\bigl(yY^\nu_K\bigr)\bigr],\quad\nu \in \mathcal {L}^2, \ K\in[0,T+\epsilon].$$

By the above observation, f’s effective domain is non-empty. Furthermore, since Y ^ν is a nonnegative supermartingale and V is a convex nonincreasing function, we have for $0\le s\le t\le\overline {T}$ the relation

$$V\bigl(yY^\nu_s\bigr) \le V \bigl(\mathbb {E}\bigl[yY_t^\nu\big|\mathcal {F}_s\bigr] \bigr)\le \mathbb {E}\bigl[V \bigl(yY_t^\nu\bigr)\big|\mathcal {F}_s\bigr]$$

by Jensen’s inequality. Since the right-hand side is integrable for ν in f’s effective domain, V(yY ^ν) is a continuous submartingale. By Theorem 1.3.13 in [13], we therefore know that K↦f(K,ν) is right-continuous (and nondecreasing) on its effective domain. Consequently, we find the relation

$$\inf_{K>T}f(\nu,K) =\lim_{K\downarrow T}f(\nu,K) = f(\nu,T)$$

on f’s effective domain. Since v ^(K)(y) is also nondecreasing in K, we have

This shows the right-continuity of the dual value function, which combined with Theorem 3.1 (first part) gives us the continuity property of v ^(K)(y). Having established the continuity of the dual value function v ^(K)(y), we can prove that the primal value function shares the same continuity property; see Proposition 3.9 in [21]. The procedure used in Lemma 3.6 in [19] and Lemma 3.10 in [21] subsequently shows the continuity (in probability) of the optimal terminal wealths $X^{(K)}_{K}$, K∈[0,T+ϵ]. □

Proof of Theorem 4.2

Since u ^(T)(x)<∞, Theorem A.3 produces the primal optimizer X ^(T), the dual optimizer $Y^{\nu^{(T)}}$ and their relation

$$X^{(T)}_t =\frac{\mathbb {E}[Y^{\nu^{(T)}}_TI(yY^{\nu^{(T)}}_T)|\mathcal {F}_t]}{Y^{\nu^{(T)}}_t},\quad t\in[0,T].$$

In this expression, y>0 denotes the Lagrange multiplier corresponding to the budget restriction related to the investor’s initial wealth x>0, i.e., y is implicitly given by $x = \mathbb {E}[Y^{\nu^{(T)}}_{T}I(yY^{\nu ^{(T)}}_{T})]$. From the first part of (4.3)—or equivalently the first part of (4.4)—we can find ϵ>0 such that bI(b)≥ϵ for all b>0. This implies that we have the lower bound

$$X^{(T)}_t \ge\frac{\epsilon}{yY^{\nu^{(T)}}_t},\quad t\in[0,T].$$

By the second part of (4.3) and U(0)=−∞, we can use Lemma A.6 below to get

$$\limsup_{a\downarrow0} \; \frac{U(a)}{\log a} <+\infty.$$

This means that we can find a ₀∈(0,1) and M<∞ such that U(a)/loga<M for all a≤a ₀. As a consequence, we have

$$ U^- \bigl(X^{(T)}_t \bigr) \le U^-\bigl(\epsilon/{yY^{\nu^{(T)}}_t} \bigr) \le M\log^- \bigl(\epsilon/yY^{\nu^{(T)}}_t \bigr) + D,$$

(A.9)

where D>0 is some constant. To see that the right-hand side of (A.9) is uniformly integrable, we define the uniform integrability test function ϕ(a):=ϵe ^a/y for a∈ℝ. Then we have

which is uniformly bounded for t∈[0,T]. The uniform integrability then follows from the de la Vallée–Poussin criterion. This feature combined with Fatou’s lemma applied to the positive parts $U^{+}(X^{(T)}_{t})$ gives us

$$\liminf_{t\uparrow T} u^{(T)}(t,x) = \liminf_{t\uparrow T} \mathbb {E}\bigl[U\bigl(X^{(T)}_t\bigr)\bigr] \ge \mathbb {E}\bigl[U\bigl(X^{(T)}_T\bigr)\bigr] = u^{(T)}(x),$$

by the path continuity of (S ⁽⁰⁾,S). The opposite inequality follows from (4.1). □

Lemma A.6

Let f,g:(0,∞)→ℝ be two strictly increasing and continuously differentiable functions satisfying

$$\lim_{a\downarrow0} f(a) = \lim_{a\downarrow0} g(a)= -\infty ,\qquad \limsup_{a \downarrow0} \frac{f'(a)}{g'(a)} < +\infty.$$

Then we have

$$\limsup_{a \downarrow0}\; \frac{f(a)}{g(a)} < +\infty.$$

Proof

By assumption, we can find a ₀∈(0,∞) such that f′(a)/g′(a) is uniformly bounded for a∈(0,a ₀). Therefore, (f(a ₀)−f(a))/(g(a ₀)−g(a)) is bounded for a sufficiently small. The formula

$$\frac{f(a)}{g(a)} = \frac{f(a_0) - f(a)}{g(a_0)-g(a)} \frac {f(a)}{f(a)-f(a_0)} \frac{g(a)-g(a_0)}{g(a)}$$

together with l’Hopital’s rule applied to the last two terms on the right-hand side produces the claim. □

Lemma A.7

Under Assumption 2.1 and if u ^(T)(x)<∞ for some x>0 and $T\in[0,\overline{T}]$, the process

$$\frac{1}{\mathcal {E}(-\nu^{(T)} \cdot W)_t}\mathbb {E}\bigl[ Y^{\nu^{(T)}}_T I \bigl(yY^{\nu ^{(T)}}_T \bigr) \big|\mathcal {F}_t \bigr],\quad t\in[0,T],$$

is a supermartingale, where ν ^(T) denotes the optimal dual element and y the Lagrange multiplier corresponding to the investor’s budget constraint.

Proof

Since u ^(T)(x)<∞, the dual optimizer ν ^(T) exists by Theorem A.3, and we have the martingale representation

$$X^{(T)}_t Z^\lambda_t \mathcal {E}\bigl(-\nu^{(T)}\cdot W\bigr)_t/S^{(0)}_t =Y^{\nu ^{(T)}}_tX^{(T)}_t = \mathbb {E}\bigl[Y^{\nu^{(T)}}_T I \bigl(yY^{\nu^{(T)}}_T \bigr)\big| \mathcal {F}_t \bigr].$$

Itô’s lemma ensures that X ^(T) Z ^λ/S ⁽⁰⁾ is a local martingale which by nonnegativity is also a supermartingale. Dividing through produces the result. □

Proof of Theorem 4.3

Since U is negative, the dual minimizer ν ^(T) exists by Theorem A.3. The proof is finished by showing that (4.5) ensures uniform integrability of the family $\{(X_{t}^{(T)})^{p}\}_{t\in [T-\epsilon,T]}$. The inverse of U′ is given by I(b)=b ^1/(p−1), b>0. Let y>0 be the Lagrange multiplier corresponding to the investor’s budget constraint. The optimal wealth process $X_{t}^{(T)}$ satisfies for t∈[0,T] that

where the inequality follows by the supermartingale property proved in Lemma A.7. We define the negative constant

$$p' := \frac{1}{1/\gamma+ 1/(p-1)} \in(p-1,p).$$

Thanks to the de la Vallée–Poussin criterion, it suffices to show that the family $\{(X_{t}^{(T)})^{p'}\}_{t\in[T-\epsilon,T]}$ is uniformly bounded in $\mathbb {L}^{1}(\mathbb {P})$. Since p′<0, the above inequality gives us ℙ-a.s. for t∈[T−ϵ,T] the estimate

where the second inequality follows from Jensen’s inequality. We define conjugate exponents

$$q := \frac{p-1}{p'} >1,\qquad q' := \frac{q}{q-1} =\frac{p-1}{p-1-p'} =\frac{\gamma}{p'}$$

by the definition of p′. These exponents together with Hölder’s inequality give us

The supermartingale property of $Y^{\nu^{(T)}}$ yields $\mathbb {E}[Y^{\nu ^{(T)}}]\le1$, ensuring the validity of the last inequality. The right-hand side is uniformly bounded by (4.5). □

Proof of Corollary 4.4

We use the same notation as in the previous proof. We first show that (4.5) ensures uniform integrability of the negative parts $\{U^{-}(X_{t}^{(T)})\}_{t\in[T-\epsilon,T]}$. Condition (4.6) ensures that we can find $\overline{x}>0$ and $0<\underline{M}\le \overline{M}<\infty$ such that

$$ \underline{M} a^{p-1} \le U'(a) \le\overline{M}a^{p-1}\quad\hbox{for all}\ a\in(0,\overline{x}].$$

(A.10)

By integrating, we therefore see that U(a) is bounded from below by an affine function of a ^p for small values of a. In particular, we can find positive constants C ₁ and C ₂ such that U ⁻(a)≤C ₁ a ^p+C ₂ for all a>0. By the de la Vallée–Poussin criterion, uniform integrability follows if we can find δ>0 such that the family $\{U^{-}(X_{t}^{(T)})\}_{t\in[T-\epsilon,T]}$ is uniformly bounded in $\mathbb {L}^{1+\delta}(\mathbb {P})$. We proceed as in the previous proof. The supermartingale property established in Lemma A.7 and Jensen’s inequality (p<0) give us for t∈[T−ϵ,T] that

where C ₃,C ₄ are constants. The lower bound in (A.10) gives us

$$I(b) \ge \biggl(\frac{b}{\underline{M}} \biggr)^{1/(p-1)} \quad\hbox{for all }\ b\ge\underline{M}\overline{x}^{p-1}.$$

Since p is negative, we have ℙ-a.s. the upper bound

$$\bigl(I \bigl(yY^{\nu^{(T)}}_T \bigr) \bigr)^{p(1+\delta)} \le \bigl(I\bigl(\underline{M}\overline{x}^{p-1}\bigr) \bigr)^{p(1+\delta)}+ \underline {M}^{p(1+\delta)/(1-p)} \bigl(yY^{\nu^{(T)}}_T\bigr)^{p(1+\delta)/(p-1)}.$$

By combining these two estimates, we see that $\mathbb {E}[(U^{-}(X_{t}^{(T)}))^{1+\delta}]$ is bounded from above by

where C ₅,C ₆ are constants. These terms are uniformly bounded in t, t∈[T−ϵ,T], by the same reasoning as in the previous proof. To conclude the proof, we apply Fatou’s lemma on the positive parts to see that

whereas the opposite inequality follows from (4.1). □

Proof of Lemma 4.5

Let t∈[T−m,T] for some m>0. We have the chain of inequalities

The first inequality follows from the Cauchy–Schwarz inequality, the second by the supermartingale property of the stochastic exponential, and Jensen’s inequality gives us the final estimate. To finish the proof, we choose m small enough so that we have m(2γ ²−γ)≤δ−m2γ≤δ, and m≤ϵ (recall γ<0). Then the result follows since a continuous function on a compact interval is uniformly bounded. □

1.4 A.4 On Example 3.2 and Lemma 4.7

The following proofs are based on an iterative technique presented in [22], Sect. 6.2.

Proof of Lemma 3.3

Since μ is an OU process, we have $\mu_{t} \sim\mathcal{N} (\hbox{mean}(t),\operatorname {var}(t))$ for mean and variance functions

$$\hbox{mean}(t):= e^{-\kappa t}\mu_0 + \theta \bigl(1-e^{-\kappa t}\bigr),\qquad \operatorname {var}(t):= \beta^2\bigl(1-e^{-2\kappa t}\bigr)/2\kappa, \quad t\ge0.$$

Let us first verify that the exponential local martingale Z ^λ=Z ^μ defined by (2.3) indeed is a true martingale; see Assumption 2.1. We consider a finite partition with $\varDelta = \varDelta _{n} := \overline{T}/n$ for some n∈ℕ and some $\overline{T}>0$. By Tonelli’s theorem and Jensen’s inequality, we have

$$\mathbb {E}\bigl[e^{\frac{1}{2} \int_{i\varDelta }^{(i+1)\varDelta } \mu_t^2\,dt} \bigr]\le \frac{1}{\varDelta }\int_{i\varDelta }^{(i+1)\varDelta } \mathbb {E}\bigl[e^{\frac{1}{2} \varDelta \mu_t^2} \bigr]\,dt.$$

The inner expectation is finite whenever n is so large that $v(t)< n/\overline{T}$. This is ensured by choosing $n\ge\overline{T}\beta^{2}/2\kappa$. Consequently, Novikov’s condition is valid on each subinterval, which combined with iterative expectations gives us

$$\mathbb {E}\bigl[Z^\mu_{\overline{T}} \bigr] = \mathbb {E}\bigl[\mathbb {E}\bigl[Z^\mu_{\overline{T}}\big|\mathcal {F}_{\overline{T}-\varDelta }\bigr] \bigr] =\mathbb {E}\bigl[Z^\mu_{\overline{T}-\varDelta } \bigr] =\cdots=1.$$

Since this holds for any $\overline{T}>0$, the true martingale property of Z ^μ on [0,∞) follows.

We then consider the coupled system of ODEs

(A.11)

For κ>0 sufficiently small, the Riccati equation (A.11) has a well-defined (finite) solution up to some finite explosion time T∈(0,∞). Specifically, since p∈(0,1), we can choose κ>0 so small that the discriminant

$$4 \biggl(\kappa+\frac{\beta p}{p-1} \biggr)^2 - 4\frac{\beta^2 p}{(p-1)^2}$$

is negative. We then obtain the tangent solution presented in the appendix of [16] which explodes continuously at some positive finite time T∈(0,∞). Consequently, the entire ODE system for (a,b,c) has well defined finite solutions up to this explosion time T. For 0≤t≤K<T, we can then define the process

$$M_t := Z_t^{p/(p-1)}\exp \bigl(a(K-t) + b(K-t)\mu_t + c(K-t)\mu_t^2/2 \bigr).$$

Itô’s lemma produces the local martingale dynamics

$$dM_t = M_t \bigl( b(K-t)\beta+ \mu_t\bigl(c(K-t)\beta-p/(p-1) \bigr) \bigr)\,dB_t.$$

Since both b(⋅) and c(⋅) are uniformly bounded on [0,K], K<T, the above localization argument also produces the true martingale property of M _t , t∈[0,K]. Consequently, we obtain via the initial conditions for (a,b,c) the representation

$$E(K) := \mathbb {E}\bigl[ Z_K^{p/(p-1)} \bigr]=\exp \bigl(a(K) + b(K)\mu_0 + c(K)\mu_0^2/2 \bigr), \quad K<T.$$

Since the Riccati equation (A.11) explodes continuously to +∞ as K↑T, this representation shows that lim _K↑T E(K)=+∞. □

Proof of Lemma 3.4

The following duality argument is standard. For U(a):=a ^p/p, we have $V(b) =\frac{1-p}{p}b^{p/(p-1)}$. Let X _K be the terminal value of some admissible strategy. Then (A.5) gives us for K∈[0,T) that

where the last equality follows from $X^{(K)}_{K} = I(yZ_{K}^{\mu})$ and

$$V(b) := \inf_{a\ge0} \bigl\{ U(a) -ab \bigr\} = U \bigl(I(b) \bigr) -bI(b),\quad b>0.$$

Finally, we note that all expectations appearing in this proof are finite by Lemma 3.3 if κ>0 is small enough. □

Proof of Lemma 4.7

We first verify that Z ^λ satisfies Assumption 2.1. Since C ₁>0 and v _t is non-centrally χ ²-distributed, Novikov’s condition is satisfied locally in the sense that we can find Δ>0 such that for n∈ℕ, we have

$$\mathbb {E}\biggl[\exp \biggl(\frac{1}{2}\int_{n\varDelta }^{(n+1)\varDelta } \lambda^2_u\,du \biggr) \biggr]\le C\mathbb {E}\biggl[\exp \biggl(\int_{n\varDelta }^{(n+1)\varDelta } C_2(C_3+v_u)\,du \biggr) \biggr] <\infty,$$

where C>0 is some constant. Minor modifications of the iterative argument in the proof of Lemma 3.3 show the global martingale property of Z ^λ. This also verifies the condition of Lemma 4.5. □