Determine In-Situ Stress and Characterize Complex Fractures in Naturally Fractured Reservoirs from Diagnostic Fracture Injection Tests

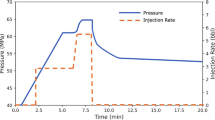
Abstract

Estimation of in-situ stresses has significant applications in earth sciences and subsurface engineering, such as fault zone studies, underground CO₂ sequestration, nuclear waste repositories, oil and gas reservoir development, and geothermal energy exploitation. Over the past few decades, Diagnostic Fracture Injection Tests (DFIT), which have also been referred to as Injection-Falloff Tests, Fracture Calibration Tests, and Mini-Frac Tests, have evolved into a commonly used and reliable technique to obtain in-situ stress. Simplifying assumptions used in traditional methods often lead to inaccurate estimation of the in-situ stress, even for a planar fracture geometry. When a DFIT is conducted in naturally fractured reservoirs, the stimulated natural fractures can either alter the effective reservoir permeability within the distance of investigation or interact with the hydraulic fracture to form a complex fracture geometry, this further complicates stress estimation. In this study, we present a new pressure transient model for DFIT analysis in naturally fractured reservoirs. By analyzing synthetic, laboratory and field cases, we found that fracture complexity and permeability evolution can be detected from DFIT data. Most importantly, it is shown that using established methods to pick minimum in-situ stress often lead to over or underestimates, regardless of whether the reservoir is heavily fractured or sparsely fractured. Our proposed “variable compliance method” gives a much more accurate and reliable estimation of in-situ stress in both homogenous and naturally fractured reservoirs. By combining the unique pressure signatures associated with the closure of natural fractures, a lower bound on the horizontal stress anisotropy can be estimated.

Appendix: Modeling Pressure Transient Behavior during DFIT using Method of Lines (MOL)

In essence, DFIT analysis is a pressure transient analysis. However, unlike pressure transient analysis of tradition well-testing techniques, the fracture cannot be treated as a static and the leak-off rate does not follow Carter’s leak-off assumption (i.e., constant fracturing pressure), but rather coupled with variable fracture-wellbore system compliance/stiffness during fracture closure. Classic well-test solutions normally assume a constant injection rate, but in reality, “constant injection rate” does not equal “constant leak-off rate into formation”, because over 90% of injected fluid stay inside fracture at the end of pumping, instead of leaking into formation, thus, make DFIT violate the required boundary condition for using existing well-test solutions. That’s why G-function and classic well-test solution based models can lead to incorrect interpretation and are not capable of bridging both before and after closure data coherently. Figure 24 illustrates a linear leak-off from fracture surface into the formation.

Fig. 24

Illustration of one-dimensional leak-off

As discussed in Sect. 2.1, the pressure transient behavior during DFIT is uniquely described by the following equations:

$$\frac{{\partial P}}{{\partial t}}=\frac{1}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{\partial }{{\partial x}}\left( {k\frac{{\partial P}}{{\partial x}}} \right)$$

(19)

$$\frac{k}{{{\mu _{\text{f}}}}}~\frac{{{\text{d}}P}}{{{\text{d}}x}}=\frac{1}{{2{S_{\text{f}}}}}\frac{{{\text{d}}{P_{\text{f}}}}}{{{\text{d}}t}}~\quad {\text{at}}~x=0$$

(20)

$$P={P_0}~\quad {\text{at}}\;t=0,~\quad x>0$$

(21)

$$~~P={\text{ISIP~}}\quad {\text{at}}\;t=0,~\quad x=0$$

(22)

Since the permeability k in the partial differential equation (PDE) of Eq. (19) is not limited to a constant value and the boundary condition at the fracture surface (i.e., x = 0) is an ordinary differential equation (ODE) by itself, the analytical solution does not exist. To solve this system of PDE with ODE boundary condition, the concept of method of lines (MOL) is used, to replace the spatial derivative in the PDE with algebraic approximations, and then the PDE system can be transformed into a system of ODEs, which can be solved simultaneously and efficiently by well-established numerical methods. Since the MOL essentially replaces the problem PDEs with systems of approximating ODEs, the addition of other ODEs is easily accomplished.

Let divide the reservoir domain in the x-direction into a number of M points with uniform spacing of $\varDelta x$. Using the finite difference method, Eq. (19) can be represented in a discretized manner as:

$$\frac{{{\text{d}}{P_{\text{i}}}}}{{{\text{dt}}}}=\frac{1}{{{{{{\upmu}}}_{\text{f}}}\phi {{\text{c}}_{\text{t}}}}}\frac{{\left( {{k_{\text{i}}}+{k_{{\text{i}}+1}}} \right)\left( {{P_{{\text{i}}+1}} - {P_{\text{i}}}} \right) - \left( {{k_{\text{i}}}+{k_{{\text{i}} - 1}}} \right)\left( {{P_{\text{i}}} - {P_{{\text{i}} - 1}}} \right)}}{{2\Delta {x^2}}},{\text{~}}2 \leq {\text{i}} \leq {\text{M}} - 1$$

(23)

where i is an index designating a position along a grid in the x-direction. The initial condition can be written as:

$$~{P_i}=\left\{ {\begin{array}{*{20}{c}} {{\text{ISIP}},~~~~~~~~~i=1} \\ {{P_0},~~~~~~~~~~~~~i \geq 2} \end{array}} \right.~\quad {\text{at}}~t=0$$

(24)

At the boundary of the fracture surface, we can have

$$\frac{{{\text{d}}{P_1}}}{{{\text{d}}t}}=\frac{{2{S_{\text{f}}}{k_1}}}{{{\mu _{\text{f}}}}}~\frac{{{P_2} - {P_1}}}{{\Delta x}}$$

(25)

If the simulation domain is large enough compared to the simulated time scale, then pressure transient front will not reach the boundary and it can be treated as infinite acting boundary condition where$P={P_{0~}}\;{\text{as}}\;x \to \infty$. Just for the purpose of completing the ODE system, here we assume no flux boundary condition (it is also a symmetric condition where at a fictitious point M + 1 outside the grid in x satisfying$~{P_{M+1}}={P_{M - 1}}$) at the M point:

$$\frac{{{\text{d}}{P_M}}}{{{\text{d}}t}}=\frac{{{k_M}}}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{{P_{M - 1}} - 2{P_M}+{P_{M - 1}}}}{{\Delta {x^2}}}$$

(26)

Combine Eqs. (22), (24) and (25), a system ODE for initial value problem can be assembled:

$$\left[ {\begin{array}{*{20}{c}} {\frac{{{\text{d}}{P_1}}}{{{\text{d}}t}}} \\ {\frac{{{\text{d}}{P_2}}}{{{\text{d}}t}}} \\ {\begin{array}{*{20}{c}} \vdots \\ {\frac{{{\text{d}}{P_{M - 1}}}}{{{\text{d}}t}}} \\ {\frac{{{\text{d}}{P_M}}}{{{\text{d}}t}}} \end{array}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\frac{{2{S_{\text{f}}}{k_1}}}{{{\mu _{\text{f}}}}}~\frac{{{P_2} - {P_1}}}{{\Delta x}}} \\ {\frac{1}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{\left( {{k_2}+{k_3}} \right)\left( {{P_3} - {P_2}} \right) - \left( {{k_2}+{k_1}} \right)\left( {{P_2} - {P_1}} \right)}}{{2\Delta {x^2}}}} \\ {\begin{array}{*{20}{c}} \vdots \\ {\frac{1}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{\left( {{k_{M - 1}}+{k_M}} \right)\left( {{P_M} - {P_{M - 1}}} \right) - \left( {{k_{M - 1}}+{k_{M - 2}}} \right)\left( {{P_{M - 1}} - {P_{M - 2}}} \right)}}{{2\Delta {x^2}}}} \\ {\frac{{{k_M}}}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{{P_{M - 1}} - 2{P_M}+{P_{M - 1}}}}{{\Delta {x^2}}}} \end{array}} \end{array}} \right]$$

(27)

The first order time derivative can be approximated using a backward finite difference:

$$\frac{{\partial {P_i}}}{{\partial t}}~ \approx \frac{{P_{i}^{n} - P_{i}^{{n - 1}}}}{{\Delta t}}+O(\Delta t)$$

(28)

where t moves forward in steps that indexed by n. Substitute Eq. (25) into Eq. (26) we can get

$$\left[ {\begin{array}{*{20}{c}} {\frac{{P_{1}^{n} - P_{1}^{{n - 1}}}}{{\Delta t}}} \\ {\frac{{P_{2}^{n} - P_{2}^{{n - 1}}}}{{\Delta t}}} \\ {\begin{array}{*{20}{c}} \vdots \\ {\frac{{P_{{M - 1}}^{n} - P_{{M - 1}}^{{n - 1}}}}{{\Delta t}}} \\ {\frac{{P_{M}^{n} - P_{M}^{{n - 1}}}}{{\Delta t}}} \end{array}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\frac{{2{S_{\text{f}}}{k_1}}}{{{\mu _{\text{f}}}}}~\frac{{P_{2}^{n} - P_{1}^{n}}}{{\Delta x}}} \\ {\frac{1}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{\left( {k_{2}^{n}+k_{3}^{n}} \right)\left( {P_{3}^{n} - P_{2}^{n}} \right) - \left( {k_{2}^{n}+k_{1}^{n}} \right)\left( {P_{2}^{n} - P_{1}^{n}} \right)}}{{2\Delta {x^2}}}} \\ {\begin{array}{*{20}{c}} \vdots \\ {\frac{1}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{\left( {k_{{M - 1}}^{n}+k_{M}^{n}} \right)\left( {P_{M}^{n} - P_{{M - 1}}^{n}} \right) - \left( {k_{{M - 1}}^{n}+k_{{M - 2}}^{n}} \right)\left( {P_{{M - 1}}^{n} - P_{{M - 2}}^{n}} \right)}}{{2\Delta {x^2}}}} \\ {\frac{{{k_M}}}{{{\mu _{\text{f}}}\phi {c_{\text{t}}}}}\frac{{P_{{M - 1}}^{n} - 2P_{M}^{n}+P_{{M - 1}}^{n}}}{{\Delta {x^2}}}} \end{array}} \end{array}} \right]$$

(29)

Now we can solve Eq. (29) explicitly for the solution at an advanced time step $P_{i}^{n}$ in terms of the solution of the previous time step $P_{i}^{{n - 1}}$. However, since $P_{{i - 1}}^{n}$ is unknown so Eq. (29) is implicit in $P_{i}^{n}$. For each grid point, the full set of algebraic equations has to be solved simultaneously.