Skip to main content
SpringerLink
Log in

A grain boundary damage model for delamination

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

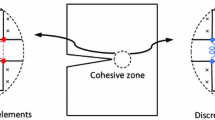
Abstract

Intergranular failure in metallic materials represents a multiscale damage mechanism: some feature of the material microstructure triggers the separation of grain boundaries on the microscale, but the intergranular fractures develop into long cracks on the macroscale. This work develops a multiscale model of grain boundary damage for modeling intergranular delamination—a failure of one particular family of grain boundaries sharing a common normal direction. The key feature of the model is a physically-consistent and mesh independent, multiscale scheme that homogenizes damage at many grain boundaries on the microscale into a single damage parameter on the macroscale to characterize material failure across a plane. The specific application of the damage framework developed here considers delamination failure in modern Al–Li alloys. However, the framework may be readily applied to other metals or composites and to other non-delamination interface geometries—for example, multiple populations of material interfaces with different geometric characteristics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Anderson TL (2005) Engineering fracture mechanics. Taylor & Francis Group, London

    Google Scholar 

  2. Babel HW, Farahmand B, Yousefiani A (2003) Assessment of delaminations in current aluminum–lithium alloys. Technical report, Boeing

  3. Banerji SK, McMahon CJ Jr, Feng HC (1987) Intergranular fracture in 4340-type steels: effects of impurities and hydrogen. Metall Trans

  4. Barlat F, Aretz H, Yoon JW, Karabin ME, Brem JC, Dick RE (2005) Linear transformation-based anisotropic yield functions. Int J Plast 21:1009–1039

    Article  MATH  Google Scholar 

  5. Baz̆ant ZP, Lin F (1988) Nonlocal smeared cracking model for concrete fracture. J Struct Eng 114(11):2493–2510

    Article  Google Scholar 

  6. Beaudoin AJ, Obstalecki M, Tayon W, Hernquist M, Mudrock R, Kenesei P, Lienert U (2013) In situ assessment of lattice strain in an Al–Li alloy. Acta Mater 61:3456–3464

    Article  Google Scholar 

  7. Chen PS, Stanton WP (1996) A new aging treatment for improving cryogenic toughness of the main structural alloy of the super lightweight tank. Technical Report 108524, NASA

  8. Chen PS, Stanton WP (2002) Cryogenic fracture toughness imprimprove for the super-lightweight tank’s main structural alloy. Technical Report 2002–21547, NASA

  9. Cocks ACF, Ashby MF (1980) Intergranular fracture during power-law creep under multiaxial stresses. Metal Sci 14:395–402

    Article  Google Scholar 

  10. Confalonieri F, Ghisi A, Cocchetti G, Corigliano A (2014) A domain decomposition approach for the simulation of fracture phenomena in polycrystalline microsystems. Comput Methods Appl Mech Eng 277:180–218

    Article  MathSciNet  Google Scholar 

  11. Crooks R, Domack MS, Wagner JA (2006) Microtexture and nanoindentation study of delamination cracking in Al–Cu–Li–X alloys. WIT Trans Built Environ 85:549–557

    Google Scholar 

  12. De PS, Mishra RS, Baumann JA (2011) Characterization of high cycle fatigue behavior of a new generation aluminum lithium alloy. Acta Mater 59:5946–5960

    Article  Google Scholar 

  13. d’Escata Y, Devaux JC (1979) Numerical study of the initiation, stable crack growth, and maximum load with a ducticle fracture criterion based on the growth of holes. In: ASTM STP 668. American Society of Testing and Materials, pp 229–248

  14. Edward GH, Ashby MF (1979) Intergranular fracture druing power-law creep. Acta Metall 27:1505–1518

    Article  Google Scholar 

  15. Espinosa HD, Zavattieri PD (2003) A grain level model for the study of failure initiation and evolution in polycrystalline brittle materials. Part I: theory and numerical implementation. Mech Mater 35:333–364

    Article  Google Scholar 

  16. Espinosa HD, Zavattieri PD (2003) A grain level model for the study of failure initiation and evolution in polycrystalline brittle materials. Part II: numerical examples. Mech Mater 35:365– 394

    Article  Google Scholar 

  17. Evers LP, Parks DM, Brekelmans WAM, Geers MGD (2002) Crystal plasticity model with enhanced hardening by geometrically necessary dislocation accumulation. J Mech Phys Solids 50:2403–2424

    Article  MATH  Google Scholar 

  18. Farkas D, van Swygenhoven H, Derlet PM (2002) Intergranular fracture in nanocrystalline metals. Phys Rev B 66:060101

    Article  Google Scholar 

  19. Fish J, Belsky V (1995) Multigrid method for periodic heterogeneous media Part 1: convergence studies for one-dimensional case. Comput Methods Appl Mech Eng 126:1–16

    Article  MATH  MathSciNet  Google Scholar 

  20. Fish J, Belsky V (1995) Multi-grid method for periodic heterogeneous media Part 2: multiscale modeling and quality control in multidimensional case. Comput Methods Appl Mech Eng 126:17–38

    Article  MATH  MathSciNet  Google Scholar 

  21. Fish J, Shek K (2000) Multiscale analysis of composite materials and structures. Compos Sci Technol 60:2547–2556

    Article  Google Scholar 

  22. Fish J, Shek K, Pandheeradi M, Shepard MS (1997) Computational plasticity for composite structures based on mathematical homogenization: theory and practice. Comput Methods Appl Mech Eng 148:53–73

    Article  MATH  Google Scholar 

  23. Ghosh S, Moorthy S (1995) Elastic-plastic analysis of arbitary heterogeneous materials with the Voronoi cell finite element method. Comput Methods Appl Mech Eng 121:373–409

    Article  MATH  Google Scholar 

  24. Ghosh S, Lee K, Moorthy S (1995) Multiple scale analysis of heterogeneous elastic structures using homogenization theory and Voronoi cell finite element method. Int J Solids Struct 32(1):27–62

    Article  MATH  MathSciNet  Google Scholar 

  25. Ghosh S, Lee K, Moorthy S (1996) Two scale analysis of heterogeneous elastic-plastic materials with asymptotic homogenization and Voronoi cell finite element model. Comput Methods Appl Mech Eng 132:63–116

    Article  MATH  Google Scholar 

  26. Ghosh S, Ling Y, Majumdar B, Kim R (2000) Interfacial debonding analysis in multiple fiber reinforced composites. Mech Mater 32:561–591

    Article  Google Scholar 

  27. Ghosh S, Lee K, Raghavan P (2001) A multi-level computational model for multi-scale damage analysis in composite and porous materials. Int J Solids Struct 38:2335–2385

    Article  MATH  Google Scholar 

  28. Girard L, Bouillon S, Weiss J, Amitrano D, Fichefet T, Legat V (2011) A new modeling framework for sea-ice mechanics based on elasto-brittle rheology. Ann Glaciol 52(57):123–132

    Article  Google Scholar 

  29. Green AE, Naghdi PM (1965) A general theory of an elastic-plastic continuum. Arch Ration Mech Anal 18:251–281

    Article  MATH  MathSciNet  Google Scholar 

  30. Guo W, Dong H, Lu M, Zhao X (2002) The coupled effects of thickness and delamination on cracking resistance of X70 pipline steel. Int J Press Vessels Pip 79:403–412

    Article  Google Scholar 

  31. Gurson AL (1977) Continuum theory of ductile rupture by void nucleation and growth: part I - yield criteria and flow rules for porous ductile media. J Eng Mater Technol 99(1):2–15

    Article  Google Scholar 

  32. Hernquist MW (2010) Effects of crack arresting delaminations in aluminum–lithium alloys. Master’s thesis, University of Illinois at Urbana-Champaign

  33. Johnston WM, Pollock WD, Dawicke DS (2002) Biaxial testing of 2195 aluminum lithium alloy using cruciform specimens. Technical Report CR-2002-211942, NASA

  34. Kachanov LM (1999) On rupture time under creep conditions. Int J Fract 97:xi–xviii

  35. Kanoute P, Boso DP, Chaboche JL, Schrefler BA (2009) Multiscale methods for composites: a review. Arch Comput Methods Eng 16:31–75

    Article  MATH  Google Scholar 

  36. Knutsen RD, Hutchings R (1988) Occurence of non-metallic inclusions in 3CR12 steel and their effect on impact toughness. Mater Sci Technol A 4:127–135

    Article  Google Scholar 

  37. Kok S, Beaudoin AJ, Tortorelli DA (2002) A polycrystal plasticity model based on the mechanical threshold. Int J Plast 18:715–741

    Article  MATH  Google Scholar 

  38. Kraft RH, Molinari JF (2008) A statistical investigation of effects of grain boundary properties on transgranular fracture. Acta Mater 56:4739–4749

    Article  Google Scholar 

  39. Lee K, Moorthy S, Ghosh S (1999) Multiple scale computational model for damage in composite materials. Comput Methods Appl Mech Eng 172:175–201

    Article  MATH  Google Scholar 

  40. McMahon CJ Jr (2001) Hydrogen-induced intergranular fracture of steels. Eng Fract Mech 68:731–788

    Article  Google Scholar 

  41. Messner MC, Beaudoin AJ, Dodds RH (2014) Mesoscopic modeling of crack arrrestor delamination in Al–Li: primary crack shielding and T-stress effect. Int J Fract 188:229–249

    Article  Google Scholar 

  42. Messner MC, Beaudoin AJ, Dodds RH (2015) An interface compatibility/equilibrium mechanism for delamination fracture in aluminum–lithium alloys. Eng Fract Mech 133:70–84

    Article  Google Scholar 

  43. Messner MC, Beaudoin AJ, Dodds RH, Consistent crystal plasticity kinematics and linearization for the implicit finite element method. Eng Comput (In press)

  44. Mura T (1991) Micromechanics of defects in solids. Martinus Nijhoff, Boston

    Google Scholar 

  45. Ovid’ko IA (2007) Review on the fracture processes in nanocrystalline materials. J Mater Sci 42:1694–1708

    Article  Google Scholar 

  46. Raj R (1978) Intergranular fracture in bicrystals. Acta Metall 26:341–349

    Article  Google Scholar 

  47. Raj R, Ashby MF (1975) Intergranular fracture at elevated temperature. Acta Metall 23:653–666

    Article  Google Scholar 

  48. Rashid YR (1968) Ultimate strength analysis of prestressed concrete pressure vessels. Nucl Eng Des 7:334–344

    Article  Google Scholar 

  49. Reuss A (1929) Berechnung der fiessgrenze von mischkristallen auf grund der plastizitaetsbeding fuer einkristalle. Zeitschrift fuer Angewandte Mathematik und Mechanik 9:49–58

    Article  MATH  Google Scholar 

  50. Rice JR, Tracey DM (1969) On the ductile enlargement of voids in triaxial stress fields. J Mech Phys Solids 17:201–217

    Article  Google Scholar 

  51. Rioja RJ, Liu J (2012) The evolution of Al–Li base products for aerospace and space applications. Metall Mater Trans A 43:3325–3337

    Article  Google Scholar 

  52. Schubbe JJ (2009) Fatigue crack propagation in 7050–T7451 plate alloy. Eng Fract Mech 76:1037–1048

    Article  Google Scholar 

  53. Scott P (1994) A review of irradiation assisted stress corrosion cracking. J Nucl Mater 211:101–112

    Article  Google Scholar 

  54. Tanaka K, Mori T (1972) Note on volume integrals of the elastic field around an ellipsoidal inclusion. J Elast 2:199–200

    Article  Google Scholar 

  55. Tayon W, Crooks R, Domack M, Wagner J (2010) EBSD study of delamination fracture in Al–Li Alloy 2090. Exp Mech 50:135–143

    Article  Google Scholar 

  56. Tvergaard V, Needleman A (1984) Analysis of the cup-cone fracture in a round tensile bar. Acta Metall 32(1):157–169

    Article  Google Scholar 

  57. Vander Kooi DC, Park W, Hilton MR (1999) Characterization of cryogenic mechanical properties of aluminum–lithium alloy C-458. Scripta Mater 41:1185–1190

    Article  Google Scholar 

  58. Venkateswara Rao KT, Ritchie RO (1989) Mechanical properties of Al–Li alloys Part 1 fracture toughness and microstructure. Mater Sci Technol 5:882–895

    Article  Google Scholar 

  59. Venkateswara Rao KT, Ritchie RO (1992) Fatigue of aluminum–lithium alloys. Int Mater Rev 37(4):153–185

    Google Scholar 

  60. Venkateswara Rao KT, Yu W, Ritchie RO (1988) Fatigue crack propogation in aluminum–lithium alloy 2090: part I. Long crack behavior. Metall Mater Trans A 19A:549–561

    Article  Google Scholar 

  61. Venkateswara Rao KT, Yu W, Ritchie RO (1988) Fatigue crack propogation in aluminum–lithium alloy 2090: part II. Small crack behavior. Metall Mater Trans A 19A:563–569

    Google Scholar 

  62. Venkateswara Rao KT, Yu W, Ritchie RO (1988) On the behavior of small fatigue cracks in commercial aluminum–lithium alloys. Eng Fract Mech 31:623–635

    Article  Google Scholar 

  63. Venkateswara Rao KT, Yu W, Ritchie RO (1989) Cryogenic toughness of commercial aluminum–lithium alloys: role of delamination toughening. Metall Trans A 20A:485–497

    Article  Google Scholar 

  64. Venkateswara Rao KT, Bucci RJ, Jata KV, Ritchie RO (1991) A comparison of fatigue-crack propogation behavior in sheet and plate aluminum–lithium alloys. Mater Sci Eng A141:39–48

    Article  Google Scholar 

  65. Voigt W (1889) Ueber die beziehung zwischen den beiden elastizitaetskonstanten isotroper koerper. Annalen der Physik (Wiedemann) 38:573–587

    Article  Google Scholar 

  66. White CL, Padgett RA, Liu CT, Yalisove SM (1984) Sucracking grain boundary segregation in relation to intergranular fracture: boron and sulfur in \(Ni_{3}Al\). Scripta Mater 18:1714–1720

    Google Scholar 

  67. Yu W, Ritchie RO (1987) Fatigue crack propogation in 2090 aluminum–lithium alloy: effect of compression overload cycles. J Eng Mater Technol 109:81–85

    Article  Google Scholar 

Download references

Acknowledgments

M. C. Messner’s contribution was in part supported by the Department of Defense (DoD) through the National Defense Science & Engineering Graduate Fellowship (NDSEG) Program and in part performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344 (LLNL-JRNL-666218). A. J. Beaudoin recieved support through the U.S. Department of Energy under Contract DEFG36-05GO15049. R. H. Dodds received support from the M. T. Geoffrey Yeh Chair Fund.

Author information

Author notes

  1. M. C. Messner

    Present address: Lawrence Livermore National Laboratory, P.O. Box 808, L-227, Livermore, CA, 94551, USA

Authors and Affiliations

  1. Department of Civil and Environmental Engineering, 2113 NCEL, University of Illinois at Urbana-Champaign, MC 250, 205 N. Mathews Avenue, Urbana, IL, 61801, USA

    M. C. Messner & R. H. Dodds Jr.

  2. Department of Mechanical Science and Engineering, 354 MEB, University of Illinois at Urbana-Champaign, MC 244, 1204 Green Street, Urbana, IL, 61801, USA

    A. J. Beaudoin

Authors
  1. M. C. Messner
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. J. Beaudoin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. R. H. Dodds Jr.
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. H. Dodds Jr..

Projection matrices

Projection matrices

This appendix lists the components of the three projection tensors describe above—\(\mathbf {P}_{3\times 6}^{e}\), \(\mathbf {P}_{3\times 6}^{c}\), and \(\mathbf {P}_{6\times 6}^{D}\). Each matrix is a combination of the components of the orthogonal coordinate system describing the interface plane/grain boundaries with normal vector \(\mathbf {n}\) and transverse vectors \(\mathbf {s}\) and \(\mathbf {t}\). Let the components of these vectors be:

$$\begin{aligned} \mathbf {n}= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c} n_{1}&n_{2}&n_{3}\end{array}\right] ^{T}\\ \mathbf {s}= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c} s_{1}&s_{2}&s_{3}\end{array}\right] ^{T}\\ \mathbf {t}= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c} t_{1}&t_{2}&t_{3}\end{array}\right] ^{T} \end{aligned}$$

As described above, under large deformations and rotations these vectors remain constant in the corotational configuration. The form of the projection matrices depends on the Voigt notation used in the finite element framework. The particular Voigt notation in this work is:

$$\begin{aligned}&{\varvec{\varepsilon }}\rightarrow \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \varepsilon _{11}&\varepsilon _{22}&\varepsilon _{33}&2\varepsilon _{12}&2\varepsilon _{23}&2\varepsilon _{13}\end{array}\right] ^{T}\\&{\varvec{\sigma }}\rightarrow \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \sigma _{11}&\sigma _{22}&\sigma _{33}&\sigma _{12}&\sigma _{23}&\sigma _{13}\end{array}\right] ^{T}. \end{aligned}$$

The components of each projection are:

$$\begin{aligned}&\mathbf {P}_{3\times 6}^{e}=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} n_{1} &{}0 &{}0 &{}n_{2} &{}0 &{}n_{3}\\ 0 &{}n_{2} &{}0 &{}n_{1} &{}n_{3} &{}0\\ 0 &{}0 &{}n_{3} &{}0 &{}n_{2} &{}n_{1} \end{array}\right] \\&\mathbf {P}_{3\times 6}^{c}\\&\quad =\left[ \begin{array}{llllll} s_{1}^{2} &{}s_{2}^{2} &{}s_{3}^{2} &{}s_{1}s_{2} &{}s_{2}s_{3} &{}s_{1}s_{3}\\ t_{1}^{2} &{}t_{2}^{2} &{}t_{3}^{2} &{}t_{1}t_{2} &{}t_{2}t_{3} &{}t_{1}t_{3}\\ s_{1}t_{1} &{}s_{2}t_{2} &{}s_{3}t_{3} &{}\frac{1}{2}\left( s_{2}t_{1}+s_{1}t_{2}\right) &{}\frac{1}{2}\left( s_{2}t_{3}+s_{3}t_{2}\right) &{}\frac{1}{2}\left( s_{3}t_{1}+s_{1}t_{3}\right) \end{array}\right] \end{aligned}$$

and

$$\begin{aligned} \mathbf {P}_{6\times 6}^{D}=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} p_{11} &{}\quad p_{12} &{}\quad p_{13} &{}\quad p_{14} &{}\quad p_{15} &{}\quad p_{16}\\ p_{21} &{}\quad p_{22} &{}\quad p_{23} &{}\quad p_{24} &{}\quad p_{25} &{}\quad p_{26}\\ p_{31} &{}\quad p_{32} &{}\quad p_{33} &{}\quad p_{34} &{}\quad p_{35} &{}\quad p_{36}\\ p_{41} &{}\quad p_{42} &{}\quad p_{43} &{}\quad p_{44} &{}\quad p_{45} &{}\quad p_{46}\\ p_{51} &{}\quad p_{52} &{}\quad p_{53} &{}\quad p_{54} &{}\quad p_{55} &{}\quad p_{56}\\ p_{61} &{}\quad p_{62} &{}\quad p_{63} &{}\quad p_{64} &{}\quad p_{65} &{}\quad p_{66} \end{array}\right] \end{aligned}$$

with:

$$\begin{aligned} p_{11}&=n_{1}^{2}\left( n_{1}^{2}+2\left( s_{1}^{2}+t_{1}^{2}\right) \right) \\ p_{12}&=n_{1}n_{2}\left( n_{1}n_{2}+2s_{1}s_{2}+2t_{1}t_{2}\right) \\ p_{13}&=n_{1}n_{3}\left( n_{1}n_{3}+2s_{1}s_{3}+2t_{1}t_{3}\right) \\ p_{14}&=2n_{1}\left( n_{1}\left( s_{1}s_{2}+t_{1}t_{2}\right) +n_{2}\left( s_{1}^{2}+t_{1}^{2}\right) +n_{2}n_{1}^{2}\right) \\ p_{15}&=2n_{1}\left( n_{3}\left( s_{1}s_{2}+t_{1}t_{2}\right) +n_{2}\left( s_{1}s_{3}+t_{1}t_{3}\right) +n_{1}n_{2}n_{3}\right) \\ p_{16}&=2n_{1}\left( n_{1}\left( s_{1}s_{3}+t_{1}t_{3}\right) +n_{3}\left( s_{1}^{2}+t_{1}^{2}\right) +n_{3}n_{1}^{2}\right) \\ p_{21}&=n_{1}n_{2}\left( n_{1}n_{2}+2s_{1}s_{2}+2t_{1}t_{2}\right) \\ p_{22}&=n_{2}\left( 2n_{2}\left( s_{2}^{2}+t_{2}^{2}\right) +n_{2}^{3}\right) \\ p_{23}&=n_{2}n_{3}\left( n_{2}n_{3}+2s_{2}s_{3}+2t_{2}t_{3}\right) \\ p_{24}&=2n_{2}\left( n_{2}\left( s_{1}s_{2}+t_{1}t_{2}\right) +n_{1}\left( n_{2}^{2}+s_{2}^{2}+t_{2}^{2}\right) \right) \\ p_{25}&=2n_{2}\left( n_{2}\left( s_{2}s_{3}+t_{2}t_{3}\right) +n_{3}\left( s_{2}^{2}+t_{2}^{2}\right) +n_{3}n_{2}^{2}\right) \\ p_{26}&=2n_{2}\left( n_{3}\left( s_{1}s_{2}+t_{1}t_{2}\right) +n_{1}\left( n_{2}n_{3}+s_{2}s_{3}+t_{2}t_{3}\right) \right) \\ p_{31}&=n_{1}n_{3}\left( n_{1}n_{3}+2s_{1}s_{3}+2t_{1}t_{3}\right) \\ p_{32}&=n_{2}n_{3}\left( n_{2}n_{3}+2s_{2}s_{3}+2t_{2}t_{3}\right) \\ p_{33}&=n_{3}^{2}\left( n_{3}^{2}+2\left( s_{3}^{2}+t_{3}^{2}\right) \right) \\ p_{34}&=2n_{3}\left( n_{2}\left( s_{1}s_{3}+t_{1}t_{3}\right) +n_{1}\left( n_{2}n_{3}+s_{2}s_{3}+t_{2}t_{3}\right) \right) \\ \end{aligned}$$
$$\begin{aligned} p_{35}&=n_{3}\left( 2n_{3}\left( s_{2}s_{3}+t_{2}t_{3}\right) +2n_{2}\left( n_{3}^{2}+s_{3}^{2}+t_{3}^{2}\right) \right) \\ p_{36}&=n_{3}\left( 2n_{3}\left( s_{1}s_{3}+t_{1}t_{3}\right) +2n_{1}\left( n_{3}^{2}+s_{3}^{2}+t_{3}^{2}\right) \right) \\ p_{41}&=n_{1}\left( n_{1}\left( s_{1}s_{2}+t_{1}t_{2}\right) +n_{2}\left( s_{1}^{2}+t_{1}^{2}\right) +n_{2}n_{1}^{2}\right) \\ p_{42}&=n_{2}\left( n_{2}\left( s_{1}s_{2}+t_{1}t_{2}\right) +n_{1}\left( n_{2}^{2}+s_{2}^{2}+t_{2}^{2}\right) \right) \\ p_{43}&=n_{3}\left( n_{2}\left( s_{1}s_{3}+t_{1}t_{3}\right) +n_{1}\left( n_{2}n_{3}+s_{2}s_{3}+t_{2}t_{3}\right) \right) \\ p_{44}&=n_{1}^{2}\left( 2n_{2}^{2}+s_{2}^{2}+t_{2}^{2}\right) +2n_{2}n_{1}\left( s_{1}s_{2}+t_{1}t_{2}\right) \\&\quad +n_{2}^{2}\left( s_{1}^{2}+t_{1}^{2}\right) \\ p_{45}&=n_{2}\left( n_{3}\left( s_{1}s_{2}+t_{1}t_{2}\right) +n_{2}\left( s_{1}s_{3}+t_{1}t_{3}\right) \right) \\&\quad + n_{1}\left( n_{2}\left( s_{2}s_{3}+t_{2}t_{3}\right) +n_{3}\left( s_{2}^{2}+t_{2}^{2}\right) +2n_{3}n_{2}^{2}\right) \\ p_{46}&=n_{1}^{2} \left( 2n_{2}n_{3}+s_{2}s_{3}+t_{2}t_{3}\right) \\&\quad + n_{1}\left( n_{3}\left( s_{1}s_{2}+t_{1}t_{2}\right) + n_{2}\left( s_{1}s_{3}+t_{1}t_{3}\right) \right) \\&\quad + n_{2}n_{3}\left( s_{1}^{2}+t_{1}^{2}\right) \\ p_{51}&=n_{1}\left( n_{3}\left( s_{1}s_{2}+t_{1}t_{2}\right) +n_{2}\left( s_{1}s_{3}+t_{1}t_{3}\right) +n_{1}n_{2}n_{3}\right) \\ p_{52}&=n_{2}\left( n_{2}\left( s_{2}s_{3}+t_{2}t_{3}\right) +n_{3}\left( s_{2}^{2}+t_{2}^{2}\right) +n_{3}n_{2}^{2}\right) \\ p_{53}&=n_{3}\left( n_{3}\left( s_{2}s_{3}+t_{2}t_{3}\right) +n_{2}\left( n_{3}^{2}+s_{3}^{2}+t_{3}^{2}\right) \right) \\ \end{aligned}$$
$$\begin{aligned} p_{54}&=n_{2}\left( n_{3}\left( s_{1}s_{2}+t_{1}t_{2}\right) +n_{2}\left( s_{1}s_{3}+t_{1}t_{3}\right) \right) \\&\quad + n_{1}\left( n_{2}\left( s_{2}s_{3}+t_{2}t_{3}\right) +n_{3}\left( s_{2}^{2}+t_{2}^{2}\right) +2n_{3}n_{2}^{2}\right) \\ p_{55}&=n_{2}^{2}\left( 2n_{3}^{2}+s_{3}^{2}+t_{3}^{2}\right) +2n_{3}n_{2}\left( s_{2}s_{3}+t_{2}t_{3}\right) \\&\quad +n_{3}^{2}\left( s_{2}^{2}+t_{2}^{2}\right) \\ p_{56}&=n_{3}\left( n_{3}\left( s_{1}s_{2}+t_{1}t_{2}\right) +n_{2}\left( s_{1}s_{3}+t_{1}t_{3}\right) \right) \\&\quad + n_{1}\left( n_{3}\left( s_{2}s_{3}+t_{2}t_{3}\right) +n_{2}\left( 2n_{3}^{2}+s_{3}^{2}+t_{3}^{2}\right) \right) \\ p_{61}&=n_{1}\left( n_{1}\left( s_{1}s_{3}+t_{1}t_{3}\right) +n_{3}\left( s_{1}^{2}+t_{1}^{2}\right) +n_{3}n_{1}^{2}\right) \\ p_{62}&=n_{2}\left( n_{3}\left( s_{1}s_{2}+t_{1}t_{2}\right) +n_{1}\left( n_{2}n_{3}+s_{2}s_{3}+t_{2}t_{3}\right) \right) \\ p_{63}&=n_{3}\left( n_{3}\left( s_{1}s_{3}+t_{1}t_{3}\right) +n_{1}\left( n_{3}^{2}+s_{3}^{2}+t_{3}^{2}\right) \right) \\ p_{64}&=n_{1}^{2}\left( 2n_{2}n_{3}+s_{2}s_{3}+t_{2}t_{3}\right) \\&\quad + n_{1}\left( n_{3}\left( s_{1}s_{2}+t_{1}t_{2}\right) +n_{2}\left( s_{1}s_{3}+t_{1}t_{3}\right) \right) \\&\quad +n_{2}n_{3}\left( s_{1}^{2}+t_{1}^{2}\right) \\ p_{65}&=n_{3}\left( n_{3}\left( s_{1}s_{2}+t_{1}t_{2}\right) +n_{2}\left( s_{1}s_{3}+t_{1}t_{3}\right) \right) \\&\quad +n_{1}\left( n_{3}\left( s_{2}s_{3}+t_{2}t_{3}\right) +n_{2}\left( 2n_{3}^{2}+s_{3}^{2}+t_{3}^{2}\right) \right) \\ p_{66}&=n_{1}^{2}\left( 2n_{3}^{2}+s_{3}^{2}+t_{3}^{2}\right) +2n_{3}n_{1}\left( s_{1}s_{3}+t_{1}t_{3}\right) \\&\quad +n_{3}^{2}\left( s_{1}^{2}+t_{1}^{2}\right) . \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Messner, M.C., Beaudoin, A.J. & Dodds, R.H. A grain boundary damage model for delamination. Comput Mech 56, 153–172 (2015). https://doi.org/10.1007/s00466-015-1164-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-015-1164-z

Keywords

Search

Navigation