Skip to main content

Advertisement

SpringerLink
Log in

A hybrid smoothed extended finite element/level set method for modeling equilibrium shapes of nano-inhomogeneities

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

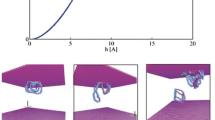
Interfacial energy plays an important role in equilibrium morphologies of nanosized microstructures of solid materials due to the high interface-to-volume ratio, and can no longer be neglected as it does in conventional mechanics analysis. When designing nanodevices and to understand the behavior of materials at the nano-scale, this interfacial energy must therefore be taken into account. The present work develops an effective numerical approach by means of a hybrid smoothed extended finite element/level set method to model nanoscale inhomogeneities with interfacial energy effect, in which the finite element mesh can be completely independent of the interface geometry. The Gurtin–Murdoch surface elasticity model is used to account for the interface stress effect and the Wachspress interpolants are used for the first time to construct the shape functions in the smoothed extended finite element method. Selected numerical results are presented to study the accuracy and efficiency of the proposed method as well as the equilibrium shapes of misfit particles in elastic solids. The presented results compare very well with those obtained from theoretical solutions and experimental observations, and the computational efficiency of the method is shown to be superior to that of its most advanced competitor.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Gurtin ME, Murdoch AI (1975) Continuum theory of elastic-material surfaces. Arch Ration Mech Anal 57:291–323. doi:10.1007/BF00261375

    Article  MathSciNet  MATH  Google Scholar 

  2. Gurtin ME, Weissmuller J, Larche F (1998) A general theory of curved deformable interfaces in solids at equilibrium. Philos Mag A 78:1093–1109. doi:10.1080/01418619808239977

    Google Scholar 

  3. Duan HL, Wang J, Huang ZP, Karihaloo BL (2005) Size-dependent effective elastic constants of solids containing nano-inhomogeneities with interface stress. J Mech Phys Solids 53:1574–1596. doi:10.1016/j.jmps.2005.02.009

    Article  MathSciNet  MATH  Google Scholar 

  4. Miller RE, Shenoy VB (2000) Size-dependent elastic properties of nanosized structural elements. Nanotechnology 11:139–147. doi:10.1088/0957-4484/11/3/301

    Article  Google Scholar 

  5. Sharma P, Ganti S (2004) Size-dependent Eshelby’s tensor for embedded nano-inclusions incorporating surface/interface energies. J Appl Mech-T ASME 71:663–671. doi:10.1115/1.1781177

    Article  MATH  Google Scholar 

  6. Zhao XJ, Qu J (2012) Effects of interfacial excess energy on the elastic field of a nano-inhomogeneity. Mech Mater 55:41–48. doi:10.1016/j.mechmat.2012.07.008

    Article  Google Scholar 

  7. Dingreville R, Qu JM, Cherkaoui M (2005) Surface free energy and its effect on the elastic behavior of nano-sized particles, wires and films. J Mech Phys Solids 53:1827–1854. doi:10.1016/j.jmps.2005.02.012

    Article  MathSciNet  MATH  Google Scholar 

  8. Zhao XJ, Rajapakse RKND (2009) Analytical solutions for a surface-loaded isotropic elastic layer with surface energy effects. Int J Eng Sci 47:1433–1444. doi:10.1016/j.ijengsci.2008.12.013

    Article  MathSciNet  MATH  Google Scholar 

  9. Olsson PAT, Park HS (2012) On the importance of surface elastic contributions to the flexural rigidity of nanowires. J Mech Phys Solids 60:2064–2083. doi:10.1016/j.jmps.2012.07.009

    Article  MathSciNet  Google Scholar 

  10. Gao W, Yu SW, Huang GY (2006) Finite element characterization of the size-dependent mechanical behaviour in nanosystems. Nanotechnology 17:1118–1122. doi:10.1088/0957-4484/17/4/045

    Article  Google Scholar 

  11. Tian L, Rajapakse RKND (2007) Finite element modelling of nanoscale inhomogeneities in an elastic matrix. Comp Mater Sci 41:44–53. doi:10.1016/j.commatsci.2007.02.013

    Article  Google Scholar 

  12. She H, Wang BA (2009) A geometrically nonlinear finite element model of nanomaterials with consideration of surface effects. Finite Elements Anal Des 45:463–467. doi:10.1016/j.finel.2009.01.002

    Article  MathSciNet  Google Scholar 

  13. Javili A, Steinmann P (2009) A finite element framework for continua with boundary energies. Part I: The two-dimensional case. Comput Method Appl Mech 198:2198–2208. doi:10.1016/j.cma.2009.02.008

    Article  MathSciNet  MATH  Google Scholar 

  14. Javili A, Steinmann P (2010) A finite element framework for continua with boundary energies. Part II: The three-dimensional case. Comput Method Appl Mech 199:755–765. doi:10.1016/j.cma.2009.11.003

    Article  MathSciNet  MATH  Google Scholar 

  15. He J, Lilley CM (2009) The finite element absolute nodal coordinate formulation incorporated with surface stress effect to model elastic bending nanowires in large deformation. Comput Mech 44:395–403. doi:10.1007/s00466-009-0380-9

    Article  MATH  Google Scholar 

  16. Yun G, Park HS (2008) A finite element formulation for nanoscale resonant mass sensing using the surface Cauchy–Born model. Comput Method Appl Mech 197:3324–3336. doi:10.1016/j.cma.2008.01.010

    Article  MathSciNet  MATH  Google Scholar 

  17. Park HS, Klein PA, Wagner GJ (2006) A surface Cauchy–Born model for nanoscale materials. Int J Numer Methods Eng 68:1072–1095. doi:10.1002/nme.1754

    Article  MathSciNet  MATH  Google Scholar 

  18. Park HS and Klein PA (2007) Surface Cauchy–Born analysis of surface stress effects on metallic nanowires. Phys Rev B 75: doi:10.1103/PhysRevB.75.085408

  19. Moes N, Dolbow J, Belytschko T (1999) A finite element method for crack growth without remeshing. Int J Numer Meth Eng 46:131–150. doi:10.1002/(SICI)1097-0207(19990910)46:1<131:AID-NME726>3.0.CO;2-J

    Google Scholar 

  20. Sukumar N, Chopp DL, Moes N, Belytschko T (2001) Modeling holes and inclusions by level sets in the extended finite-element method. Comput Method Appl Mech 190:6183–6200. doi:10.1016/S0045-7825(01)00215-8

    Article  MathSciNet  MATH  Google Scholar 

  21. Chessa J, Smolinski P, Belytschko T (2002) The extended finite element method (XFEM) for solidification problems. Int J Numer Meth Eng 53:1959–1977. doi:10.1002/Nme.386

    Article  MathSciNet  MATH  Google Scholar 

  22. Chessa J, Belytschko T (2003) An extended finite element method for two-phase fluids. J Appl Mech-T ASME 70:10–17. doi:10.1115/1.1526599

    Article  MathSciNet  MATH  Google Scholar 

  23. Duddu R, Bordas S, Chopp D, Moran B (2008) A combined extended finite element and level set method for biofilm growth. Int J Numer Methods Eng 74:848–870. doi:10.1002/Nme.2200

    Article  MathSciNet  MATH  Google Scholar 

  24. Duddu R, Chopp DL, Moran B (2009) A two-dimensional continuum model of biofilm growth incorporating fluid flow and shear stress based detachment. Biotechnol Bioeng 103:92–104. doi:10.1002/Bit.22233

    Article  Google Scholar 

  25. Fries TP, Belytschko T (2010) The extended/generalized finite element method: an overview of the method and its applications. Int J Numer Methods Eng 84:253–304. doi:10.1002/Nme.2914

    MathSciNet  MATH  Google Scholar 

  26. Bordas S, Nguyen PV, Dunant C, Guidoum A, Nguyen-Dang H (2007) An extended finite element library. Int J Numer Methods Eng 71:703–732. doi:10.1002/Nme.1966

    Article  MATH  Google Scholar 

  27. Yvonnet J, Le Quang H, He QC (2008) An XFEM/level set approach to modelling surface/interface effects and to computing the size-dependent effective properties of nanocomposites. Comput Mech 42:119–131. doi:10.1007/s00466-008-0241-y

    Article  MathSciNet  MATH  Google Scholar 

  28. Farsad M, Vernerey FJ, Park HS (2010) An extended finite element/level set method to study surface effects on the mechanical behavior and properties of nanomaterials. Int J Numer Methods Eng 84:1466–1489. doi:10.1002/Nme.2946

    Article  MathSciNet  MATH  Google Scholar 

  29. Liu GR, Dai KY, Nguyen TT (2007) A smoothed finite element method for mechanics problems. Comput Mech 39:859–877. doi:10.1007/s00466-006-0075-4

    Article  MATH  Google Scholar 

  30. Wachspress EL (1975) A rational finite element basis. Academic Press, New York

    MATH  Google Scholar 

  31. Shuttleworth R (1950) The surface tension of solids. Proc Phys Soc Lond A 63:444–457. doi:10.1088/0370-1298/63/5/302

    Article  Google Scholar 

  32. Osher S, Sethian JA (1988) Fronts propagating with curvature-dependent speed: algorithms based on Hamilton–Jacobi formulations. J Comput Phys 79:12–49. doi:10.1016/0021-9991(88)90002-2

    Article  MathSciNet  MATH  Google Scholar 

  33. Sukumar N, Prevost JH (2003) Modeling quasi-static crack growth with the extended finite element method Part I: computer implementation. Int J Solids Struct 40:7513–7537. doi:10.1016/j.ijsolstr.2003.08.002

    Article  MATH  Google Scholar 

  34. Moumnassi M, Belouettar S, Bechet E, Bordas SPA, Quoirin D, Potier-Ferry M (2011) Finite element analysis on implicitly defined domains: an accurate representation based on arbitrary parametric surfaces. Comput Method Appl Mech 200:774–796. doi:10.1016/j.cma.2010.10.002

    Article  MathSciNet  MATH  Google Scholar 

  35. Gracie R, Oswald J, Belytschko T (2008) On a new extended finite element method for dislocations: core enrichment and nonlinear formulation. J Mech Phys Solids 56:200–214. doi:10.1016/j.jmps.2007.07.010

    Article  MathSciNet  MATH  Google Scholar 

  36. Legay A, Chessa J, Belytschko T (2006) An Eulerian–Lagrangian method for fluid-structure interaction based on level sets. Comput Method Appl Mech 195:2070–2087. doi:10.1016/j.cma.2005.02.025

    Article  MathSciNet  MATH  Google Scholar 

  37. Chen JS, Wu CT, Yoon S, You Y (2001) A stabilized conforming nodal integration for Galerkin mesh-free methods. Int J Numer Method Eng 50:435–466. doi:10.1002/1097-0207(20010120)50:2<435:AID-NME32>3.0.CO;2-A

    Google Scholar 

  38. Moës N, Cloirec M, Cartraud P, Remacle JF (2003) A computational approach to handle complex microstructure geometries. Comput Method Appl Mech 192:3163–3177. doi:10.1016/S0045-7825(03)00346-3

    Article  MATH  Google Scholar 

  39. Bordas SPA, Natarajan S (2010) On the approximation in the smoothed finite element method (SFEM). Int J Numer Method Eng 81:660–670. doi:10.1002/Nme.2713

    MathSciNet  MATH  Google Scholar 

  40. Dasgupta G (2003) Interpolants within convex polygons: wachspress shape functions. J Aerospace Eng 16:1–8. doi:10.1061/(Asce)0893-1321(2003)16:1(1)

    Google Scholar 

  41. Liu GR, Nguyen TT, Dai KY, Lam KY (2007) Theoretical aspects of the smoothed finite element method (SFEM). Int J Numer Method Eng 71:902–930. doi:10.1002/Nme.1968

    Article  MathSciNet  MATH  Google Scholar 

  42. Meyers MA, Chawla KK (2009) Mechanical behavior of materials, 2nd edn. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  43. Fahrmann M, Fratzl P, Paris O, Fahrmann E, Johnson WC (1995) Influence of coherency stress on microstructural evolution in Model Ni–Al–Mo alloys. Acta Metall Mater 43:1007–1022. doi:10.1016/0956-7151(94)00337-H

    Article  Google Scholar 

  44. Maheshwari A, Ardell AJ (1993) Morphological evolution of coherent misfitting precipitates in anisotropic elastic media. Phys Rev Lett 70:2305–2308. doi:10.1103/PhysRevLett.70.2305

    Article  Google Scholar 

  45. Kaganova IM, Roitburd AL (1988) Equilibrium between elastically interacting phases. Soviet Physics: JETP 67:1173–1183

    Google Scholar 

  46. Johnson WC, Cahn JW (1984) Elastically induced shape bifurcations of inclusions. Acta Metall 32:1925–1933. doi:10.1016/0001-6160(84)90174-3

    Google Scholar 

  47. Johnson WC, Berkenpas MB, Laughlin DE (1988) Precipitate shape transitions during coarsening under uniaxial-stress. Acta Metall 36:3149–3162. doi:10.1016/0001-6160(88)90051-X

    Google Scholar 

  48. Schmidt I, Mueller R, Gross D (1998) The effect of elastic inhomogeneity on equilibrium and stability of a two particle morphology. Mech Mater 30:181–196. doi:10.1016/S0167-6636(98)00047-7

    Article  Google Scholar 

  49. Mueller R, Eckert S, Gross D (2000) 3D equilibrium shapes of periodically arranged anisotropic precipitates with elastic misfit. Arch Appl Mech 52:663–683

    MATH  Google Scholar 

  50. Voorhees PW, Mcfadden GB, Johnson WC (1992) On the morphological development of second-phase particles in elastically-stressed solids. Acta Metall Mater 40:2979–2992. doi:10.1016/0956-7151(92)90462-N

    Article  Google Scholar 

  51. Kolling S, Mueller R, Gross D (2003) The influence of elastic constants on the shape of an inclusion. Int J Solids Struct 40:4399–4416. doi:10.1016/S0020-7683(03)00183-5

    Article  MATH  Google Scholar 

  52. Sethian JA (1999) Fast marching methods. SIAM Rev 41:199–235. doi:10.1137/S0036144598347059

    Article  MathSciNet  MATH  Google Scholar 

  53. Osher S, Fedkiw RP (2003) Level set methods and dynamic implicit surfaces. Springer, New York

    MATH  Google Scholar 

  54. Schmidt I, Gross D (1997) The equilibrium shape of an elastically inhomogeneous inclusion. J Mech Phys Solids 45:1521–1549. doi:10.1016/S0022-5096(97)00011-2

    Article  MathSciNet  MATH  Google Scholar 

  55. Su CH, Voorhees PW (1996) The dynamics of precipitate evolution in elastically stressed solids. 1. Inverse coarsening. Acta Mater 44:1987–1999. doi:10.1016/1359-6454(95)00284-7

    Article  Google Scholar 

  56. Thompson ME, Su CS, Voorhees PW (1994) The equilibrium shape of a misfitting precipitate. Acta Metall Mater 42:2107–2122. doi:10.1016/0956-7151(94)90036-1

    Article  Google Scholar 

  57. Jog CS, Sankarasubramanian R, Abinandanan TA (2000) Symmetry-breaking transitions in equilibrium shapes of coherent precipitates. J Mech Phys Solids 48:2363–2389. doi:10.1016/S0022-5096(00)00005-3

    Article  MathSciNet  MATH  Google Scholar 

  58. Kerfriden P, Gosselet P, Adhikari S, Bordas SPA (2011) Bridging proper orthogonal decomposition methods and augmented Newton–Krylov algorithms: an adaptive model order reduction for highly nonlinear mechanical problems. Comput Method Appl Mech 200:850–866. doi:10.1016/j.cma.2010.10.009

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

XZ and JQ acknowledge the partial support by NSF through CMMI-1200075. SPAB acknowledges partial support from the European Research Council Starting Independent Research Grant (ERC Stg No. 279578) and EPSRC’s grants EP/G042705/1 and EP/I006761/1.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Northwestern University, Evanston, IL, 60208, USA

    Xujun Zhao & Jianmin Qu

  2. Department of Civil and Environmental Engineering, Northwestern University, Evanston, IL, 60208, USA

    Jianmin Qu

  3. Cardiff School of Engineering, Institute of Mechanics and Advanced Materials Theoretical, Applied and Computational Mechanics, Cardiff University, The Parade, Cardiff, Wales, CF24 3AA, UK

    Stéphane P. A. Bordas

Authors
  1. Xujun Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Stéphane P. A. Bordas
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jianmin Qu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Stéphane P. A. Bordas or Jianmin Qu.

Additional information

Stéphane P. A. Bordas’s ORCID ID is 0000-0001-7622-2193.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhao, X., Bordas, S.P.A. & Qu, J. A hybrid smoothed extended finite element/level set method for modeling equilibrium shapes of nano-inhomogeneities. Comput Mech 52, 1417–1428 (2013). https://doi.org/10.1007/s00466-013-0884-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-013-0884-1

Keywords

Search

Navigation