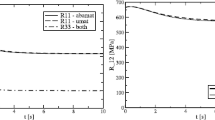Abstract
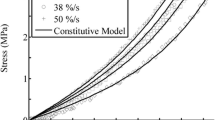
Creep and stress relaxation are known to be interrelated in linearly viscoelastic materials by an exact analytical expression. In this article, analytical interrelations are derived for nonlinearly viscoelastic materials which obey a single integral nonlinear superposition constitutive equation. The kernel is not assumed to be separable as a product of strain and time dependent parts. Superposition is fully taken into account within the single integral formulation used. Specific formulations based on power law time dependence and truncated expansions are developed. These are appropriate for weak stress and strain dependence. The interrelated constitutive formulation is applied to ligaments, in which stiffness increases with strain, stress relaxation proceeds faster than creep, and rate of creep is a function of stress and rate of relaxation is a function of strain. An interrelation was also constructed for a commercial die-cast aluminum alloy currently used in small engine applications.





Similar content being viewed by others
References
Andrews LC (1985) Special functions for engineers and applied mathematicians. Macmillan, New York
Artin E (1964) The Gamma function—Translated by Michael Butler. Holt, Rinehart and Winston, New York
Arutyunyan NKh (1966) Some problems in the theory of creep. Pergamon, Oxford, UK
Ashby MF, Jones DRH (1980) Engineering materials. Pergamon, Oxford
Findley WN, Lai JS, Onaran K (1976) Creep and relaxation of nonlinear viscoelastic materials. North Holland, Amsterdam
Fung YC (1972) Stress strain history relations of soft tissues in simple elongation in biomechanics, its foundations and objectives. Fung YC, Perrone N, Anliker M (eds) Prentice Hall, Englewood Cliffs, NJ
Gross B (1968) Mathematical structure of the theories of viscoelasticity. Hermann, Paris
Guth, Wack and Anthony (1946) Significance of the equation of state for rubber. J Appl Phys 17:347
Johnson GA, Livesay GA, Woo SL-Y, Rajagopal KR (1996) A single integral finite strain viscoelastic model of ligaments and tendons. J Biomech Eng 118:221–226
Kastelic J, Galeski A, Baer E (1978) The multicomposite structure of tendon. Conn Tissue Res 6:11–23
Kraus H (1980) Creep analysis. Wiley, New York
Kwon Y, Kwang SC (2001) Time-strain nonseparability in viscoelastic constitutive equations. J. Rheol 45(6):1441–1451
Lai JSY, Findley WN (1968) Prediction of uniaxial stress relaxation from creep of nonlinear viscoelastic material. Transactions of Society of Rheology 12(2):243–257
Lakes RS, Vanderby R (1999) Interrelation of creep and relaxation: a modelling approach for ligaments. ASME J Biomech Eng 121(6):612–615
Pioletti DP, Rakotomanana LR (2000) On the independence of time and strain effects in the stress relaxation of ligaments and tendons. J Biomech 33:1729–1732
Pioletti DP, Rakotomanana LR, Benvenuti JF, Leyvraz PF (1998) Viscoelastic constitutive law in large deformations: application to human knee ligaments and tendons. J Biomech Eng 31(8):753–757
Popov EP (1947) Correlation of tension creep tests with relaxation tests. J Appl Mech 14:135–142
Provenzano P, Lakes RS, Keenan T, Vanderby R (2001) Non-linear ligament viscoelasticity. Ann Biomed Eng 28:908–914
Schapery RA (1969) On the characterization of nonlinear viscoelastic materials. Polym Eng Sci 9(4):295–310
Thornton GM, Oliynyk A, Frank CB, Shrive NG (1997) Ligament creep cannot be predicted from stress relaxation at low stress: a biomechanical study of rabbit medial collateral ligament. J Orthop Res 15:652–656
Touati D, Cederbaum G (1997) On the prediction of stress relaxation from known creep of nonlinear materials. J Eng Mater Technol 119:121–124
Viidik A (1968) A rheological model for uncalcified parallel-fibered collagenous tissue. J Biomech 1:3–11
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
From the proof given below in Appendix B we get
However there is a standard identity (Artin 1964) for the product of gamma functions on the right hand side in Eq. (A1) which is given as
So Eq. (A1)can therefore be written as
Appendix B
The method used to solve the integral of type used in the formulation is as follows:
Rewriting Eq. (B1) in a different form we get
So when τ=0, u=0and when τ=t, u=1
Substituting the above result in Eq. (B2), we get
The integral part in Eq. (B3) is nothing but a Beta function (Andrews 1985), the definition of which is given as
So the final result can be written as
Rights and permissions
About this article
Cite this article
Oza, A., Vanderby, R. & Lakes, R.S. Interrelation of creep and relaxation for nonlinearly viscoelastic materials: application to ligament and metal. Rheol Acta 42, 557–568 (2003). https://doi.org/10.1007/s00397-003-0312-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00397-003-0312-0