Skin friction topology in a region enclosed by penetrable boundary

Abstract

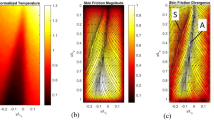
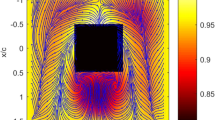
High-resolution skin friction fields in separated flows on a low-aspect-ratio rectangular wing are obtained by using quantitative global skin friction diagnostics based on surface luminescent oil visualizations. The topological features like the isolated singular points and the boundary switch points in regions enclosed by penetrable boundaries are identified. The conservation law given by the Poincare–Bendixson index formula for the numbers of the isolated singular points and the boundary switch points is used as a general approach to analyze the topological structure of a skin friction field in a singly connected region enclosed by a penetrable boundary in the separated flows.

Appendix

1.1 Simple derivation of the Poincare–Bendixson index formula

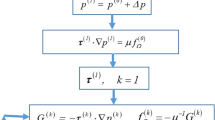
Consider a vector field on a surface in a region enclosed by a penetrable boundary across which vectors can move freely inward and outward. The relationship between the isolated singular points enclosed by the boundary and the inflow and outflow across the boundary exists as a topological constraint. In fact, this constraint was discussed by Hartman (1964) and Izydorek et al. (1996) in the framework of the Poincare–Bendixson theory. Furthermore, de Leeuw and van Liere (1999) gave a useful form of the constraint on the numbers of the isolated singular points and the positive and negative switch points on the boundary. Here, a more applicable form of the constraint for the flow topology analysis is given as a conservation law between the numbers of the isolated singular points and the switch points in a singly connected region enclosed a penetrable boundary on a surface. It is noted that the following result cannot be considered as a new theorem since it is a direct consequence of the previous works. The intent of this Appendix is to provide an exposition of the Poincare–Bendixson index formula for fluid dynamicists.

Consider an open set Ω ⊂ R ² bounded by a closed boundary $\partial \Upomega$ and define τ is a smooth 2D vector field on Ω. It is assumed that there are a finite number of the isolated singular points $x_{1} , \ldots ,x_{n} \in \Upomega$. The index of τ at x _k is denoted by I _k  = w(C _k ) that is defined as the winding number on a small circle C _k around x _k (Kinsey 1991). We denote B ⁺ as the segment of the boundary where τ moves inward across $\partial \Upomega$ and B ⁻ as the segment where τ moves outward across $\partial \Upomega$. If there exists a point $Z \in \partial \Upomega$ at which $B^{ + }$ and B ⁻ are divided, this point is called a switch point. There are two types of switch points. If τ in a sufficiently small neighborhood of $Z \in \partial \Upomega$ moves inward first and then outward across $\partial \Upomega$, this switch point is negative, which is denoted by Z ⁻. Otherwise, a switch point is positive, which is denoted by Z ⁺, if τ moves outward first and then inward across $\partial \Upomega$ in its neighborhood. The negative and positive switch points on a boundary are illustrated in Fig. 14. In fact, the positive and negative switch points are also called the internal and external tangent points termed by Hartman (1964) and Izydorek et al. (1996).

Fig. 14

Boundary switch points, (a) negative one and (b) positive one

Since $\Upomega \subset R^{2}$ is homeomorphic to a unit disk $D = \left\{ {\,\left. {\,x \in R^{2} } \right|\,\;|x|\; < \;1\,} \right\}$, the closed boundary $\partial \Upomega$ is topologically equivalent to a unit circle $C = \partial D$. The Poincare index theorem for a disk indicates $w(C) = \sum\nolimits_{k} {I_{k} }$, where $w(C)$ is the winding number of τ on C that is also the index of C (Kinsey 1991). Further, the winding number w(C) is given by $w(C) = {{1 + (e - h)} \mathord{\left/ {\vphantom {{1 + (e - h)} 2}} \right. \kern-\nulldelimiterspace} 2}$ according to the Poincare–Bendixson theorem, where e is the number of the elliptical sectors and h is the number of the hyperbolic sectors of τ (Chow and Hale 1982, Firby and Gardiner 2001). As illustrated in Fig. 15, an elliptical sector and a hyperbolic sector correspond to a positive switch point and a negative switch point, respectively. In other words, e is equal to the number of the positive switch points and h the number of the negative switch points. Therefore, the relation between the indices of the singular points in Ω and the number of the switch points on $\partial \Upomega$ is

$$ \sum\limits_{k} {\,I_{k} } = 1 + \frac{1}{2}\;\left( {\sum\limits_{k} {\,Z_{k}^{ + } } - \sum\limits_{k} {\,Z_{k}^{ - } } } \right) . $$

(2)

Since Eq. (2) is a direct consequence of the Poincare index theorem for a disk and the Poincare–Bendixson theorem, it is simply referred to as the Poincare–Bendixson index formula.

Fig. 15

Sectors in the unit disk, where H, E and P denote the hyperbolic, elliptical and parabolic sectors, respectively