Linear mode-mixing of phonons with trapped ions

Abstract

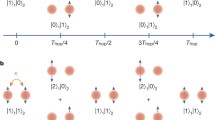
We propose a method to manipulate the normal modes in a chain of trapped ions using only two lasers. Linear chains of trapped ions have proven experimentally to be highly controllable quantum systems with a variety of refined techniques for preparation, evolution, and readout; however, typically for quantum information processing applications people have been interested in using the internal levels of the ions as the computational basis. We analyze the case where the motional degrees of freedom of the ions are the quantum system of interest, and where the internal levels are leveraged to facilitate interactions. In particular, we focus on an analysis of mode-mixing of phonons in different normal modes to mimic the quantum optical equivalent of a beam splitter.

Appendices

Appendix 1: Effective Hamiltonian terms

We label the internal state of the $\ell$-th ion by the two levels $|1\rangle \langle 1|_\ell$ and $|2\rangle \langle 2|_\ell$ and define ${\hat{\sigma }}_3^{(\ell )}=|2\rangle \langle 2|_\ell -|1\rangle \langle 1|_\ell$ as the usual atomic inversion operator. For compactness, we also define $\varSigma _{ab}=(-1)^a\nu _r+(-1)^b\nu _s-\Delta _1+\Delta _2$. Solving for the terms in the interaction Hamiltonian, we find the following; note that ${\hat{{\mathcal {H}}}}^{(\ell )}_{mn}={\hat{{\mathcal {H}}}}^{(\ell )\dagger }_{nm}$.

$$\begin{aligned} {\hat{{\mathcal {H}}}}_{11}^{(\ell )}&=\hbar |G_1|^2\frac{{\hat{a}}_r^\dagger {\hat{a}}_r {\hat{\sigma }}_3^{(\ell )} - |1\rangle \langle 1|_\ell }{2M\nu _r(\nu _r-\Delta _1)}\nonumber \\ {\hat{{\mathcal {H}}}}_{22}^{(\ell )}&=-\hbar |G_1|^2\frac{{\hat{a}}_r^\dagger {\hat{a}}_r {\hat{\sigma }}_3^{(\ell )} + |2\rangle \langle 2|_\ell }{2M\nu _r(\nu _r+\Delta _1)}\nonumber \\ {\hat{{\mathcal {H}}}}_{33}^{(\ell )}&=\hbar |G_2|^2\frac{{\hat{a}}_s^\dagger {\hat{a}}_s {\hat{\sigma }}_3^{(\ell )} - |1\rangle \langle 1|_\ell }{2M\nu _s(\nu _s-\Delta _2)}\nonumber \\ {\hat{{\mathcal {H}}}}_{44}^{(\ell )}&=-\hbar |G_2|^2\frac{{\hat{a}}_s^\dagger {\hat{a}}_s {\hat{\sigma }}_3^{(\ell )} + |2\rangle \langle 2|_\ell }{2M\nu _s(\nu _s+\Delta _2)}\nonumber \\ {\hat{{\mathcal {H}}}}_{21}^{(\ell )}&=\hbar |G_1|^2\frac{\Delta _1({\hat{a}}_r^\dagger )^2{\hat{\sigma }}_3^{(\ell )}}{2M(\nu _r^3-\nu _r\Delta _1^2)}e^{2i\nu _rt}\nonumber \\ {\hat{{\mathcal {H}}}}_{31}^{(\ell )}&=\hbar G_1^*G_2\frac{(\nu _r+\nu _s-\Delta _1-\Delta _2){\hat{a}}_r^\dagger {\hat{a}}_s {\hat{\sigma }}_3^{(\ell )}}{4M\sqrt{\nu _r\nu _s}(\nu _r-\Delta _1)(\nu _s-\Delta _2)}e^{it\varSigma _{01}}\nonumber \\ {\hat{{\mathcal {H}}}}_{41}^{(\ell )}&=-\hbar G_1^*G_2\frac{(\nu _r-\nu _s-\Delta _1-\Delta _2){\hat{a}}_r^\dagger {\hat{a}}_s^\dagger {\hat{\sigma }}_3^{(\ell )}}{4M\sqrt{\nu _r\nu _s}(\nu _r-\Delta _1)(\nu _s+\Delta _2)}e^{it\varSigma _{00}}\nonumber \\ {\hat{{\mathcal {H}}}}_{32}^{(\ell )}&=-\hbar G_1^*G_2\frac{(-\nu _r+\nu _s-\Delta _1-\Delta _2){\hat{a}}_r{\hat{a}}_s{\hat{\sigma }}_3^{(\ell )}}{4M\sqrt{\nu _r\nu _s}(\nu _r+\Delta _1)(\nu _s-\Delta _2)}e^{it\varSigma _{11}}\nonumber \\ {\hat{{\mathcal {H}}}}_{42}^{(\ell )}&=\hbar G_1^*G_2\frac{(-\nu _r-\nu _s-\Delta _1-\Delta _2){\hat{a}}_r{\hat{a}}_s^\dagger {\hat{\sigma }}_3^{(\ell )}}{4M\sqrt{\nu _r\nu _s}(\nu _r+\Delta _1)(\nu _s+\Delta _2)}e^{it\varSigma _{10}}\nonumber \\ {\hat{{\mathcal {H}}}}_{43}^{(\ell )}&=\hbar |G_2|^2\frac{\Delta _2({\hat{a}}_s^\dagger )^2{\hat{\sigma }}_3^{(\ell )}}{2M(\nu _s^3-\nu _s\Delta _2^2)}e^{2i\nu _st}. \end{aligned}$$

(19)

As one can see from the above expressions, our protocol relies on a second-order effect. One might worry that terms are missing as a result starting with a first-order Taylor expansion of the full Hamiltonian given in Eq. (18) and then finding effective second-order terms arising from time-ordering. We note that terms second-order in the Lamb–Dicke parameter ${\mathcal {O}}(\eta ^2)$ which would arise from further Taylor expansion would oscillate on the order of the detuning $\Delta$, and these can be safely neglected as the corrections they would impose would be ${\mathcal {O}}(\eta ^4)$.

Appendix 2: Beyond the Lamb–Dicke approximation

The appropriateness of the Lamb–Dicke approximation can be assessed by a more thorough treatment of our proposed method. The true interaction Hamiltonian is given as

$$\begin{aligned} {\hat{H}}_{\rm{int}}^{(\ell )}&=\frac{\hbar \varOmega }{2} {\hat{\sigma }}_+^{(\ell )} \exp \left\{ i\left[ \eta \left( {\hat{a}}_\ell e^{-i\nu t}+{\hat{a}}_\ell ^\dagger e^{i\nu t}\right) -t\Delta +\psi \right] \right\} \nonumber \\&\quad +h.c. \end{aligned}$$

(20)

Using an identity [32], we can express $\varOmega _{n^{\prime}n}=\varOmega \langle n^{\prime}|e^{i\eta (a+a^\dag )}|n\rangle$ as

$$\begin{aligned} \varOmega _{n^{\prime}n}&=\varOmega e^{-\eta ^2/2} \sqrt{\frac{n_<!}{n_>!}} \eta ^{|n^{\prime}-n|} L_{n_<}^{|n^{\prime}-n|}(\eta ^2), \end{aligned}$$

(21)

where $n_>$ ($n_<$) is the greater (lesser) of $n^{\prime}$ and n, and $L_n^\alpha$ is the generalized Laguerre polynomial

$$\begin{aligned} L_n^\alpha (x)=\sum _{m=0}^n(-1)^m\left( {\begin{array}{c}n+\alpha \\ n-m\end{array}}\right) \frac{x^m}{m!}. \end{aligned}$$

(22)

By noting that

$$\begin{array}{l} \Omega \langle {n^\prime }|\exp \left[ {i\eta \left( {\hat a{e^{ - i\nu t}} + {{\hat a}^\dag }{e^{i\nu t}}} \right)} \right]|n\rangle \\ = \Omega \langle {n^\prime }|{e^{i\nu {{\hat a}^\dag }\hat at}}\exp \left[ {i\eta \left( {\hat a + {{\hat a}^\dag }} \right)} \right]{e^{ - i\nu {{\hat a}^\dag }\hat at}}|n\rangle \\ = \Omega \langle {n^\prime }|\exp \left[ {i\eta \left( {\hat a + {{\hat a}^\dag }} \right)} \right]|n\rangle {e^{i\nu ({n^\prime } - n)t}}\\ = {\Omega _{n\prime n}}{e^{i\nu (n\prime - n)t}}, \end{array}$$

(23)

we can now write the Hamiltonian as

$$\begin{aligned} {\hat{H}}_{int}^{(\ell )}&=\frac{\hbar }{2} {\hat{\sigma }}_+^{(\ell )} \sum _{n^{\prime},n} \varOmega _{n^{\prime}n} |n^{\prime}\rangle \langle n| e^{-i(\Delta t-\psi )}e^{i\nu (n^{\prime}-n)t}+h.c. \end{aligned}$$

(24)

where we denote $\varGamma =n^{\prime}-n$ to emphasize that terms with fixed $\varGamma$ have the same frequency. Motivated by this, we can express the interaction as

$$\begin{aligned} {\hat{H}}_{\rm{int}}^{(\ell )}&=\frac{\hbar }{2} {\hat{\sigma }}_+^{(\ell )} \sum _{n,\varGamma } \varOmega _{n+\varGamma ,n} |n+\varGamma \rangle \langle n| e^{-i(\Delta t-\psi )}e^{i\nu \varGamma t}+h.c.\nonumber \\&=\sum _\varGamma {\hat{h}}_\varGamma e^{-i(\Delta -\nu \varGamma )t}+h.c. \end{aligned}$$

(25)

where

$$\begin{aligned} {\hat{h}}_\varGamma&=\frac{\hbar }{2} e^{i\phi } {\hat{\sigma }}_+^{(\ell )} \sum _n \varOmega _{n+\varGamma ,n}|n+\varGamma \rangle \langle n|. \end{aligned}$$

(26)

Provided the detuning $\Delta$ dominates this frequency over some appropriate range of $\varGamma$, such as if we had an upper bound on the number of phonons, then we can again appeal to the effective Hamiltonian approach. We can then compare these results to the results obtained in the Lamb–Dicke approximation.

For example, we compare the term containing $\eta {\hat{\sigma }}_+^{(\ell )}{\hat{a}}$ obtained in the Lamb–Dicke approximation to the corresponding term in Eq. (26). The former will have the matrix element $\eta \langle n^{\prime}|{\hat{a}} |n\rangle =\eta \sqrt{n}\delta _{n^{\prime},n-1}$ whereas the latter will have

$$\begin{aligned} \langle n^{\prime}|\left( \sum _m \varOmega _{m+\varGamma ,m}|m+\varGamma \rangle \langle m|\right) |n\rangle&=\varOmega _{n+\varGamma ,n}\delta _{n^{\prime},n+\varGamma } \end{aligned}$$

(27)

For the case of $\varGamma =-1$ we find that $\lim _{\eta \rightarrow 0}\varOmega _{n-1,n}\approx \eta \sqrt{n}$ as desired and all other transitions are suppressed by a factor of $\eta ^{|\varGamma |}$. Deviations from the first-order approximation can then be characterized by the how these matrix elements differ from the creation and annihilation operators assumed in the more simple treatment.

One can account for the transverse modes by adding additional terms to the exponential in Eq. (20), and these terms will give rise to similar terms ${\hat{h}}_\varGamma$ in the effective Hamiltonian picture, i.e., phase shifts, beam splitters, and squeezing operations. As presented in Sect. 5, these motional modes can be expressed in terms of the normal modes of the chain.