A mathematical model of the coupled mechanisms of cell adhesion, contraction and spreading

Abstract

Recent research has shown that cell spreading is highly dependent on the contractility of its cytoskeleton and the mechanical properties of the environment it is located in. The dynamics of such process is critical for the development of tissue engineering strategy but is also a key player in wound contraction, tissue maintenance and angiogenesis. To better understand the underlying physics of such phenomena, the paper describes a mathematical formulation of cell spreading and contraction that couples the processes of stress fiber formation, protrusion growth through actin polymerization at the cell edge and dynamics of cross-membrane protein (integrins) enabling cell-substrate attachment. The evolving cell’s cytoskeleton is modeled as a mixture of fluid, proteins and filaments that can exchange mass and generate contraction. In particular, besides self-assembling into stress fibers, actin monomers able to polymerize into an actin meshwork at the cell’s boundary in order to push the membrane forward and generate protrusion. These processes are possible via the development of cell-substrate attachment complexes that arise from the mechano-sensitive equilibrium of membrane proteins, known as integrins. After deriving the governing equation driving the dynamics of cell evolution and spreading, we introduce a numerical solution based on the extended finite element method, combined with a level set formulation. Numerical simulations show that the proposed model is able to capture the dependency of cell spreading and contraction on substrate stiffness and chemistry. The very good agreement between model predictions and experimental observations suggests that mechanics plays a strong role into the coupled mechanisms of contraction, adhesion and spreading of adherent cells.

Appendix: A

1.1 A.1 Plane-stress conditions elasticity equations for cell

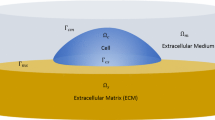
In this paper, it is assumed that the cell’s geometry can be described as a very thin plate such that two-dimensional plane-stress conditions can be applied. This implies that the total stress $\mathbf T$ verifies $T_{xz}=T_{yz}=0,T_{zz}=0$. Since stress fibers do not exert forces in the z-direction, the last equation can be written $T^{c}_{zz} - p=0$, where $p$ is the cytosol pressure. Writing the three-dimensional stress-strain relation for the actin filament network as:

$$\begin{aligned} \begin{bmatrix} T^c_{xx}\\ T^c_{yy}\\ T^c_{zz}\\ T^c_{yz}\\ T^c_{xz}\\ T^c_{xy} \end{bmatrix}&= \begin{bmatrix} 2\mu +\lambda&\quad \lambda&\quad \lambda&\quad 0&\quad 0&\quad 0\\ \lambda&\quad 2\mu +\lambda&\quad \lambda&\quad 0&\quad 0&\quad 0\\ \lambda&\quad \lambda&\quad 2\mu +\lambda&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad \mu&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad \mu&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad \mu \end{bmatrix} \begin{bmatrix} \varepsilon _{xx}\\ \varepsilon _{yy}\\ \varepsilon _{zz}\\ 2\varepsilon _{yz}\\ 2\varepsilon _{xz}\\ 2\varepsilon _{xy} \end{bmatrix}, \end{aligned}$$

(70)

and enforcing the fact that $T^c_{zz}=p$, we obtain the following expression for $\varepsilon _{zz}$:

$$\begin{aligned} \varepsilon _{zz}=\frac{1}{1-\nu }\left[ \frac{p}{E}(1+\nu )(1-2\nu )-\nu (\varepsilon _{xx}+\varepsilon _{yy}) \right] \end{aligned}$$

(71)

where $E$ and $\nu$ are the Young’s modulus and Poisson’s ratio of the actin filament network. Their relationship with Lame’s constants appearing in (70) is given below:

$$\begin{aligned} E=\frac{\mu ^{\prime }(3\lambda +2\mu ^{\prime })}{\lambda +\mu ^{\prime }};\quad {\text{ and}}\quad \nu =\frac{\lambda }{2(\lambda +\mu ^{\prime })} \end{aligned}$$

(72)

We now wish to express the divergence $\nabla \cdot \mathbf{v}^c$ of the velocity field $\mathbf{v}^c$ for substitution in the equations of mass balance (4–6). For a three dimensional problem, the divergence reads $\nabla \cdot \mathbf{v}^c={\dot{\varepsilon }}_{xx}+{\dot{\varepsilon }}_{yy} +{\dot{\varepsilon }}_{zz}$ where a superimposed dot is used to denote a time derivative. Using the fact that:

$$\begin{aligned} {\dot{\varepsilon }}_{zz}=\frac{1}{1-\nu }\left[ \frac{\dot{p}}{E}(1+\nu )(1-2\nu )-\nu ({\dot{\varepsilon }}_{xx} +{\dot{\varepsilon }}_{yy}) \right] \end{aligned}$$

(73)

from (71), we can rewrite:

$$\begin{aligned} \nabla \cdot \mathbf{v}^c=\alpha ~\nabla ^{(2)}\cdot \mathbf{v}+\beta ~ {\dot{p}} \end{aligned}$$

(74)

where $\nabla ^{(2)}\cdot \mathbf{v}=\partial v_x/\partial x+ \partial v_y/\partial y={\dot{\varepsilon }}_{xx}+ {\dot{\varepsilon }}_{yy}$ represents the divergence of the velocity $\mathbf{v}$ in the two-dimensional plane $xy$ while constants $\alpha$ and $\beta$ can be found to be:

$$\begin{aligned} \alpha =\frac{1-2\nu }{1-\nu };\quad {\text{ and}}\quad \beta =\frac{(1+\nu )(1-2\nu )}{E(1-\nu )} \end{aligned}$$

(75)

In the particular case of axisymmetric conditions, (74) becomes:

$$\begin{aligned} \nabla \cdot \mathbf{v}^c=\alpha \left( \frac{\partial v^c}{\partial r}+ \frac{v^c}{r}\right) +\beta ~{\dot{p}} \end{aligned}$$

(76)

This result is used to obtain Eqs. (7) and (8) in the present study.

1.2 A.2 Stiffness and damping matrices

It can be shown, through a standard finite-element procedure, that the force vector, damping matrix and stiffness matrix appearing in Eq. (63) take the following form:

$$\begin{aligned} \mathbf{F}= {\fancyscript{A}}_{e=1}^{nel}\mathbf{F}^{e}\quad \mathbf{K}= {\fancyscript{A}}_{e=1}^{nel} \mathbf{K}^{e}\quad {\text{ and}}\quad \mathbf{C}={\fancyscript{A}}_{e=1}^{nel} \mathbf{C}^{e}. \end{aligned}$$

(77)

where the superscript $e$ denotes quantities associated with individual finite element $e$ and the symbol ${\fancyscript{A}}$ denotes the assembly operator. The final force vector, damping matrix, and stiffness matrix finally take the forms:

$$\begin{aligned} \mathbf{F}&= \begin{bmatrix} \mathbf{F}^{u^s}, \mathbf{F}^{u^c}, \mathbf{F}^f, \mathbf{F}^m, \mathbf{F}^c, \mathbf{F}^{SF,r}, \mathbf{F}^{SF,\theta }, \mathbf{F}^L, \mathbf{F}^H \end{bmatrix}^T, \end{aligned}$$

(78)

$$\begin{aligned} \mathbf{C}&= \begin{bmatrix} 0&0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0&0\\ 0&\mathbf{C}^{fu}&\mathbf{C}^{ff}&\mathbf{C}^{fm}&\mathbf{C}^{fc}&\mathbf{C}^{fr}&\mathbf{C}^{f\theta }&0&0\\ 0&\mathbf{C}^{mu}&\mathbf{C}^{mf}&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0&0\\ 0&\mathbf{C}^{Lu}&0&0&0&0&0&\mathbf{C}^{LL}&\mathbf{C}^{LH}\\ 0&0&0&0&0&0&0&0&0 \end{bmatrix} \end{aligned}$$

(79)

and

$$\begin{aligned} \mathbf{K}= \begin{bmatrix} \mathbf{K}^{ss}&\mathbf{K}^{su}&0&0&0&0&0&0&\mathbf{K}^{sH}\\ \mathbf{K}^{us}&\mathbf{K}^{uu}&\mathbf{K}^{uf}&0&0&\mathbf{K}^{ur}&\mathbf{K}^{u\theta }&0&\mathbf{K}^{uH}\\ 0&0&\mathbf{K}^{ff}&0&0&0&0&0&0\\ 0&0&\mathbf{K}^{mf}&\mathbf{K}^{mm}&\mathbf{K}^{mc}&\mathbf{K}^{mr}&\mathbf{K}^{m\theta }&0&0\\ 0&0&0&\mathbf{K}^{cm}&\mathbf{K}^{cc}&0&0&0&0\\ 0&\mathbf{K}^{ru}&0&\mathbf{K}^{rm}&0&\mathbf{K}^{rr}&0&0&0\\ 0&\mathbf{K}^{\theta u}&0&\mathbf{K}^{\theta m}&0&0&\mathbf{K}^{\theta \theta }&0&0\\ 0&0&0&0&0&0&0&\mathbf{K}^{LL}&0\\ \mathbf{K}^{Hs}&\mathbf{K}^{Hu}&0&0&0&0&0&\mathbf{K}^{HL}&\mathbf{K}^{HH} \end{bmatrix} \end{aligned}$$

(80)

where the superscripts $ij$ is used to designate a matrix representing the interactions between component $i$ and component $j$.