Optimality versus variability: effect of fatigue in multi-finger redundant tasks

Abstract

We used two methods to address two aspects of multi-finger synergies and their changes after fatigue of the index finger. Analytical inverse optimization (ANIO) was used to identify cost functions and corresponding spaces of optimal solutions over a broad range of task parameters. Analysis within the uncontrolled manifold (UCM) hypothesis was used to quantify co-variation of finger forces across repetitive trials that helped reduce variability of (stabilized) performance variables produced by all the fingers together. Subjects produced steady-state levels of total force and moment of force simultaneously as accurately as possible by pressing with the four fingers of the right hand. Both before and during fatigue, the subjects performed single trials for many force–moment combinations covering a broad range; the data were used for the ANIO analysis. Multiple trials were performed at two force–moment combinations; these data were used for analysis within the UCM hypothesis. Fatigue was induced by 1-min maximal voluntary contraction exercise by the index finger. Principal component (PC) analysis showed that the first two PCs explained over 90% of the total variance both before and during fatigue. Hence, experimental observations formed a plane in the four-dimensional finger force space both before and during fatigue conditions. Based on this finding, quadratic cost functions with linear terms were estimated from the experimental data. The dihedral angle between the plane of optimal solutions and the plane of experimental observations (D _ANGLE) was very small (a few degrees); it increased during fatigue. There was an increase in fatigue of the coefficient at the quadratic term for the index finger force balanced by a drop in the coefficients for the ring and middle fingers. Within each finger pair (index–middle and ring–little), the contribution of the “central” fingers to moment production increased during fatigue. An index of antagonist moment production dropped with fatigue. Fatigue led to higher co-variation indices during pronation tasks (index finger is an agonist) but opposite effects during supination tasks. The results suggest that adaptive changes in co-variation indices that help stabilize performance may depend on the role of the fatigued element, agonist or antagonist.

Appendices

Appendix 1

Analytical inverse optimization (ANIO) approach

The optimization problem in the current study was defined as

$$\begin{array}{ll} {\text{Min}}&\quad J = \sum\limits_{i = 1}^{4} {g_{i} (F_{i} )}\\{\text{Subject} \text{ to}}&\quad F_{\rm I} + F_{\rm M} + F_{\rm R} + F_{\rm L} = a \cdot {\text{MVC}}_{\text{IMRL}}\\&d_{\rm I} \cdot F_{\rm I} + d_{\rm M} \cdot F_{\rm M} + d_{\rm R} \cdot F_{\rm R} + d_{\rm L} \cdot F_{\rm L} = b \cdot 0.07 \cdot d_{\rm I} \cdot {\text{MVC}}_{\rm I}\end{array} $$

(10)

The two linear constraints are expressed as

$$\begin{array}{ll} {\text{CF}}^{T} = B \\& F = \left[ {\begin{array}{*{20}c} {F_{\rm I} } & {F_{\rm M} } & {F_{\rm R} } & {F_{\rm L} } \\ \end{array} } \right] \\& C = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 \\ {d_{\rm I} } & {d_{\rm M} } & {d_{\rm R} } & {d_{\rm L} } \\ \end{array} } \right] \end{array}$$

(11)

$$ B = \left[ {\begin{array}{*{20}c} {F_{\text{TOT}} } \\ {M_{\text{TOT}} } \\ \end{array} } \right]. $$

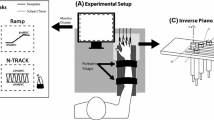
The task involved two constraints (F _TOT and M _TOT values) and four elemental variables (finger forces). Thus, the solutions of this undetermined system were expected to be confined to a two-dimensional surface in the four-dimensional force space. Planarity of this surface was checked using the PCA. The following computational procedure explains how the optimization cost function is obtained.

First, we identify whether the optimization problem is splittable or not by observing the (4 × 4) matrix:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} = I - C^{T} (CC^{T} )^{ - 1} C $$

(12)

Second, we check whether the experimental data actually lie on a hyperplane (and not for instance on a curved hypersurface) and then define the observed hyperplane mathematically as

$$ A \cdot F^{T} = b $$

(13)

where A is a 2 × 4 matrix composed of the transposed vectors of the two lesser principal components obtained from the PCA from the finger force data. A large percentage of the total variance explained by the two first principal components was considered an indicator that the data lie on a hyperplane. However, the data points were not perfectly confined to a plane due to the variability of performance and instrumental noise. Also, the plane computed from Eq. 13 is affected by experimental errors.

Third, we compare the experimentally determined hyperplane to the theoretical plane derived from the uniqueness theorem. The experimental data must be fitted by the following equation:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} f^{\prime } (F) = 0 , $$

(14)

where $f^{\prime } (F) = (f_{1}^{\prime } (F_{\rm I} ),f_{2}^{\prime } (F_{\rm M} ),f_{3}^{\prime } (F_{\rm R} ),f_{4}^{\prime } (F_{\rm L} ))^{T}$ f _i are arbitrary continuously differentiable functions. At the second step, the data are discovered to lie on the plane and hence the function $f_{i}^{\prime } ( \cdot )$ is linear:

$$ f_{i}^{\prime } (F_{i} ) = k_{i} F_{i} + w_{i} $$

(15)

where i = {index (I), middle (M), ring (R), and little (L)}. Therefore,

$$ f_{i} (F_{i} ) = \frac{{k_{i} }}{2}(F_{i} )^{2} + w_{i} F_{i} . $$

(16)

The values of the coefficients of the second-order terms k _i can be determined by minimizing the dihedral angle between the two planes: the plane of optimal solutions $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} f^{\prime } (F) = 0$ and the plane of experimental observations (A · F ^T = 0). The values of the coefficients of the first-order terms w _i were found to correspond to a minimal vector length (w = (w _index, w _middle, w _ring, w _little)^T) bringing the theoretical and the experimental plane as close to each other as possible. Vector w satisfy the following equation:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} f^{\prime } (F) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} (KF_{i} + w) $$

(17)

where K = (k _I , k _M , k _R , k _L)^T and w = (w _I , w _M , w _R , w _L)^T.

Then, the functions g _i in Eq. 12 are the following:

$$ g_{i} (x_{i} ) = rf_{i} (F_{i} ) + q_{i} F_{i} + {\text{const}}_{i} $$

(18)

where r is a non-zero number, const _i can be any real number and q _i is any real number satisfying the equation $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} q = 0$ (Terekhov et al. 2010). Multiplication of the cost function by a constant value or adding a constant value to it does change the cost function essentially. Hence, we can arbitrarily assume that r = 1 and consti = 0. According to the uniqueness theorem, identification of the cost function can be performed only up to unknown linear terms that are parameterized by the values qi. We assume that qi = 0 in order to simplify gi(xi). It must be kept in mind, however, that the true cost function used by the CNS might have these terms.

Uniqueness theorem (for the mathematical proof see Terekhov et al. 2010)

The core of the ANIO approach is the theorem of uniqueness that specifies conditions for unique (with some restrictions) estimation of the objective functions. The main idea of the theorem of uniqueness is to find necessary conditions for the uniqueness of solutions in an inverse optimization problem. An optimization problem (i.e., direct optimization problem) with an additive objective function and linear constraints is defined as

$$ \begin{array}{*{20}c} {\text{Let}\,J:} & {R^{n} \to R^{1} } \\ {\text{Min:}} & {J(x) = g_{1} (x_{1} ) + g_{2} (x_{2} ) + \cdots + g_{n} (x_{n} )} \\ {{\text{Subject}}\,{\text{to:}}} & {{\text{CX}}^{T} = B} \\ \end{array} $$

(19)

where X = (x ₁, x ₂,…, x _n) ∈ R ⁿ, g _i is an unknown scalar differentiable function with g′(⋅) > 0. g _i came from the Lagrange minimum principle, which has a unique solution. On the contrary, the functions of g _i can be computed from the set of solutions X ^* (e.g., experimental data). This inverse procedure is called the inverse optimization problem. C is a k × n matrix and B is a k-dimension vector, k < n.

First, assume that the optimization problem (19) with k ≥ 2 is non-splittable. If the inverse optimization is splittable, the preliminary step is to split it until a non-splittable subproblem is acquired. If the functions g _i (x _i ) in problem (19) are twice continuously differentiable (i.e., twice continuously differentiable functions f _i ) and $f_{i}^{\prime }$ is not identically constant, complying $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} f^{\prime } (X) = 0$ for all X ∈ X ^*,

$$ f^{\prime } (X) = (f_{1}^{\prime } (x_{1} ), \ldots ,f_{n}^{\prime } (x_{n} ))^{T} $$

(20)

and

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} = I - C^{T} (CC^{T} )^{ - 1} C $$

(21)

then

$$ g_{i} (x_{i} ) = {rf}_{i} (x_{i} ) + q_{i} x_{i} + {\text{const}}_{i} $$

(22)

for every $x_{i} \in X_{i}^{*}$, where $X_{i}^{*}$ = {s| there is X ∈ X ^*: x _i  ∈ s} and X ^* is the set of the solutions for all B ∈ R ^k. The constants q _i satisfy the equation $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} q = 0$ where $q = (q_{1} , \ldots ,q_{n} )^{T}$. Primes designate derivatives.

If the experimental data correspond to solutions of an inverse optimization problem with additive objective function (g _i ) and linear constraints, equation $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} f^{\prime } (X) = 0$ (X ∈ X ^*) must be satisfied (i.e., the Lagrange principle). The uniqueness theorem provides sufficient condition (i.e., $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} f^{\prime } (X) = 0$) for solving the inverse optimization problem in a unique way up to linear terms.

Appendix 2

Uncontrolled manifold (UCM) analysis (see Latash et al. 2002; Scholz et al. 2002 for details)

For F _TOT, changes in the elemental variables (finger forces) sum up to produce a change in F _TOT:

$$ {\text{d}}F_{\text{TOT}} = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {{\text{d}}F_{\rm I} } & {{\text{d}}F_{\rm M} } & {{\text{d}}F_{\rm R} } & {{\text{d}}F_{\rm L} } \\ \end{array} } \right]^{T} $$

(23)

The UCM was defined as an orthogonal set of the vectors e _i in the space of the elemental forces that did not change the net normal force, i.e.,

$$ 0 = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 \\ \end{array} } \right]e_{i} $$

(24)

These directions were found by taking the null-space of the Jacobian of this transformation ([1 1 1 1] e _i ). The mean-free forces were then projected onto these directions and summed to produce

$$ f_{||} = \sum\limits_{i}^{n - p} {\left( {e_{i}^{T} \cdot {\text{d}}f} \right)e_{i} } , $$

(25)

where n = 4 is the number of degrees of freedom of the elemental variables and P = 1 is the number of degrees of freedom of the performance variable (F _TOT). The component of the de-meaned forces orthogonal to the null-space is given by

$$ f_{ \bot } = {\text{d}}f - f_{||} $$

(26)

The amount of variance per degree of freedom parallel to the UCM is

$$ V_{\text{UCM}} = \frac{{\sum {\left| {f_{||} } \right|^{2} } }}{{(n - p)N_{\text{trials}} }} $$

(27)

The amount of variance per degree of freedom orthogonal to the UCM is

$$ V_{\text{ORT}} = \frac{{\sum {\left| {f_{ \bot } } \right|^{2} } }}{{pN_{\text{trials}} }} $$

(28)

The normalized difference between these variances is quantified by a variable ΔV:

$$ \Updelta V = \frac{{V_{\text{UCM}} - V_{\text{ORT}} }}{{V_{\text{TOT}} }} $$

(29)

where V _TOT is the total variance, also quantified per degree of freedom. If ΔV is positive, V _UCM > V _ORT, caused by negative co-variation of the finger forces, which we interpret as evidence for a force-stabilizing synergy. In contrast, ΔV = 0 indicates independent variation of the finger forces, while ΔV < 0 indicates positive co-variation of the individual finger forces, which contributes to variance of F _TOT.

A similar procedure was used to compute the two variance components related to stabilization of M _TOT. The only difference was in using a different Jacobian corresponding to the lever arms of individual finger forces, [d _I d _M d _R d _L].

We also analyzed the data with respect to stabilization of both F _TOT and M _TOT simultaneously. In that case, the Jacobian was [1 1 1 1; d _I d _M d _R d _L]. The dimensionality of V _UCM for the analysis with respect to F _TOT and M _TOT separately is three (one constraint), while the dimensionality of V _UCM with respect to F _TOT and M _TOT simultaneously is two (two constraints).